噻虫嗪对活性污泥颗粒化影响的数学模型

张　明,苏馈足,鲍白翎

(合肥工业大学 土木与水利工程学院,安徽 合肥　230009)



噻虫嗪对活性污泥颗粒化影响的数学模型

张明,苏馈足,鲍白翎

(合肥工业大学 土木与水利工程学院,安徽 合肥230009)

摘要:文章在活性污泥1号模型(ASM1)的基础上加入抑制动力学模型,建立活性污泥颗粒化过程数学模型,模拟噻虫嗪(thiamethoxam,TMX)抑制和非抑制2种条件下,序批式反应器(sequencing batch reactor,SBR)中颗粒的生长及有机底物的去除、微生物总量的生长、TMX和溶解氧(dissolved oxygen,DO)在颗粒内部分布趋势以及自养菌、异养菌和TMX降解菌颗粒内部的空间分布。结果表明,TMX对自养菌和异养菌产生非竞争性抑制,同时对TMX降解菌产生底物抑制。DO对好氧颗粒内的微生物种群空间分布具有重要影响,DO在颗粒内部的传质深度为200～600 μm,所以基于氧气生长的自养菌和TMX降解菌在颗粒外层分布较多。不添加TMX时,异养菌均匀分布于整个颗粒;而添加TMX时,由于对异养菌的生长造成非竞争性抑制,故其空间分布变为内部多外层少。

关键词:好氧颗粒污泥;数学模型;抑制;噻虫嗪

好氧颗粒污泥(aerobic granular sludge,AGS)是在好氧条件下,通过微生物自凝聚作用形成的微生物聚合体。与传统活性污泥法相比,AGS具有含水率低、沉降性能好、处理效率高和可同步脱氮除磷等诸多优点,因此,近年来AGS已成为国内外专家学者研究的热点[1-2]。文献[3]研究了颗粒污泥在好氧和缺氧条件下的胞内储存过程机理,深入探讨了颗粒污泥中胞外聚合物和溶解性微生物产物的形成规律。文献[4-5]建立了基于序批式反应器(sequencing batch reactor,SBR)的颗粒污泥数学模型。文献[6]基于活性污泥1号模型(ASM1)建立了一个多元参数误差最小化的系统模型。文献[7]研究了活性污泥颗粒化过程中絮体与颗粒污泥的竞争作用。AGS已被较多地应用于高浓度有机废水[8]和有毒有害废水[9]等的处理中。随着农药在农业生产中扮演的角色越来越重要,其高渗透性和低土壤吸附性给地表和地下水带来的潜在污染问题也越发严重[10]。以噻虫嗪(thiamethoxam,TMX)为代表的农药废水处理成为亟待解决的问题。文献[11]研究了硝基氯苯生产废水中典型有机污染物及其生物可处理性,文献[12]在实验室条件下采用活性污泥工艺处理宣纸废水,但是由于实验的局限性,无法反映毒性物质的去除及抑制机理,因此本文建立基于ASM1的AGS抑制动力学模型来研究毒性难降解物质TMX对好氧颗粒污泥培养的影响及其降解效果。

1材料与方法

1.1模型的组分

本研究利用AQUASIM应用软件[13],建立基于ASM1[14]并加入抑制动力学的抑制模型,从而对SBR中AGS的生长情况进行模拟分析。本模型涉及8个组分,其中固体物质为自养菌、异养菌及TMX降解菌;溶解性物质为易降解有机底物、氨氮、硝态氮、溶解氧(dissolved oxygen,DO)以及TMX。

7个生物反应过程如下:① 异养菌利用易生物降解底物进行好氧生长;② 异养菌利用易生物降解底物进行缺氧生长;③ 异养菌的衰减;④ 自养菌的好氧生长;⑤ 自养菌的衰减;⑥ TMX降解菌降解的生长;⑦ TMX降解菌的衰减。

1.2物质的传质

本研究假定整个SBR反应器内的污泥由若干个性质相同的AGS组成,在单颗粒层次上建立AGS传质-反应模型。在颗粒与其表面的液相之间存在一个传质边界层,液相中的各溶解性物质(各种营养物质和DO)由该区域传质到颗粒内部。可溶解性物质可视为中性分子,其在边界层和颗粒污泥孔隙内液相的传递过程为分子扩散[15],由Fick第一扩散定律可知,传递过程可表示为:

(1)

其中,Jbound为溶解性物质i在传质边界层内的通量;Di为物质i在水中的分子扩散系数;Si为AGS内物质i的质量浓度;z为AGS模型模拟坐标系的纵坐标;ki为物质i的传递系数;SiL为物质i在液相主体的质量浓度;SiB为物质i在传质边界层接近固相的质量浓度。

反应器中氧气是在气液相之间进行扩散传质,氧的气液传质速率与气液表面氧的浓度差成正比,其比例系数即为氧的气液传质系数[16]aKL。在颗粒污泥表面,由气相传质到颗粒表面氧的量应等于扩散进入颗粒内部氧的量。其质量平衡方程为:

(2)

1.3颗粒的生长

在用AQUASIM软件模拟SBR反应器中AGS生长过程时,其颗粒增长速率[13]可表示为:

(3)

其中,LF为颗粒粒径;μL为颗粒增长速率。

1.4抑制动力学

本文模型中采用的Monod方程式仅适用于无毒性的基质,如有毒性物质存在,且达到一定浓度时,微生物的生长将受到抑制,其生长模式将有所不同。TMX作为一种毒性难降解物质,在降解过程中,其自身会对颗粒污泥中微生物的生长产生一定的非竞争性抑制作用,使得微生物的比生长速率减小,其动力学表达式[17]如下:

(4)

其中,μmax1为最大比生长速率;KI为抑制系数,取19.8 g/m3;SS为可降解有机底物的质量浓度;ST为TMX的质量浓度(抑制物的质量浓度);KS为异养菌的半饱和系数[14],取20 g/m3。

同时反应器中的TMX降解菌以TMX为单一底物进行生长会产生底物抑制,其动力学表达式[17]如下:

(5)

其中,μmax2为最大比生长速率;KST为TMX降解菌的半饱和系数,取5 g/m3;其他参数同上。

不同菌种模型矩阵见表1所列。表1中，XBA、XBH、XT分别为自养菌、异养菌、TMX降解菌的质量浓度；YA、YH、YT分别为自养菌、异养菌、TMX降解菌的产率系数。

表1　模型矩阵　g/m3

模型动力学的表达式如下。

自养菌在好氧生长过程的速率表达式为:

(6)

自养菌在衰减过程的速率表达式为:

(7)

异养菌在好氧生长过程的速率表达式为:

(8)

异养菌在缺氧生长过程的速率表达式为:

(9)

异养菌在衰减过程的速率表达式为:

(10)

TMX降解菌在好氧生长过程的速率表达式为:

(11)

TMX降解菌在衰减过程的速率表达式为:

bTXT

(12)

其中,bA、bH、bT分别为自养菌、异养菌、TMX降解菌的衰减系数[14,18],取值分别为0.2、0.62、0.62/d;KNH为自养菌的氨饱和系数[14],取1 g/m3;KNO为反硝化菌的硝酸盐饱和系数[14],取0.5 g/m3;KOA、KOH、KOT分别为自养菌、异养菌、TMX降解菌的氧饱和系数[14],取值分别为0.4、0.2、0.2 g/m3;μA、μH、μT分别为自养菌、异养菌、TMX降解菌的最大比生长速率,取值分别为0.8、6、6/d；SNH、SNO、SO分别为溶解性氨氮、溶解性硝酸盐氮及溶解氧的质量浓度。

1.5抑制常数测定及模型验证

1.5.1抑制常数测定

抑制常数的测定采用以呼吸速率为基础活性污泥抑制动力学常数的测定方法[19]。

非竞争性抑制是一些不参与反应过程的物质引起的。为确定非竞争性抑制的抑制常数,通过不投加和投加抑制物2个序批式反应过程来求解,2个序批式反应的起始质量浓度相同。在不投加和投加抑制物2种情况下的最大耗氧速率比的计算公式如下:

(13)

其中,KS为饱和常数;S0为起始质量浓度;I为抑制剂质量浓度;KI为抑制常数。

当出现最大耗氧速率时,KS一般远小于S0,因此有:

(14)

非竞争性抑制可以通过耗氧速率计算等速点底物质量浓度,再利用等速点底物质量浓度与抑制常数的关系求解抑制常数。

1.5.2模型验证

AGS试验在SBR中进行,装置高60 cm,内径10 cm,其有效体积为5 L,试验装置主要由反应器、进水与供气系统、控制系统、水箱和支架等部件组成。该实验设计2组反应器R1和R2，R1中添加TMX,R2中不添加TMX,分别运行。

本实验所用的原水为人工配水,C、N、P按质量比为100∶5∶1投加。保持2个反应器进水的化学需氧量(chemical oxygen demand,COD)均为1 kg/m3。培养200 d,颗粒成熟粒径达1.2 mm左右。通过实验验证模型的准确性与实用性。

1.6模型的结构

本文用AQUASIM[13]应用软件建立以生物膜数学模型为基础的一维颗粒污泥数学模型[20-21],模拟SBR中颗粒污泥的生长和代谢等活动,在AQUASIM程序中定义4个反应器来模拟AGS的SBR[22],其连接如图1所示。生物膜反应器的体积包含了SBR中总的颗粒污泥体积和部分液相体积,而完全混合式反应器中则包含了剩余的液相体积。在生物膜反应器和完全混合式反应器之间设置回流,回流比设置足够高,从而保证生物膜反应器中的液相底物质量浓度与完全混合式反应器中的底物质量浓度一致[17]。

图1　AQUASIM软件模拟AGS的SBR示意图

本研究模拟了SBR内AGS的生长,模拟操作周期为6 h,其中进水15 min,曝气300 min,静止30 min,出水15 min。模拟操作天数为200 d。

2结果与讨论

2.1抑制常数测定及模型验证

2.1.1抑制常数测定

本文测定不添加TMX和添加TMX 2组实验条件下的耗氧速率(oxygen uptake rate,OUR),结果如图2所示。

图2表明,TMX对SBR中微生物的耗氧速率有明显的抑制作用。不加TMX时反应器中微生物的最大耗氧速率为72.69 g/(m3·h),加入TMX时反应器中微生物的最大耗氧速率为36.5 g/(m3·h)。此时，由(14)式可计算出KI为19.8 g/m3。

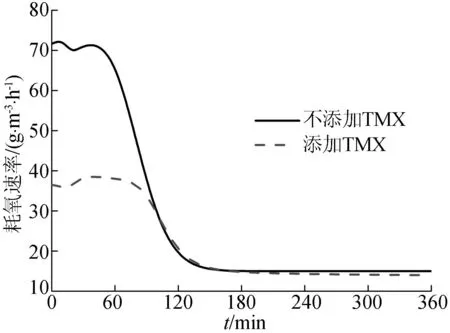
图2　非竞争抑制下的耗氧速率实测结果

2.1.2模型验证

在相同条件下,反应器中COD降解变化情况如图3所示。

图3　实验测定与模拟的COD降解曲线

由图3可知,R1中加入TMX后微生物的生长反应过程明显变慢,从而导致COD消耗速率变慢。模拟和实验数据均反映了抑制作用的存在，且数据基本趋势吻合较好，这说明基于ASM1模型建立的抑制模型能很好地模拟SBR中的运行情况。

2.2颗粒生长及其内部生物量分布

本研究模拟了2组实验室规模的SBR运行情况,R1添加TMX,R2不添加TMX,2组反应器分别模拟200 d。由于TMX具有一定毒性,故会对R1中微生物的生长产生一定抑制作用。2组反应器中颗粒的生长及内部微生物总量的变化情况如图4所示,图4验证了TMX在反应器运行过程中对其颗粒内微生物生长过程的抑制作用。

由图4a可看出,R1反应器内的颗粒在70 d左右达到最大值为1.1 mm,而R2反应器中的颗粒则在50 d左右就达到最大值为1.2 mm。R1反应器中颗粒增长速率以及颗粒成熟后的粒径均比R2反应器的小。这说明TMX对反应器中微生物的生长产生了抑制作用,使颗粒的增长速率变慢。

由图4b和图4c可看出,各微生物总量均为增长趋势,且增长趋势和颗粒的生长趋势相符合。R1中的自养菌、异养菌的生长速率及颗粒成熟后生物量总量均小于R2,这也反映了TMX对R1中自养菌和异养菌生长有着非竞争性抑制作用,降低了其生长速率,同时也降低了其生物总量。

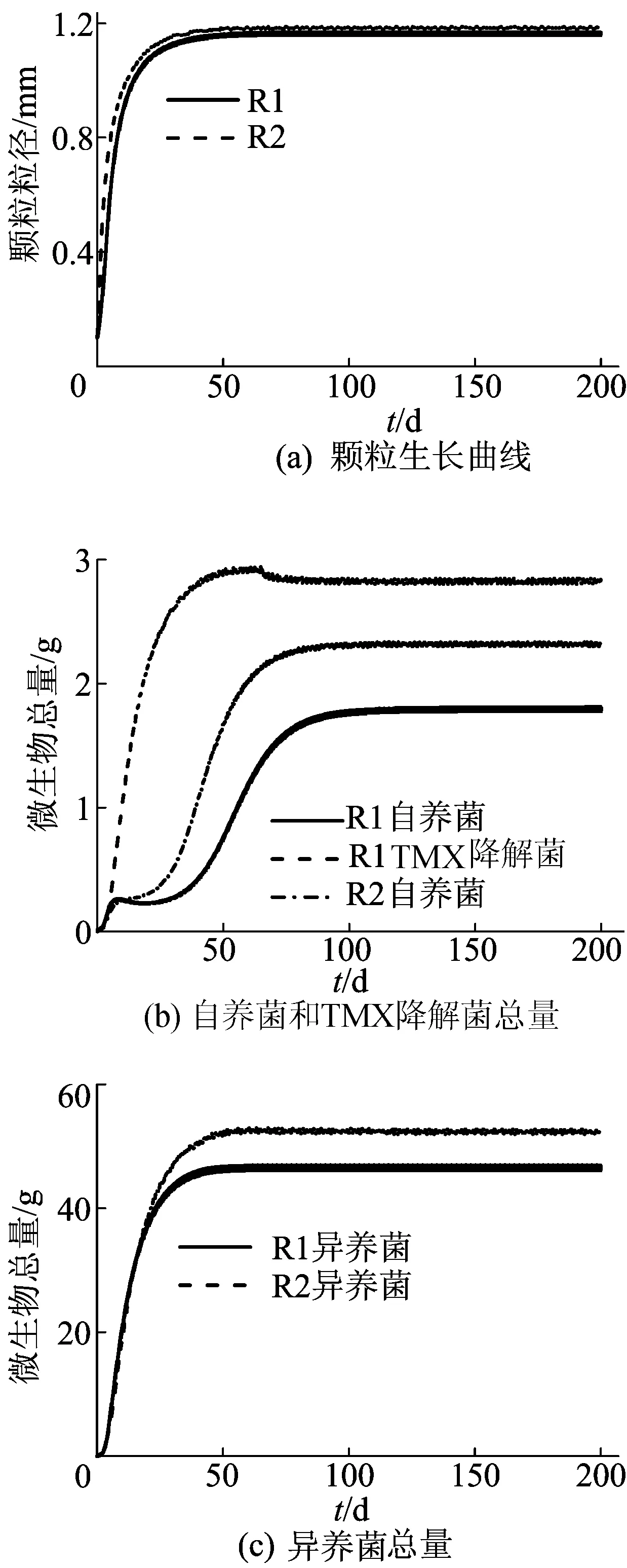
图4　AGS粒径及微生物总量变化

2.3反应器中周期内有机底物的去除

一个周期内反应器中COD、TMX的去除情况如图5所示。

由图5可看出，R1中COD降解的速率明显小于R2。取生长状态的25 ～25.25 d这个周期来进行比较,R1中COD在225 min左右消耗完成,而R2中的COD则在125 min左右就已经消耗完成,R1中COD的降解速率远远低于R2。这说明TMX抑制了R1中可降解有机底物的消耗速率。取颗粒成熟后70.0～70.25 d这一周期来进行比较,由图5可以看出,2个反应器中COD的降解速率相差不大,TMX的抑制作用已不明显。这是因为在颗粒成熟后R1中的TMX降解速率较快,反应器中存留的TMX较少,对微生物的生长抑制作用减弱,故在颗粒成熟后2个反应器中COD的降解速率相差不大。

图5　一个周期内反应器中COD和TMX的去除情况

2.4颗粒内部各物质的分布

DO、TMX从液相进入颗粒内部时存在传质阻力,会产生质量浓度梯度,如图6所示。

由于传质阻力的存在,DO在颗粒外层质量浓度高,内层质量浓度低。在一个周期内,液相中的营养物不断被颗粒内部的微生物消耗,颗粒内部微生物活性也随着营养物的减少而不断降低,氧气在颗粒内部的代谢速率也随之减少,颗粒内部DO质量浓度会相应增加[23-24]。模拟结果表明,在一个周期的前170 min颗粒内部的DO质量浓度很低,传质深度为200 μm,在170 min后颗粒内部的DO质量浓度明显增大,传质深度为600 μm。

AGS在SBR中由于瞬时质量浓度较高,溶解性物质可能完全渗透进入颗粒内部[3],故TMX在颗粒内外层有一定的质量浓度差,但其相差不大。

DO在颗粒内部的渗透深度是决定颗粒内部不同组分转化和营养物质去除效率和微生物种群空间分布的关键[25]。当颗粒内DO不足时,自养菌和异养菌会在颗粒内部竞争DO和空间位置。DO的扩散限制会降低硝化速率，不利于自养菌的生长[26],同时由于其本身较慢的生长速率,自养菌只有在高质量浓度DO和氨氮的外层才能同异养菌竞争DO和空间位置。在AGS系统中,营养物质一般分布在整个颗粒内,其并不是限制因素[27],因此异养菌在整个颗粒各个层面都能得到充分的营养物质，且分布在整个颗粒污泥内。

图6　TMX和DO在AGS内的分布情况

微生物在AGS内分布情况如图7所示,由图7可看出,自养菌主要是依赖DO进行好氧生长,故受DO传质限制,颗粒内部自养菌没有竞争优势,质量浓度较小,外部质量浓度较大。同时受TMX非竞争性抑制,R1颗粒内自养菌质量浓度低于R2颗粒内自养菌质量浓度。异养菌的生长分为好氧生长和缺氧生长。在未加入TMX的R2中,异养菌的生长未受到毒性物质的非竞争性抑制,在颗粒内部营养物质充足可以硝态氮为电子受体进行缺氧生长,也可以在DO充足的颗粒外层进行以氧气为电子受体的好氧生长，所以异养菌在颗粒内部分布较均匀。在加入TMX的R1中,TMX对异养菌产生一定的非竞争性抑制作用,导致异养菌在颗粒内部的分布为内部高外部低。TMX降解菌主要是依靠DO和TMX进行好氧生长,故在DO和TMX含量丰富的颗粒外层,TMX降解菌的质量浓度较高,颗粒内部质量浓度较低。

图7　微生物在AGS内的分布情况

3结论

本研究在ASM1的基础上运用AQUASIM软件建立AGS数学模型及抑制模型,通过实验不仅验证了该模型的准确性与实用性,同时也测得了抑制动力学中TMX的抑制常数为19.8 g/m3。

TMX对颗粒及微生物的生长和反应器中有机底物的去除均有明显的抑制作用。抑制条件下颗粒的最大粒径为1.1 mm,有机底物在225 min左右去除完成;非抑制条件下颗粒的最大粒径为1.2 mm,有机底物在125 min左右去除完成。抑制条件下自养菌和异养菌的总量明显小于非抑制条件下相应微生物的总量。

DO、TMX在颗粒内部分布趋势为颗粒外部质量浓度高,内部低。DO的传质深度为200 ～600 μm。在每个周期的初始阶段由于微生物生长活跃，颗粒内部的DO质量浓度较低,在中后期,颗粒内部DO的质量浓度较高。

自养菌、TMX降解菌主要分布在颗粒的外部。异养菌在不添加TMX时均匀分布在颗粒内部,而在添加TMX时由于受其非竞争性抑制作用，异养菌在颗粒内部质量浓度高,外部质量浓度低。

[参考文献]

[1]Shi X Y,Yu H Q,Sun Y J,et al.Characteristices of aerobic granules rich in autotrophic ammonium-oxidizing bacteria in a sequencing batch reactor[J].Chemical Engineering Journal,2009,147(2/3):102-109.

[2]周曼,杨昌柱,濮文虹,等.不同颗粒龄的好氧颗粒污泥性能的研究[J].环境科学,2012,33(3):896-902.

[3]倪丙杰.好氧颗粒污泥的培养过程、作用机制及数学模拟[D].合肥:中国科学技术大学,2009.

[4]Su K Z,Yu H Q.Formation and characterization of aerobic granules in a sequencing batch reactor treating soybean-processing wastewater[J].Environmental Science &Technology,2005,39(8):2818-2827.

[5]Su K Z,Yu H Q.A generalized model for aerobic granule-based sequencing batch reactor：1.model development[J].Environmental Science &Technology,2006,40(15):4703-4708.

[6]Lim J J,Kim M H,Kim M J,et al.A systematic model calibration methodology based on multiple errors minimization method for the optimal parameter estimation of ASM1[J].Korean Journal of Chemical Engineering,2012,29(3):291-303.

[7]王畅,苏馈足,邓绣坤,等.活性污泥颗粒化过程中絮体与颗粒污泥竞争作用研究[J].合肥工业大学学报:自然科学版,2011,34(10):1536-1539.

[8]Moy B Y,Tay J H,Toh S K,et al.High organic loading influences the physical characteristics of aerobic sludge granules[J].Letters in Applied Microbiology,2002,34(6):407-412.

[9]Sun X F,Liu C Y,Ma Y,et al.Enhanced Cu(Ⅱ)and Cr(Ⅵ)biosorption capacity on poly(ethylenimine)grafted aerobic granular sludge[J].Colloids and Surface B:Biointerfaces,2011,82(2):456-462.

[10]de Urzedo A P,Diniz M E,Nascentes C C,et al.Photolytic degradation of the insecticides thiamethoxam in aqueous medium monitored by directinfusion electrospray ionization mass spectrometry[J].Journal of Mass Spectrometry,2007,42(10):1319-1325.

[11]徐向阳,谢雨生,叶敏,等.硝基氯苯生产废水中典型有机污染物及其生物可处理性的初步研究[J].浙江大学学报:农业与生命科学版,2000,126(4):404-408.

[12]巫建光,孙亚敏,张之源.宣纸废水处理工艺运行控制条件的研究[J].合肥工业大学学报:自然科学版,2013,36(2):208-211.

[13]Reichert P.AQUASIM2.0-user manual：computer program for the identification and simulation of aquatic systems[Z].Swiss Federal Institute for Environmental Science &Technology(EAWAG),1998.

[14]国际水协废水生物处理设计与运行数学模型课题组.活性污泥数学模型[M].张亚雷,李咏梅,译.上海:同济大学出版社,2003:9-11.

[15]董峰,张捍民,杨凤林.数学模拟好氧颗粒污泥的形成及水力剪切强度对颗粒粒径的影响[J].环境科学,2012,33(1):181-190.

[16]Nicolella C,van Loosdrecht M C M,Heijnen J J.Mass transfer and reaction in a biofilm airlift suspension reactor[J].Chemical Engineering Science,1998,53(15):2743-2753.

[17]Henze M,van Loosdrecht M C M,Ekama G A,et al.污水生物处理:原理、设计与模拟[M].施汉昌,胡志荣,周军,等，译.北京:中国建筑工业出版社,2011:271-273.

[18]IAWPRC task group on mathematical modelling for design and operation of biological wastewater treatment.Activated sludge model No.1:scientific and technical reports[R].IAWPRC,1987.

[19]宋英豪,王凯军,倪文,等.以呼吸速率为基础活性污泥抑制动力学常数的测定研究[J].环境工程学报,2008,2(4):493-497.

[20]Wanner O,Reichert P.Mathematical modelling of mixed-culture biofilms[J].Biotechnology and Bioengineering,1996,49(2):172-184.

[21]Vázquez-Padin J R,Mosquera-Corral A,Campos J L,et al.Modelling aerobic granular SBR at variable COD/N ratios including accurate description of total solids concentration[J].Biochemical Engineering Journal,2010,49(2):173-184.

[22]Beun J J,Heijnen J J,van Loosdrecht M C M.N-removal in a granular sludge sequencing batch airlift reactor[J].Biotechnology and Bioengineering，2001,75(1)：82-92.

[23]Zhou X H,Qiu Y Q,Shi H C,et al.A new approach to quantify spatial distribution of biofilm kinetic parameters by in situ determination of oxygen uptake rate(OUR)[J].Environmental Science &Technology,2008,43(3):757-763.

[24]Li Y,Liu Y,Shen L,et al.DO diffusion profile in aerobic granule and its microbiological implications[J].Enzyme and Microbial Technology,2008,43(4/5):349-354.

[25]de Kreuk M K,Picioreanu C,Hosseini M,et al.Kinetic model of a granular sludge SBR:influences on nutrient removal[J].Biotechnology and Bioengineering,2007,97(4):801-815.

[26]van Benthum W A J,van Loosdrecht M D M,Heijnen J J.Control of heterotrophic layer formation on nitrifying biofilms in a biofilm airlift suspension reactor[J].Biotechnology and Bioengineering,1997,53(4):397-405.

[27]Li Y,Liu Y.Diffusion of substrate and oxygen in aerobic granule[J].Biochemical Engineering Journal,2005,27(1):45-52.

(责任编辑闫杏丽)

Study of the effect of thiamethoxam on activated sludge granulation by mathematical model

ZHANG Ming,SU Kui-zu,BAO Bai-ling

(School of Civil and Hydraulic Engineering,Hefei University of Technology,Hefei 230009,China)

Abstract:Based on the activated sludge model 1(ASM1),the mathematical model of aerobic granule was established with inhibition kinetics with AquaSim software.The model was used to simulate the sequencing batch reactor(SBR)operation with and without inhibition of thiamethoxam(TMX)respectively.The aerobic granule process such as the growth of the particles,the nutrients removal,the growth of microorganism,the distribution profiles of TMX and dissolved oxygen(DO)as well as the spatial distribution of autotrophic bacteria,heterotrophic bacteria and TMX degrading bacteria in aerobic granular sludge(AGS)were simulated well by this model.The results showed that TMX had noncompetitive inhibitory effect on the autotrophic bacteria and heterotrophic bacteria,and had substrate inhibitory effect on TMX degrading bacteria.And DO had important influence on the spatial distribution of aerobic microbial population.The depth of the mass transfer of DO was 200-600 μm in aerobic granular sludge.Hence,autotrophic bacteria and TMX degrading bacteria based on oxygen located primarily in the outer space of particles.Heterotrophic bacteria distributed uniformly in the whole particles without TMX.When TMX was added to the SBR,the heterotrophic bacteria spatial distribution shows more in the inside of the particles but less in the outer space owing to TMX noncompetitive inhibition of heterotrophic bacteria.

Key words:aerobic granular sludge(AGS);mathematical model;inhibition;thiamethoxam(TMX)

收稿日期：2015-01-29；修回日期：2015-03-05

基金项目：国家自然科学基金资助项目(51378165)

作者简介：张明(1989-),男,安徽当涂人,合肥工业大学硕士生;苏馈足(1977-),女,河北衡水人,博士,合肥工业大学教授,硕士生导师.

doi:10.3969/j.issn.1003-5060.2016.04.020

中图分类号:X703.1

文献标识码：A

文章编号：1003-5060(2016)04-0529-07