复材非线性及渐进损伤的态型近场动力学模拟

刘肃肃,余　音

(上海交通大学 航空航天学院,上海 200240)



复材非线性及渐进损伤的态型近场动力学模拟

刘肃肃,余音

(上海交通大学 航空航天学院,上海 200240)

摘要:为了实现复合材料材料非线性行为在态型近场动力学的模拟,引入单参量非线性本构模型来确定态型近场动力学中力状态与变形状态之间的非线性关系.为了实现复合材料渐进损伤行为的态型近场动力学模拟,在力状态表达式中引入一个标量函数,以实现利用强度准则判断物质点之间作用力是否失效.采用动力松弛法作为数值求解方法.结果显示,模型计算得到的单向复合材料板(AS4/PEEK)的非线性应力-应变曲线与试验数据吻合良好；对中心含孔复合材料板的渐进损伤模拟则表明,该模型模拟的破坏形式与已有研究的模拟结果及实验观察结果一致.探索和实现了复合材料非线性本构在态型近场动力学中的引入以及复合材料渐进损伤在态型近场动力学中的模拟.

关键词：近场动力学；复合材料；非线性；渐进损伤；动力松弛法

近场动力学(peridynamic theory, PD)[1-2]是一种新兴的基于非局部作用思想的理论.不同于传统理论的是,该理论采用积分形式构建运动方程,在解决诸多不连续问题方面具有独特的优势.近年来,PD理论受到了广泛的关注并得到了迅速的发展.黄丹等[3]对PD的基本方法及其相关应用进行了介绍,并将PD应用于模拟混凝土的冲击破坏过程[4]；胡祎乐等[5]则将PD应用于分析复合材料层压板的渐进损伤；孙璐妍[6]在研究中建立了金属平板和曲板稳定性分析的PD模型.

最初的键型近场动力学理论(bond-based peridynamics)[1]在采用对点力函数(pairwise force function)来描述物质点之间的相互作用力时,存在一定的不足[3,7].这种对点力函数假设认为两物质点之间的相互作用力是等大反向的,并且未考虑邻域内其他因素(如其他物质点及物质点间作用力)对该作用力的影响,在描述各向同性、线弹性材料时,其泊松比只能局限于0.25.此外,在应用该理论描述金属材料的塑性时,也会出现与实验现象相矛盾的结果[3,7].为了解决上述问题,Silling等[7-8]提出态型近场动力学理论(state-based peridynamics),该理论不仅可以应用于不同泊松比的材料,同时也可以在PD理论框架下实现一些经典力学模型的应用：Foster等[9]在态型PD理论中利用金属塑性理论分析了6061-T6铝合金的粘塑性响应；Tupek等[10]则在态型PD理论中整合了经典力学破坏模型,模拟了6061-T6铝合金在冲击载荷下的破坏过程及单轴拉伸载荷下的力学响应.

已有的复合材料PD模型多采用键型PD理论进行建模：Askari等[11]在用键型PD理论对复合材料进行建模时,分别采用纤维键和基体键来考虑纤维和基体的不同性能；Killic等[12]将单向复合材料离散成纤维域和基体域,两者之间的比例可以反映纤维体积含量；Hu等[13]则采用宏观偏轴模量来等效确定复合材料层内键的大小.这些模型给出了与实验现象相符的破坏模式,对宏观等效性能的精确定量分析还比较缺乏,相关的定量分析也多在线弹性范围内,既能准确预测复材材料非线性行为、又能描述其损伤行为的PD模型有待进一步研究.

本文采用态型PD理论对复合材料进行建模,采用经典单参量非线性本构模型确定力状态与变形状态之间的关系,并在损伤描述中引入传统的强度准则.为验证模型的有效性,编写了数值计算程序,并对AS4/PEEK复合材料在单轴拉伸载荷作用下的材料非线性行为及渐进损伤过程进行模拟,与文献中的实验结果及有限元的计算结果进行对比.

1态型近场动力学理论简介

近场动力学将物体离散成一系列物质点,在物体参考构型R内,物质点x存在半径为δ的邻域(Horizon)H,在该邻域内物质点x与其他物质点x′存在相互作用.记物质点x与物质点x′的初始坐标分别为x和x′,位移分别为u和u′,则两物质点的相对位置和相对位移可分别表示为ξ=x′-x,η=u′-u,如图1所示.

图1　参考构型与邻域Fig.1　Reference configuration and horizon

在近场动力学中,物质点x上建立运动方程为

(1)

(2)

(3)

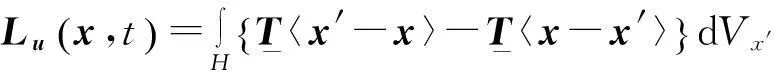
(4)

Silling等[7]通过与经典理论中应变能密度等效的方式得到了变形梯度的表达式：

(5)

(6)

2单参量模型

2.1单参量非线性本构

在表征复合材料物理非线性的宏观力学理论模型中,由Sun等[14]提出的单参量模型能够较为准确地描述单向复合材料在偏轴载荷作用下的非线性响应.在平面应力状态下,该模型在假设纤维方向为线弹性的基础上,获得了仅含单参量的塑性势能函数表达式：

(7)

(8)

式中:A和n为拟合参数.将总的应变增量分为弹性部分增量dεe和塑性部分增量dεp,dε=dεe+dεp.结合流动法则,塑性应变增量为

(9)

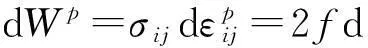
(10)

该塑性功增量又可表示为等效应力与等效塑性应变增量的乘积形式：

(11)

(12)

塑性应变增量的表达式可联立式(7)、(8)、(9)和(12)得到

(13)

dε=Sdσ,

式中:S为柔度阵.根据式(13)结合复合材料弹性理论可得到柔度阵为

(14)

式中:E1、E2、E12为弹性模量,ν12为泊松比.

定义塑性泊松比为

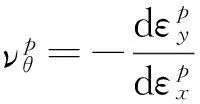
(15)

(16)

2.2强度准则

Sun等[15]在对AS4/PEEK单向复合材料在各偏轴拉伸载荷作用下的强度进行测试后,认为其强度准则为

(17)

(18)

式中:Y和S分别为横向拉伸强度及剪切强度.

3含非线性本构及损伤描述的态型PD模型

3.1本构方程

在态型近场动力学理论中,力状态与应力张量σ之间存在以下关系[7]：

(19)

将式(19)表示为增量形式,应力增量可用应变增量表示,相应的力状态增量为

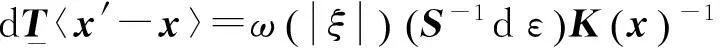
(20)

位移梯度可以用变形梯度式(5)表示

▽u=F-I.

(21)

式中:I为单位阵.则应变张量为

(22)

将式(5)代入式(22),再代入式(20),得到

(23)

3.2损伤描述

一些复合材料PD模型[11-13]在采用键理论分析损伤问题时,一般采用键的临界伸长率作为键是否失效的判断依据.然而材料的损伤特性也有可能取决于其他状态参量[10,15],如应力状态等.本文尝试了一种利用强度准则判断损伤是否发生的方法,为损伤在态型PD理论中的描述提供参考.

(24)

式中:D和D′分别为键ξ两端物质点x与物质点x′的损伤参量.首先判断键ξ是纤维键还是基体键(本文中键的方向与纤维铺层方向一致则为纤维键,否则为基体键)：若为纤维键,则采用式(17)中的“纤维断裂”判据判断键两端物质点处的应力状态,达到判据的物质点对应的D(或D′)值取为1,否则取值为0；若为基体键,则采用式(17)中的“基体破坏”判据对键两端物质点的D(D′)值进行判断.

将式(24)引入式(20)得到

(25)

如此,即可根据式(24)、 (25),依据式(17)的强度准则对两物质点之间作用力是否失效作出判断.式(25)的力状态表达式中包含了损伤和断裂的描述,可用于描述裂纹萌生和扩展过程.

进一步,物质点x处损伤程度可用损伤指数φ进行表征：

(26)

4数值方法

4.1离散化方法

对模型进行均匀离散化,并采用黎曼和对积分项进行求解.根据式(5)和 (6),得到物质点xj处的变形梯度和形状张量分别为

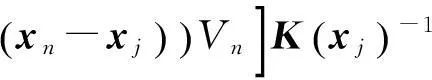
(27)

(28)

式中:xn和xj分别为物质点n和物质点j的位置矢量,m为物质点j邻域H范围内的物质点总数,Vn为物质点n的体积.将式(3)代入式(27)、再代入式(22)得到物质点xj处的非局部应变张量为

(29)

式中:un和uj分别为物质点n和物质点j的位移矢量.式(29)即为物质点j处的非局部应变,由该物质点邻域H范围内的位移场计算得到.

4.2数值求解

动力松弛法是一种应用广泛的数值求解方法.在应用于静力问题时,动力松弛法可采用虚拟质量和虚拟阻尼,进而将静力问题转化成动力问题来进行求解.在施加初始增量步之后,系统首先在不平衡力的作用下发生运动,而后在迭代过程中不平衡力逐渐减小,系统动能也在阻尼作用下渐趋于零,最后达到静力平衡状态.依据达朗贝尔原理,第n次迭代时物质点的运动方程为

(30)

(31)

整理得

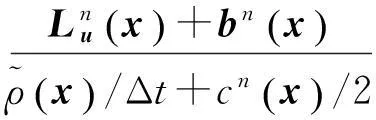
(32)

(33)

在求解静力问题时,虚拟密度、虚拟阻尼与计算结果无关,但会影响计算稳定性和收敛速度[16].一般取Δt=1,将虚拟密度阵设为如下对角形式：

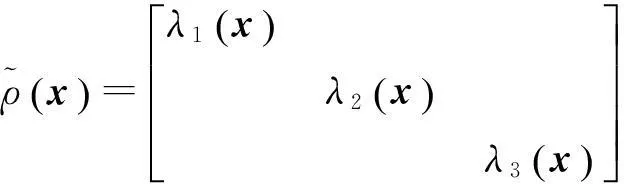
(34)

则对角元素与Δt需满足以下关系式[17]：

(35)

式中:Q为平衡方程中的刚度阵.第n次迭代的虚拟阻尼可按以下表达式确定[17]：

(36)

i=1,2,3.

(37)

4.3收敛准则

采用相对位移收敛准则判断物质点是否达到平衡状态：

(38)

5算例与结果

在第3、4章基础上编写了复合材料近场动力学模型的数值计算程序.在对模型进行均匀离散化之后,先给定离散点的位移边界条件及载荷条件,而后按照动力松弛法进行迭代求解.

为验证模型及程序的有效性,分别对AS4/PEEK复合材料中心无孔层压板和中心含孔层压板受单轴拉伸载荷作用的情况进行建模计算,并与试验及有限元结果进行对比.试验数据及材料参数来自文献[15,18],材料参数如表1所示.其中参数A1和A2分别为式(8)中算例5.1和算例5.2所取的A值.

表1　室温下AS4/PEEK复合材料的材料参数

5.1中心无孔层压板受偏轴拉伸

图2　中心无孔层压板受偏轴拉伸载荷示意图Fig.2　Laminate without a hole under off-axis tension load

中心无孔层压板受偏轴拉伸载荷作用的示意图如图2所示,单向复合材料板的纤维方向与载荷作用方向的夹角为θ,取层压板有效尺寸为190.5 mm×19.0 mm.在离散化建模时,取物质点间距Δx=0.5 mm,邻域半径按照文献[19]的建议取δ=3Δx,模型最终包含物质点总数为14 478个.边界条件为一边固支,另一边施加纵向固定位移,边界条件施加在两端的物质点上.

该模型的离散物质点数虽然不多,但是考虑到非线性迭代计算需要保证一定的增量步数,故而通过将各物质点的计算映射到计算机的单个线程的方式来实施并行运算,提高计算效率.

最终得到的偏轴拉伸应力-应变曲线与试验数据的对比结果如图3所示.图中εL为根据式(29)计算得到的层压板中心处物质点在拉伸方向的非局部应变,σL为相应物质点在拉伸方向上的应力.由图3可见,本模型的计算结果与试验数据吻合良好,误差小于9.2%.

图3　不同偏轴拉伸角度下应力-应变对比结果Fig.3　Stress-strain comparison under different off-axis tension angles

如图4所示给出了不同偏轴角度下层压板中心处物质点的塑性泊松比的对比结果.可见,各偏轴角度下由本模型计算所得的塑性泊松比相对式(16)的理论值更接近于试验值.

图4　不同偏轴角度下塑性泊松比的对比结果Fig.4　Plastic Poisson’s ratios comparison under different off-axis tension angles

5.2中心含孔层压板受轴向拉伸

中心含孔层压板受轴向拉伸载荷作用的示意图如图5所示,复合材料层压板的纤维方向与载荷作用方向一致,取层压板有效尺寸177.5 mm×45.5 mm.在离散化建模时,本算例仍然取物质点间距Δx=0.5 mm,邻域半径δ=3Δx,最终模型包含物质点总数为30 853个.中心圆孔半径为20.5 mm,圆孔周边p1处沿环向贴有应变片,p1与圆孔中心的位置关系见图6.按模型离散点位置,本模型实际所取角φ=32.27°.根据本模型得到的远端应力σR-孔边应变εH曲线与试验数据的对比结果如图6所示,两者在应变较小处吻合良好,但在应变较大处出现了差异.这种差异可能是由于单参量塑性模型的参数是在比例加载情况下得到的,只能近似适用于孔边的受力状态[18].

图5　中心含孔层压板受轴向拉伸载荷示意图Fig.5　Laminate with a centre-hole under axis tension load

图6　中心含孔层压板远端应力—孔边应变曲线对比Fig.6　Remote stress-hoop strain curve comparison for laminate with a centre-hole

如图7和8所示分别给出了端部产生总长度1%的位移时,纵向(载荷作用方向)与横向的位移场分布云图.损伤指数φ采用式(26)进行表征.(a)和(b)分别为有限元(FEM)的计算结果和本模型的计算结果.由图7、8可见两者的纵向位移场分布几乎没有差别.在横向的位移场分布上,由有限元计算所得的正向与反向的最大位移分别为0.320和-0.324 mm,PD计算得到的则对应为0.387和-0.391 mm,但在[-0.324,0.320]范围外的位移仅分布在靠近圆孔周边的少量物质点上.总体而言, PD计算所得的位移场分布与有限元的计算结果相一致.

图7　纵向位移场分布云图Fig.7　Displacement filed distribution in longitudinal direction

图8　横向位移场分布云图Fig.8 Displacement filed distribution in transverse direction

5.3中心含孔层压板的渐进损伤模拟

由于近场动力学的优势主要体现在分析不连续问题,本文采用第3节所述的损伤描述方法对中心含孔层压板受拉伸载荷作用下的渐进损伤进行了模拟.损伤程度采用式(26)进行表征,没有损伤时损伤指数为0,完全损伤后为1.选用5.2节所述的层压板尺寸及离散化参数,纤维方向与拉伸载荷作用方向分别取0°、45°、90°.如图9所示给出了本模型各角度铺层层压板的渐进损伤模拟结果,可见在单轴拉伸载荷作用下各角度铺层层压板的损伤均起始于圆孔周围,而后损伤沿纤维方向发生扩展.对比已有研究[20]中对纤维增强树脂基复合材料的模拟结果以及实验观察结果(见图10的(a)、(b)),本模型模拟的各铺层角度下的破坏形式与文献[20]基本相符合.

图9　各角度下的渐进损伤模拟结果Fig.9　Progress damage results under different angles

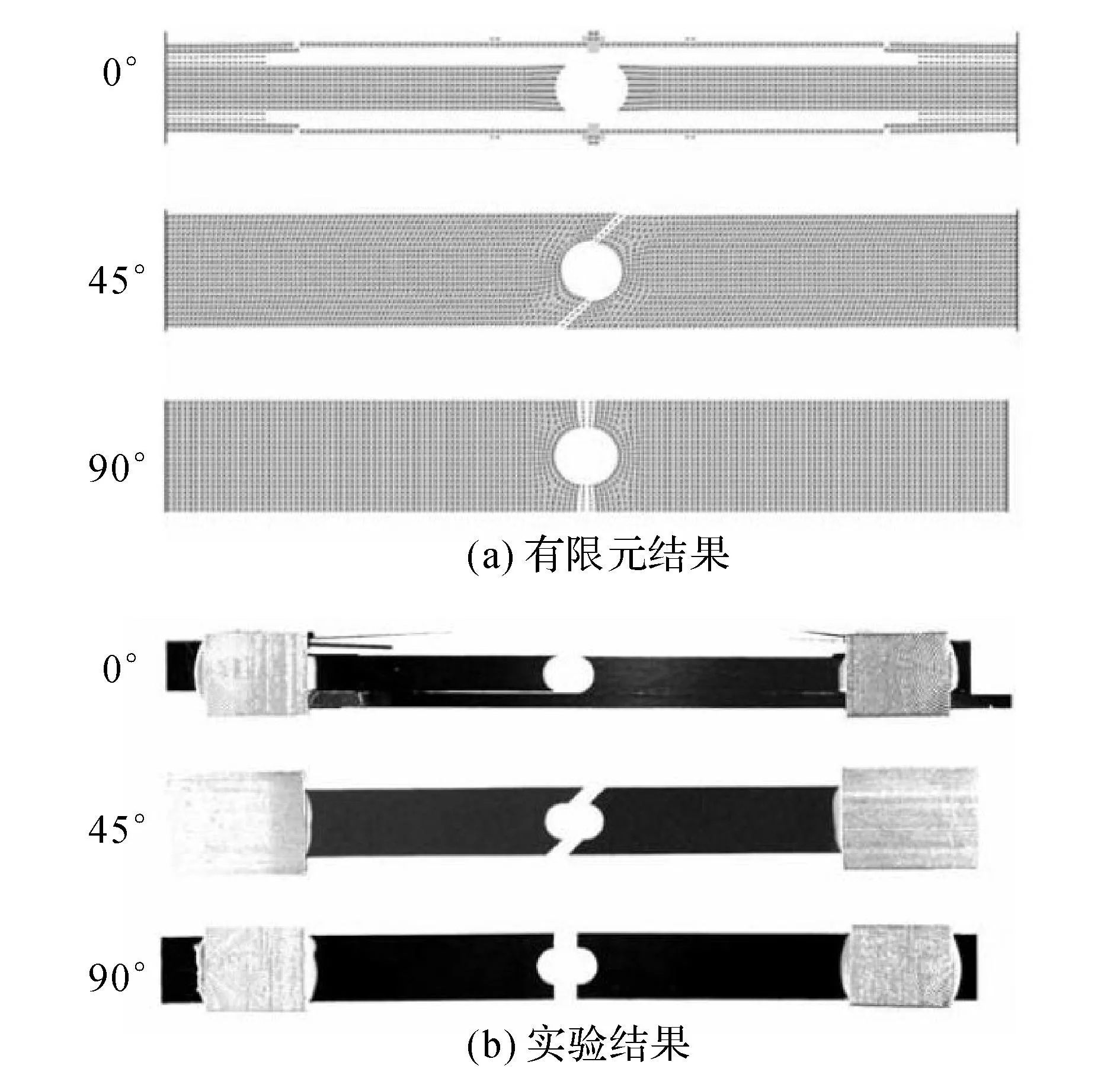
图10　已有研究中的有限元模拟及实验结果[20]Fig.10　FEM and experimental results of a relevant research[20]

6结论

(1)本研究采用了态型近场动力学对复合材料进行建模,通过引入单参量非线性本构来确定力状态与变形状态之间的关系.采用该模型计算了中心无孔AS4/PEEK单向复合材料板在偏轴拉伸载荷下的力学响应.结果显示,由本模型计算得到各偏轴角度下的应力-应变曲线与试验数据吻合良好.

(2)对中心含孔层压板受轴向拉伸情况的计算表明,本模型得到的远端应力-孔边应变曲线在应变较小处吻合良好.计算得到的位移场分布与有限元的计算结果相一致.

(3)在力状态表达式中引入一个标量函数,以实现利用强度准则判断物质点之间作用力是否失效,从而模拟复合材料的渐进损伤过程.对中心含孔层压板的渐进损伤模拟表明,损伤最初起始于孔边,而后沿纤维方向发生扩展.由本模型模拟的各角度下的破坏形式与有关研究中对纤维增强树脂基复合材料的模拟结果以及实验观察结果相一致.

(4)通过以上算例,模型的有效性得以验证,实现了复合材料非线性及渐进损伤在态型近场动力学中的模拟,为复合材料在态型近场动力学中的建模提供新的思路与方法.

参考文献(References)：[1] SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces [J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209．

[2] EMMRICH E, LEHOUCQ R B, PUHST D. Meshfree Methods for Partial Differential Equations VI[M]. Berlin Heidelberg:Springer, 2013: 45-65．

[3] 黄丹, 章青, 乔丕忠,等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40 (4):448-459.

HUANG Dan,ZHANG Qing,QIAO Pei-zhong,et al. A review on peridynamics(PD) method and its application [J].Advances in Mechanics, 2010, 40 (4):448-459．

[4] 沈峰, 章青, 黄丹,等. 冲击荷载作用下混凝土结构破坏过程的近场动力学模拟[J]. 工程力学, 2012, 29(A01):12-15．

SHEN Feng,ZHANG Qing,HUANG Dan,et al. Peridynamic Modeling of failure process of concrete structures subjected to impacting load [J].Engineering Mechanics, 2012, 29(A01):12-15．

[5] 胡祎乐, 余音, 汪海. 基于近场动力学理论的层压板损伤分析方法[J]. 力学学报, 2013, 45(4):624-628．

HU Yi-le,YU Yin,WANG Hai. Damage analysis method for laminates based on peridynamic theory [J].Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4):624-628．

[6] 孙璐妍. 基于近场动力学的金属板稳定性分析方法研究[D]. 上海: 上海交通大学, 2014．

SUN Lu-yan. Stability analysis method study of metallic plates based on peridynamics[D]. Shanghai: Shanghai Jiao Tong University, 2014．

[7] SILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling [J]. Journal of Elasticity, 2007, 88(2):151-184．

[8] SILLING S A. Linearized theory of peridynamic states[J]. Journal of Elasticity, 2010, 99(1):85-111．

[9] FOSTER J T, SILLING S A, CHEN W W. Viscoplasticity using peridynamics[J]. International Journal for Numerical Methods in Engineering, 2010, 81(10):1242-1258．

[10] TUPEKA M R, RIMOLIA J J ,RADOVITZKY R. An approach for incorporating classical continuum damage models in state-based peridynamics[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 263:20-26．

[11] ASKARI E, XU J F. Peridynamic analysis of damage and failure in composites [C]∥44th AIAA Aerospace Sciences Meeting and Exhibition. Reno, Nevada,Reston, VA:AIAA, 2006: 1-12．

[12] KILLIC B, AGWAI A, MADENCI E. Peridynamic theory for progressive damage prediction in center-cracked composite laminates [J]. Composite Structures, 2009, 90(2):141-151．

[13] HU Y L, YU Y, WANG H. Peridynamic analytical method for progressive damage in notched composite laminates [J]. Composite Structures, 2014, 108: 801-810.

[14] SUN C T, CHEN J L. A simple flow rule for characterizing nonlinear behavior of fiber composites[J]. Journal of Composite Materials, 1989, 23(10): 1009-1020．

[15] SUN C T, YOON K J. Characterization of elastic-plastic properties of AS4/APC-2 thermoplastic composite[R]. NASA-CR-183145, West Lafayette: School of Aeronautics and Astronautics, Purdue University, 1988．

[16] 单建, 蓝天. 动力松弛法在张拉结构静力分析中的应用[J]. 东南大学学报, 1994, 24(3):94-98．

SHAN Jian,LAN Tian. On dynamic relaxation and its application to static analysis of tension structures [J].Journal of Southeast University, 1994, 24(3):94-98．

[17] KILLIC B. Peridynamic theory for progressive failure prediction in homogeneous and heterogeneous materials[D]. Tucson: The University of Arizona, 2008.

[18] SUN C T, YOON K J. Elastic-plastic analysis of AS4/PEEK composite laminate using a one-parameter plasticity model [J]. Journal of Composite Materials, 1992, 26(2):293-308．

[19] SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics [J]. Computers and Structures, 2005, 83(17):1526-1535．

[20] LAS V, ZEMCIK R. Progressive damage of unidirectional composite panels [J]. Journal of Composite Materials, 2008, 42(1):25-44．

State-based peridynamic modeling of nonlinear behavior and progressive damage of composites

LIU Su-su, YU Yin

(SchoolofAeronauticsandAstronautics,ShanghaiJiaoTongUniversity,Shanghai200240,China)

Abstract:One-parameter nonlinear constitutive model was utilized to get the relationship between deformation vector state and force vector state for the sake of nonlinear behavior modeling of composites in state-based peridynamics. A scalar function was used so that strength criterion could be utilized for the validity judgment of the interaction between particles in order to model the progressive damage of composites in state-based peridynamics. Dynamic relaxation method was utilized as the solution method. The calculated nonlinear stress-strain relations of unidirectional composite panels (AS4/PEEK) accorded well with the test data. The progressive damage analysis results agreed with the experimental and simulating results of a relevant research. The method for nonlinear behavior and progressive damage modeling of composites in state-based peidynamics was explored and verified．

Key words:peridynamics; composite materials; nonlinear behavior; progressive damage; dynamic relaxation method

收稿日期：2015-10-26.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(11372192)；上海市自然科学基金资助项目(13ZR1422200)；上海市科委重大项目科技攻关资助项目(12DZ1100302).

作者简介：刘肃肃(1991-)，男，硕士生，从事复合材料结构强度等研究.ORCID: 0000-0002-2111-2074. E-mail: fowyaring@sjtu.edu.cn通信联系人：余音，女，副教授.ORCID: 0000-0003-3587-0260. E-mail: yuyin@sjtu.edu.cn

DOI:10.3785/j.issn.1008-973X.2016.05.025

中图分类号：TB 332

文献标志码：A

文章编号：1008-973X(2016)05-0993-08