基于实际换挡规律的卡车列队行驶起步控制

李明达,隗海林,门玉琢,包翠竹

(1.吉林大学 交通学院,吉林 长春 130022；2.长春工程学院 机电工程学院,吉林 长春 130012)



基于实际换挡规律的卡车列队行驶起步控制

李明达1,2,隗海林1,门玉琢2,包翠竹1

(1.吉林大学 交通学院,吉林 长春 130022；2.长春工程学院 机电工程学院,吉林 长春 130012)

摘要:为了解决卡车列队行驶起步过程中的控制问题,在车辆行驶3.5 万公里的实验数据中提取456 段起步过程的挡位数据,对该数据中各挡位的使用情况进行统计与分析.根据统计结果制定相应的换挡规则,利用自适应模糊控制算法设计车辆列队行驶的控制模型,在模型中通过跟随车辆的挡位信息对模糊控制器的输入量进行加权系数调整,提高控制算法的自适应性,通过TruckSim和Matlab的联合仿真,将实车实验数据作为头车模拟工况,模拟3辆卡车在车联网环境下的列队起步过程,仿真结果表明起步过程中的行驶间距误差可以控制在车辆单位时间内行驶距离的5%以内,具有一定的控制精度.

关键词：换挡规则；自适应模糊控制；列队行驶；TruckSim；Matlab；联合仿真

随着市场经济的快速发展,公路运输在我国国民经济中的地位越来越重要.据统计：2014年我国的货运总量为439.1亿吨,其中公路货运量为334.3亿吨,比上年末增长了8.7%[1]；拥有公路营运汽车1 537.93万辆,其中载货汽车1 453.36万辆,比上年末增长了2.4%[2].在这样的背景下,车辆列队行驶控制技术越来越受到人们关注和重视.有研究表明2辆重型卡车在时速80 km/h、间距10 m的工况下头车与跟随车辆分别节油6 %和20 %[3]；日本的研究表明如果40 %的重型卡车采用列队行驶的方式、以10 m间距行驶,那么CO2的排放将减少2.1 %[4].

国外对列队行驶控制技术的研究较早.20世纪90年代,Franke 等[5]建立了基于距离与加速度的2层控制器,实现了车辆的列队行驶；随后Gehrig等[6]通过弹性带算法探讨了列队行驶跟随系统的安全性问题；Gehring 等[7]采用滑模变结构的控制方法对2层控制器进行改进；Vinel等[8]对车辆时速在90 km/h、间距为12.5 m的工况进行分析；日本的Energy ITS项目采用5.8 GHz的无线通信模块搭建车联网进行车辆列队行驶实验[9].国内对列队行驶相关领域的研究起步较晚,但也有很多研究成果,例如：马育林等[10]在1∶10的模型道路中进行智能小车的列队行驶实验；高振海等[11]基于跟车行驶提出了一种基于粒子群算法的模糊自校正控制器参数优化方法；岳伟等[12]、任殿波等[13]也进行了相应的理论研究和系统仿真.

然而该研究内容还存在诸多问题.首先,大多数的车辆列队行驶研究都是基于复杂车辆数学模型,车辆模型的非线性和不确定性使得控制器的设计难度加大；其次,研究内容多为车辆稳定运行时的控制策略研究,对于起步过程中的列队行驶控制研究较少；再者,重型卡车挡位较多,驾驶员在实际驾驶过程中尤其对低速挡的操作上并非逐级换挡,而目前的换挡研究中,很少考虑驾驶员的实际换挡情况.

鉴此,针对以上问题对12挡商用车起步过程中的挡位变换规律进行分析,得到了实际的换挡规律,利用自适应模糊控制算法搭建了卡车列队行驶的控制模块,以实车的实验数据作为头车控制信息,采用TruckSim中的车辆模型与Matlab进行联合仿真,模拟车辆在间距和速度均可通过传感器进行精确测量并实时传输的工况下,按照实际的换挡规律对列队行驶车辆进行挡位、油门开度及制动过程的控制,以达到车辆间距和相对速度的稳定以及换挡过程的平稳.

1换挡规则及仿真基本参数

1.1换挡规则

为得到商用车的实际换挡规律,在6名驾驶员(驾龄均超过5 a、年行驶里程数超过1.0×105km、日均驾车时间超过8 h)驾驶12挡商用车在高速公路上行驶3.5万公里的实验数据中提取了456段起步过程的挡位数据并进行换挡情况的数据统计与分析.如图1所示为456段起步过程中挡位的使用情况,图中数值代表该挡位在起步过程中出现的概率.从图1中可以看出驾驶员对12挡商用车低速挡一般采用跳挡操作,即在驾驶员的起步换挡过程中是根据具体工况进行换挡的,并非逐级换挡,从图1中可以看出在低速挡换挡过程中3挡、4挡、5挡使用率接近于0,6挡使用概率相对较小,而高速挡一般采用逐级换挡,但11挡的使用率也相对较低.

图1　起步过程中挡位使用情况Fig.1　Usage of gears in start process

在实际驾驶过程中,驾驶员挡位的选择是基于本车速度与油门开度决定的,因此将实验数据中的挡位数据、车速v和油门开度αth绘制挡位分布情况如图2所示.

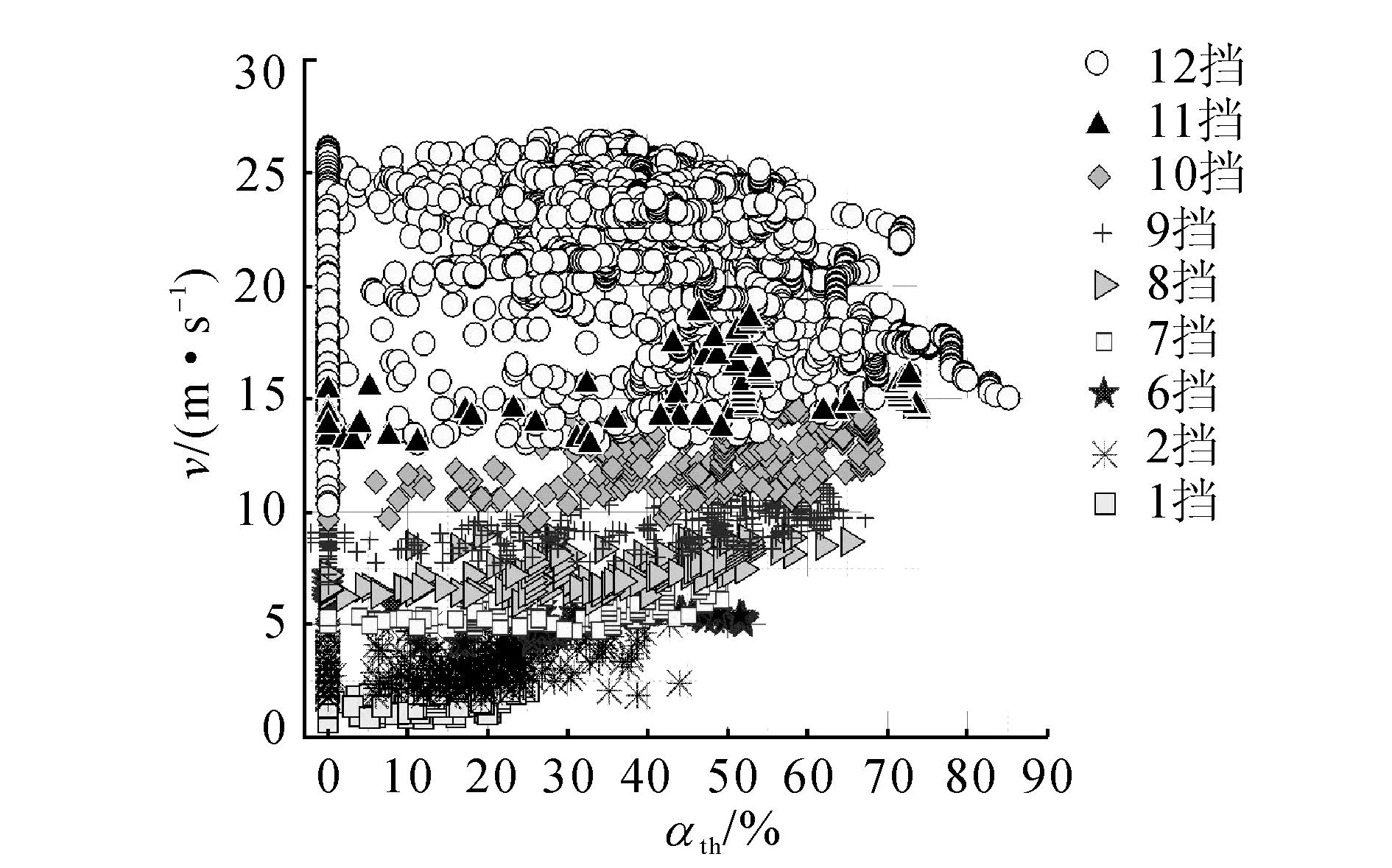
图2　起步过程中挡位分布图Fig.2　Distribution of gear status in start process

根据实际数据提取和分析挡位的使用与分布情况,制定相应的换挡规则.将图2中挡位数据进行区域划分和数据变换后如图3所示：图中no为变速箱输出转速.

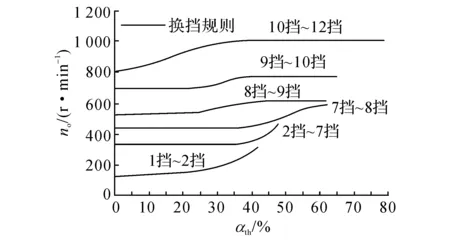
图3　起步过程换挡规则图Fig.3　Gearshift schedule map in start process

1.2仿真基本参数

由于采集的是12挡六轴半挂卡车的行驶数据,因此在TruckSim模拟仿真实验中头车与跟随车辆模型均设置为实车模型的基本参数,其车辆动力学参数如表1所示.表中,mv为整车质量,mc为货物质量,Tbr为车轮的制动力矩,rw为车轮半径,rv为有效车轮滚动半径,vabs为关闭ABS的车速范围,Pen为发动机功率,nr为发动机额定转速,So为ABS启动滑移率,Sc为ABS关闭滑移率,ηt为变速箱传动效率,i0为主减速比,i1至i12分别为1挡到12挡的减速比.

表1　卡车模型动力学参数

同时设置车辆换挡延时时间为0.5 s,该时间是指换挡指令发出到挡位更换完毕所使用的时间.车联网数据传输时间是指车辆间距、速度和加速度信息在无线网络传输过程中的延时,由于目前的无线通信设备传输周期约为20 ms,同时在车辆列队行驶过程中车辆间距不会很大,否则很难形成车队,影响整体的燃油经济性.因此在传输过程中即使有信号干扰,延时时间也不会很长.至于油门与制动踏板执行时间,由于油门与制动踏板位置由自适应模糊控制算法根据行驶间距与相对速度得出,且采用自动驾驶模式,这样保证控制精度的同时,也减少了人为产生的误操作,避免了反应时间过长,因此设置车联网传输延时与油门或制动执行时间之和为0.2 s.

设置车辆列队行驶的初始条件为跟随车辆与前车在未起动之前的间距为2 m.当头车按照实车速度起动时,跟随车辆根据与前车间距、相对速度以及车辆自身速度控制其油门开度、制动踏板位置,同时按照挡位规则进行更换挡位,从而实现3辆卡车的列队行驶,头车起步过程的速度情况如图4所示.图中t为车辆行驶时间；3个坐标点分别为紧急制动分析时的制动位置.

图4　头车车速Fig.4　Velocity of leader truck

2自适应模糊控制算法的建立

2.1控制过程的问题描述

目前应用于车辆控制的算法有很多,例如滑模变结构控制、PID算法、神经网络、最优控制以及模糊控制等等,然而在实际应用中很难建立六轴半挂卡车精确的数学模型,同时当车辆行驶速度较快时,要求控制算法应避免大量运算,具有良好的实时性.而在诸多算法中,模糊控制可以根据系统的输入、输出,凭借经验知识制定模糊规则,不用对系统建立精确的数学模型甚至不需要模型便可实现控制,计算过程简单且更符合人类思维,因此成为了比较合理的选择.

然而传统的模糊控制算法由于无法对输入参数进行实时调节,因此在使用过程中只能适应某段速度下的精确控制,在其他速度下难于实现其油门开度和制动踏板控制的平稳.例如：当车辆低速行驶时,列队行驶车辆的控制过程较为安全,不易发生碰撞,同时由于速度较慢,输出的控制量变化不能过于灵敏,否则容易产生挡位的频繁更换,影响控制效果以及车辆行驶过程中的燃油经济性,因此模糊控制的输入量,即各车辆之间的行驶间距与相对速度参数范围可以适当加大；当车辆速度不断提高,列队行驶车辆控制过程的安全性逐渐降低,输出的控制量变化应及时、准确、有效,否则容易发生事故,因此模糊控制的输入量应适当缩小范围.

针对以上问题,采用自适应的模糊控制算法对控制器的输入量进行有效调节,方法有2种：一种为通过跟随车辆速度对输入量进行适当的调节,此时模糊控制器的输入量将随着车辆速度的增加而缩小控制范围,然而当速度变化较大时控制容易产生较大的阶跃信号,使得控制质量降低；另一种采用基于挡位信息的参数控制,其本质是通过判别当前工况下的车辆挡位,根据挡位设定加权系数,挡位越高则加权系数越小,将该加权系数与模糊控制器的输入量进行相乘,即可通过该方法实现对模糊控制器输入量的自适应调节,同时由于加权系数的改变是在换挡过程中进行的,换挡时没有油门开度与制动踏板的操作,因此即使加权系数变化较大,也不会出现控制信号的振荡或者阶跃,所以采用后者进行自适应模糊控制算法的设计,其基本控制流程如图5所示.图中的参考输入为前车与跟随车辆之间的间距误差和相对速度,通过挡位信息设定输入量的加权系数,与参考输入相乘后进行归一化处理,再对其模糊化后进行模糊推理即模糊规则的制定.将由规则得到的模糊量进行清晰化后输出为车辆油门开度与制动踏板信号,该信号将被提供给被控制对象即跟随车辆完成车辆速度与行驶间距的实时控制.

图5　自适应模糊控制流程图Fig.5　Adaptive fuzzy control diagram

2.2控制器基本参数设计

1)语言值的选取

图6　隶属度函数示意图Fig.6　Membership function map

选取语言值有负大(NB)、负中(NM)、负小(NS)、零(ZE)、正小(PS)、正中(PM)、正大(PB),以输出信号为例,其物理含义为负值代表制动信号,正值为油门信号,大、中、小为信号的强弱程度,如图6所示为输出值论域的语言变量结构中各隶属度函数的分布情况.

2)隶属度函数的设定

隶属度函数采用高斯与双边高斯2种形式实现各语言值在论域上的分布,其中负大、负中、正中、正大采用高斯型,参数形式为[σ,c] ,负小、零、正小采用双边高斯型,参数形式为 [σ1,c1,σ2,c2],具体参数数值如表2所示：

表2　隶属度函数设计参数

3)模糊推理规则及清晰化

算法采用统一的模糊控制规则,内容如表3所示,其中vrel为相对速度变化量,derr为间距误差.当vrel和derr均为NB时,代表跟随车辆比头车速度快很多,同时两车之间间距远远小于参考间距,此时输出信号为NB,即应最大程度地踩制动踏板进行减速,避免发生碰撞.

表3　模糊控制规则表

清晰化采用面积重心法实现,公式如下：

(1)

式中：z为得到的模糊值；μ(z)为z所对应的隶属度函数；z0为清晰化的结果；a、b为边界值.

4)间距误差

算法的输入量为车辆之间间距误差以及相对速度,间距误差的示意图如图7所示及表达式如下：

图7　间距误差示意图Fig.7　Schematic diagram of spacing error

(2)

derr=Δd-dref.

(3)

dref=do+Thvf.

(4)

式中：Δd为实际间距；xL为前车行驶位置；xf为后车行驶位置；L为车身长度；dref为参考间距,其值是随着速度的增加而增加的；do为安全距离,即车辆出现紧急制动时车辆停止后的安全距离,设置为2 m；Th为时间常数；vf,af分别为跟随车辆速度与加速度；vL,aL分别为头车速度与加速度.

3仿真模型及结果

3.1车辆列队行驶仿真模型

通过TruckSim和Matlab联合仿真可以准确地模拟车辆列队行驶过程的控制效果,验证自适应模糊控制算法的可行性和有效性.

图8　列队行驶仿真模型Fig.8　Platooning simulation model

如图8所示为3车列队行驶的仿真模型,其中头车在设定的驾驶工况下行驶,后车进行跟随,在图中s_ss_sss1、s_ss_sss2、s_ss_sss3分别为3辆卡车的代码,该代码代表仿真车辆为六轴半挂卡车.在现实环境中车辆位置和速度数据均可通过GPS、激光雷达或者测速装置测得,并可以通过车联网进行实时传输,那么在仿真中相当于可以得到3车位置信号Pos1、Pos2、Pos3和速度信号Vel1、Vel2、Vel3,此外,仿真模型中的Spd2、Spd3分别为跟随车辆变速箱的输出转速,用以和油门开度确定跟随车辆的挡位Gear2、Gear3,自适应模糊控制器1与自适应模糊控制器2的输出分别为跟随车辆的油门开度信号Thr2和Thr3、制动踏板信号Bra2和Bra3以及挡位,该挡位信号也将决定自适应模糊控制算法输入量的加权系数.

3.2仿真结果

分为2种工况对仿真模型进行分析,1)工况为头车在路况良好的情况下自由行驶,无制动发生；2)头车起步行驶过程中有紧急制动,此时将分析算法对列队行驶车辆的控制情况.

图9　车辆列队仿真结果Fig.9　Platooning trucks simulation results

1)头车无制动工况

车辆间的行驶间距Δd与误差derr、相对速度vrel及加速度a的仿真结果如图9所示,从图9(a)中可以看出行驶间距是随着跟随车辆速度的增加而逐渐增大的,起步过程中行驶间距最大不超过15 m；图(b)中列队行驶车辆之间的间距误差均在0至0.4 m以内,且也呈逐渐增大趋势,说明行驶间距总是略大于参考间距,即无需制动便可完成起动过程；图(c)中车辆之间相对速度在车辆起动后变化范围为-0.25～0.5 m/s,即1 s内变化不会超过0.5 m；从图9(d)中可以看出车辆起动时加速度变化较大,起动后加速度变化平稳,只有换挡时有阶跃或者振荡现象.

如图10所示为跟随车辆的油门开度仿真图形,图中油门开度的起伏原因是由于当挡位变换时油门踏板将抬起,即油门开度为0%.起步过程中由于自适应模糊控制算法有效地实现了对跟随车辆油门开度的控制,使得车辆行驶间距、相对速度以及挡位控制稳定,因此制动踏板并没有得到信号产生制动过程.

图10　油门开度仿真结果Fig.10　Throttle simulation results

2)头车紧急制动工况

以图4工况作为头车工况,当头车速度为6、11、17 m/s时进行紧急制动的仿真实验,其制动开始时间分别为第72、123、156 s,分别定义为制动工况1、制动工况2、制动工况3.所使用列队行驶车辆均为同一车辆模型,即在实际车队组建中为保证紧急制动时车辆具有良好的制动效果,提高车队的安全性,应选择同一类车型组建车队.紧急制动的仿真结果如图11所示,从图11(a)中可以看出头车在6 m/s制动时,当车队停止时,头车与中间车辆之间间距为5.51 m,中间车辆与尾车之间间距为5.63 m；在11 m/s制动时(图(b)),间距分别为7.29和5.11 m；在17 m/s制动时(图(c)),间距分别为11.24和8.89 m.制动过程无碰撞事故发生,同时由于在TruckSim模型中已设置有ABS参数,有效地控制滑移率在0.1至0.2之间,因此也无甩尾、侧翻等现象发生.

图11　制动仿真结果Fig.11　Brake simulation results

4结论

(1)为了得到实际换挡规律,在6名驾驶员驾驶12挡商用车行驶3.5万公里的实验数据中提取了起步过程中的挡位数据并进行了统计分析,可以发现驾驶员一般在起步过程中不采用逐级换挡,其中3挡至6挡、11挡使用概率很小.

(2)通过分析车辆的实际换挡规律,建立了3车纵向列队行驶的自适应模糊控制模型,在TruckSim和Matlab联合仿真中模拟了起步行驶的控制过程.

(3)仿真结果表明：在180 s内三车挡位均升至最高挡,速度达到74 km/h；在起步过程中行驶间距最大不超过15 m,间距误差控制在5 %以内；在起步过程中跟随车辆油门开度控制平稳；在头车紧急制动时,车队停止后车辆之间可以保持一定的安全距离.

参考文献(References)：

[1] 中华人民共和国国家统计局. 2014年国民经济和社会发展统计公报 [EB/OL]. (2015-02-26) [2015-09-27]. http:∥www.stats.gov.cn/tjsj/zxfb/201502/t20150226_685799.html．

[2] 中华人民共和国交通运输部. 2014年交通运输行业发展统计公报 [EB/OL]. (2015-07-23) [2015-09-27]. http:∥www.mot.gov.cn/zhuzhan/jiaotonggaikuang/201507/t20150723_1853384.html．[3] NIEUWENHUIJZE M R I, KEULEN T V,ÖNCÜ S, et al. Cooperative driving with a heavy-duty truck in mixed traffic: experimental results [J]. Transactions on Intelligent Transportation Systems, 2012, 13(3): 1026-1032.[4] TSUGAWA S, KATO S, AOKI K. An automated truck platoon for energy saving [C]∥ Intelligent Robots and Systems. San Francisco, USA: [s. n.],2011:4109-411．

[5] FRANKE U, BÖTTIGER F, et al. Truck platooning in mixed traffic [C]∥ Proc. of the Intelligent Vehicle Symposium. Detroit, USA: [s. n.] ,1995:1-6．

[6] GEHRIG S K, STEIN F J. Collision avoidance for vehicle-following systems [J]. Intelligent Transportation Systems, 2007.5(4):112-120．

[7] GEHRING O, FRITZ H. Practical results of a longitudinal control concept for truck platooning with vehicle to vehicle communication [C]∥ Intelligent Transportation System. Boston, USA: [s. n.] , 1997:117-122．

[8] VINEL A, LIN L , LYAMIN N. Vehicle-to-vehicle communication in c-acc/platooning scenarios [J] . Communications Magazine, 2015,53(8):192-197．

[9] TSUGAWA S, KATO S.Energy ITS: another application of vehicular communications [J]. Communications Magazine, 2010,48(11)120-126．

[10] 马育林,吴青,张蕊,等. 模拟自治车队行驶过程变工况速度跟踪控制[J]. 机械工程学报,2011,47(7):140-147．

MA Yu-lin, WU Qing, ZHANG Rui, et al. Speed tracking control for a simulated intelligent vehicle platoon under variable road conditions [J]. Journal of Mechanical Engineering, 2011,47(7):140-147．

[11] 高振海, 吴涛, 尤洋. 基于粒子群算法的汽车自适应巡航控制器设计[J]. 农业机械学报, 2013,44(12):11-16.

GAO Zhen-hai, WU Tao, YOU Yang. Design of vehicle adaptive cruise controller based on PSO algorithm [J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(12):11-16.

[12] 岳伟,郭戈. 自主车队的非线性建模与控制[J]. 控制与决策,2009,24(7):996-1000.

YUE Wei, GUO Ge. Nonlinear modelling and control of autonomous platoon [J]. Control and Decision, 2009,24(7):996-1000.

[13] 任殿波, 张策, 张继业.考虑前后信息的车辆跟随自适应控制[J]. 哈尔滨工业大学学报. 2011, 43(6):76-80.

REN Dian-bo, ZHANG Ce, ZHANG Ji-ye. Vehicle following adaptive control using front and back information [J]. Journal of Harbin Institute of Technology, 2011,43(6):76-80.

第50卷第5期2016年5月浙 江 大 学 学 报(工学版)JournalofZhejiangUniversity(EngineeringScience)Vol.50No.5May2016

Starting control of platooning trucks based on actual gearshift schedule

LI Ming-da1,2,KUI Hai-lin1,MEN Yu-zhuo2,BAO Cui-zhu1

(1.CollegeofTransportation,JilinUniversity,Changchun130022,China；2.SchoolofMechatronicsEngineering,ChangchunInstituteofTechnology,Changchun130012,China)

Abstract:456 segments gear status data in the start process were extracted from the experiment vehicle traveling 35,000 kilometers in order to solve the starting control problem of platooning trucks.The corresponding gearshift rule was developed with the statistics and analysis.The control model of vehicle platoon was established by using adaptive fuzzy control algorithm. The weight coefficients were decided through the gear status information of the following vehicle. They were used to adjust the input scale of fuzzy controller in order to improve the adaptability of control algorithm. Through co-simulation of TruckSim and Matlab, three trucks platoon was simulated in the case of vehicle-vehicle communication environment using the test data from real vehicle as the simulation conditions of the leader truck. The simulation results show that the travel space error between two vehicles can be controlled within 5 percent of driving distance in unit time. The control model has certain control accuracy.

Key words:gearshift rule; adaptive fuzzy control; platoon ; TruckSim；Matlab；co-simulation

收稿日期：2015-09-27.浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng

基金项目：国家自然科学基金资助项目(51378075).

作者简介：李明达(1982-)，男，博士生，讲师，从事车路协同节能技术等研究.ORCID : 0000-0002-1127-9305.E-mail:limingda_123@qq.com通信联系人：隗海林，男，教授，博导．ORCID ：0000-0002-1365-0980.E-mail:khl69@163.com

DOI:10.3785/j.issn.1008-973X.2016.05.011

中图分类号：U 491

文献标志码：A

文章编号：1008-973X(2016)05-0887-06