颗粒粒径对岩崩碎屑流对挡板冲击影响

孙新坡，何思明，樊晓一，田述军，张玲玲，田文高

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.中国科学院水利部 成都山地灾害与环境研究所，四川 成都 610041)



颗粒粒径对岩崩碎屑流对挡板冲击影响

孙新坡1，何思明2，樊晓一1，田述军1，张玲玲1，田文高1

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.中国科学院水利部 成都山地灾害与环境研究所，四川 成都 610041)

摘要：调查颗粒之间的相互作用及岩崩碎屑流和一个障碍之间相互作用.采用光滑粒子流体动力学法(SPH)来模拟实验中观察到的颗粒流动规律，采用的本构模型是牛顿流体模型.研究表明：粒径大小对颗粒运动以及与结构的冲击力有很大的影响，粒径为8，12，14 mm时的应力云图类似，挡板两侧为应力集中部位，粒径为10 mm时的应力较均匀，近似为矩形分布，在挡板中央部位.获得了一些重要的模型参数，可以用于优化在高山地区防御结构的设计.

关键词：岩崩碎屑流；牛顿流体；挡板；粘度；SPH

震后，在中国西南地区的灾害及次生灾害，造成经济和人员伤亡.岩崩碎屑流与构筑物相互作用是问题重点，研究工作还比较少.Chehata等[1]实验研究了密集的颗粒状材料绕浸在其中的圆柱体流动特性，主要关注圆柱体上的阻力.Chiou[2]通过一系列的实验研究了颗粒物质在障碍物周围的沉积行为和流动区域.Chjeng-Lun SHIEH等[3]采用流体动力学方法研究了碎屑流作用在曲面坝上的作用力，并与室内水槽模型试验进行了对比.何思明等[4]以都汶公路彻底关大桥为依托研发一种新型桥墩抗滚石冲击垫层结构，并采用非线性有限元对桥墩受滚石撞击过程进行数值模拟研究.吴永等[5]以水文学为基础，研究作用在单元条块堆积体上静水压力和动水压力的计算方法.乔建平等[6]采用危险指数法建立了滑坡危害性分区标准.黄润秋和许强等[7-8]针对典型滑坡进行了深入、系统地分析研究.杨伟等[9]采用ARCGIS集成的VBA开发环境，提出了一种三维折线法分析边坡的稳定性.孙新坡等[10]采用离散元法对崩塌体在地震作用下动力破碎过程进行了模拟.李磊等[11]采用有限元软件LS-DYNA中的SPH算法实现聚能装药射流形成过程的三维数值模拟.

以水槽流砂试验为研究对象，运用SPH法进行数值分析对岩崩碎屑流运动以及受挡板作用滑动和堆积，并与实验结果进行对比，得出合理的力学参数，用作岩崩碎屑流方面的防治.

1建模及分析

1.1问题描述

彻底关大桥位于国道213线都(江堰)-汶(川)公路K44+235处，地震时被崩塌滚石毁坏后，2009年5月12日重建.由于连日大雨，2009年7月25日再次发生大面积崩塌，导致桥墩再次被毁坏[4]，如图1所示.

图1　彻底关大桥附近的岩崩碎屑流Fig.1　The rockfall debris flow near Chediguan bridge

为了研究岩崩碎屑流的动力运动机理及与结构物相互作用，构建了一个理想模型，半球形的岩崩碎屑流在重力作用下沿一个倾斜的水槽流动以及和一个障碍物挡板相互作用.通过比较计算结果与一些基准实验来确定所需参数.Chiou[2]的模型测试报告非常适合我们所进行的研究.实验室模型试验相比实地测量的岩崩碎屑流有许多优势.在实验室测试中，通过设定明确的初始和边界条件可以很好的再现测试结果.实验室水槽实验的另一个优点是可以改变地貌倾角、挡板的位置和尺寸.地形对颗粒流动和沉积的影响可以通过改变研究挡板位置和水槽倾角来实现.同样，颗粒材料的类型、数量和初始流动形状可以很容易地由实验室岩崩碎屑流实验来控制.

水槽的截面几何模型试验[2]，如图2所示.槽分为三个部分:上部倾斜区域，相对于圆形过渡区和水平流动区域.水槽上面倾斜部分的倾角ζ可以调整到30°，40°，45°，50°.水槽平面的总长度1 915 mm，槽宽度约1 100 mm.表1为水槽几何参数.

图2　岩崩碎屑流剖面示意图Fig.2　Cross section of the rockfall debris flow

mm

挡板(长方体)安装在槽倾斜区(图1).显然，与挡板的碰撞的颗粒速度取决于障碍的位置.出于这个原因，考虑了两个挡板位置，即P1=650 mm和P2=810 mm(图2).为了获得对称流模式，大坝是放置在槽的中心.研究了三种挡板的高度，采用表2中给出的尺寸.

表2　挡板几何参数

颗粒材料的特点是：密度、恢复系数和内摩擦角，基底摩擦角度.Chiou[2]采用的是粗石英砂，平均直径5 mm，材料密度2 650 kg / m3和恢复系数约为0.75.

1.2基本理论

SPH方法[11]是通过构造一个核函数对离散质点进行计算的.

常用的核函数有B-spline核函数、Gauss核函数、二次核函数及指数核函数等，其中B-spline核函数是目前应用最广泛的核函数，其形式[12]为

(1)

Mie-Grüneisen状态方程的耗能是线性的，通用方程为

P-PH=Γρ(Em-EH)

(2)

其中：PH和EH分别为Hugoniot压力和比能；Γ为Grüneisen比定义，即

(3)

式中：Γ0为材料常数；ρ0为参考密度.

Hugoniot能EH，与Hugoniot压力有关，即

(4)

式中η=1-ρ0/ρ是体积压缩应变.由式(4)消除Γ和EH得到

(5)

线性Us—UpHugoniot形式中Hugoniot通用形式为

(6)

c0和s定义冲击波速度Us和粒子速度Up的线性关系，s为无量纲，表示为

Us=c0+sUP

(7)

上面假设的Us-UpHugoniot形式为

(8)

牛顿内摩擦定律表达式为

τ=μγ

(9)

式中：τ为所加的切应力；γ为剪切速率； μ为黏度.

1.3SPH数值建模

不失为一般性，根据实验室的水槽试验的实际尺寸，构建数值模型见图3.

在数值模型中，岩崩体为半球形，由SPH质点粒子模拟，挡板由刚性墙模拟，如图3所示.岩崩体由质点粒子模拟，滑动面用刚性“壳单元”模拟.岩崩体体积为0.002 1 m3，建立4种不同粒径大小的模型，采用质点虚拟半径范围4，5，6，7 mm.总颗粒数分别为8 574，4 203，2 119，1 409个.实际岩崩碎屑流的成分、颗粒粒径和级配复杂，而模型试验采用单一流砂来模拟实际碎屑流，其真实性如何，有待与实际崩塌碎屑流结果对比.

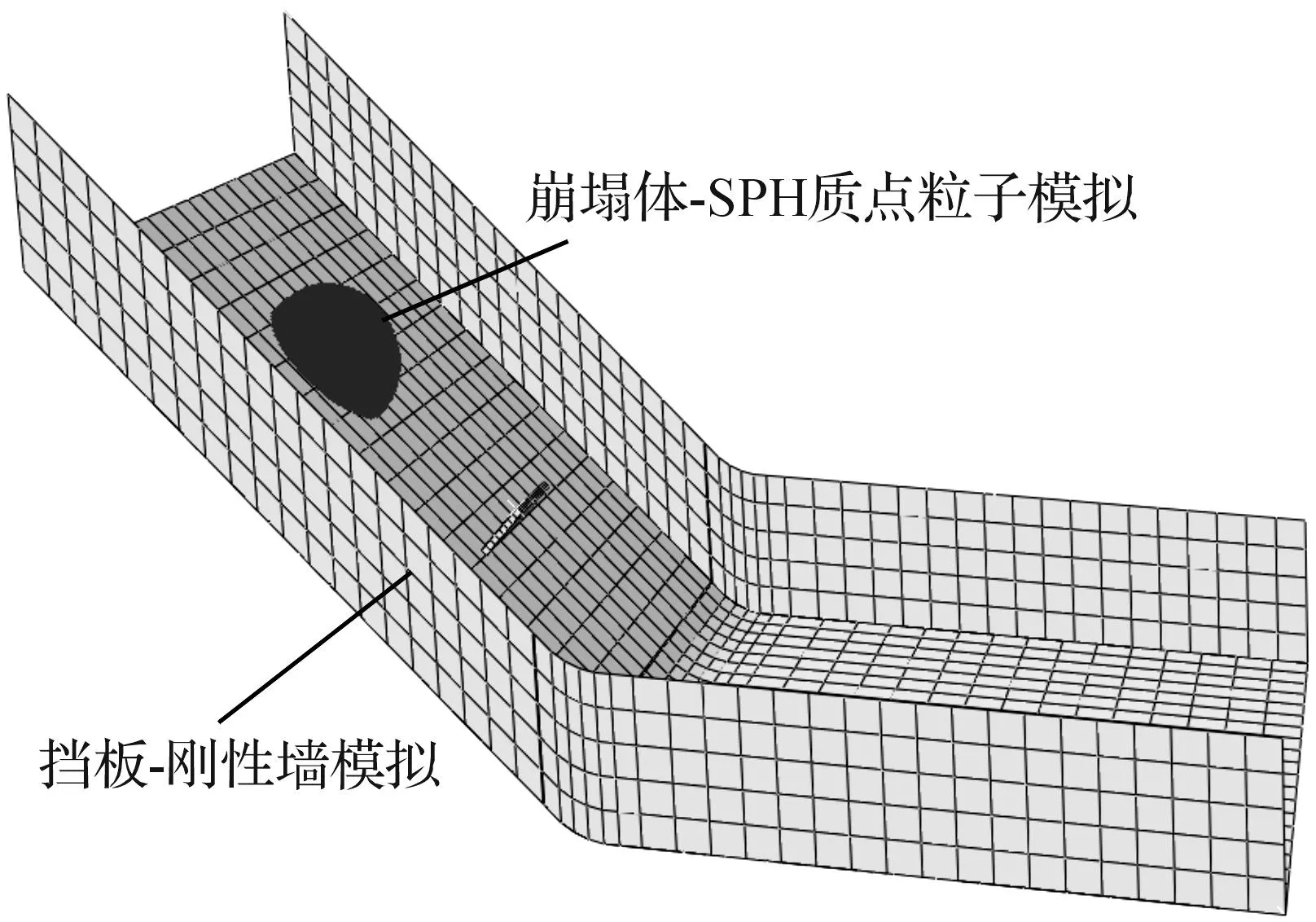
图3　岩崩碎屑流与挡板数值模型Fig.3　Numerical model of rockfall debris flow and dam

1.4参数确定

通过进行大量参数试验，选择了一组与试验符合的比较合理的参数作为计算参数.表3为模拟采用的砂的参数.

表3　砂的参数

2计算结果与实验对比分析

现在对水槽的不同倾角的岩崩体的堆积形态和速度场进行分析.

2.1水槽倾角40°时计算结果分析

图4显示了SPH仿真和实验的颗粒堆被释放后在不同的时间的一些快照.水槽倾角40°，挡板在P1.图4(a)t=0.28 s,图4(b)t=0.56 s,图4(c)t=0.84 s, 图4(d)t=8.2 s.快照是在同一次SPH计算和实验同时刻拍的照片.目测仿真和实验的流场结果对比比较吻合.大约17.5%的颗粒质量被挡墙阻挡.数值模拟是非常接近实验结果，误差±1.5%.SPH方法可以获得颗粒流在斜带和沉积的主要特点.

图4(c)显示更多的颗粒流实验中心以外的障碍.我们认为这是由于挡板边缘粒子的干扰.有角的粒子比球形粒子的干扰更明显.图4(d)也证实了这一点.计算结果显示挡板后面中线上颗粒少于实验结果.

图4　岩崩体滑动演化过程SPH数值模拟(左)与试验(右)对比分析Fig.4　Flow-obstacle interaction: comparison between the SPH simulation (left panels) and the laboratory experiment (right panels)

2.2岩崩体滑动过程中的速度场分析

速度场的模拟和实验的对比，如图5所示.实验采用PIV(粒子图像测速技术) 测量表面速度.一些颗粒被挡板阻挡在挡板前形成静态区.静态区的颗粒数量随着时间的推移而增加，直到达到静止状态.图5中颗粒流被挡板分成两个分支.比较PIV测量和SPH模拟显示了速度场比较吻合.挡板前的静态区的模拟细节非常重要，因为防护结构的设计依赖于颗粒与挡板的动态碰撞和挡板前的颗粒的质量.岩崩防护的一个关键问题在于保护是低于围护结构的保护区域.SPH模型能够模拟挡板下面的保护区域.通过速度云图5可看出速度最大的粒子分布在尾部和两侧.

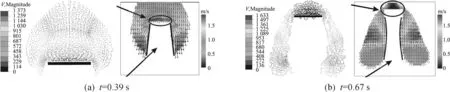
图5　SPH数值模拟与试验对比分析Fig.5　Particle velocities in the SPH calculation (left panels) (mm/s) and in the experiment (right panels)

由图6可知：不同粒径颗粒在运动3.9 s和6.7 s的最大颗粒运动速度差值，随着粒径增大，到粒径为12 mm时，差值先增大到最大，之后减小.

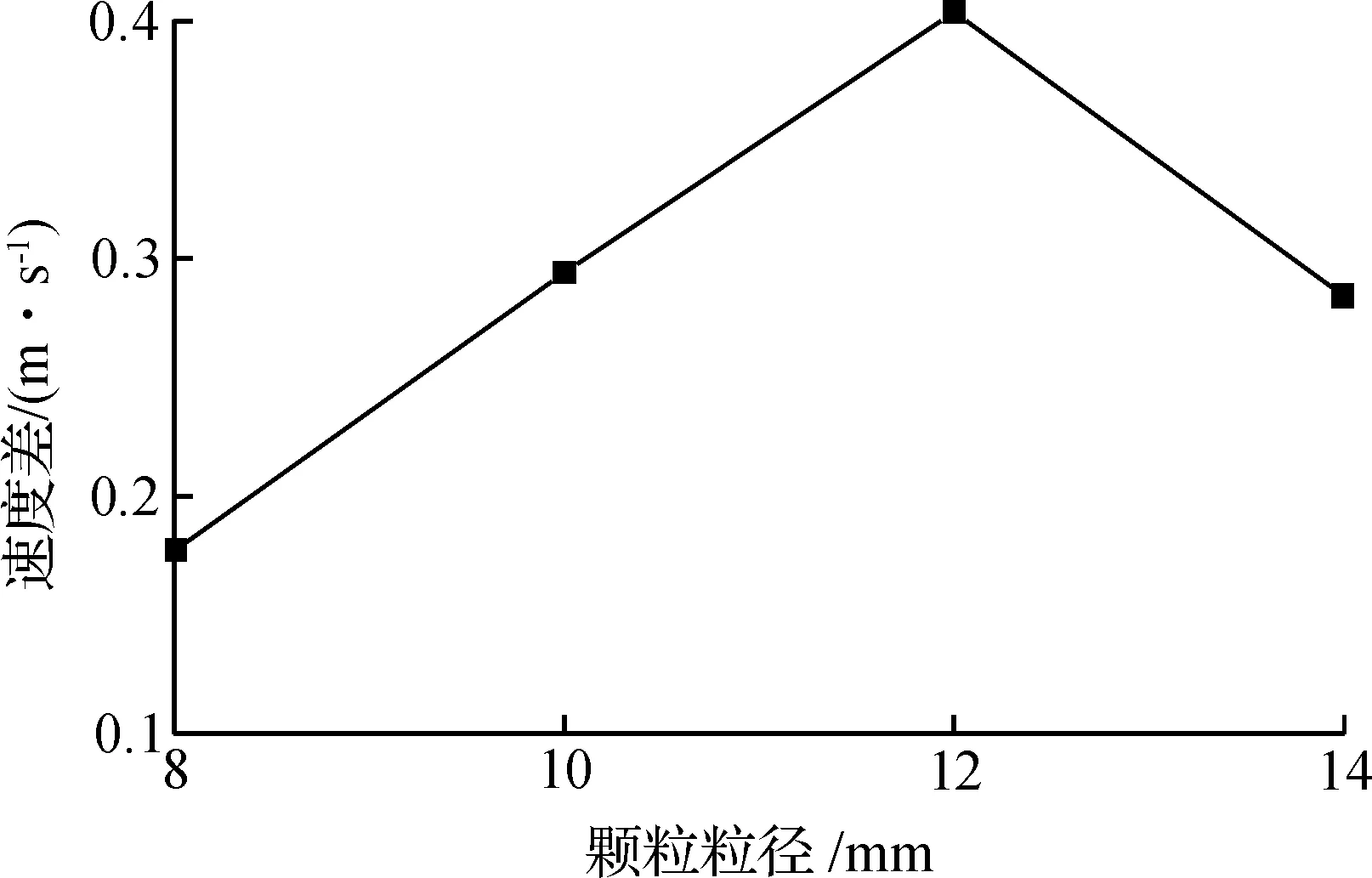
图6　不同水槽倾角岩崩体滑动速度差值图Fig.6　Different tank inclination of rockfall debris sliding velocity difference

2.3不同颗粒直径大小对冲击力的影响

图7为不同粒径大小的挡板冲击力时程曲线，粒径大小分别为8，10，12，14 mm，到达挡板时间都是0.308 s.由图7可看出粒径大小对冲击力的时程曲线有重要的影响.

图7　挡板高80 mm时的冲击力的时程曲线Fig.7　Time histories of impact force (the height of dam 80mm)

图8为不同粒径大小对最大冲击力的影响，随着粒径的增长，最大冲击力的值增大，之后随着粒径的增长，最大冲击力的值逐渐减小.

图9为不同粒径岩崩达到挡板的最大冲击力的所需时间，粒径8～10 mm时，所需时间减小，之后，10～12 mm时，到最大冲击力时间增大，12～14 mm的最大冲击力时间相等.

图8　不同挡板的最大冲击力的时程曲线Fig.8　Time histories of impact force for different dam heights

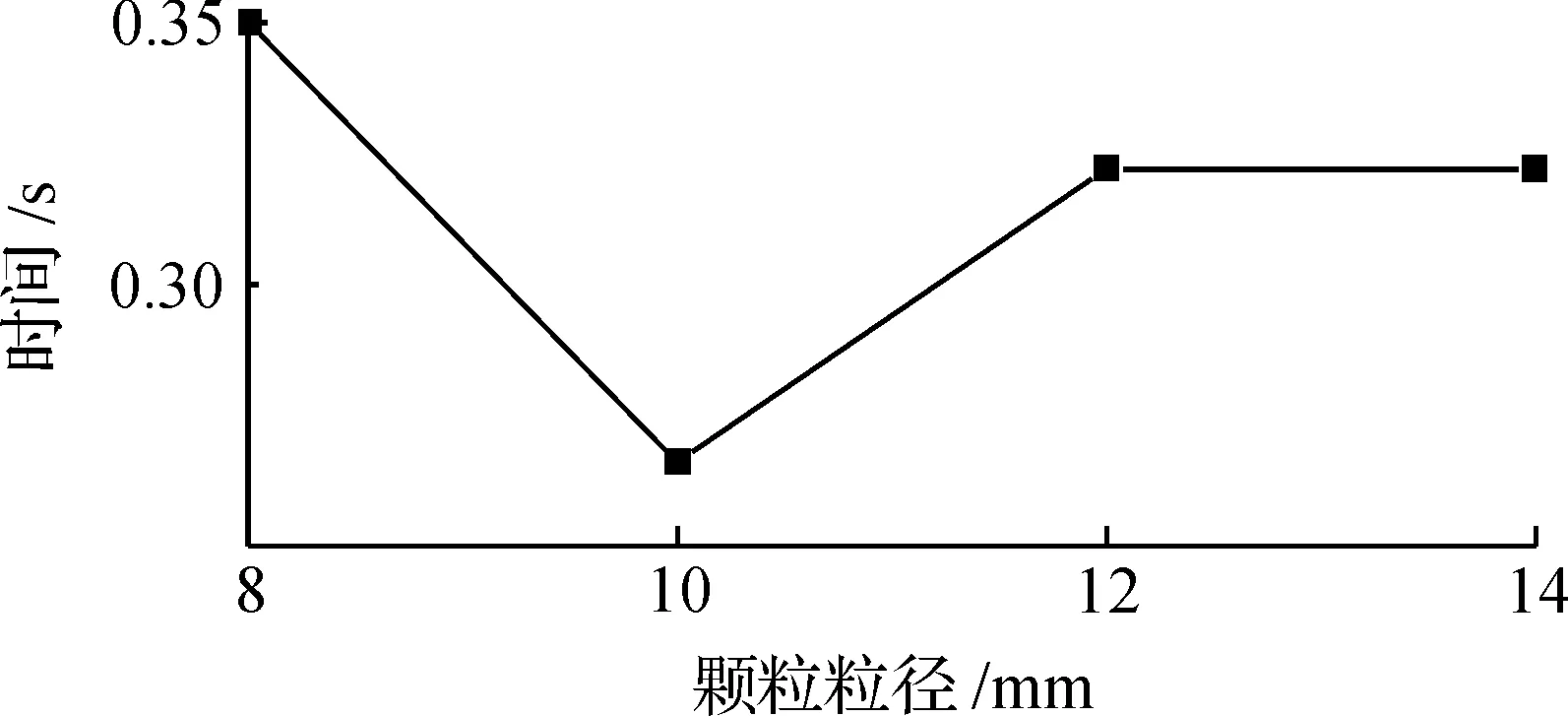
图9　不同粒径岩崩达到挡板的最大冲击力的所需时间Fig.9　Time histories of impact force for different dam heights

2.4不同颗粒直径大小对应最大冲击力时的受力分析

图10为不同粒径的最大冲击力时的应力云图，由图10可以看出：图10(a)粒径最小，所需颗粒最多，所以指点最密集，随着粒径增大，所需颗粒越少，越稀疏，粒径为8，12，14 mm时的应力云图类似，挡板两侧为应力集中部位，粒径为10 mm时的应力较均匀，近似为矩形分布，在挡板中央部位.

2.5不同颗粒直径大小对应最大冲击力时的速度分析

图11为不同粒径的最大冲击力时的速度云图，由图11可以看出：粒径越大，颗粒最少，越稀疏.粒径为8，12，14 mm时的应力云图类似，挡板两侧为应力集中部位，粒径为10 mm时的应力较均匀，近似为矩形分布，在挡板中央部位.

图10　挡板冲击力最大时应力云图Fig.10　Stress nephogram while impact reach max

图11　挡板冲击力最大时速度云图Fig.11　Velocity nephogram while impact reach max

3结论

通过SPH方法模拟岩崩与试验对比分析，结果表明了SPH法可以模拟颗粒物质流动以及颗粒和结构之间的相互作用；模拟结果与实验进行了比较，结果显示仿真和实验结果比较吻合.颗粒的分散特性是由数值模拟与实验拟合得到；岩崩碎屑流的运动和堆积及与结构冲击力受到颗粒粒径大小的影响；不同粒径颗粒在两个不同时刻的速度差值先增大到极值，后降低；最大冲击力随着粒径增大到10 mm，流动机制受挡板的位置以及高度的影响，不同位置和不同高度的挡板前颗粒堆积以及挡板后保护区范围和形态不同，可以计算挡板阻挡的颗粒大小以及受挡板影响的保护区域的动态变化范围.

本文得到西南科技大学博士基金项目(12zx7124)的资助.

参考文献：

[1]CHEHATA D, ZENIT R, WASSGREN C R. Dense granular flowaround an immersed cylinder[J]. Physics of fluids，2003,15(6):1622-1631.

[2]CHIOU M C. Modelling dry granular avalanches past different obstructs： numerical simulations and laboratory analyses, dissertation[D]. Darmstadt： Technical University Darmstadt，2005.

[3]SHIEH C L，TING C H，PAN H G. Impulsive force of debris flow on a curved dam[J].International journal of sediment research，2008，23(2)：149-158.

[4]何思明，庒卫林，张雄，等.都汶公路彻底关大桥桥墩抗滚石冲击防护研究[J].岩石力学与工程学报，2013，32(增2)：3421-3427.

[5]吴永，何思明，裴向军，等.震后沟道泥石流启动条件——松散堆积体雨中失稳的水力学机制分析[J].山地学报，2012，33(10)：3043-3050.

[6]乔建平，田宏岭，石莉莉，等.采用危险指数法研究达县特大型暴雨滑坡发育特征[J].山地学报，2008，26(6)：739-744.

[7]黄润秋，许强.中国典型灾难性滑坡[M].北京：科学出版社，2008.

[8]许强，黄润秋.汶川大地震诱发崩塌灾害动力特征初探[J].工程地质学报，2008，16(6)：721-729.

[9]杨伟，丁伯阳，潘晓东，等.基于GIS的边坡三维稳定性计算[J].浙江工业大学学报，2012，40(1)：92-95.

[10]孙新坡,何思明,于忆骅.基于离散元法崩塌体动力破碎分析[J].浙江工业大学学报,2015，43(4):464-467.

[11]李磊，沈兆武，李学岭，等.SPH方法在聚能装药射流三维数值模拟中的应用[J].爆炸与冲击，2012，32(3)：316-322.

[12]CHOU P C, CARLEONE J, FLIS W J, et al. Improved formulas for velocity, acceleration, and projection angle of explosively driven liners[J]. Properllants, explosives, pyrotechnics,1983,8(6):175-183.

(责任编辑：陈石平)

The effect of particle size on the impact of rockfall debris on obstacles

SUN Xinpo1, HE Siming2, FAN Xiaoyi1, TIAN Shujun1, ZHANG Lingling1, TIAN Wengao1

(1.College of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang, 621010, China;2.Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China)

Abstract:The interactions between particles and between the rapid rockfall debris flow and obstacles are investigated. Smooth particle hydrodynamics (SPH) with the Newtonian fluid contact model is used to simulate the flow regimes observed in laboratory experiments. It is shown that the particle size has a great influence on particle movements and on the impact on structures. When the particle size is 8, 12, and 14 mm, the stress nephograms are similar and stress concentrations occur on both sides of the obstacle. When the particle size is 10 mm, the stress distribution is comparatively uniform and approximately in a rectangular form in the central region of the obstacle. Some important model parameters are obtained, which can be used to optimize defense structures in mountain regions.

Keywords:rockfall debris flow; Newtonian fluid; obstacle; viscosity; SPH

收稿日期：2015-10-13

基金项目：国家自然科学基金资助项目(41472325，41272297,41401195)；绵阳市科技局资助项目(14S-02-5)

作者简介：孙新坡(1978―)，男，河北保定人，讲师，博士，主要从事山地灾害形成机理及防治技术研究，E-mail：xinpo2008@sina.com.cn.

中图分类号：X43

文献标志码：A

文章编号：1006-4303(2016)02-0221-05