基于ABAQUS软件的RC Z形柱框架节点仿真分析

崔钦淑，倪振强

(浙江工业大学 建筑工程学院，浙江 杭州 310014)



基于ABAQUS软件的RC Z形柱框架节点仿真分析

崔钦淑，倪振强

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

摘要：混凝土损伤塑性模型是有限元分析软件ABAQUS中的一种材料模型,能够较好的描述混凝土的材料特性，运用ABAQUS软件提供的混凝土损伤塑性模型参数与Sidiroff提出的能量等价原理结合起来推导出损伤因子的计算式，这种损伤塑性模型具有较高的模拟精度，可用于实际复杂混凝土构件的设计与分析.用ABAQUS对Z形柱框架节点进行仿真分析，混凝土本构关系分别采用规范中的表达式和Hongnestad表达式，得到混凝土等效塑性应变云图，将节点荷载-位移骨架曲线与试验结果进行对比，给出黏性系数的最佳取值范围，可为工程应用提供参考.

关键词：RC Z形柱；框架节点；损伤因子；非线性有限元分析；ABAQUS

一般常采用试验和数值模拟方法来研究RC异形柱框架节点的受力和变形性能，崔钦淑等[1]进行了8榀Z形柱中间层节点的抗震试验，朱振华等[2]研究了Z形柱节点在轴压比不同时的抗剪性能，杨俊杰等[3]研究了翼缘长和梁高比值对Z形柱节点抗震性能的影响，傅剑平等[4]对异形柱框架中间层端节点抗震性能进行了试验，试验研究直观，数据可靠，但是费用高，试验周期长并且受实验室试验条件影响大,有限元分析软件强大的非线性分析能力可以解决这些问题.马乐为等[5]进行了T形柱框架节点受剪承载力的非线性有限元分析，季青等[6]通过ANSYS对低周反复水平荷载作用下Z形截面柱受力性能进行数值模拟分析.混凝土塑性损伤模型能较好的描述混凝土在往复荷载作用下的力学特性,结合Sidoroff[7]提出的能量等价原理给出了损伤因子的计算方法并验证了该损伤塑性模型在Z形截面柱节点仿真分析中的有效性.通过改变黏性系数来减少由于试件中钢筋在往复荷载作用下产生的滑移对仿真结果的影响，并给出黏性系数最佳取值范围.

1损伤因子推导

迄今为止，混凝土本构模型理论应用较广，如GB 50010—2010《混凝土结构设计规范》附录C的公式[8]、Hongnestad表达式[9]、美国学者Kent-Park建议公式[10]等，这些本构模型有各自的优缺点及适用范围，但是没有一种理论可以完全描述混凝土的本构关系，混凝土的应力-应变曲线存在下降段,当应力达到峰值后会发生刚度退化,这是由于有微小的裂缝出现在混凝土内部造成的.ABAQUS软件中的混凝土损伤塑性模型是依据Lubliner Lee和Fenves提出的损伤塑性模型确定的,主要用于描述损伤引起的且不可恢复的材料退化特性.引入损伤因子的概念，使ABAQUS软件可以更准确的模拟混凝土在往复荷载作用下的刚度退化特性，从而使仿真结果更准确.

Sidiroff能量等价原理[7]认为有损材料弹性余能与无损材料弹性余能两者具有相同的形式，Cauchy应力张量可以替换为有效应力张量并可用损伤等效模量代替弹性模量.

σ=E0(1-d)2ε

(1)

规范[8]给出的混凝土单轴受压的本构公式为

σ=(1-dc)Ecε

(2)

通过式(1，2)得到混凝土单轴受压的损伤因子计算式为

(3)

同理，可得混凝土受拉损伤因子的计算式为

(4)

式中：σ为应力；ε为应变；E0为原点切线模量；Ec为混凝土的弹性模量；dc为混凝土单轴受压损伤演化参数；dt为混凝土单轴受拉损伤演化参数.

2塑性损伤模型法则

2.1滞回规则

在ABAQUS中，规定受拉刚度恢复系数ωt和受压刚度恢复系数ωc分别为0和1，即混凝土在往复荷载作用下的受压刚度能够恢复而受拉刚度不能够恢复.经过大量的混凝土试验发现，当混凝土从拉应变变成压应变时，由于微小的裂缝重新闭合，混凝土的刚度将会恢复；当从压应变变成拉应变时，由于微小的裂缝被压碎，混凝土的刚度不会恢复[11].其单轴应力循环曲线如图1所示.

图1　单轴应力循环曲线图Fig.1　Uniaxial stress circular curve

2.2屈服准则

混凝土受到的应力比较复杂时，确定混凝土某一点发生塑性变形必须满足公式

(5)

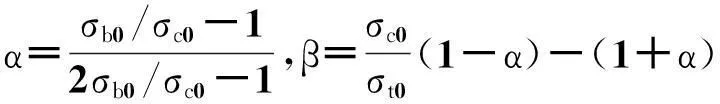
式中：I1为应力张量第一不变量；J2为偏应力张量第二不变量；σb0，σc0，σt0分别为混凝土双轴抗压强度、单轴抗压强度和单轴抗拉强度；Kc为控制混凝土屈服面在偏平面上的投影形状的参数，对于正常配筋的混凝土建议Kc=0.666 7，双单轴受压强度比fb0/fc0=1.16，混凝土初始屈服应力取1/3fc.

2.3流动法则

ABAQUS中的塑性损伤模型流动法则为非关联法则[11]，其塑性势函数为

(6)

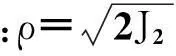
3RC Z形柱框架节点仿真分析

3.1模型参数

仿真对象为文献[1]中的JD2(表1)，钢筋的本构关系采用GB 50010—2010《混凝土结构设计规范》附录C[10]的公式.基于上述损伤因子的计算方法,得到混凝土的受压损伤因子Dc和受拉损伤因子Dt,混凝土真实应力—塑性应变关系曲线，如图2所示.钢筋骨架及Z形柱节点模型如图3所示.钢筋和混凝土采用分离式建模，并用Embed技术对两者的自由度进行耦合，梁柱纵筋及箍筋采用桁架单元T3D2，混凝土及垫块采用实体单元C3D8R.节点核心区单元尺寸为30 mm，其他单元尺寸为50 mm.表1中：ρs与ρc分别为钢筋和混凝土的泊松比；Kc为拉压第二应力不变量比；μ为黏性系数.

模型柱底截面对x，y，z方向位移进行约束，对x，z方向转角进行约束，即U1=U2=U3=UR1=UR3=0，柱顶截面处U1=U2=UR1=UR3=0.在柱顶施加大小为260 kN的轴向荷载，在梁两端同步施加低周往复荷载.在柱支座及梁端设置刚性垫块，是为了避免混凝土局部应力集中引起受压破坏.

表1　模型参数

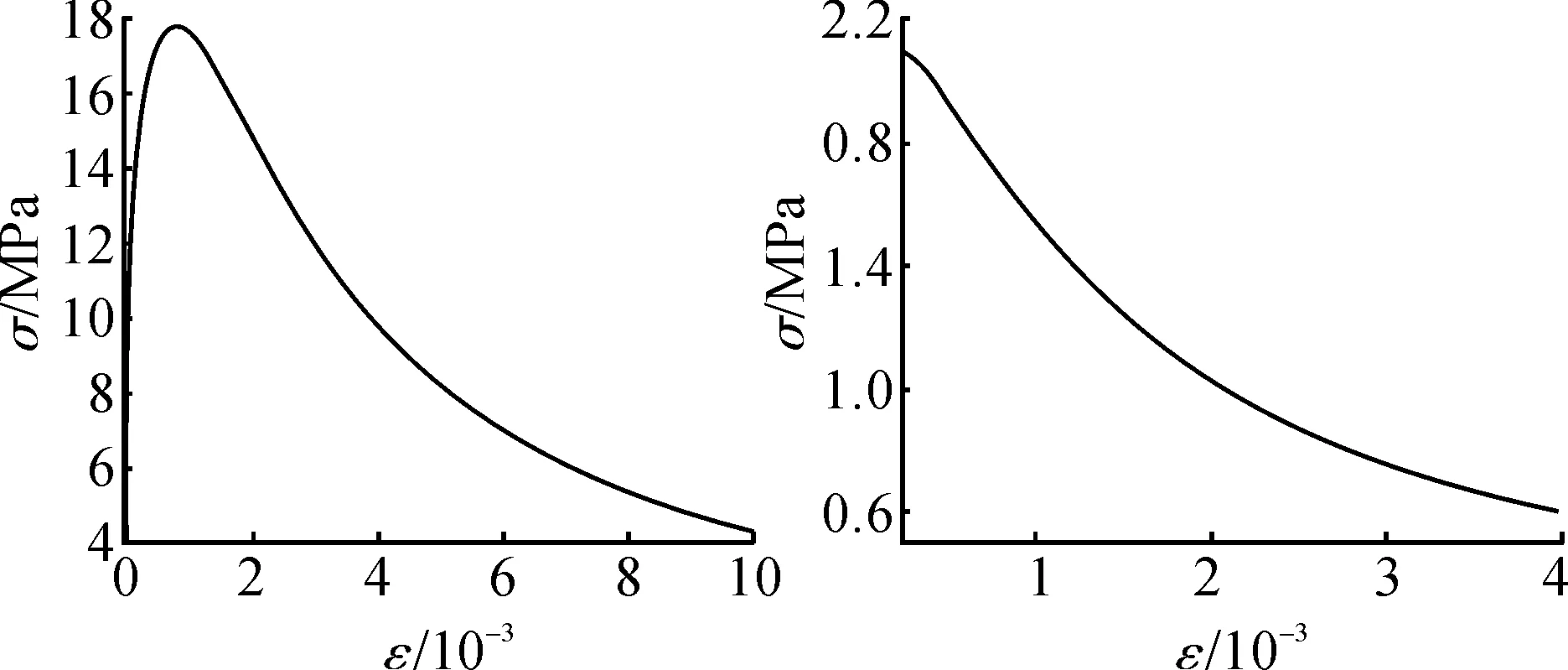
图2　混凝土真实应力—塑性应变关系曲线Fig.2　Real concrete stress-plastic strain curve

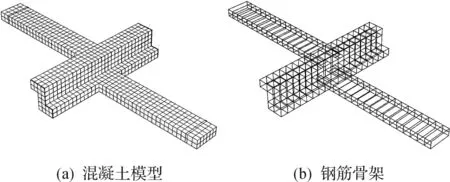
图3　有限元模型Fig.3　Finite element model

3.2后处理结果

ABAQUS仿真得到的梁端荷载—位移骨架曲线与试验得到的骨架曲线进行对比，结果如图4所示.从图4中可看出：《混凝土结构设计规范》附录C的混凝土本构模型的仿真结果骨架曲线要较Hongnestad的混凝土本构模型更接近于试验骨架曲线，同时骨架曲线的趋势与试验骨架曲线相近，说明《混凝土结构设计规范》附录C[8]中的本构模型可以更好的模拟Z形柱框架节点中混凝土的受力性能.

钢筋和混凝土这两种材料能够共同工作的基础是他们之间有足够的黏结力，经过多次仿真分析发现混凝土与钢筋之间的黏性系数也会对结果产生影响.取特征黏性系数进行对比说明，图5表示取黏性系数为0.000 1，0.001，0.005时的梁端荷载-位移骨架曲线与试验骨架曲线的对比，当混凝土与钢筋之间的黏性系数取0.000 5～0.001时，仿真结果与试验结果相差较大；当黏性系数取0.000 1～0.000 5时，仿真结果与试验结果较为接近.

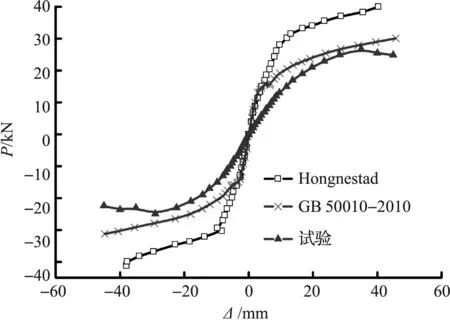
图4　骨架曲线对比图Fig.4　Skeleton curve comparison

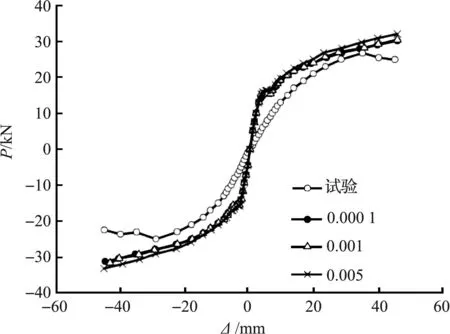
图5　黏性系数不同的骨架曲线对比Fig.5　Skeleton curve with different viscosity coefficients

从图6中可以看出：混凝土在极限荷载作用下的受压损伤情况，柱子几乎没有塑性变形，节点核芯区与梁端的塑性变形比较严重，与现场照片图7的节点破坏情况非常吻合.

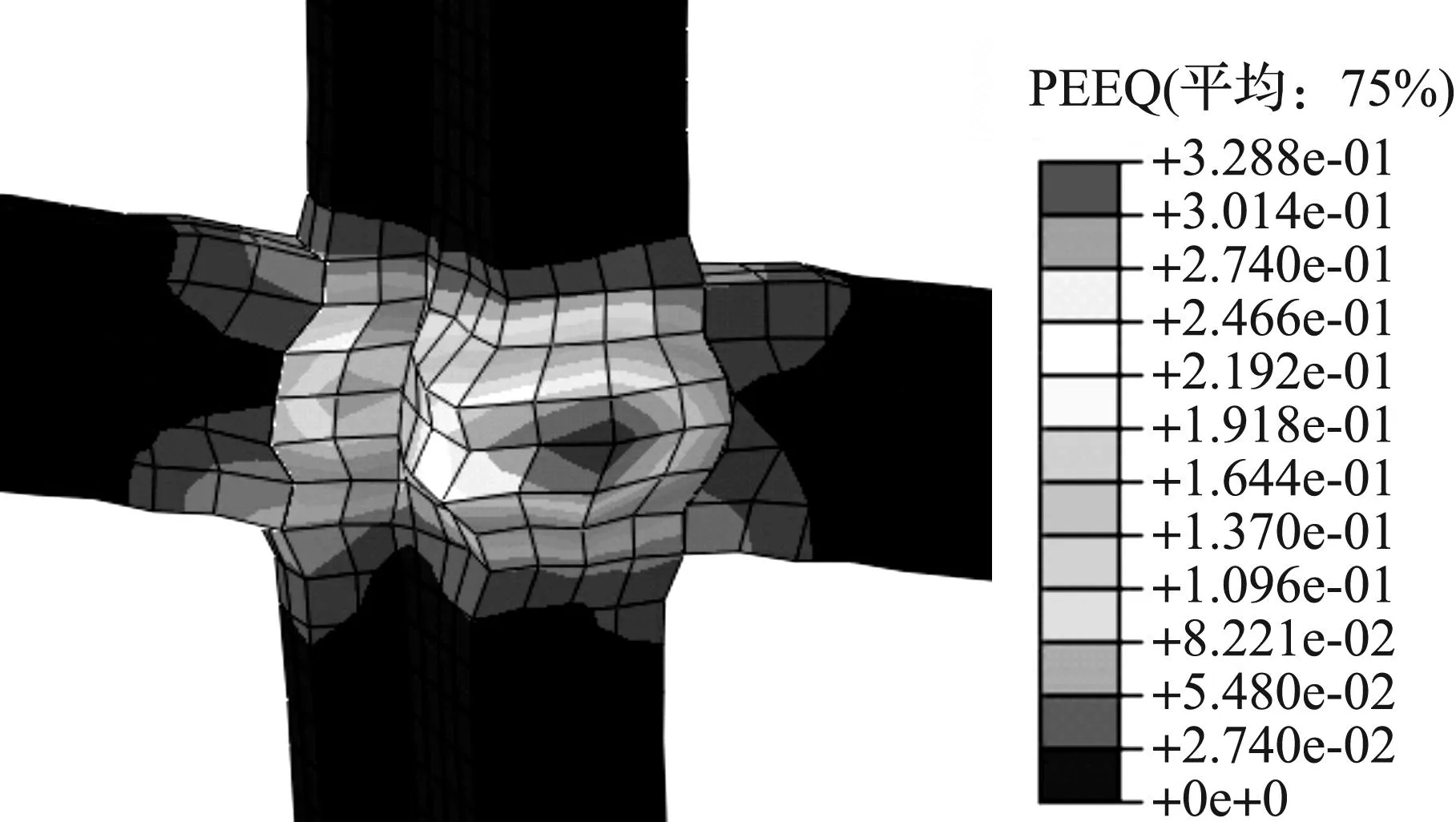
图6　JD2等效塑性应变(PEEQ)云图Fig.6　Equivalent plastic strain cloud of JD2

图7　JD2现场照片Fig.7　Test picture of JD2

4结论

通过能量等价原理与GB 50010—2010《混凝土结构设计规范》附录C[8]中的混凝土本构模型结合得到的损伤因子可以较好的模拟Z形柱框架节点混凝土的塑性损伤，ABAQUS仿真结果与试验结果吻合较好，由于钢筋和混凝土在受荷过程中会产生一定的滑移会影响计算结果，建议黏性系数取值在0.000 1～0.000 5之间，可为实际工程中Z形柱设计提供参考.只选用了两种混凝土本构模型，并未验证其他本构模型对Z形截面柱框架节点仿真情况，有待进一步研究.

参考文献：

[1]崔钦淑,杨俊杰,康谷贻.钢筋混凝土Z形截面柱框架节点抗震性能试验研究[J].建筑结构学报,2012,33(6):86-95.

[2]朱振华,杨俊杰,陈瑞生，等.不同轴压比条件下Z形截面混凝土柱梁柱节点抗剪性能试验研究[J].浙江工业大学学报,2011,39(1):57-60.

[3]杨俊杰,徐良德,崔钦淑，等.翼缘长与梁高的比值对Z形柱梁柱节点抗震性能的影响[J].浙江工业大学学报,2013,41(1):76-79.

[4]傅剑平,张笛川,韦峰，等.异形柱框架中间层端节点抗震性能试验研究[J].建筑结构,2005,35(9):66-72.

[5]马乐为，陈昌宏，张同亿.T形柱框架节点受剪承载力的非线性有限元分析[J].西安建筑科技大学学报(自然科学版),2006,38(2)：232-235.

[6]季青，杨俊杰，陈瑞生，等.低周反复水平荷载下不同轴压比Z形截面混凝土柱受力性能数值分析[J].浙江工业大学学报,2011,39(3)：282-286.

[7]SIDOROFF F. Description of anisotropic damage application to elasticity [C]//Proceedings of the IUTAM Colloqium on physical Non-Linearities in Structural Analysis.Berlin：Springer-Verlag，1981：237-244.

[8]中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010—2010[S].北京：中国建筑工业出版社，2010.

[9]冉俣，邢国华，牛荻涛，等.FRP(钢绞线)加筋混凝土梁正截面受弯承载力计算[J].防灾减灾工程学报,2014,34(1)：85-90.

[10]SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoopsat low and high strain rates[J].ACI journal,1982,79(1):13-27.

[11]聂建国，王宇航.ABAQUS中混凝土本构模型用于模拟结构静力行为的比较研究[J].工程力学,2013,30(4)：59-82.

(责任编辑：刘岩)

ABAQUS-based modeling analysis for the frame joints of RC Z-shaped columns

CUI Qinshu, NI Zhenqiang

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:The damage plastic model of concrete is a material one provided in the finite element software ABAQUS. It can better describe the material characteristic of concrete. An expression of the damage factor is derived based on the damage model parameters of concrete provided by the software ABAQUS and the energy equivalence principle proposed by Sidiroff. This damage plastic model is of higher modeling accuracy and can be used for the design and analysis of complicated concrete structures. The modeling analysis of the frame joints of Z-shaped columns is conducted with the software ABAQUS. Two constitutive relationships of concrete, provided in the code and presented by Hongnestad, respectively, are adopted and the equivalent plastic strain cloud in concrete is obtained. The calculated load-displacement curve at the joint is compared with test results. The optimal range of the viscous coefficient is given, which provides reference for engineering applications.

Keywords:Z-shaped RC column; frame joint; damage factor; nonlinear finite element analysis; ABAQUS

收稿日期：2015-06-30

基金项目：浙江省自然科学基金资助项目(LY14E080007)

作者简介：崔钦淑(1963—)，女，山东莱西人，副教授，研究方向为混凝土异形柱结构抗震性能,E-mail：cuiqinshu@163.com.

中图分类号：TU375.3

文献标志码：A

文章编号：1006-4303(2016)02-0212-04