基于Hough变换圆检测的方法研究
2016-06-17李博学李鹤沈阳工学院
李博学 李鹤沈阳工学院
基于Hough变换圆检测的方法研究
李博学 李鹤
沈阳工学院
摘要:本文研究一种基于MATLAB仿真平台的圆检测算法。在对图像进行降噪滤波、边缘检测等预处理后,利用Hough变换检测前景图像中的圆心位置,然后以圆心为起点,设定的半径步长与角度步长为度量单位,检测圆形的具体位置。
1 引言
关于圆形的检测方法目前已有很多文献进行了相关论述。最常见的算法还是利用Hough变换来实现检测,主要是因为Hough变换具有对圆度误差灵活的处理能力,以及对类圆强大的近似识别能力。Hough变换利用点与线的对偶性,将图像空间给定的曲线表达形式变成参数空间的一个点。这样就把原始图像中给定曲线的检测问题转换为寻找参数坐标中的峰值问题。本文需要研究的内容就是如何在matlab平台上实现这一圆检测算法。
2 Hough变换理论
2.1 Hough变换的数学解释
需引入直线表达式:y=kx+b,其中k和b是参数,分别是斜率和截距。过某一点(x0,y0)的所有直线的参数都会满足方程y0=kx0+b。即点(x0,y0)确定了一组直线。方程y0=kx0+b在参数k--b平面上是一条直线。这样,图像x--y平面上的一个前景像素点就对应到了参数平面上的一条直线。
以上解释可举例分析:已知y=x,取点A(0,0)、B(1,1)、C(2,2)。易解于A点,b=0。B点,1=k+b。C点,2=2k+b。三函数在参数坐标空间(k,b)交点(1,0),即峰值为(1,0)。
2.2 软件实现可行性分析
(1)需初始化一块缓冲区作为参数空间,对应参面的所有点数据为0。(2)对于前景像素点在参面所对应的直线所有点+1。(3)利用统计特性找到峰值,确定前景图像中的直线,峰值并不唯一,对应的是前景图像的个数。
由于Y=kx+b无法表示y=c(k=inf)所以,采用参数方程,既可以表示简单,又可以简化计算。P=xcos(theta)+ysin (theta),参数空间变量为(p,theta)。
基于以上分析解释得到Hough变换的具体函数表达式:
Xcos(θ)+ycos(θ)=ρ
3 Hough变换圆检测算法实现
3.1 算法概述
该算法通过a = x-r*cos(angle),b = y-r*sin(angle)将圆图像中的边缘点映射到参数空间(a,b,r)中,由于是数字图像且采取极坐标,angle和r都取一定的范围和步长,这样通过两重循环(angle循环和r循环)即可将原图像空间的点映射到参数空间中,再在参数空间(即一个由许多小立方体组成的大立方体)中寻找圆心,然后求出半径坐标。
3.2 算法实现步骤:
Step1.图像灰度化,利用sobel算子实现二值化。
Step2.检测边缘点,保存位置。设置角度theta、半径r变换范围步长。
Step3.X=a+rcos(theta) Y=b+rsin(theta)求a,b。
说明:(x、y)图像空间边缘点坐标,(a、b)为参数空间的变量,a、b为可加量。
4 实验仿真
4.1 实验步骤
Step 1:首先使用中值滤波器降噪,再自动阈值分割粒子,canny算子提取边缘,并骨架化至二值图像,平滑滤波。
Step 2:输入参数。最大圆半径r_max;最小圆半径r_min;半径步长step_r;角度步长step_angle;以参数空间p*hough_ space的最大值为阈值p(0,1之间)
Step 3:插入算法实现。
Step 4:显示变换后图形。
4.2检测结果
待检测图片如图1所示,包括3个白球和1个黑球,检测后的结果如图4所示,能够检测出4个球的位置,多次检测证明,检测误差在3%之内。

图1 待检测图像
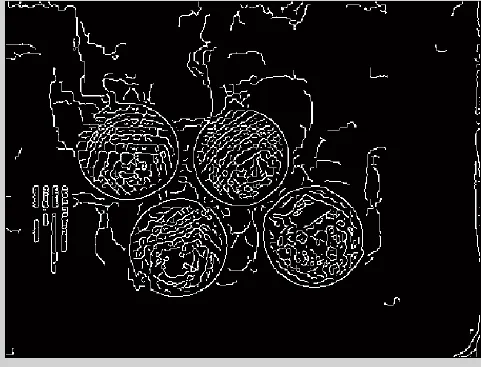
图2 检测结果
参考文献
[1]杨丹,赵海滨,龙哲等.MATLAB图像处理实例详解[M].北京:清华大学出版社,2013.
[2]薛山.MATLAB基础教程[M].北京:清华大学出版社,2011.
[3]王耀南.计算机图像处理与识别技术[M].北京:高等教育出版社,2001:11-281.
作者简介
李博学(1997—),男,辽宁沈阳人,在读本科生,研究方向:图像处理与识别。
李鹤(通讯作者),男,辽宁省沈阳人,讲师,就职于沈阳工学院信息与控制学院。研究方向:人工智能算法。
