一种基于改进人工蜂群的K-means聚类算法

刘川川，丁海军（河海大学物联网工程学院，常州　213022）



一种基于改进人工蜂群的K-means聚类算法

刘川川，丁海军
（河海大学物联网工程学院，常州213022）

摘 要：针对K-means算法对初始的聚类中心选择敏感，全局搜索能力较差，聚类精度低以及稳定性不高，算法的鲁棒性较差等缺点，提出了一种基于改进的人工蜂群算法来对K-means聚类算法进行优化。算法构造了新的适应度函数，改进了食物源的位置更新公式来提高迭代效率。利用改进的人工蜂群算法良好的全局寻优能力，搜索速度快等优点，再加上K-means收敛速度快的优点，二者结合来提高算法的鲁棒性。将改进后的算法嵌入到WEKA这一数据挖掘平台中，充分利用了开源WEKA中的类和可视化功能，与WEKA中已有的聚类算法对比分析，可以获得更好的聚类结果。

关键词：聚类；人工蜂群算法；K-means算法；适应度函数；位置更新公式；WEKA平台

1 引 言

聚类分析是一种无监督的学习，它不需要数据集的先验知识，在图像识别、机器学习等领域有广泛的应用，是数据挖掘领域中的一个重要研究方向。聚类算法就是将数据对象划分为不同的多个簇，同一个簇中的对象尽可能相似，不同簇中的对象尽可能相异。K-means算法是目前使用广泛的一种基于划分的聚类算法［1］，该算法对初始聚类中心点的选择较为敏感，选择不同的初始聚类中心点，对聚类结果有比较大的影响。目前，已经有很多学者针对初始聚类中心的选择进行了研究，文献［2］中作者提出一种通过计算每个数据对象的密度，从中选取k个高密度分布的点作为初始聚类中心，有效提高了K-means聚类算法的准确率和稳定性。文献［3］运用最大最小距离法选择初始聚类中心，将原始数据集分割成各个小类，然后用合并算法形成最终类，聚类性能也优于K-means算法。文献［4］作者在基于密度概念的基础上，采用最大距离积法选取初始聚类中心，使得改进的K-means算法有更高的准确率和准度，并且稳定性也有一定提高。文献［5］提出的算法中K的个数不需要预先给定就可以完成聚类。

人工蜂群智能算法（ABC）是Karabog受到蜜蜂启发提出的一种基于蜜蜂群体采蜜行为的群体智能算法。人工蜂群算法具有搜索速度快、全局寻优能力强、适用领域广泛等优点。但是人工蜂群算法存在迭代后期收敛速度较慢，容易陷入局部最优等问题。文献［6］通过引入了人工蜂群的粒子算法，利用人工蜂群的全局搜索能力和粒子群的局部搜索能力，使得优化后的算法收敛速度较快，跳出局部最优能力也比较强。文献［7］通过引入反向学习的初始化，提高了求解效率和质量。

基于K-means和ABC算法的各自优缺点，首先对传统的人工蜂群算法进行了改进，提出了改进的人工蜂群算法（Improved ABC，IABC），修改了食物源的搜索公式，并在迭代过程中使用新的适应度函数公式来加快算法的收敛速度，并将改进后的人工蜂群算法与K-means聚类算法相结合，具有良好的聚类效果。

2 相关算法介绍

2.1K-means算法

K-means算法的基本思想：首先随机的从N个数据对象中抽取K个对象作为初始聚类中心；针对剩下的其它对象，根据它们与这些中心点的相似度，将其划到相似度最大的聚类中；然后再更新每个聚类的聚类中心，再进行聚类划分，重复这一过程直到偏差准则函数开始收敛。偏差准则函数一般定义如下：

其中：K为聚类簇的总个数，Xi为簇Ci的平均值。

K-means算法的步骤描述如下：

（1）随机选择K个数据对象作为初始簇中心；

（2）计算每一个数据对象与K个簇中心点的距离，将其划分到距离最近的那个簇中；

（3）重新计算K个簇的中心，中心为该簇内所有数据对象点的平均值；用公式（1）计算出此时的偏差准则函数E。

（4）如果偏差准则函数满足：

|E2-E1|＜ε（2）

其中：ε是一个极小值，E2和E1分别代表了两次迭代后的准则函数值。当满足公式（2）时，则表示偏差准则函数收敛，各个簇内的数据对象不会再发生改变，结束聚类。

2.2人工蜂群算法

人工蜂群算法（ABC）主要由食物源、引领蜂、跟随蜂和侦察蜂来组成。引领蜂用来维持优良解，跟随蜂加快算法的收敛速度，侦察蜂增强了摆脱局部最优的能力。一般情况下，引领蜂和跟随蜂各占蜂群总规模的一半，且每个食物源同时段内只允许有一只引领蜂采蜜。每个食物源的位置代表所求优化问题的一个可能解，适应度的大小代表了解的质量。

ABC算法中，首先根据公式（3）随机的产生N个初始的解｛X1，X2，X3…XN｝，每一个Xi（i =1，2，3 …N）都是D维的，并且计算其适应度，根据适应度的高低排序，将前一半的蜜蜂作为引领蜂，后一半作为跟随蜂。

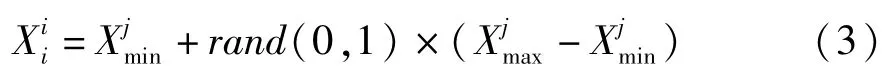
其中：j =（1，2，3，…，D），rand（0，1）为［0，1］之间的随机数。

搜索开始阶段，引领蜂在当前位置附近进行领域搜索，根据公式（4）产生一个新的位置：

Vij= Xij+φij（Xij-Xkj）（4）

其中k∈｛1，2，3…N｝，且j∈｛1，2，...D｝，φij是［-1，1］均匀分布的随机数，Xij为当前食物源的位置，Vij为引领蜂搜索后随机产生的领域食物源位置。

引领蜂采蜜采取贪婪选择的方法，将记忆中的最优解和搜索到的解相比较，如果搜索到的解适应度大于记忆中的最优解时，替换搜索解为最优解；否则，保留最优解不变。

当所有的引领蜂完成了公式（4）后，飞回交流区和跟随蜂来共享食物源位置信息，跟随蜂根据轮盘赌原则来进行引领蜂的选择。然后跟随蜂再根据公式（4）在引领蜂附近进行领域搜索，同样根据贪婪原则保留最优解。

在ABC算法中，跟随蜂根据公式（5）的概率来选择引领蜂

其中：fiti为第i个解的适应度，适应度越大，对应解的质量越高。

如果在经过limit次迭代后某个食物源位置没有发生变化，并且该食物源也不是全局最优解，则放弃该食物源，同时与之对应的引领蜂脚色发生变化，将转变为侦察蜂，由侦察蜂根据公式（3）随机产生新的位置代替该解。当达到最大迭代次数后，将适应度最大的解作为最终结果输出。

3 改进的人工蜂群算法研究

3.1适应度函数

其中E为K-means算法中的偏差准则函数，也可称为所有簇的类内距离和。

3.2食物源位置更新公式

在传统的人工蜂群算法中，引领蜂和跟随蜂都是根据公式（4）来更新位置的，由于引领蜂和跟随蜂都是在一个范围内随机搜索附近的食物源，没有具体的方向和范围，势必会具有盲目性。而在实际寻优的过程中，搜索范围在不同的时期要求是不一样的。在算法刚开始的阶段，希望引领蜂能够在较大的范围内进行搜索，从而能够快速找到最优解的大概方向；而随着迭代次数的增加，即到了算法后期，此时由于已经比较接近最优解，希望能够在较小的范围内搜索最优解。即越到算法的后期，搜索范围相比初始阶段，也应该相应的越来越小，所以改进后的领域搜索公式为：

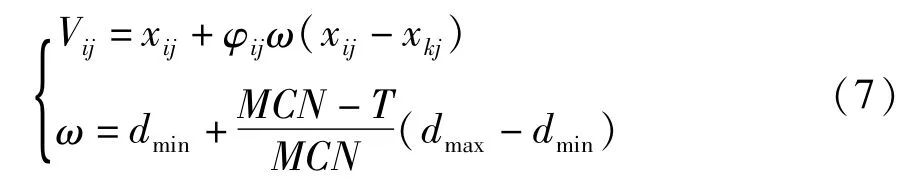
其中：MCN为最大迭代次数，T为当前迭代次数。dmin和dmax用来控制领域搜索的最小、最大范围，根据经验值，取dmin=0.4，dmax=1.0。

4 基于改进人工蜂群的K-means算法

基于改进人工蜂群的K-means算法的实现过程：首先随机产生初始蜂群，每个蜜蜂代表一种聚类划分，利用人工蜂群算法得到多个聚类中心，再将每个聚类中心进行K-means迭代，从而得到新的聚类中心，两个算法相互迭代，交替进行，直到聚类结束。

算法的具体步骤描述如下：

a.设置引领蜂、跟随蜂以及侦察蜂的数量（引领蜂数量=跟随蜂数量=蜂群规模的一半），设置最大迭代次数MCN，当前迭代次数T，T的初始值为1，聚类数K，设置预先的试验次数上限limit，并随机产生｛Z1，Z2，Z3…ZN｝个初始蜜蜂。

b.对蜂群进行一次聚类划分，每个蜜蜂代表一种聚类划分，并按照公式（6）计算每个蜜蜂对应的适应度fi。

c.将适应度从高到低排序，将前50%的作为引领蜂，剩下的50%作为跟随蜂。

d.引领蜂根据公式（7）进行领域搜索，按照贪婪选择的方法更新得到新位置，如果新位置的适应度值大于旧位置的适应度，则用新位置代替旧位置；反之，保持不变。

e.跟随蜂依据轮盘赌原则来选择引领蜂，选择跟随完成后也按照公式（7）进行领域探索，同样根据贪婪选择的方法来更新位置，将新位置作为新的聚类中心。

f.当全部跟随蜂完成了领域搜索后，得到多个新的聚类中心，将聚类中心作为K-means的初始聚类中心，进行一次K-means聚类算法，更新得到新的聚类中心，用新的聚类中心再去更新蜂群。

g.如果某个引领蜂在经过limit次迭代后位置没有发生改变，则该位置会被放弃，此时，引领蜂变为侦察蜂，由侦察蜂按照公式（3）随机产生新的位置取代原位置。

h.如果当前迭代次数等于最大迭代次数，输出适应度最大的聚类结果，算法结束。否则，转向步骤b），T = T +1。

5 算法实现与性能测试

5.1基于改进人工蜂群的K-means算法实现

根据以上的算法思想过程描述，在WEKA平台上利用Java语言（Eclipse环境）实现了改进人工蜂群的K-means算法，并且将该算法嵌入到了WEKA平台中。充分利用WEKA源代码开源的这一特性，所开发的改进人工蜂群的K-means算法的主类IABCK-means充分调用了原有类如weka.core、weka.classifiers.rules、java.util等包中的一些类，最后将开发的主类IABCK-means与Cluster及RandomizableClusterer抽象类等一起封装在weka.clusterers包中。IABCK-means类实现了NumberOf-ClustersRequestable、WeightedInstancesHandler这两个接口，并且IABCK-means类继承了RandomizableClusterer抽象类。在ABCK-means类中主要完成了聚类模型的产生和聚类结果的表示等。

5.2基于改进人工蜂群的K-means算法性能测试

5.2.1 实验数据及结果分析

为了验证改进人工蜂群的K-means算法性能，将该算法嵌入到WEKA平台后，采用了UCI［9］数据库中著名的鸢尾花（Iris）数据集（表1）。在该数据集中，一共包含150个鸢尾花的数据信息，每组数据包含四种属性：花瓣长度、花瓣宽度、萼片长度和萼片宽度。数据集包含三类：Setosa、Versicolour 和Virginica。Iris数据集中3个类分类特征相对明显，第一类与第二类、第三类完全分开，后两个类有一定的交叉。

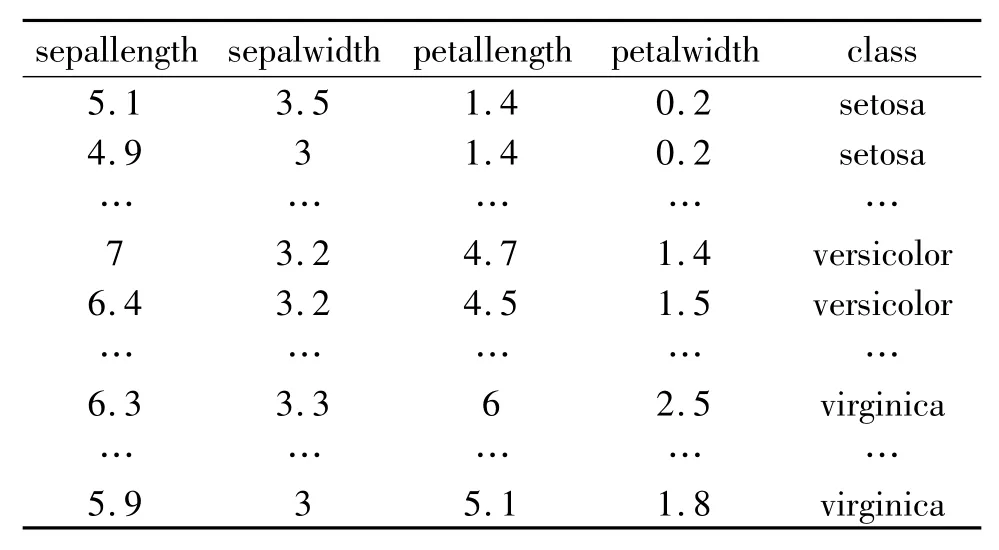
表1 鸢尾花的实验数据

算法的参数设置为：最大迭代次数MCN =200，蜂群规模为N =20（即引领蜂=跟随蜂=10），控制参数limit =50，聚类数目K =3。

文献［8］中作者给出了鸢尾花数据集的实际类中心位置：Z1=（6.58，2.97，5.55，2.02），Z2=（5.00，3.42，1.46，0.24），Z3=（5.93，2.77，4.26，1.32）。从表2中看出，采用改进的人工蜂群的K-means聚类算法所得的结果与实际结果非常接近，聚类中心与实际的聚类中心几乎一致。说明经过改进的人工蜂群算法后的聚类中心比较接近最终的聚类中心，能够克服K-means聚类算法容易受到初始聚类中心影响这一缺点，能够提高算法的稳定性。

表2 最终的聚类中心

除了Iris数据集外，还对Zoo数据集进行了实验。Zoo数据集包含15个数值属性和1个分类型属性。数据集样本一共由7个动物类别组成，分别是：哺乳类（41）、鸟类（20）、昆虫类（8）、鱼类（13）、爬行类（5）和两栖类（4）。在Zoo数据集中，算法的参数设置为：最大迭代次数MCN =500，蜂群规模= 20，控制参数limit =100，聚类数目K =7。实验分析计算了在不同数据集的情况下，WEKA中经典聚类算法的准确率，结果如表3所示。

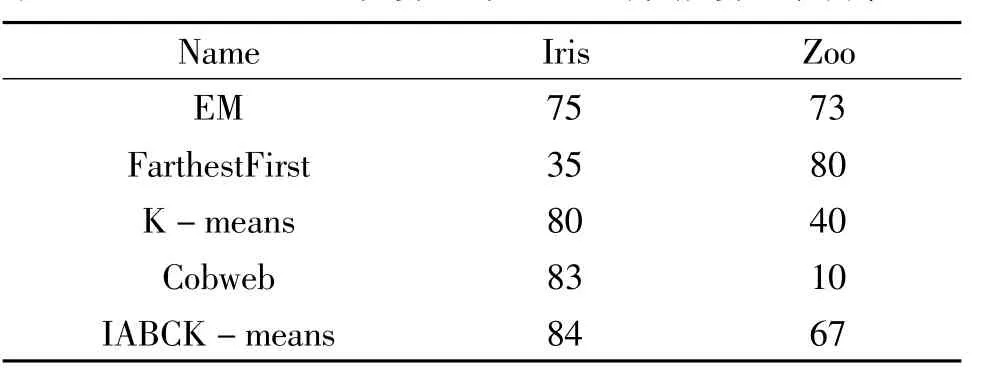
表3 IABCK-means聚类算法与WEKA中其他算法准确率对比

准确率的计算方法如下：原数据集分为K个类，Ci表示第i类，Ni为第i个类中的样本个数，Mi为聚类完成后第i个类中的样本个数，设准确率为P，则：

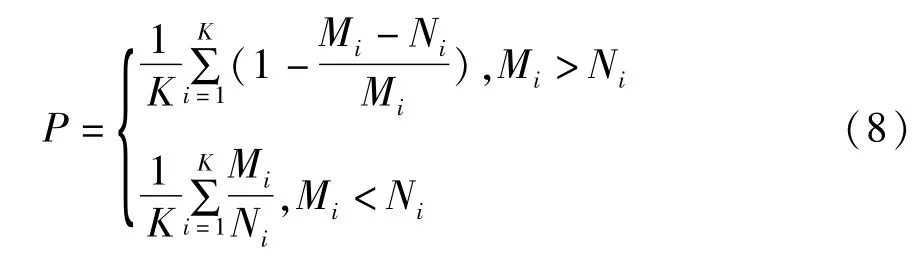
6 结束语

在人工蜂群算法基础上，提出了一种改进的人工蜂群算法，采用新的适应度函数公式，改进了食物源的位置更新公式，增强了局部寻优能力。将改进后的算法与K-means聚类算法相结合，利用人工蜂群算法全局寻优能力强、算法鲁棒性较强等优点去对K-means初始聚类中心点进行优化，提高了算法的鲁棒性。在数据集Iris和Zoo的实验中，与传统的K-means算法相比，该算法在稳定性和收敛精度等方面都有了一定提高，证明该算法具有较好的聚类效果。但是也存在一定的缺点，如算法耗时较长，需要预先指定要聚类的数目，这些都可以作为下一步改进的研究方向。

参考文献：

［1］Han Jiawei，Kamber M.数据挖掘：概念与技术［M］.范明，译.北京：机械工业出版社，2007：223-244.HAN J，Kamber M.Data mining：Concepts and Techniques［M］.FAN M，translation.BeiJing：China Machine Press，2007：223-244.

［2］韩凌波，王强，蒋正锋，等.一种改进的k-means初始聚类中心选取算法［J］.计算机工程与应用，2010，46 （17）：150-152.HAN L，WANG Q，JIANG Z，et al.A modified K-means the initial clustering center selection algorithm［J］.Computer Engineering and Applications，2010，46（17）：150-152.

［3］周涓熊，熊忠阳，张玉芳，等.基于最大最小距离法的多中心聚类算法［J］.计算机应用，2006，26（6）：1425-1427.ZHOU J，XIONG Z，ZHANG Y，et al.Multiseed clustering algorithm based on max-min distance means［J］.Journal of Computer Applications，2006，26（6）：1425-1427.

［4］熊忠阳，陈若田，张玉芳，等.一种有效的K-means聚类中心初始化方法［J］.计算机应用研究，2011，28 （11）：4188-4190.XIONG Z，CHEN R，ZHANG Y.Effective method for cluster centers'initialization in K-means clustering［J］.Application Research of Computers，2011，28（11）：4188-4190.

［5］刘雷，王洪国.一种基于蜂群原理的划分聚类算法［J］.计算机应用，2011，28（5）：1699-1702.LIU L，WANG H.A partitioning clustering algorithm based on swarm principles［J］.Journal of Computer Applications，2011，28（5）：1699-1702.

［6］高卫峰，刘三阳，焦合华，等.引入人工蜂群搜索算子的粒子群算法［J］.控制与决策，2012，27（6）：833-838.GAO W，LIU S，JIAO H，et al.The introduction of artificial colony search operator particle swarm algorithm［J］.Control and Decision，2012，27（6）：833-838.

［7］吴昱，李元春，徐星.基于群智能的新型反向混合差分进化算法［J］.小型微型计算机系统，2009，30（5）：903-907.WU Y，LI Y，XU X.Oppositional hybrid differential evolution algorithm based on swarm intelligence［J］.Journal of Chinese Computer Systems，2009，30（5）：903-907.

［8］CHEN Ning，CHEN An，ZHOU Long-xiang.Fuzzy K-prototypes algorithm for clustering mixed numeric and categorical valued data（in English）［J］.Journal of Software，2001，12（5）：712-716.

［9］University of California，Irvine，UCI machine learning repository［DB/OL］.［2013-06-19］.http：//archivce.ics.uci.edu/ml.

A K-means Clustering Algorithm Based on Improved Artificial Bee Colony

Liu Chuanchuan，Ding Haijun
（College of Internet of Things Engineering，Hohai University，Changzhou 213022，China）

Abstract：As the K-means clustering method has disadvantages of sensitive to the initial clustering centers，poor global search ability，low accuracy and stability and poor robustness of algorithm，based on an improved Artificial Bee Colony algorithm，this paper proposes an algorithm to optimize the K-means clustering algorithm.It will construct a new fitness function and improve the food source location update formula to enhance the efficiency of iteration.The advantages of good global optimization ability，fast search and convergence rate are combined to improve the robustness of the algorithm.The improved algorithm is embedded in the WEKA platform，compared with the existing clustering algorithms in the WEKA，the better clustering results can be obtained.

Key words：Clustering；Artificial Bee Colony；K-means algorithm；Fitness function；Position update rule；WEKA platform

DOI：10.3969/j.issn.1002-2279.2016.02.013

中图分类号：TP301.6

文献标识码：A

文章编号：1002-2279（2016）02-0047-04

作者简介：刘川川（1989-），男，河南省洛阳市人，硕士研究生，主研方向：数据挖掘，智能数据处理。

收稿日期：2015-05-25