我国外汇储备的结构优化研究
2016-06-16刘永辉尚星佩
刘永辉++尚星佩

摘要:随着外汇储备规模的不断扩大,储备资产的结构以及风险管理日渐重要。选取2009年1月至2014年12月期间美元、欧元、日元、英镑、澳元、加元以及石油和黄金等八个代表性的储备资产的日收益率数据,通过使用两次绝对偏差模型(MAD模型)计算资产的最优配置,使用VaR-GARCH模型进行配置资产的风险管理,可进一步优化我国外汇储备资产的结构,满足外汇储备管理的安全性原则。
关键词:外汇储备;MAD模型;GARCH模型;储备货币;外汇组合风险;外汇储备结构
中图分类号:F832.6 文献标识码:A 文章编号:1007-2101(2016)04-0045-07
一、引言
改革开放三十多年来,中国经济高速发展,其中,对外贸易居功至伟。特别是中国加入WTO以来,由于国际投资者看好中国经济形势,大量资本进入国内。贸易、资本双顺差使得我国外汇储备长期累积并占据了世界第一的位置。截止到2014年末,我国外汇余额已有3.84万亿美元。巨额的外汇储备为我国开放经济的平稳发展起到了重要作用,同时管理巨额外汇储备的投资风险也面临巨大挑战。
国际货币基金组织(IMF)2014年第四季度公告了发展中国家的外汇储备结构:美元为62.25%,欧元21.48%,日元3.16%,英镑4.48%,加拿大元2.23%,澳元2.07%,其他货币总共占比3.93%。由于我国外汇储备规模在发展中国家占比极大,由以上数据推测我国约有60%的外汇储备投资于美元资产,欧元也占到20%左右。最近研究显示,在国际金融大环境处于长期动荡的背景下,如何平衡风险与收益之间的关系,合理确定外汇的储备结构,已然成为学界研究的热点。
关于外汇储备结构,国外学者很早就开展过相关的研究。比较著名的理论有:Markowitz的资产组合选择模型、Heller和Knight模型以及Dooley模型。通过对外汇储备币种构建Markowitz(1952)的资产组合选择模型,可对各种储备货币的风险和收益进行优化分析。Heller和Knight(1978)通过建立计量模型,关注一国的贸易收支结构和汇率制度,来对该国的外汇管理进行研究。Dooley(1989)等对Heller-Knight模型进行了补充,指出外汇资产结构是贸易流量、外币支付流量和汇率制度共同影响的结果。
外汇储备结构研究的另一个方向是运用VaR方法,综合运用其他模型,从降低外汇风险的角度来优化外汇币种结构。Zong-RunWang等(2010)运用GARCH—EVT—Copula模型,并结合VaR(CVaR)方法,对外汇组合风险进行研究。同时运用多元Copula将研究结果进行扩展,解决了从二维扩展到n维的资产配置问题。姜昱、邢曙光(2010)通过DCC-GARCH-CVaR模型研究了我国外汇储备的汇率风险,并在此基础上,运用Mean-CVaR模型确立我国外汇储备的最优结构。阎素仙、张建强(2012)选取美元、欧元、日元、英镑作为我国外汇储备资产,并运用VaR-GARCH方法及边际VaR工具进行分析,最终给出了降低欧元比重,适当提高日元、英镑比重的结论。余湄、何泓谷(2013)选取8种具有代表性的外汇储备资产,运用绝对偏差模型来计算我国外汇储备的最优结构,结果表明我国需提高澳元、日元占比,降低美元比例。周光友、赵思洁(2014)为研究中国外汇储备的结构风险,利用GARCH模型,结合VaR算法,实证分析了在不同预期收益率假设下的我国外汇储备的最优结构。王桐(2015)以杜利模型为基础,综合考虑我国进出口贸易、外商投资、我国外债以及各储备国的经济实力等要素,并添加未来中国国际政治经济战略(一带一路、亚投行、中韩自贸协定等)作为考量因素,得出我国外汇资产币种结构为:美元55.87%,日元10.37%,欧元18.23%,韩元6.90%,其他货币8.62%。陈珂、徐丹萍和杨胜刚(2015)借鉴了Makin(1971)的方法构建外汇储备币种结构,讨论在效用最大化的情况下,储备资产的安全性、流动性和盈利性三者之间的权衡,通过运用协整分析、格兰杰检验得出我国外汇储备投资总体是风险规避型的。
纵观国内外研究可以看出,尽管学者们从不同角度对外汇储备的币种结构做了深入研究,但是仍然存在一些不足:首先,从“鸡蛋不要放在一个篮子里”的角度来看,大多数研究选择储备资产的种类仍然偏少,导致外汇组合风险没有很好的分散;其次,采用均值方差模型研究外汇储备的结构,需要假设收益率分布的正态性,然而实际情况是外汇资产的收益率分布一般不服从正态分布;最后,使用绝对偏差模型虽然避免了正态性假设的难题,但明显没有考虑风险的因素。
针对以上研究中存在的不足,本文从外汇资产的选择以及优化方法的选用两个方面都做了创新。首先,在外汇储备资产的选择上,选取了美元、欧元、日元、英镑、澳元、加元以及石油和黄金八种资产;其次,在优化方法的选取上,两次运用了绝对偏差模型,特别是在第二次使用绝对偏差模型时不仅考虑了贸易方向和外债结构等刚性约束,更考虑了利用GARCH模型计算出来的外汇储备风险值的约束,解决了上述文献研究中存在的一些不足,实现了收益和风险的新均衡。
二、基于GARCH模型的动态VaR测度
(一)GARCH模型
GARCH模型的数学表达式如下:
xt=β0+β1xt-1+β2xt-2…+βpxt-s+ut
ut=σtεt
σt2=α0+∑pi=1αiσ2t-i+∑qj=1θju2t-j
其中α0>0,αi≥0,θj≥0。
GARCH的基本思想是在ARCH模型的基础之上,用一个或两个以上ut平方滞后值代替许多σ2t的滞后值。GARCH(p,q)中的(p,q)是指方差设定中含有q个GARCH项与p个ARCH项。
(二)动态VaR测度
VaR是在正常的市场条件下和给定的置信度内,某一金融资产或资产组合在未来特定持有期内的最大可能损失。用统计学公式表示为:
P(ω(Δt,x)≤VaR)=1-C
其中x为风险因素(如利率、汇率等市场因子),C为置信水平,Δt为持有期。
ω(Δt,x)=ω(t,x)-ω(t0,x)
(大于0时为收益,小于0时是损失)为损益函数,ω(t0,x)为资产的初始价值,ω(t,x)为时刻t资产的预测价值。
从VaR的统计定义可以看出VaR值是由持有期Δt、置信水平C、风险因子x这三个基本要素组成的。
估计条件方差的方法属于动态VaR计算的分析方法,可以利用下式计算每日的VaR值:
VaR(i)=Δ+Zc*σ(i)
其中Zc是相应标准化条件分布的上侧分位数,C为置信水平,Δ根据GARCH类模型的均值方程确定,σ(i)是根据GARCH类模型计算出来的条件方差。
(三)VaR模型的事后检验
我们使用Kupiec提出的LR检验法来进行VaR模型的准确性检验。该方法是对VaR模型估计风险过于激进或保守的权衡,能够全面检验模型的准确性。假定失败的期望概率为:■=1-C(C为置信度)。零假设为■=p。Kupiec提出了对零假设最合适的检验是似然比检验:
LR=-2ln[(1-■)n-N■N]+2ln[(1-p)n-NpN]
在零假设条件下,统计量LR~χ2(1)。自由度为1的卡方分布的99%置信区间的临界值为6.635。所以当计算出的LR值大于临界值时,拒绝模型。
三、我国外汇储备的结构优化实证分析
(一)我国外汇储备资产选择与数据的收集
2012年11月19日,澳元和加元两个币种被国际货币基金组织认可为官方储备货币。同时2013年以后,两个币种在各个成员国的持有量也被独立公告出来,这表明澳元和加元在国际结算中将被越来越广泛使用。另外,黄金储备已然成为衡量当今世界各国财富硬实力的指标,拥有更多的黄金储备意味着在世界贸易体系中,国家应对金融风险的能力更加强大。石油作为我国工业经济命脉资源之一,其与充足的煤炭资源相比,储存量不足。除了进一步开发国内的石油资源外,利用外汇储备的方式解决石油长期缺乏的难题已迫在眉睫。基于上述原因,考虑到我国对外贸易结构和外债币种结构,本文选取美元、欧元、日元、英镑、澳大利亚元、加拿大元、黄金和石油作为我国外汇的储备资产。
根据实证的需要,本文选取美元、欧元、日元、英镑、澳大利亚元和加拿大元间接标价法下的每日汇率,黄金和石油的日价格,以及美国、欧盟、日本、英国、澳大利亚和加拿大5年期国债的日收益率。数据来自于Wind数据库,截选了2009年1月至2014年12月的日数据。
(二)不同资产收益率的计算
一种货币的收益率受到汇率和该种货币利率的影响。货币收益率计算需要考虑两个方面:货币的利息收益以及货币之间兑换的潜在收益率。令Ei0表示期初时人民币对第i种货币的汇率,Eit表示期末时人民币对第i种货币的汇率。则:
Ii=ri■,Ei=■-1
货币的收益率为:Ri=Ii+Ei。
黄金和石油的日收益率为:Rt=■。
(三)资产收益率描述性统计分析
从表1可以看出,均值最大的为澳元,其次为加元和英镑,由此可知澳元、加元和英镑近几年来收益率较高,表现良好。从方差、标准差角度分析八种资产的风险性,可以看出美元的标准差最小,其次是日元、加元、英镑、欧元、黄金、澳元,标准差最大的是石油。
分析八种资产收益率是否符合正态分布。从描述性统计数字出发,可看出偏度系数显著不等于0,峰度系数也不满足正态条件。通过使用Shapiro-Wilk统计检验方法,对八种资产的收益率分布进行正态性检验,我们得到八种资产的W检验统计量都大于0.95,故八种资产收益均不符合正态分布。
(四)MAD模型下我国外汇储备结构
传统的均值方差模型需要假设货币的收益率满足正态分布的条件,而前文分析中的条件并不满足。故本文利用Yamakaz和Komno(1991)提出的绝对偏差模型来计算外汇储备最优配置比例。
带有贸易方向和外债结构约束条件的MAD模型:
其中Ri为资产i的收益率,ri=E(Ri),xi为投资者投资在资产i的比例,假设不允许卖空,即xi>0。其中TDi用我国从某国进口额除以我国进口总额得出,DEi表示我国外债中持有的某币种的头寸。在计算权重时,用我国2009—2014年的进口贸易比例及外债比例的平均值来计算。k表示贸易方向约束系数,m表示外债方向约束系数,介于0和1之间。
将八种资产日收益、进口贸易比例以及外债结构比例数据代入MAD模型,用MATLAB软件进行计算。在满足短期外债和进口贸易支付的前提下,得出在绝对偏差最小时,我国外汇储备的资产结构如表2。
考虑我国贸易结构及外债结构,同时结合各资产的风险情况,我国外汇储备中日元所占比例最大为36.9%,其次为美元35.1%。这是因为日本和美国都是我国重要的贸易进口国,而且二者在我国外债中也占有重要地位。从绝对偏差模型的计算结果来看,日元、美元在我国外汇储备中占有重要地位。而欧盟虽然在近几年来一直是我国最大的进口国,但2009年以来的欧债危机导致欧元持续贬值,故欧元在外汇储备中仅占3.69%。单纯从绝对偏差模型来看,目前我国持有美元、欧元比重过高,应适当调低;日元比例应适当增加。
另外,均值、标准差并不被看好的澳元,计算结果表明在我国外汇储备中占比1.42%。这是由于我国的贸易结构约束所致。在我国对外贸易体系中,澳大利亚与中国贸易来往密切,并且由于其独特的地理位置与天然的资源优势,澳大利亚成为中国最主要的贸易进口国。因此,澳元应当成为我国战略外汇储备力量之一。
英镑占我国外汇储备0.28%的比例,初看起来不可思议。但仔细分析以后,可以发现英国同加拿大一样,都不是我国主要贸易进口国。同时英镑也并没有在外债货币种类中占有一席之地,故外债结构约束并不存在。
而在前面统计描述分析中,并不被看好的黄金和石油,也在外汇储备中占有一席之地。黄金在外汇储备中占比13.09%,居第三位;石油占比4.42%,居第五位。虽然最近黄金价格持续下跌,表现不良。鉴于黄金价格易受国际各方炒作的影响,伴随着价格的不稳定性,风险也就有所上升。但是相比较而言,黄金在一段时间内的浮动要比表现不良的货币小的多。同时作为真正的被世界各国所认可的资产,且又存在很少的政治风险,故有必要增持黄金。而石油作为我国的稀缺能源,对我国经济发展具有重要作用,即使石油价格具有较大的波动性,我国也有必要储备石油。
通过以上分析可以看出,通过绝对偏差模型计算的外汇资产结构具有一定的合理性,该模型估算的是长时期内外汇的最优结构,缺点是对风险度量没有考虑。接下来我们使用VaR方法对我国外汇结构进行进一步优化。
(五)我国外汇储备资产组合收益率统计特征
通过使用MAD模型计算出的各资产在我国外汇储备中所占的比重,可以计算出我国外汇储备资产组合的收益率,并对其进行统计分析(见表3)。
从表3可知,外汇储备资产组合的收益率均值为0.009 0,标准差为0.004 6。从标准差进行分析,可以明显看出外汇组合标准差0.004 6小于八种资产的标准差,表明我国外汇储备投资多种资产能很好地降低风险。
(六)基于GARCH模型计算我国外汇储备的VaR
在使用SAS软件对外汇储备资产组合进行GARCH建模前,先对组合收益率进行波动丛集性分析、平稳性检验、自相关检验、ARCH效应检验(异方差检验),证明数据为平稳非白噪声序列,残差序列具有显著的ARCH效应。在此基础上对组合收益率进行GARCH建模,计算不同分布假设下GARCH模型的参数。
结合上述分析,并运用AIC和SBC信息准则,经反复计算,判断阶数(p,q)为(1,1)比较合适。模型估计结果见表4。
表4参数检验结果显示,GARCH-N模型中,所有变量均显著,AIC准则为-10 316.337,SBC准则为-10 280.695,决定系数R2为0.453 1,可以认为模型拟合成功。GARCH-t模型中,所有变量均显著,AIC准则为-11 724.893,SBC准则为-11 684.159,决定系数R2为0.452 9,也可以认为模型拟合成功。而且从AIC准则和SBC准则考虑,在t分布假设下,GARCH模型拟合效果要优于正态分布假设。
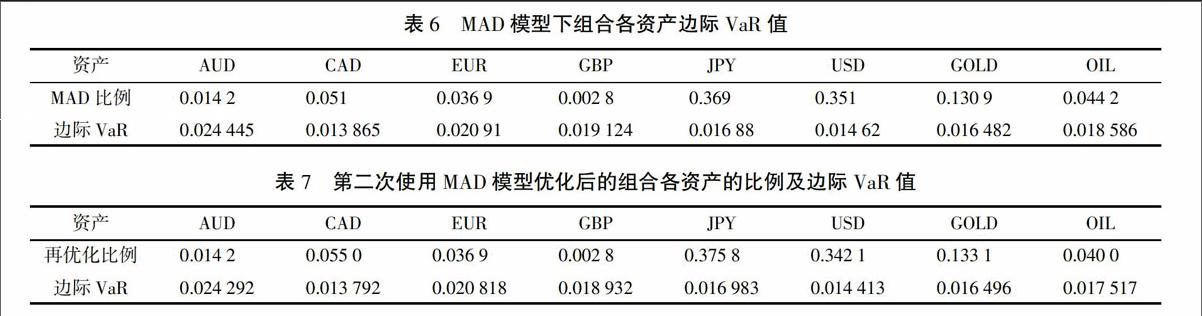
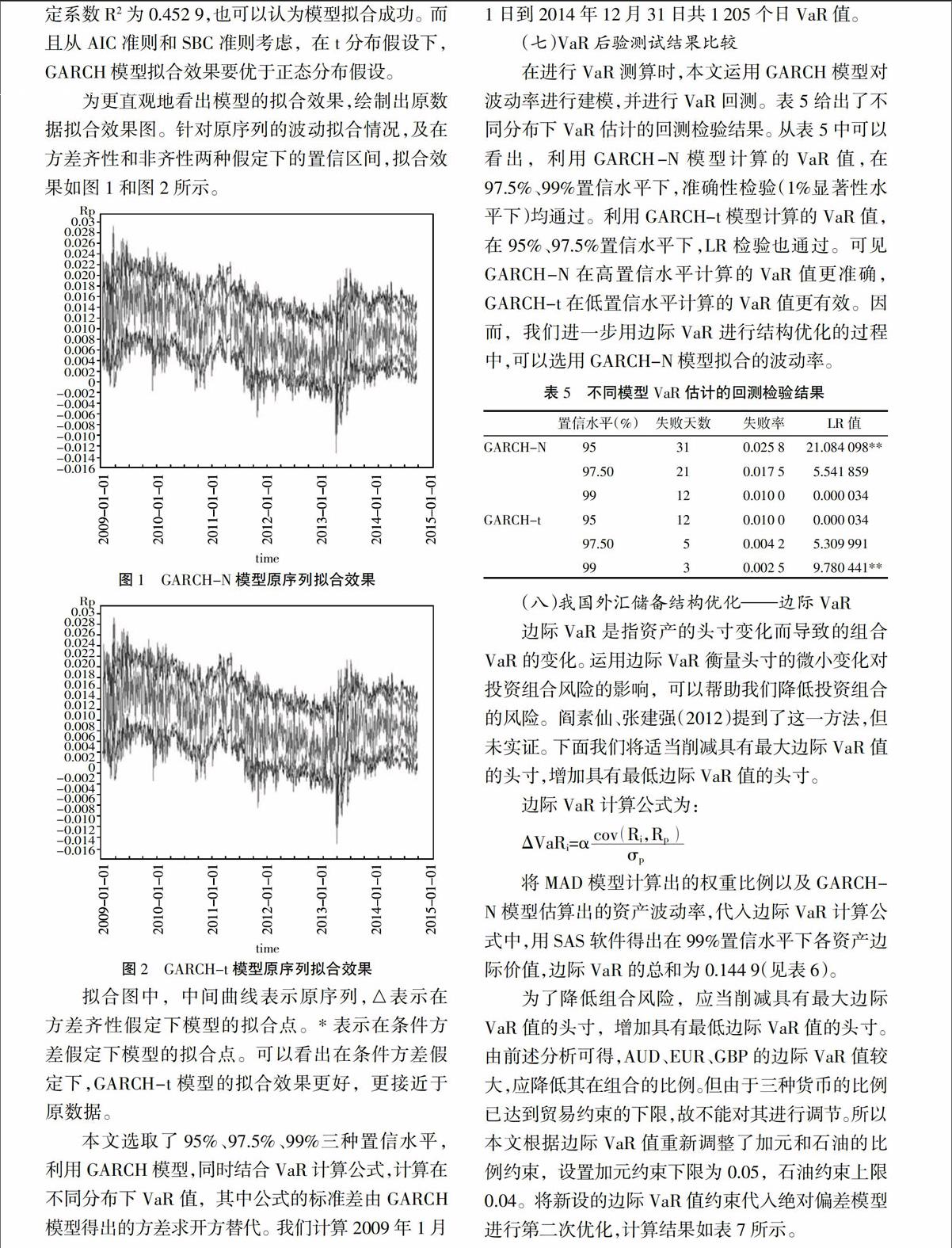
为更直观地看出模型的拟合效果,绘制出原数据拟合效果图。针对原序列的波动拟合情况,及在方差齐性和非齐性两种假定下的置信区间,拟合效果如图1和图2所示。
拟合图中,中间曲线表示原序列,△表示在方差齐性假定下模型的拟合点。*表示在条件方差假定下模型的拟合点。可以看出在条件方差假定下,GARCH-t模型的拟合效果更好,更接近于原数据。
本文选取了95%、97.5%、99%三种置信水平,利用GARCH模型,同时结合VaR计算公式,计算在不同分布下VaR值,其中公式的标准差由GARCH模型得出的方差求开方替代。我们计算2009年1月1日到2014年12月31日共1 205个日VaR值。
(七)VaR后验测试结果比较
在进行VaR测算时,本文运用GARCH模型对波动率进行建模,并进行VaR回测。表5给出了不同分布下VaR估计的回测检验结果。从表5中可以看出,利用GARCH-N模型计算的VaR值,在97.5%、99%置信水平下,准确性检验(1%显著性水平下)均通过。利用GARCH-t模型计算的VaR值,在95%、97.5%置信水平下,LR检验也通过。可见GARCH-N在高置信水平计算的VaR值更准确,GARCH-t在低置信水平计算的VaR值更有效。因而,我们进一步用边际VaR进行结构优化的过程中,可以选用GARCH-N模型拟合的波动率。
(八)我国外汇储备结构优化——边际VaR
边际VaR是指资产的头寸变化而导致的组合VaR的变化。运用边际VaR衡量头寸的微小变化对投资组合风险的影响,可以帮助我们降低投资组合的风险。阎素仙、张建强(2012)提到了这一方法,但未实证。下面我们将适当削减具有最大边际VaR值的头寸,增加具有最低边际VaR值的头寸。
将MAD模型计算出的权重比例以及GARCH-N模型估算出的资产波动率,代入边际VaR计算公式中,用SAS软件得出在99%置信水平下各资产边际价值,边际VaR的总和为0.144 9(见表6)。
为了降低组合风险,应当削减具有最大边际VaR值的头寸,增加具有最低边际VaR值的头寸。由前述分析可得,AUD、EUR、GBP的边际VaR值较大,应降低其在组合的比例。但由于三种货币的比例已达到贸易约束的下限,故不能对其进行调节。所以本文根据边际VaR值重新调整了加元和石油的比例约束,设置加元约束下限为0.05,石油约束上限0.04。将新设的边际VaR值约束代入绝对偏差模型进行第二次优化,计算结果如表7所示。
在进行第二次优化过程中,边际VaR的总和为0.143 2,组合标准差为0.004 625 9,而原组合的边际VaR的总和为0.144 9,标准差为0.004 640 5,这表明第二次优化后的组合风险有所下降。同时可以发现在新的约束条件下,我国外汇储备的结构应该是日元37.58%、美元34.21%、黄金为13.31%、加拿大元5.5%、石油为4%、欧元3.69%、澳元1.42%、英镑0.28%。
四、结论
本文通过两次使用绝对偏差模型计算外汇储备资产的最优配置比例,并使用VaR-GARCH模型进行配置资产的风险管理,进一步优化了我国外汇储备资产的结构,满足了外汇储备管理的安全性原则。本文从Wind数据库选取2009—2014年八种资产的日数据进行实证分析,得到如下结论:
1. 在最终配置中,日元占比最高为37.58%。日本作为中国邻国,两国经济贸易来往密切,同时日元具有相对较小的风险,建议适当增加日元在我国外汇储备中的比例。
2. 美元应占比34.21%。美国债务危机的发生,以及人民币对美元的不断升值,表明随着美元储备比例的提高,我国外汇储备的潜在损失也将提升。故应适当调低美元比例。
3. 黄金是世界货币金融体系中公认的价值基石,是硬财富的象征,建议我国在外汇储备中持有一定比例的黄金,合适的占比为13.31%。
4. 加拿大元在保证低风险的同时又具有较高的收益率,这是一个值得外汇储备投资的优良币种。建议我国外汇储备应提高加拿大元比重到5.5%。
5. 石油对一国经济的发展一直具有举足轻重的作用。针对我国石油依靠进口才能满足需求的现状,在外汇储备中应适当增加石油储备,实证结果表明石油占比4%较为合适,既能避免因国际油价波动对国内需求的影响,也能遏制其他国家通过石油来阻碍中国经济的发展。
6. 2009年以来的欧债危机导致欧元持续贬值,建议应降低欧元比例为3.69%。降低欧元比例也与最近一段时间世界各国减少欧元外汇储备规模的事实相一致。
在欧美债务危机不断发酵与国际金融环境持续动荡的大背景下,随着“一带一路”政策的顺利实施,我国未来国际政治经济战略和主要经济合作重心必将发生转移,也将会对我国外汇资产的币种结构带来一定的影响。本文实证给出了我国外汇储备的多元化的其他选择,如货币稳定表现良好的加拿大元,以及具有国际支付功能的黄金和战略储备资源石油等。
参考文献:
[1]Harry Markowitz.PortfolioSelection[J].The Journal of Finance,1952,(7):77-91.
[2]H.R.Heller,M.Knight. Reserve Currency Preferences of Central Banks[M].Essays in international Finance,1978:131-159.
[3]M.P. Dooley, J. Saul Lizondo, D. J. Mathieson.The Currency Composition of Foreign Exchange Reserves[J].IMF Staff Papers,1989,(2):385-434.
[4]Zong-Run Wang,Xiao-Hong Chen,Yan-Bo Jin,Yan-Ju Zhou. Estimating risk of foreign exchange portfolio:Using VaR and CVaR based on GARCH-EVT-Copula model[J].Physica A,2010,(21):4918-4928.
[5]Konno H,Yamazaki H.Mean-Absolute Deviation Portfolio Optimization Model and Its Application to Tokyo Stock Market [J].Management Science,1991,(37):519-529.
[6]姜昱,邢曙光.基于DCC-GARCH-CVaR的外汇储备汇率风险动态分析[J].财经理论与实践,2010,(164):16-20.
[7]阎素仙,张建强.中国外汇储备汇率结构风险研究 [J].河北经贸大学学报,2012,(1):25-34.
[8]余湄.我国外汇储备的风险管理问题研究[J].中国管理科学,2013,21(专辑):231-236.
[9]周光友,赵思洁.外汇储备币种结构风险测度及优化 [J].统计研究,2014,(3):68-75.
[10]王桐.我国外汇储备币种结构的优化研究[J].中国商贸,2015,(8):58-62.
[11]陈珂,徐丹萍,杨胜刚.基于风险选择与投资收益的外汇储备币种结构研究[J].财经理论与实践, 2015,(196):22-27.
责任编辑、校对:武玲玲
