黑土稻作水肥耦合对水分生产函数和产量的影响试验研究

金子茗，林彦宇，张玉庆，聂堂哲

(1.东北农业大学水利与建筑学院，黑龙江 哈尔滨 150030；2.东北农业大学农业部农业水资源高效利用重点实验室，黑龙江 哈尔滨 150030)



黑土稻作水肥耦合对水分生产函数和产量的影响试验研究

金子茗1，2，林彦宇1，2，张玉庆1，2，聂堂哲1，2

(1.东北农业大学水利与建筑学院，黑龙江 哈尔滨 150030；2.东北农业大学农业部农业水资源高效利用重点实验室，黑龙江 哈尔滨 150030)

摘要：为了探究水肥耦合对水分生产函数和水稻产量的影响，于2013年在庆安县和平灌溉试验站进行水稻田间试验，采用最优饱和D3-11设计方案，通过Jensen模型和回归模型进行数据分析、拟合方程，对水稻耗水规律和产量进行分析。结果表明：钾肥用量为95 kg/hm2，磷肥用量为100 kg/hm2，控制水稻分蘖后期土壤含水量下限值占饱和含水量的70%时，水稻可获得最佳产量。

关键词：水稻；水分生产函数；回归模型；水肥耦合

黑龙江省是粮食生产与输出大省，为保障全国粮食安全稳定贡献较大，但是黑龙江省又是水资源总量较少的省份，属于干旱半干旱气候区，水资源供需矛盾日益突出[1]，不合理施肥所造成的环境污染也日趋严重[2]。近年来对于水和氮肥，以及氮肥和钾肥耦合的研究备受关注，并在灌溉模式结合施氮肥对水稻产量影响规律[3]以及氮磷钾肥配合施用对水稻生长性状、产量影响规律[4]等方面的研究有了长足的进步。但对于水与磷钾肥耦合效应下耗水以及产量变化规律的研究则较少。本试验通过Jensen模型分析水稻不同生育期耗水量以及产量变化，利用回归模型分析水与磷钾肥耦合对水稻产量的影响。为农业生产合理灌水与施肥提供参考和依据。

1材料与方法

试验于2013年4月—9月在庆安县和平灌溉试验站进行。试验站位于绥化市庆安县，东经125°44′，北纬45°63′。试验区属于低山丘陵平原区，气候特征属寒温带大陆性季风气候，四季分明。多年平均气温为1.69℃，无霜期126 d左右，多年平均降雨量579 mm。试验地区为典型的寒地黑土，田间持水率39.61%，干密度1.10/cm3，有机质含量4.95%，全氮0.188%，全磷0.083%，试验选用品种为龙庆稻2号。氮肥选用尿素，磷肥选用二胺，钾肥选用硫酸钾。每个试验小区面积为100 m2，插秧密度为24穴/m2。

1.1试验方法

本试验采取饱和D3-11设计方案。采取三因素五水平，控制因素分别为控水下限(控制水稻分蘖后期土壤含水量下限值占土壤饱和含水量的比值)，磷肥与钾肥用量。试验共设11个处理，重复4次，水稻在整个生育期灌水标准为返青期统一控制田面水层为 0～30 cm，黄熟期自然落干，其它各生育期灌水以分蘖后期为基准，其比例关系为分蘖前期∶分蘖中期∶分蘖后期∶拔节孕穗前期∶拔节孕穗后期∶抽穗开花期∶乳熟期=1.3∶1.15∶1∶1.15∶1.3∶1.3∶1.15，另设一个对照组为充分灌水。采取随机区组排列。试验因素水平如表1所示。水稻于4月7日播种育苗，5月10日施基肥，5月23日进行插秧，6月5日施分蘖肥，7月15日施穗肥。施用农药1次。全生育期施肥标准如下：氮肥总量为300 kg/hm2，分3次施入，施肥比例为，基肥∶分蘖肥∶穗肥=4.5∶3∶2.5。磷肥总量作为基肥一次性施入。钾肥分两次施入，施入比例为，基肥∶穗肥=1∶1。

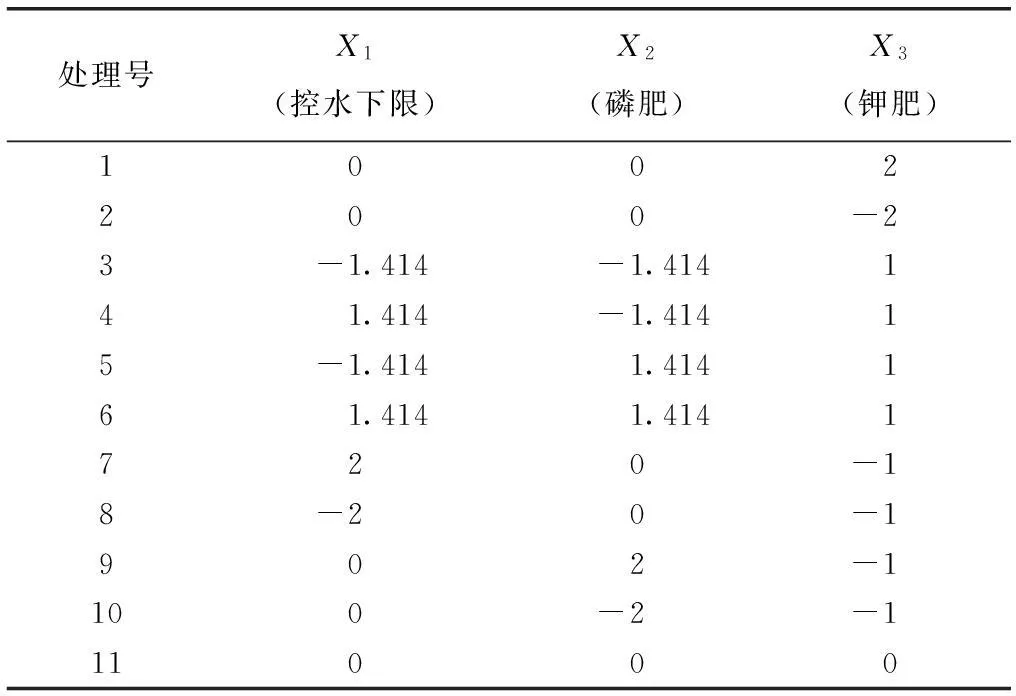
表1 试验因素水平表

注：0水平X1为70%，X2为75 kg/hm2，X3为100 kg/hm2；2平X1为80%，X2为150 kg/hm2，X3为200 kg/hm2；-2水平X1为60%，X2为0 kg/hm2，X3为0 kg/hm2。

1.2测定项目与方法

灌水量的测定：在土壤中水分含量达到试验方案的灌溉下限时进行灌水，记录灌水时间，灌溉水量。

水稻耗水量的测定：在田面有水层时通过水尺记录水层深度，没有水层时用土壤含水率测定仪确定土壤含水率，并与上一次测定的数值进行对比确定耗水量。

水稻各生育期生长性状的观测：在水稻各生育期记录水稻株数、分蘖数以及株高的变化。

水稻产量测定：水稻测定产量时，通过记录水稻有效穗数、每穗粒数和千粒重，计算理论产量。

1.3数据分析与处理

本试验数据采用Excel2010，SAS等软件进行处理。

2结果与分析

2.1水分生产函数模型的建立与求解

水分生产函数描述的是作物产量和灌溉水量之间的数学关系。本次试验分析不同土壤水分含量下限对水稻各生育期耗水量的影响，而在统计水分生产函数时，采用国内外公认比较合理和常用的Jensen模型进行数据分析，选水分生产函数静态模型中的相乘模型[5-7]。

Jensen模型表达式：

(1)

式中：λ为作物不同生育阶段对缺水导致产量降低的敏感指数；i为划分的生育阶段编号；Ym为充分灌溉条件下的产量；ETm为充分灌溉下的耗水量；Yα为实际灌溉条件下的产量；ETα为各处理的实际耗水量；n为划分的作物生育期阶段数，本次试验中为4。

试验选取分蘖期、拔节孕穗期、抽穗开花期，及乳熟期作为试验建立模型的阶段时期[8-9]，所得到的生育期耗水量以及最终水稻产量如表2所示，代入Jensen模型方程求得相应阶段的水分敏感指数与相关系数如表3所示。

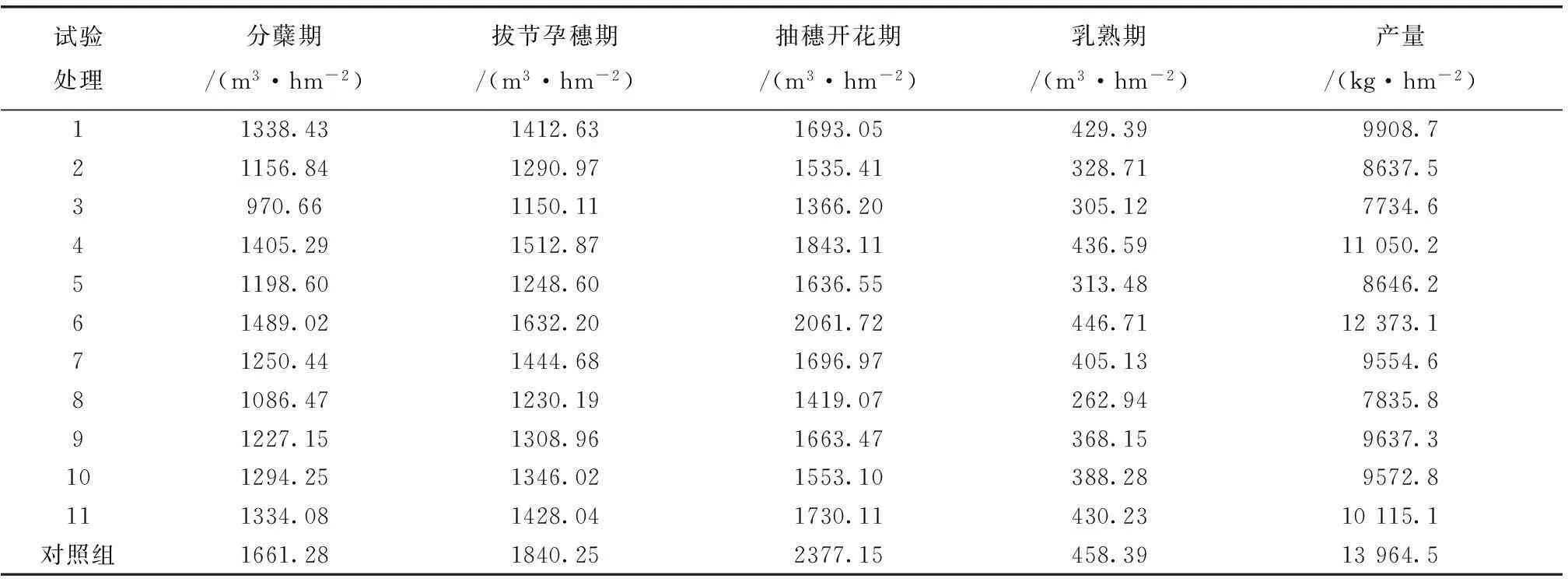
表2　选取生育期的耗水量及最终水稻产量

表3　试验生育阶段水分敏感指数以及相关系数

从表2可以看出，土壤水分含量对水稻各生育阶段的耗水量、水稻的产量的影响。在施肥量相同而土壤水分含量不同情况下，处理4比处理3的耗水量在分蘖期提高44.8%，拔节期提高31.4%，抽穗期提高34.9%，乳熟期提高42.9%，产量提高42.8%。处理6与处理5相比，耗水量在分蘖期提高24.2%，拔节期提高30.7%，抽穗期提高26%，乳熟期提高42.4%，产量提高43.1%。

土壤中的各种肥效均是通过溶于水分，由作物吸收而起到促进作物生长、提高产量的作用。适当提高土壤水分含量对水稻吸收养分、快速增长和增加产量有明显促进作用。

由表3可见，Jensen模型的水分敏感指数的顺序由大到小为：抽穗开花期>拔节孕穗期>分蘖期>乳熟期。Jensen模型的敏感指数表明该阶段对缺水的敏感程度，即敏感指数值愈大，缺水导致的减产愈严重。试验处理的相关系数为0.9879说明相关性较高，且各阶段敏感指数顺序和水稻的生长发育的生理需水特性相吻合。

通过Jensen模型的求解可知，水稻在不同生育阶段的缺水会对形成最终产量产生不同程度的影响。通过各生育期对缺水的敏感程度分析可以明确水稻的需水关键期。

2.2回归方程的建立

根据试验因素水平表(表1)和试验小区产量表(表2)，建立回归数学模型[10]，得到产量对土壤水分含量、磷肥和钾肥用量的回归方程。

Y=10 115+837.419X1+205.596X2+

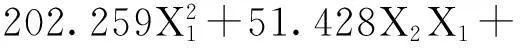
(2)

式中：Y为产量，kg/hm2；X1为分蘖后期控制土壤含水量下限，%；X2为磷肥用量，kg/hm2；X3为钾肥用量，kg/hm2。应用SAS软件对得到的试验数据进行分析，拟合方程，得出各因素对水稻产量影响的显著程度。

2.2.1主因子效应分析

由于式(2)中偏回归系数已标准化。通过式(2)中偏回归系数的绝对值大小可以判断各因子对产量影响的显著程度,系数正负号表示各因素对产量的提高是促进还是抑制。式中X1、X2、X3的系数为正，即控制水稻分蘖后期土壤含水量和施磷钾肥对水稻产量起到促进作用，促进作用的效果为：分蘖后期土壤含水量X1>钾肥X3>磷肥X2。方程交互项X1X2、X1X3、X2X3的系数为正，表明土壤含水量与磷肥，土壤含水量与钾肥，磷肥与钾肥耦合作用对产量起到促进作用。式中X1和X3的平方项为负数则表明，过多的土壤含水量、钾肥用量会抑制产量增加。

2.2.2耦合效应分析

令式(2)中一个因素编码值为零，可得到由另外两个因素所组成的二元二次方程。从式(2)可知，因素之间所表现出的交互作用，对产量影响的显著程度为：土壤含水量与钾肥交互>磷肥与钾肥交互>土壤含水量与磷肥交互。其中，土壤含水量与磷交互作不显著，暂不予考虑。

分析水和钾肥的交互作用，令式(2)中代表磷的编码值为零。得到土壤含水量和钾肥作用下产量效应方程。

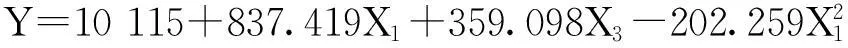
(3)

根据式(3)做土壤含水量和钾肥耦合作用水肥效应图，如图1所示。

图1　水与钾肥耦合效应图

从图1可看出，在土壤水分含量水平较低时提高钾肥施用量，随着钾肥用量的提高，产量呈现先增加后降低的趋势。即在较低土壤含水量时可获得较高产量，如土壤含水量编码值X1=-2、钾肥编码值X3=-1.414时，产量为7855.50 kg/hm2。而当土壤含水量编码值X1=-2、钾肥编码值X3=2时，产量为5876.41 kg/hm2。随着土壤水份含量提升而增加钾肥用量，产量表现为先增加后趋于稳定平缓。当再进一步提高土壤含水量时产量所能达到的最大值有所提高。即在较高的土壤含水量时施用钾肥能更有效提高产量，如土壤含水量编码值X1=0、钾肥编码值X3=1.414时，产量为10 210.88 kg/hm2。而当土壤含水量编码X1=2、钾肥编码值X3=1.414时，产量为12 220.71 kg/hm2。同样的当固定钾肥用量而改变土壤含水量时产量有相类似的变化。

当同时改变土壤含水量和钾肥用量时，产量的变化会更加显著。当土壤含水量编码值X1=-2、钾肥编码值X3=-2时，产量为7701.70 kg/hm2。同时增加土壤含水量和钾肥用量，会使产量明显提高，如土壤含水量编码值X1=2、钾肥编码值X3=2时，产量为12 487.84 kg/hm2。

2.2.3数学模型寻优

最佳产量优化方案由式(2)分别对X1，X2，X3求偏导，得到方程组(4)～(6)，并求解方程组。

∂y/∂X1=837.419-404.518X1+

51.428X2+407.719X3=0

(4)

∂y/∂X2=205.596+51.428X1+

50.406X2+189.471X3=0

(5)

∂y/∂X3=359.098+407.719X1+

189.471X2-421.016=0

(6)

解方程组得X1=0.669、X2=-5.08、X3=-0.1，即在土壤水分含量下限为70%、钾肥95 kg/hm2、而磷肥在试验中没有对应的编码值，且磷肥对水稻产量影响不显著，根据当地生产实践选用磷肥用量100 kg/hm2，在这种土壤水分含量、磷钾肥用量水肥组合时，水稻可获得最佳产量。

3结论

(1)通过Jensen模型进行数据处理，得出各生育期的缺水敏感指数，由大到小为：抽穗开花期>拔节孕穗期>分蘖期>乳熟期。提高土壤水分含量下限，对促进水稻各生育期耗水量、水稻最终产量有十分显著的影响，

(2)通过对回归方程进行拟合，并对模型寻优可得到：在水稻分蘖期控制土壤水分含量下限为土壤饱和含水量的70%、钾肥95 kg/hm2、磷肥用量100 kg/hm2的水肥组合时，可获得最佳产量。

(3)在Jensen模型水分生产函数分析的基础上，通过回归方程进行分析水肥耦合作用对水稻产量的影响。由于在水肥耦合组合中水与钾肥耦合作用显著，所以进行主要分析。得出结论：在确定土壤水分含量下限时应注意钾肥施用量，而施用钾肥的量也根据土壤水分含量下限高低确定。不合理搭配土壤水分含量和钾肥用量达不到高产的目的，甚至会造成产量的减少，浪费水资源和肥料，造成生态破环。只有合理进行土壤水分含量、磷钾肥的用量组合才能达到水肥耦合最佳效果，获得最佳产量，并根据作物在不同生育期的对缺水敏感程度，合理灌水，达到水肥资源的高效利用。

参考文献：

[1]王克全，付强.黑龙江省西部半干旱区水稻水分生产函数及优化灌溉制度研究[J].节水灌溉，2007(8):48-51.

[2]赵瑞龙，周明耀，顾玉芬,等.水稻水肥耦合技术生态环境效益和最佳模式研究[J].水利与建筑工程学报，2005,3(4)：18-20.

[3]肖新，朱伟.灌溉模式与施氮量对水稻需水规律及产量的影响[J].南京农业大学学报，2012，35( 4)：27-31.

[4]陈燕，王代平.氮磷钾肥配合施用对水稻生长状况及产量的影响[J].现代农业科技，2013(13)：34-36.

[5]缴锡云,雷志栋.非充分灌溉制度对Jensen模型的敏感性分析[J].灌溉排水学报，2005，24(2):10-12.

[6]付强，王立坤.三江平原井灌水稻水分生产函数模型及敏感指数变化规律研究[J].节水灌溉，2002(4):1-3.

[7]王克全，付强.查哈阳灌区水稻水分生产函数模型及其应用试验研究[J].灌溉排水学报,2008，27(3):109-111.

[8]季飞，付强.不同水分条件对水稻需水量及产量影响[J].灌溉排水学报,2007，26(5):82-85.

[9]孙艳玲，李芳花.寒地黑土区水稻水分生产函数试验研究[J].灌溉排水学报,2010，29(5):139-142.

[10] 尹光华，刘作新.辽西半干旱区春小麦氮磷水耦合产量效应研究[J].农业工程学报,2005，21(1):41-45.

Experimental study on the influence of water-fertilizer coupling on water production function and yield of rice planted in black soil

JIN Ziming1，2，LIN Yanyu1，2，ZHANG Yuqing1，2，NIE Tangzhe1,2

(1.WaterConservancyandArchitectureCollege,NortheastAgiculturalUniversity，HarbinHeilongjiang150030,China;2.KeyLaboratoryofEfficientUtilizationofAgriculturalWaterResources，MinistryofAgriculture,NortheastAgricultureUniversity,Harbin150030,China)

Abstract：In order to explore the influence of water and fertilizer coupling on water production function and yield of rice，field experiment was carried out in Helping irrigation station of Qing'an county in 2013. Through the application of the optimal saturation D3-11 design, data analysis and equation fitting were performed with Jensen Model and regression model and the water consumption regulation and yield of rice were analyzed. The results showed that the rice yield reached optimal value with the potash fertilizer of 95 kg/hm2, phosphatic fertilizer of 100 kg/hm2, and soil moisture limit at final tillering stage of 70%.

Key words：rice;water production function;regression model;water-fertilizer coupling

基金项目：“十二五”国家科技支撑计划(2012BAD08B05)

作者简介：金子茗(1988-)，男，硕士研究生，研究方向为农业节水理论与技术。E-mail：jzm_88@qq.com

中图分类号：S275

文献标志码：A

文章编号：2096-0506(2015)02-0001-04