GM(1,1)模型优化及在地下水位预测中的应用
2016-06-15孙新新黄一彬
孙新新,黄一彬
(温州市水利局,浙江 温州 325000)
GM(1,1)模型优化及在地下水位预测中的应用
孙新新,黄一彬
(温州市水利局,浙江 温州 325000)
摘要:地下水水位变化特征是研究区域地下水的基础,采用优化GM(1,1)模型对温州市永强平原地下水水位进行模拟和预测,优化模型后验差比值和平均相对误差均明显低于GM(1,1)模型,表明优化模型在预测精度上有很大提高,可靠性更好,为地下水水位预测提供了一条新途径。
关键词:灰色理论;GM(1,1);优化模型;温州市;永强平原;地下水水位预测
地下水水位变化特征是研究区域地下水的基础,也是衡量地下水资源量及开采量的重要指标。过度开采地下水易造成地面沉降,不易治理且影响持久;沿海地区还可能导致海水入侵,地下淡水盐碱化。因此,合理预测地下水水位不仅可以了解区域地下水变化趋势,同时也为地下水开发利用及管理提供科学指导。目前用于地下水水位预测的方法很多,大致分为两类,确定性方法和随机性方法[1]。确定性方法主要通过地下水运动微分方程和定解条件建立模型来求解,包括解析法、数值法等;随机性方法通过建立影响因素与预报因子之间的函数关系来实现,具有更多的灵活性[2],如线性回归分析法、频谱分析法、时间序列法、模糊理论、灰色理论、神经网络,以及遗传算法等[2-7]。
地下水水位受降水、径流、蒸发、植被,以及开采等诸多因素影响,确定性预测方法对资料精度要求高,参数复杂,计算量大,故本文采用随机性方法中的灰色理论。灰色GM(1,1)模型是基于灰色系统理论的一种预测方法[8],具有对历史样本数量要求少,计算简便,验证方便等优点,在很多领域得到广泛应用[9-11]。灰色GM(1,1)模型对于原始数据波动小的单调递增或递减的序列,预测精度较高,若原始数据波动较大,则预测值的误差就比较大。本文对GM(1,1)模型进行优化,采用指数函数和线性函数联合模拟,弥补了原模型对于序列线性因素考虑的不足,并采用优化模型对温州市永强平原地下水水位进行预测,结果较理想。
1GM(1,1)模型的原理和方法
1.1模型建模
初始非负序列X(0),X(0)=(x(0)(1),x(0)(2),…x(0)(n)),对其作1-AGO变换,一次累加生成序列X(1),X(1)=(x(1)(1),x(1)(2),…x(1)(n)),其中,
(1)
紧邻均值序列Z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),其中z(1)(k+1)是[k,k+1]区间内dx(1)/dt的背景值,见式(2)。

(2)
(3)

对影子方程进行求解,得到时间响应方程,即GM(1,1)模型如下:

(4)
1.2模型检验

2模型的优化
在GM(1,1)模型的基础上,采用线性函数和指数函数进行联合模拟预测,设:
(5)
式中:a为发展系数,通过公式(3)计算而得,利用最小二乘法求解系数b1、b2、b3。设:
(6)

3优化灰色GM(1,1)模型的应用
温州市地处浙东沿海,永强平原位于瓯江河口和飞云江河口之间的滨海平原,人口密集,民营经济发达,是温州机场所在地。由于多年过度开采地下水,部分地区多处产生地面沉降,2005年随着温州地下水禁、限采等措施的出台,地下水水位逐渐回升。研究选取永强平原海滨水厂2005—2014年的地下水水位(由温州市地质环境监测站提供)如表1所示,利用2005—2011年数据建模,2012—2014年数据作为验证,并对2015—2016年地下水水位进行预测。
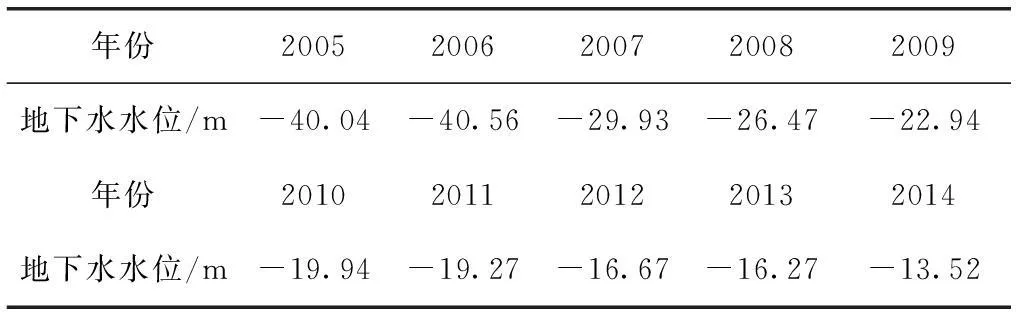
表1 五溪沙站2005—2014年地下水水位表
由于地下水水位均为负值,首先原序列进行非负处理,所有数据均取其绝对值,形成初始序列为X(0)=(40.04,40.56,29.93,26.47,22.94,19.94,19.27),并进行累加,生成新序列X(1)=(40.04,80.6,110.53,137,159.94,179.88,199.15)。
3.1GM(1,1)模型预测
紧邻均值序列Z(1)=(60.32,95.565,123.765,148.47,169.91,189.52),根据公式(3)计算得到,a=0.160 709,u=47.612 629,则
-256.225 621e-0.160 709k+296.265 621,
累减反算出原始序列估计值,再对数据取负,得到地下水水位预测值及误差,详见表2所示,模型精度见表3所示。
3.2优化GM(1,1)模型预测

根据公式(6)计算得到
则:
7.614 431k+207.836 561
(7)
累减反算出原始序列的估计值,再对数据取负,得到地下水水位预测值及误差如表2所示,模型精度如表3所示。

表2 地下水位预测结果

表3 模型精度
由表2和表3可知,从总体上看,两种模型的后验差比值均小于0.35,小误差概率均大于0.95,精度均为一级,但是优化模型后验差仅为原模型的50.5%,且其预测值多数较原模型的误差小,更接近实测值。优化模型建模期和验证期预测相对误差均值分别为3.8%和3.7%,分别是原模型的80.6%和18.7%,预测的精度大大提高。因此,优化后的模型更适用于温州永强平原地下水水位的短期预测。
3.3未来地下水水位预测
把k=10,k=11带入公式(7),并进行累减、取负,可得到2015年和2016年地下水水位,结果见表4。
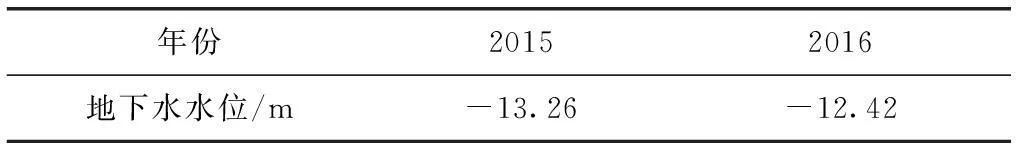
表4 2015—2016年地下水水位预测结果表
4结语
(1)影响地下水水位的因素很多,确定性方法预测复杂。优化的GM(1,1)模型保持了GM(1,1)模型对序列长度要求低、计算方便的优点,同时将指数函数和线性函数组合代替单一的指数函数,弥补了原模型没有考虑线性因素的不足。
(2)无论在建模阶段,还是在验证阶段,优化的GM(1,1)模型预测值的相对误差都较原模型小,数据更加接近实测值。通过精度检验,优化后的模型后验差比值为0.109,平均相对误差3.8%均优于GM(1,1)模型,尤其是在验证期,优化模型平均相对误差仅为原模型的18.7%,表明优化的GM(1,1)模型较原模型精度明显提高。
(3)优化模型的精度检验验证了该模型在温州市永强平原地下水水位预报应用中的适应性和合理性。根据优化后的模型预测出2015年和2016年温州市永强平原地下水水位分别为-13.26 m和-12.42 m。
(4)优化后的GM(1,1)模型虽然大大提高了预测精度,但是仍无法改变模型递推性有限的缺陷,模型的精度和建模期、验证期序列的长度有较大关系,该优化模型是否可以用于进行温州永强平原地下水的中长期预测,还需要进一步验证。
参考文献:
[1]陈葆仁,洪再吉.地下水动态及其预报[M].北京:科学出版社,1988.
[2]王新民,崔巍.变权组合预测模型在地下水水位预测中的应用[J].吉林大学学报:地球科学版,2009,39(6):1101-1105.
[3]孙雪,王小松,程莉蓉,等.时间序列模型在北京西山地区岩溶地下水文预测中的应用[J].水资源与水工程学报,2014,25(3):161-164.
[4]金菊良,丁晶,魏一鸣.基于遗传算法的门限自回归模型在浅层地下水位预测中的应用[J].水利学报,1999(6):51-55.
[5]张斌,刘俊民,张博炜,等.灰色神经网络在地下水动态预测中的应用[J].中国农村水利水电,2013(1):5-10.
[6]吴丽萍,朱长军,李莎.灰色预测在地下水位预测中的应用[J].地下水,2012,34(2):66-68.
[7]周维博,李娜,刘雷,等.基于自适应神经模糊推理系统的地下水预测[J].水土保持通报,2014,34(4):138-140.
[8]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010.
[9]彭正明,王腾军,曹冬冬,等.GM(1,1)模型的改进及其在变形预测中的应用[J].地球科学与环境学报,1995,34(4):102-106.
[10] 张琼楠,张龙.改进的灰色GM(1,1)模型在农业需水预测中的应用[J].三峡大学学报,2013,35(6):12-15.
[11] 徐步然.灰色GM(1,1)模型在能源消费预测中的应用[J].重庆理工大学学报,2014,28(9):130-133.
[12] 邓聚龙.灰色系统理论基本方法[M].武汉:华中科技大学出版社,2005.
The optimization of Grey GM(1,1) model and it’s application on the prediction of groundwater level
SUN Xinxin,HUANG Yibin
(WaterConservancyBureauofWenzhouCity,Wenzhou325000,China)
Abstract:Variable characteristics of groundwater level is fundamental for local groundwater research.The optimized GM(1,1) model was adopted to stimulate and predict groundwater level in Yongqiang plain of Wenzhou city. The posterior error ratio and the average relative residual error ratio of optimized grey GM(1,1) were significantly lower than those of GM(1,1) model,which showed that the prediction accuracy and reliability of optimized model were improved significantly. The optimization of Grey GM(1,1) model and its application provided a new method for the groundwater prediction.
Key words:theory of grey system;GM(1,1);optimized model;Wenzhou city;Yongqiang plain;groundwater level prediction
作者简介:孙新新(1982-),女,工程师,研究方向为水文水资源、河道管理。E-mail:sunxx1216@126.com
中图分类号:P641.7
文献标志码:A
文章编号:2096-0506(2015)02-0031-04
