基于非均匀B样条的拉曼光谱基线校正算法

范贤光， 王海涛， 王 昕， 许英杰， 王秀芬， 阙 靖

厦门大学物理与机电工程学院， 福建 厦门 361005

基于非均匀B样条的拉曼光谱基线校正算法

范贤光， 王海涛， 王 昕*， 许英杰， 王秀芬， 阙 靖

厦门大学物理与机电工程学院， 福建 厦门 361005

基线校正是一种常用的消除光谱荧光干扰的方法， 是拉曼光谱数据处理的必要步骤之一。 传统的多项式拟合基线校正算法， 简单且易于实现， 但是拟合阶次难以确定， 灵活性较差。 使用非均匀B样条代替多项式进行拟合， 在保留原有算法优点的基础上， 利用原始拉曼谱图的峰位置信息自适应地确定非均匀B样条的节点向量， 然后以固定阶次拟合光谱基线。 B样条自身具有分段光滑的特性， 而计算样条节点的节点向量自适应选取算法中的峰位置信息通过使用两次具有不同母函数的连续小波变换(continuous wavelet transform, CWT)来获取， 既加强了原始光谱数据与B样条算法本身的联系， 也克服了传统多项式拟合的不足。 为了验证本文算法的有效性， 选取了甲基对硫磷和某品牌菜籽油两种被测物进行实验， 并使用该算法进行了基线校正， 并与两种其他的基线校正算法与进行了对比。 实验结果表明， 该方法利用固定的拟合阶次就能达到较好的校正效果， 所需要的参数较少， 校正结果不会出现过拟合或欠拟合的现象， 是一种有效的拉曼光谱基线校正算法。

拉曼光谱； 基线校正； 非均匀B样条； 节点向量； 峰位置

引 言

拉曼光谱(Raman spectroscopy)作为一种鉴定物质结构的分析测试手段， 广泛应用于材料、 化工、 石油、 高分子、 生物、 环保、 地质等领域[1]。 由于荧光干扰等因素的存在， 光谱往往会发生较大漂移[2]， 因此， 需要通过一定的方法对拉曼光谱进行基线校正。

目前， 主要的基线校正的方法有多项式拟合[3]、 小波变换[4]、 求导[5]等方法。 多项式拟合是最常用的基线校正算法， 通常使用最小二乘法， 通过循环迭代获得拉曼光谱的基线。 此方法易于实现， 但精度不高， 当谱峰较多时， 拟合阶次难以确定， 容易出现过拟合， 并且由于没有考虑局部性， 当某些数据点漂移时， 会影响整体拟合效果。

小波变换法利用小波变换对原始光谱进行分解， 对于分解到小波域的信号， 采取低频置零， 高频阈值过滤的操作， 截取到的有用信号再进行重构。 此方法的前提条件是， 基线相对于原信号是变化缓慢的低频信号， 基线和光谱特征峰的频率有明显界限。 此外， 小波函数的选取和变换尺度都较难确定， 且对校正效果的好坏有直接影响。 求导的方法遵循小波变换法“信号分解-信号处理-信号重构”这样的处理原则， 但是校正基线后， 会改变原始光谱的形状。

针对以上问题， 本文提出一种基于非均匀B样条的基线校正方法， 利用小波变换寻峰算法自适应地确定非均匀B样条的节点向量， 并使用固定阶次的非均匀B样条， 通过循环迭代拟合基线， 从而达到较好的基线校正效果。

1 理 论

1.1 非均匀B样条拟合

B样条方法以其低阶光滑的特性， 被广泛的应用于自由曲线曲面的造型中[6-7]。 B样条的曲线方程为

(1)

其中，di(i=0, 1, …,n)表示第i个控制系数， B样条曲线的控制多边形就是由这些控制点依次连接而成。Ni, k(u)(i=0, 1, …,n)表示第i个k次(k+1阶)B样条基函数， 定义为

(2)

其中，ui称为节点， 它是节点向量U={u0,u1, …,un}这个单调非减集合的一个元素。 定义域被节点细分为一个个的节点区间。 如果这些节点区间是均匀的， 则称使用这些节点的B样条曲线为均匀B样条曲线， 否则， 称之为非均匀B样条曲线。 计算一条k次B样条曲线， 由方程(1)可知， 共需n+1个控制系数di(i=0, 1, …,n)以及n+1个k次B样条基函数。 控制系数一般通过最小二乘法获得[8]， B样条基函数则利用节点向量通过式(2)获得。 因此， 节点向量对于计算整个B样条曲线有着非常重要的作用， 节点的分布直接影响B样条算法的拟合效果。

1.2 节点向量自适应选取方法

拉曼光谱基线变化较大的位置一般发生在拉曼光谱的谱峰位置附近， 因此本文初步选取峰位置点作为B样条算法的节点。 文献[9]提出了一种利用连续小波变换实现拉曼谱峰识别的方法， 本文利用该方法获得拉曼光谱的谱峰位置， 进而获得非均匀B样条节点向量。 小波变换是一种利用小波把信号从时域转换到小波域的手段, 素有“数学显微镜”的美誉[10-11]。 连续小波变换的数学表达式可以定义为

(3)

其中，s(t)是原信号，a为尺度因子，b为时间平移因子，Ψa, b(t)是小波母函数，C(a,b)为小波变换系数， 表示不同尺度不同时间平移下小波函数的线性组合。 小波系数表示了选定小波母函数与处于特定时移b和特定尺度a下与原信号的相似度。 谱峰识别的算法中， 选取墨西哥帽小波作为小波母函数

(4)

使用墨西哥帽小波作为小波母函数， 对拉曼信号进行连续小波变换后， 在每个尺度a上的小波系数， 靠近峰中心位置附近时， 会出现模极大值。 并且这个模极大值随尺度的变化而变化， 当小波变换尺度与原谱峰峰形最匹配时， 模极大值达到最大。 将小波系数中的模极大值连接起来， 则形成如图1所示的脊线。 该图的横坐标为拉曼位移， 纵坐标为连续小波变换尺度。 那些又长并且由较大的模极大值连接成的脊线就是较大的谱峰的位置。 由于噪声的存在， 最初检测到的谱峰会混杂有假峰， 因此， 需要对假峰进行剔除处理。 文献[12]介绍了谱峰位置检测的大量准则， 如信噪比、 脊线、 模极大值和峰宽等。 本文中的峰位置检测按照基于信噪比和脊线的方法， 其中信噪比用来剔除假峰， 脊线长度阈值用来提取较大的峰位置。

获得所有谱峰位置后， 其峰位置点P=[p0,p1, …,pn]还需进行进一步的处理， 才能作为非均匀B样条的节点。 这是由于为保证B样条拟合的效果， 其节点的分布不宜过密， 也不宜过稀。 过密的节点分布， 一方面增加拟合的计算量， 另一方面容易导致过拟合； 而过稀疏的节点分布， 容易导致欠拟合。 为保证节点的合理分布， 设定两个参数d1和d2， 对峰位置P=[p0,p1, …,pn]进行处理， 从而确定B样条节点向量。

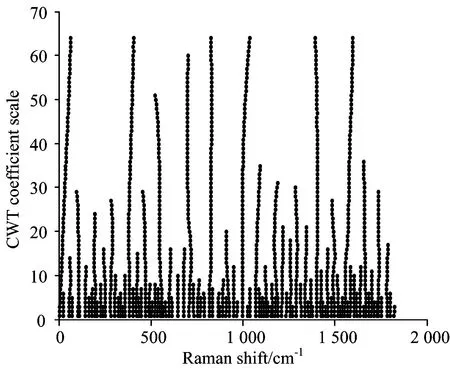
Fig.1 Identified ridge lines based on CWT coefficient image

节点向量的获取方法可分为以下几个步骤：

(1) 使用墨西哥帽小波作为母函数对原拉曼信号进行连续小波变换；

(2) 连接不同尺度下的模极大值序列， 构建脊线， 具体参考文献[9]；

(3) 根据参考文献[13]的方法剔除假峰， 得到最终的峰位置向量P=[p0,p1, …,pn]；

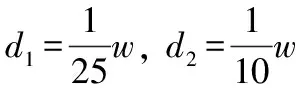
(5) 处理后的峰值点向量P赋值给U， 作为非均匀B样条的节点向量。

1.3 非均匀B样条基线校正的实现

本文利用改进的寻峰算法确定非均匀B样条的节点向量， 然后利用非均匀B样条循环逼近曲线基线， 原始光谱扣除基线后， 即得到基线校正后的曲线。 非均匀B样条基线校正算法的原理可由图2表示， 整个算法的基本步骤如下：

(1) 采样获得m个点构成的原始光谱数据S0， 令y0=S0；

(2) 使用1.2节节点确定算法计算非均匀B样条节点向量U；

(3) 对y0使用4阶(3次)非均匀B样条拟合， 得到yn作为初次拟合的基线；

(4)yn与y0逐点比较， 取较小的点赋值给yn；

(5)yn与y0的相对误差若小于迭代阈值ζ， 则判定yn为光谱曲线的基线， 否则， 令y0=yn， 返回步骤3继续执行， 直到满足条件为止；

(6) 校正后的光谱数据Scorrect=S0-yn。

Fig.2 Process of baseline correction by Non-Uniform B-spline fitting

2 实验部分

2.1 材料及仪器

本文所选取的被测物质是浓度为10 ppm的甲基对硫磷和浓度为10 ppm某品牌菜籽油。 所使用的实验仪器为Ocean Optics公司的QE65Pro。

2.2 结果分析

利用本文算法对甲基对硫磷(parathion-methyl， PM)和菜籽油(colza oil， CO)进行处理， 两种物质的原始拉曼谱图和拟合出的基线如图3所示。 其中， 峰值检测算法参数为： 小波变换尺度scales=1∶70, 剔除脊线的参数SNR=5和ridgeLength=10， 得到的峰值点分别为

PPM=[481, 614, 730, 828, 913, 1 006, 1 076, 1 196, 1 275, 1 357, 1 433, 1 505, 1 646, 2 370]

PCO=[390, 840, 972, 1 093, 1 255, 1 292, 1 436, 1 655, 1 736, 1 869, 1 889, 1 941, 1 975, 2 025, 2 087, 2 146, 2 183, 2 235, 2 342, 2 403]

选取的循环迭代阈值ζ=0.5， 非均匀B样条拟合阶数为4。 按照上述给定参数， 根据本文算法拟合出的甲基对硫磷和菜籽油的拉曼谱图的基线如图3所示。 由图3(a)可以看出， 本文所测的甲基对硫磷的拉曼谱图在1 000～1 500 cm-1附近峰的分布较密， 拉曼位移从1 700～2 500 cm-1没有明显的拉曼峰。 根据峰值检测算法计算出的甲基对硫磷的峰值点PPM， 峰值较密附近存在多达7个峰值点， 1 700～2 500 cm-1仅有1个峰值点， 因此PPM不能直接作为B样条节点向量， 需要对PPM进行进一步处理。

根据节点向量自适应选取方法得到参数d1=100，d2=250， 则处理后的非均匀B样条节点为

UPM=[481, 614, 730, 913, 1 196, 1 357, 1 505, 1 646, 1 846, 2 180, 2 370]

UCO=[390, 615, 840, 972, 1 093, 1 255, 1 436, 1 655, 1 869, 1 975, 2 087, 2 161, 2 235, 2 342]

处理后的B样条节点向量UPM， 节点分布合理， 得到的校正基线也较为平滑， 没有在峰位置过密的1 000～1 500 cm-1区域出现过拟合， 也没有在峰值点较少的1 700～2 500 cm-1上出现欠拟合。 校正后的甲基对硫磷的拉曼光谱图如图4(a)所示。 本文算法在进行基线校正时， 并没有对原始拉曼数据进行平滑去噪等预处理操作， 图3(b)为实验所测的菜籽油的拉曼谱图， 箭头标示处存在高频噪声， 对比图4(b)菜籽油基线校正后的拉曼谱图， 可以发现菜籽油的谱图的高频噪声处基线拟合依然平滑， 校正后的谱图也没有发生过拟合的现象， 证明了本算法的有效性。

Fig.3 Raman spectroscopy and its baseline by Non-Uniform B-spline fitting

选取传统多项式拟合算法与改进的惩罚最小二乘算法[13]与本文算法进行比较。 图5给出了使用5阶多项式拟合的基线校正算法所得出的菜籽油拉曼谱图及其校正基线。 所

Fig.4 Raman spectroscopy after baseline correction by Non-Uniform B-spline fitting

Fig.5 Raman spectroscopy and its baseline by polynomial fitting of colza oil

测得的菜籽油拉曼谱图漂移较大， 且存在高频噪声， 利用5阶多项式拟合菜籽油基线时， 800 cm-1处开始的基线出现明显的过拟合现象， 1 800 cm-1处又出现欠拟合现象。 图6为利用改进的惩罚最小二乘法获得的甲基对硫磷的校正基线及其校正后的拉曼谱图。 文献[13]将该方法做成了R语言开源包baselineWavelet。 该方法先利用两个小波变换获取峰的信息， 然后在峰位置处使用直线连接峰首尾作为基线， 非峰部分使用惩罚最小二乘法拟合基线， 拼接后得到最终基线。 此方法计算出的基线与原始谱图结合紧密， 不易出现过拟合的现象。 但是， 由于基线是两种方法拼接而成， 该方法的基线整体不够平滑， 如图6(a)所示。 比较图4(a)和图6(b)， 本文算法与改进的惩罚最小二乘算法校正效果差别不大， 但是， 此方法相较于本文算法， 默认参数众多， 两次小波变换计算量也较大。

Fig.6 Raman spectroscopy of parathion-methyl

(a): Raman spectroscopy and its baseline; (b): Raman spectroscopy after baseline correction by baseline wavelet

综上所述， 采用基于非均匀B样条的基线校正方法， 充分利用了B样条的低阶光滑特性， 克服了传统多项式基线校正算法拟合阶数难确定的缺陷， 在基线偏移严重和存在高频噪声时， 仍能够拟合出光滑的基线， 并没有出现欠拟合和过拟合的现象， 对于存在基线漂移的拉曼光谱信号， 达到了较好的基线校正效果。

3 结 论

提出了一种基于非均匀B样条的拉曼光谱基线校正方法， 先利用基于小波的谱峰识别算法获得拉曼谱图的峰位置， 然后对这些峰位置点进行处理， 从而确定出非均匀B样条的节点向量， 最后利用B样条以固定的阶次循环迭代拟合拉曼谱图的基线。 与传统的多项式拟合算法相比， 本文的自适应节点确定算法充分利用了不同拉曼谱图的信息， 让拟合出的基线与原始拉曼谱图结合更紧密； 同时， 本文的方法能够以固定的阶次拟合光谱基线， 并且能够有效地避免过拟合和欠拟合。 因此， 本文所提出的方法， 能够较好地实现拉曼光谱的基线校正， 并且调整参数少、 易于实现， 可以作为一种有效的拉曼光谱基线校正算法。

[1] CHU Xiao-li(褚小立). Molecular Spectroscopy Analytical Technology Combined with Chemometrics and Its Applications(化学计量学方法与分子光谱分析技术). Beijing: Chemical Industry Press(北京： 化学工业出版社), 2011. 311.

[2] McCreer R L. Raman Spectroscopy for Chemical Analysis. Wiley-Interscience, 2000.

[3] FENG Xin-wei, ZHU Zhong-liang, SHEN Meng-jie, et al. Computer and Applied Chemsity, 2009, 26(6): 759.

[4] Jagtiani A V, Sawant R, Carletta J. Measurement Science and Technology, 2008, 19(6): 1.

[5] O’Grady A, Dennis AC, Denvir D. Analytical Chemistry, 2001, 73: 2058.

[6] Piegl L, Tiller W. The NURBS Book(非均匀有理B样条). Translated by ZHAO Gang, MU Guo-wang, WANG La-zhu(赵 罡， 穆国旺， 王拉柱， 译). Beijing: Tsinghua University Press(北京： 清华大学出版社), 2010. 60.

[7] GUO Jian-feng, ZHU Chang-qing(郭建峰， 朱长青). Engineering of Surveying and Mapping(测绘工程)， 2000, 9(4): 25.

[8] SHI Fa-zhong(施法中). CAGD & NURBS(计算机辅助几何设计与非均匀有理B样条). Beijing: Higher Education Press(北京： 高等教育出版社), 2013. 303.

[9] Du P, Kibbe W A, Lin S M. Bioinformatics, 2006, 22: 2059.

[10] Daubechies I. Ten Lectures on Wavelets(小波十讲). Translated by LI Jian-ping(李建平， 译). Beijing: National Defense Industry Press(北京： 国防工业出版社)， 2011.

[11] SUN Yan-kui(孙延奎). Wavelet Analysis and Applications. Beijing: China Machine Press， 2005.

[12] Yang C, He Z Y, Yu W C. BMC Bioinformatics， 2009. 10.

[13] Zhang Z M, Chen S, Liang Y Z, et al. Journal of Raman Spectroscopy, 2010, 41: 659.

*Corresponding author

Baseline Correction Algorithm for Raman Spectroscopy Based on Non-Uniform B-Spline

FAN Xian-guang, WANG Hai-tao, WANG Xin*, XU Ying-jie, WANG Xiu-fen, QUE Jing

School of Physics and Mechanical & Electrical Engineering, Xiamen University, Xiamen 361005, China

As one of the necessary steps for data processing of Raman spectroscopy, baseline correction is commonly used to eliminate the interference of fluorescence spectra. The traditional baseline correction algorithm based on polynomial fitting is simple and easy to implement, but its flexibility is poor due to the uncertain fitting order. In this paper, instead of using polynomial fitting, non-uniform B-spline is proposed to overcome the shortcomings of the traditional method. Based on the advantages of the traditional algorithm, the node vector of non-uniform B-spline is fixed adaptively using the peak position of the original Raman spectrum, and then the baseline is fitted with the fixed order. In order to verify this algorithm, the Raman spectra of parathion-methyl and colza oil are detected and their baselines are corrected using this algorithm, the result is made comparison with two other baseline correction algorithms. The experimental results show that the effect of baseline correction is improved by using this algorithm with a fixed fitting order and less parameters, and there is no over or under fitting phenomenon. Therefore, non-uniform B-spline is proved to be an effective baseline correction algorithm of Raman spectroscopy.

Raman spectroscopy; Baseline correction; Non-uniform B-spline; Node vector; Peak position

Dec. 23, 2014; accepted Apr. 18, 2015)

2014-12-23，

2015-04-18

国家重大科学仪器设备开发专项(2011YQ03012417)资助

范贤光， 1980年生， 厦门大学物理与机电工程学院机电工程系副教授 e-mail: fanxg@xmu.edu.cn *通讯联系人 e-mail: xinwang@xmu.edu.cn

O657.3

A

10.3964/j.issn.1000-0593(2016)03-0724-05