小波变换基线扣除对激光诱导等离子体温度计算的改善

刘 莉，肖平平

宜春学院物理科学与工程技术学院，江西 宜春 336000

小波变换基线扣除对激光诱导等离子体温度计算的改善

刘 莉，肖平平

宜春学院物理科学与工程技术学院，江西 宜春 336000

温度是激光诱导等离子体特性研究最重要的参数之一，为降低光谱连续背景对Boltzmann平面法计算等离子体温度的精密度的影响，利用小波变换对等离子体光谱进行分解，并采用软阈值法对代表光谱基线的低频信号进行扣除。选择合适的小波分解层数L及阈值系数α能有效提高Boltzmann图的线性相关度，即有更高的拟合系数R2，从而提高等离子体温度的计算精密度。对低合金钢样品417～445 nm波段LIBS光谱采用db4小波函数进行分解、基线扣除和信号重构，选用12条Fe原子谱线建立Boltzmann图，由Boltzmann图拟合直线的斜率计算得到等离子体温度。对L和α系数进行了优化选择，研究发现，采用8层小波分解时Boltzmann图具有较高的R2，而α的选择与时延td有关，td≤4.0 μs时，α=0.3可获得最佳R2值，之后随td的增大，α逐渐减小； 在td≥6.5 μs后，α=0，即光谱低频信号被完全扣除，说明基线对光谱特征谱线的干扰随时延的增加逐渐减弱。基线扣除后各时延的等离子体温度降低约2 000～3 000 K，温度随时延的增加逐渐降低，与等离子体膨胀过程中温度逐渐下降的物理过程相吻合，且变化过程中的波动变小。

等离子体温度； 小波变换； 基线扣除； 激光诱导击穿光谱

引 言

激光诱导击穿光谱(laser-induced breakdown spectroscopy，LIBS)是一种新型的等离子体发射光谱物质成分分析技术[1]，具有制样简单、成本低、能对各种物质进行多元素实时在线检测的独特优势，但由于LIBS受光谱干扰、基体效应、自吸收效应及环境气氛等因素的影响[2]，LIBS技术在定量分析精度和稳定性上与一些成熟的光谱分析技术相比尚存在差距[3-4]。LIBS技术发展的困难在于对激光与物质的相互作用机理及等离子体内部粒子的相互作用特性的深入理解不够，有待建立新的理论分析模型。光谱分布及其强度是等离子体特性的表象，是物质组分及含量的载体，等离子体温度(T)和电子数密度(Ne)是等离子体特性研究的重要参数[5]。Ne的大小可通过光谱谱线Stark展宽得到，T常见的计算方法有双线法和多谱线Boltzmann平面法[6]。双谱线法计算简单但精度差，Boltzmann平面法过程稍复杂但精度较高。谱线强度的波动、光谱干扰及连续背景等因素是影响T计算精度的主要因素，光谱波动主要受激光能量和环境气氛的影响，光谱干扰可通过提高光谱仪分辨率或光谱分峰的方式解决，连续背景对光谱的影响通常采用基线扣除的方法解决。LIBS光谱基线扣除方法有轮廓曲线拟合法[7]、极小点筛选法[8]及小波变换法(wavelet transform，WT)[9-10]等，WT以其低熵、多分辨率去相关及基函数选择灵活等特性成为基线扣除研究的热点，已将WT基线扣除用于定量分析精度的提高[9-10]，但未见基线扣除用于改善等离子体温度计算精密度的报道。通过WT基线扣除的方法来改善等离子体温度的测量有利于对激光等离子体特性的研究。

1 方法原理

1.1 小波变换基线扣除

WT是将任意L2(R)空间函数f(t)以小波基进行展开，Mallat提出的离散小波变换的快速算法为[11]

(1)

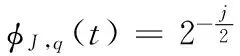
使用小波变换对LIBS光谱进行基线扣除包括小波分解、基线扣除和信号重构三个过程，基线通常被认为是小波分解的低频信息，因此基线扣除一般采用将原始信号中的低频小波系数cJ，q直接置零的方法(硬阈值法)。采用硬阈值法扣除基线，在分解层数较少时经常导致基线过扣除，而分解层数过多则可能导致基线欠扣除，因此我们使用软阈值法，即给低频系数乘一个阈值系数α∈(0，1)，而不是直接置零，可以合理调整基线扣除幅度。软阈值法可表示为

(2)

上述小波变换和基线扣除算法全部基于MATLAB 2011b小波变换工具箱编程实现。

1.2 Boltzmann平面法计算等离子体温度

在满足局部热力学平衡的条件下，各粒子在不同能态的分布服从Boltzmann分布，等离子体发射谱线强度I可表示为[1]

I=(hcN0gA/4πλZ)exp(-E/kT)

(3)

其中，h为Planck常数，c为光速，N0为元素总粒子数密度，g为能级的统计权重，A为跃迁概率，λ为光谱波长，Z为粒子配分函数，E为光谱跃迁上能级，k为Boltzmann常数，T为等离子体温度。将式(3)变形可得到

ln(Iλ/gA)=-E/kT-ln(4πZ/hcN0)

(4)

式(4)是以E为横坐标，以ln(Iλ/gA)为纵坐标的直线方程，其斜率为-1/kT，由此确定的平面称为Boltzmann平面。可见，如果通过实验获得同一元素多条谱线的强度，并结合各谱线对应参数，利用式(4)可建立其Boltzmann散点图，对散点进行直线拟合，由拟合直线的斜率求得等离子体温度。从式(4)可知谱线强度I的实验测量精度是影响等离子体温度计算精度的直接因素，去除光谱基线，消除连续辐射对光谱的影响可改善等离子体温度的计算精度。

2 实验部分

等离子体激发源采用输出波长为1 064 nm的Nd∶YAG激光器，脉冲能量为60 mJ，频率10 Hz，脉冲宽度10 ns。激发样品为低合金钢国家标准样品(GSB03-1525-2000-2)，等离子体光谱通过Czerny-Turner结构光谱仪进行收集，光栅狭缝数1 200 line·mm-1，光谱采集范围417～445 nm，采集不同时延(td=0.5, 1.0, 1.5，…，7.5 μs)的光谱，光谱采集门宽wg=0.5 μs.为增加光谱强度和降低激光能量波动的影响，每个光谱积累六个激光脉冲。

3 结果与讨论

3.1 光谱基线扣除

依据式(3)表示的小波变换基线扣除算法对td=0.5 μs时的光谱进行处理，结果如图1所示。原始光谱由于受复合辐射影响产生强烈的连续背景，背景导致谱线强度非线性增加，采用其谱线计算等离子体温度时产生较大误差。用小波变换扣除光谱基线算法可以降低背景对谱线强度的影响，但采用硬阈值法(α=0)扣除基线会导致基线过扣除，部分连续背景谱线强度出现小于0的情况； 而采用软阈值法(如α=0.3)扣除基线，不仅能有效扣除基线，通过选择适当阈值系数α可以避免基线过扣除。

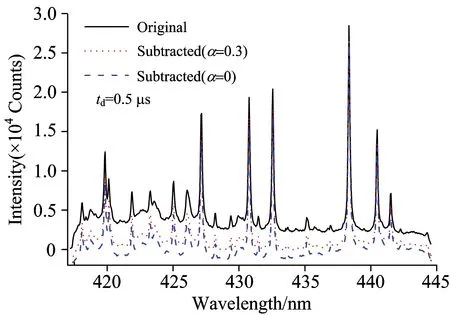
Fig.1 Comparison of the original and its subtracted spectrum

3.2 基线扣除对等的离子体温度计算的改善

从图1所示光谱中选取12条Fe原子谱线用于温度计算，各谱线λ，g，A及E等参数值如表1所示。将各谱线强度和参数代入式(4)可得Boltzmann平面图。图2(a)和(b)为在未采用小波变换基线扣除前td=0.5和2 μs时的Boltzmann平面图。平面中各谱线数据点的线性相关性反映了温度计算的精密度，线性相关性通常用相关系数平方R2表示[11]。图2中，时延为0.5和2 μs时R2分别只有0.59和0.83，较低的R2通常导致较大的温度计算波动和误差。

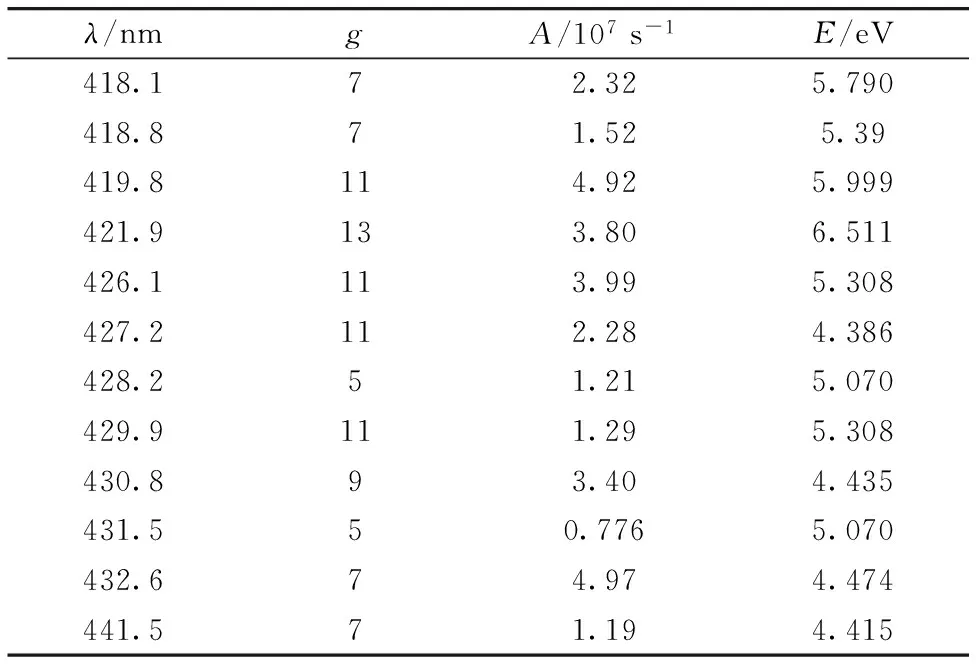
Table 1 Spectroscopic data of selected Fe atomic emission lines

采用小波变换基线扣除算法降低背景信号干扰，有望提高Boltzmann平面测量点的线性拟合系数R2，提高等离子体温度的计算精密度。利用db4小波作为小波变换基函数，首先要选择小波分解层数L，防止基线的过扣除和欠扣除。这里以R2系数最大为标准对小波分解层数L进行优化。图3所示为α=0.3时，不同L对应R2的时延变化图。与无基线扣除的情况相比，在td=0.5 μs且L=5时R2有所降低，这是由于分解层数少而导致基线过扣除造成的; 其他各R2值在扣除基线后都有不同程度的增加。随着分解层数的增加，R2没有明显改善，在td<3 μs有一定提高，但在时延3 μs后却稍有下降。进一步增加分解层数可能导致基线的欠扣除，因此这里选择L=8。除分解层数L外，阈值系数α也需进行优化选择。图4给出了td=0.5，1，2，4，6 μs时基线扣除前及采用不同阈值系数α扣除基线后R2的变化，R2随α的增加先增大后减小，这是由于α较小会导致基线的过扣除，而α较大时导致基线的欠扣除。另外，当td较小时R2最大值对应α较大，td较大时R2最大值对应α较小。从图4还可以看出, 采用硬阈值法(即α=0)扣除基线不能达到最佳效果, 而且在td=0.5 μs时，由于基线严重的过扣除(见图1)而导致R2变差，采用软阈值法对R2都有不同程度的提高。

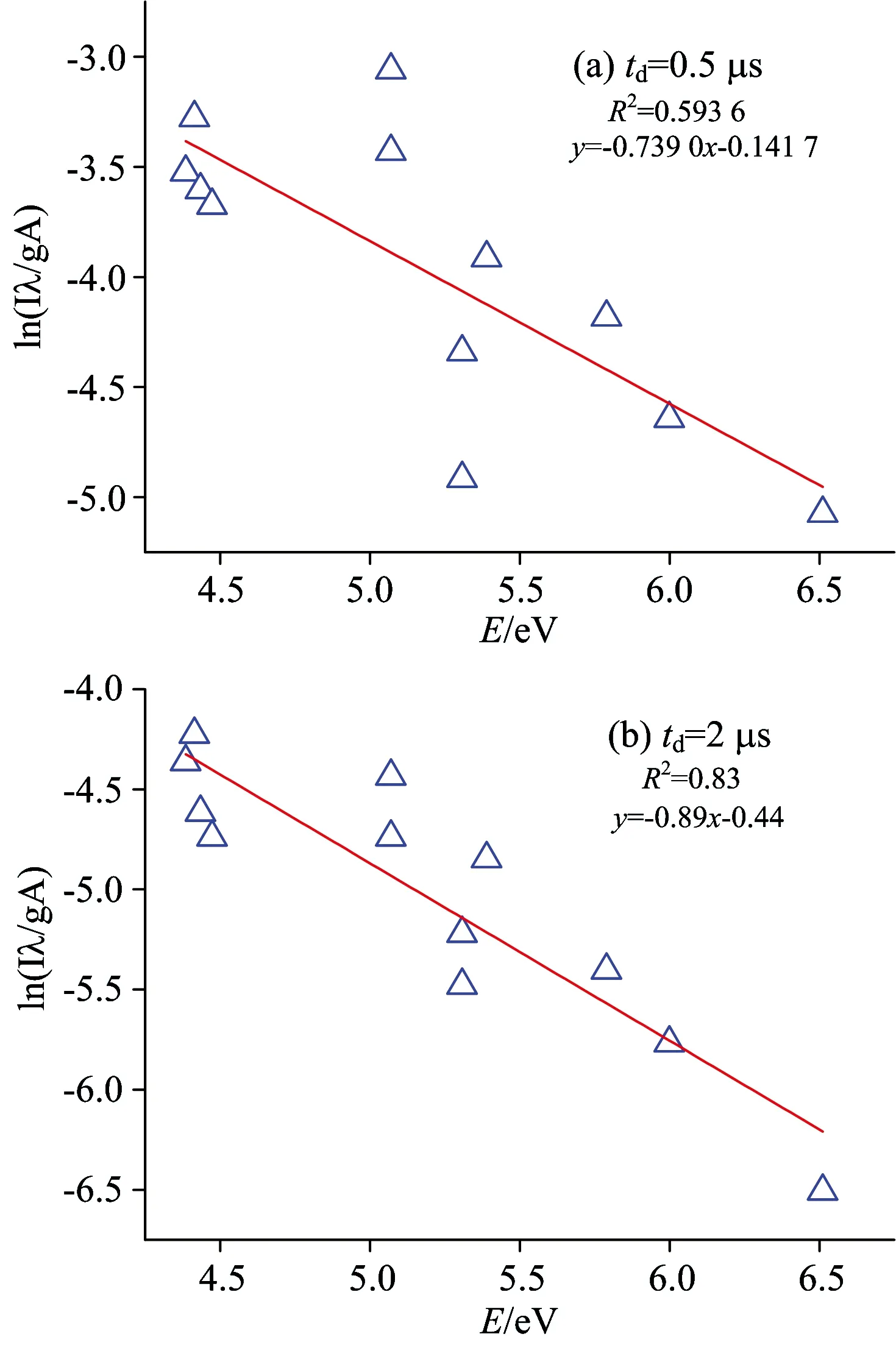
Fig.2 Boltzmann plot without baseline subtraction

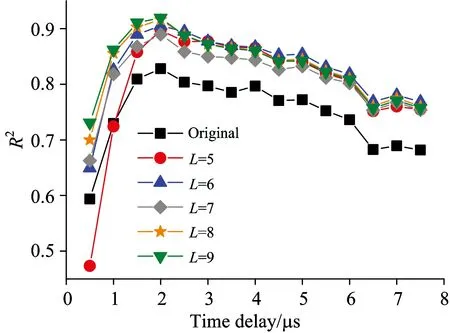
Fig.3 R2 as a function of td for different L

表2给出了不同时延基线扣除前后的R2值及基线扣除最佳阈值系数α，可见，采用小波变换基线扣除算法后R2都得到不同程度的增大。当td≤4.0 μs时，对应α=0.3； 当td=4.5 μs时，α=0.2； 当5.0 μs≤td≤6.0 μs时，α=0.1； 当6.5 μs≤td时，α=0。这是由于等离子体激发初期温度较高，强烈的复合辐射对特征谱线形成强烈干扰，采用较大阈值系数可有效扣除光谱中作为基线的连续背景，因而对R2有较大的改善； 随时延的增加，等离子体逐渐冷却，复合辐射随之减弱，光谱连续背景亦减弱，对谱线的干扰变得无足轻重，即使基线全部扣除也不会造成过扣除而使元素特征谱线信息丢失。

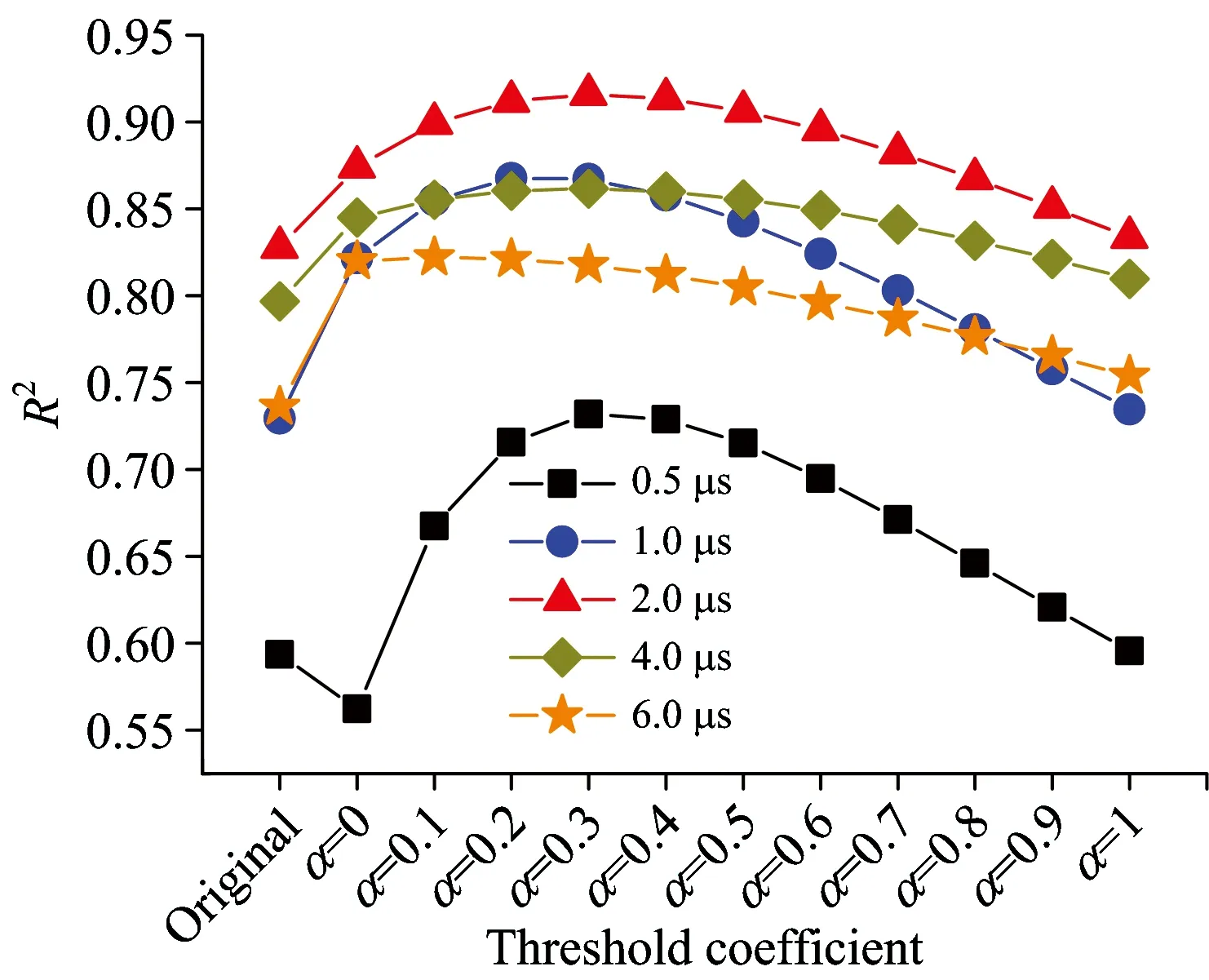
Fig.4 R2 as a function of α for different td

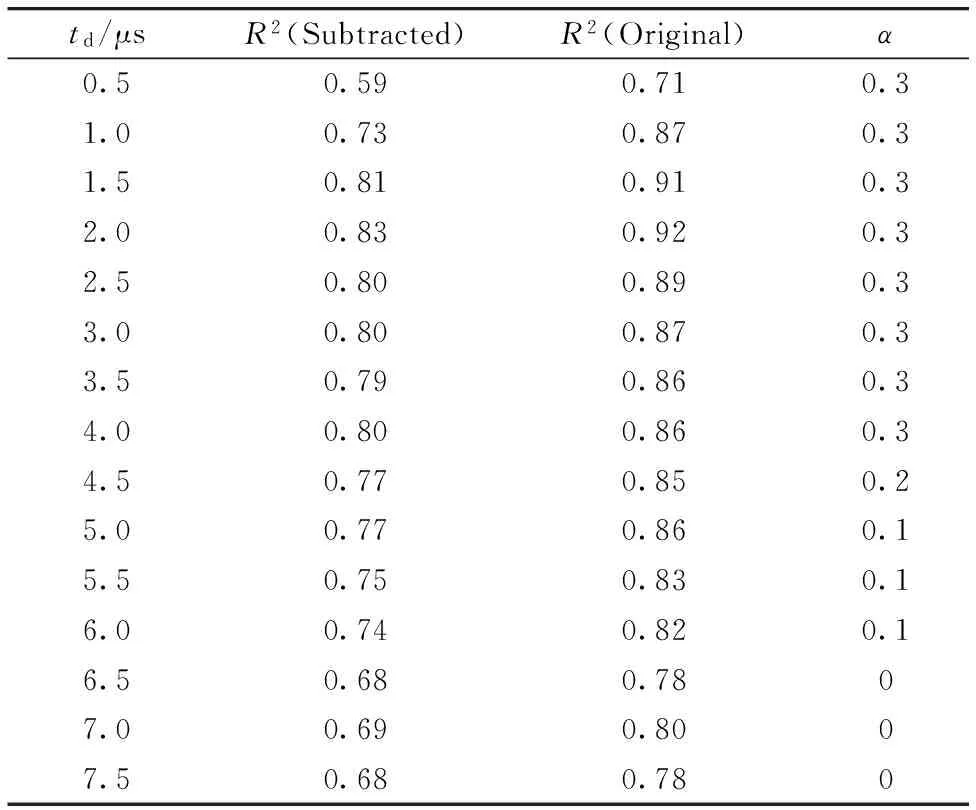
Table 2 R2 and α with and without baseline subtraction

从小波变换基线扣除后的光谱中选择表1中Fe特征谱线建立Boltzmann图，利用拟合直线斜率可以求得基线扣除后的等离子体温度。如图5所示为基线扣除后(a)td=0.5 μs和(b)td=2.0 μs的Boltzmann图，与图2比较可见，基线扣除后拟合直线的R2分别由0.59和0.83增加到0.71和0.92，且斜率分别由-0.74和-0.89减小至-0.90和-1.02，由式(4)可知计算得到的等离子体温度将会降低。基线扣除前后计算得到的等离子体温度随时间的演化对比如图6所示，可见基线扣除前的温度随时延的演化曲线波动较大，且在5 μs后不降反升，不符合等离子体温度变化特性； 在基线扣除之后温度计算值降低约2 000～3 000 K，随时延的增加逐渐减小，与等离子体膨胀过程中温度逐渐下降的物理过程相吻合[12]，而且扣除基线后温度随时延的变化更加平缓。

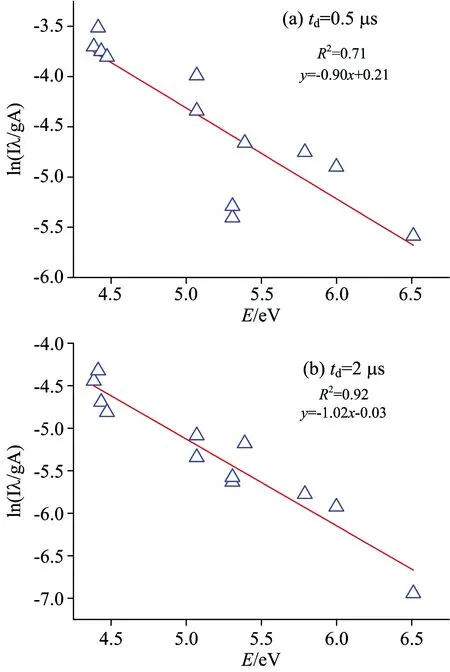
Fig.5 Boltzmann plot with baseline subtraction

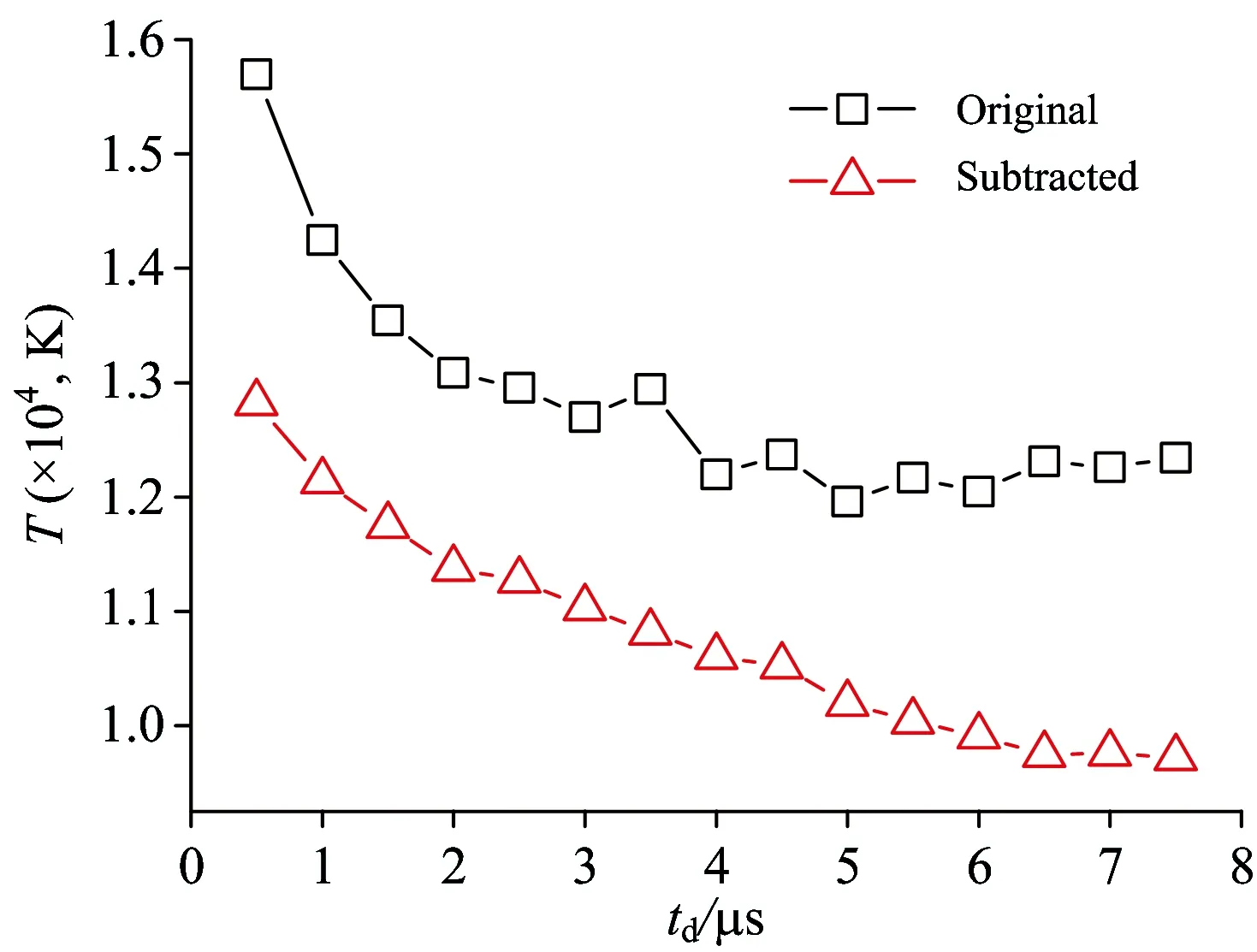
Fig.6 T versus td with and without baseline subtraction

4 结 论

利用小波变换对激光诱导等离子体光谱进行基线扣除，目的在于改善等离子体温度计算的精密度。小波变换基线扣除的硬阈值法会导致过扣除，软阈值法能有效调整基线扣除比例防止基线过扣除，选择合适的小波分解层数L及阈值系数α能有效提高Boltzmann图的线性拟合系数R2，从而提高等离子体温度的计算精度。研究表明，采用db4小波分解8层时能得到较高的R2，而α的选择与时延td有关，td≤4.0 μs时，α=0.3可获得最佳R2值，之后随td的增大，α逐渐减小，在td≥6.5 μs后，α=0，即光谱低频信号被完全扣除，说明基线对光谱特征谱线的干扰随时延的增加逐渐减弱。基线扣除后由Boltzmann图法得到的等离子体温度减小约2 000～3 000 K，且随时延的变化更平滑。激光等离子体温度的精密计算对等离子体与物质相互作用及等离子体的演变特性研究有重要意义。

[1] Singh J P, Thakur S N. Laser-induced Breakdown Spectroscopy. 1st ed. Amsterdam: Elsevier, 2007. 197.

[2] Hahn D W, Omenetto N. Applied Spectroscopy，2010, 64: 335A.

[3] Wang Z, Yuan T B, Hou Z Y, et al. Frontiers of Physics, 2014, 9: 419.

[4] Hahn D W, Omenetto N. Applied Spectroscopy，2012, 66: 347.

[5] Cristoforetti G, Tognoni E, Gizzi L A. Spectrochimica Acta Part B: Atomic Spectroscopy, 2013, 90: 1.

[6] Aguilera J A, Aragon C. Applied Surface Science，2002, 197: 273.

[7] Yaroshchyk P, Eberhardt J E. Spectrochimica Acta Part B: Atomic Spectoscopy, 2014, 99: 138.

[8] Sun L, Yu H. Spectrochimica Acta Part B: Atomic Spectoscopy, 2009, 64: 278.

[9] Yuan T B, Wang Z, Li Z, et al. Analytica Chimica Acta, 2013, 807: 29.

[10] Zou X H, Guo L B, Shen M, et al. Optics Express, 2014, 22: 10233.

[11] XU Lu, SHAO Xue-guang(许 禄, 邵学广). Methods of Chemometrics(化学计量学方法). 2nd ed. Beijing: Science Press(北京： 科学出版社), 2004. 207.

[12] Böker D, Brüggemann D. Spectrochimica Acta Part B: Atomic Spectoscopy, 2011, 66: 28.

Accuracy Improvement of Temperature Calculation of the Laser-Induced Plasma Using Wavelet Transform Baseline Subtraction

LIU Li, XIAO Ping-ping

College of Physics Science and Engineering Technology, Yichun University, Yichun 336000, China

Temperature is one of the most important parameters in studying of laser-induced plasma characteristics. To reduce the impact of continuous background on the calculation of temperatures using Boltzmann plots, the wavelet transform was used to decompose the spectrums, and the low-frequency signals represented the spectral baseline were deducted by using soft-threshold method. Selecting the appropriate wavelet decomposition level L and threshold coefficient α can increase the linear regression coefficient R2 of Boltzmann plots, and the calculation accuracy of plasma temperature was improved. The LIBS spectra of low alloy steel sample region from 417 to 445 nm were decomposed by using db4 wavelet, and then baseline subtraction and signal reconstruction were carried out, respectively. Twelve Fe atomic lines were chosen to establish Boltzmann plots, and the temperatures were calculated from the slope of the fitted lines in the plots. The valueLandαwere optimized accordingR2, the results showed that the 8-layer db4 wavelet decomposition can gain the highR2, while the value ofαassociated with the delay time td, e. g., the optimumαcorresponding to maximum values ofR2is 0.3 whentd≤4.0 μs, and then decrease with the increasing oftd, and reduced to 0 whentd≥6.0 μs. The interference due to baseline on the spectral characteristic lines gradually reduced with the increasing oftd, and thereforeαdecreased withtdincrease. After the baseline was deducted, the temperature calculated by Boltzmann plot decrease of about 2 000 to 3 000 K. The temperature gradually decreased with the increasing of thetd, and the temperature fluctuation is reduced after baseline subtraction, these results are consistent with the physical process of plasma expansion.

Wavelet transforms; Plasma temperature; Baseline subtraction; Laser-induced breakdown spectroscopy

Nov. 16, 2014; accepted Mar. 16, 2015)

2014-11-16，

2015-03-16

国家自然科学基金项目(61168002)，江西省自然科学基金项目(20132BAB201048)和江西省高等学校教学改革研究基金项目(JXJG-14-15-14)资助

刘 莉，1981年生，宜春学院物理科学与工程技术学院讲师 e-mail: ll4246@126.com

O433.4

A

10.3964/j.issn.1000-0593(2016)02-0545-05