通过向量角转换校正拉曼光谱中乘性干扰

姚志湘，孙增强，粟 晖，袁洪福

1. 广西科技大学广西糖资源绿色加工重点实验室，广西 柳州 545006 2. 北京化工大学材料科学与工程学院，北京 100029 3. 广西科技大学生物与化学工程学院，广西 柳州 545006

通过向量角转换校正拉曼光谱中乘性干扰

姚志湘1, 3，孙增强1, 3，粟 晖1, 3，袁洪福2

1. 广西科技大学广西糖资源绿色加工重点实验室，广西 柳州 545006 2. 北京化工大学材料科学与工程学院，北京 100029 3. 广西科技大学生物与化学工程学院，广西 柳州 545006

拉曼光谱强度与物质量存在的线性关系会受到许多复杂因素破坏，包括激发光源、聚焦、散射、折射等，导致定量效果不佳。各种因素的干扰效应，总体上分成加性和乘性效应，而消除乘性效应的难度会更大一些。光谱序列信号可视为向量，信号强度对应向量的模量，而体现向量本质的方向属性不会受模量变化的影响。根据这一原理，利用向量的方向确定性，将信号的强度度量转换成空间角度度量，建立了一种消除乘性效应的方法。首先，选择一个与待定量组分相近而与背景空间近似正交的基准向量，并定义移动窗口； 然后，计算移动窗口内的光谱向量与基准向量的夹角，所得值存储为矩阵，完成角度描述转换。角度矩阵消除了乘性效应的干扰，而定量关系仍然近似线性，只要将该矩阵的秩满足多元统计建模要求，就可以用于多元校正，并得到良好结果。研究采用甲醇-乙醇-异丙醇混合体系，验证了消除乘性效应后改进的定量效果，对于积分时间波动的预测值与实际值，直接PLS方法的相关系数r为0.911 9，预测标准偏差(RMSEP)为0.110 2； 采用MSC预处理的r为0.906 0，RMSEP为0.100 8； 而本文提出的VAPLS的r为0.998 7，RMSEP为0.015 2。结果表明向量角转换度量处理后，光谱的乘性干扰得到了有效校正，拉曼定量分析准确性得到了提高。

拉曼光谱； 乘性效应； 散射校正； 向量角转换

引 言

确定条件下，拉曼散射光强度与组分浓度呈线性关系，此为拉曼光谱定量基础[1]。但是拉曼光谱测量实际存在多种影响定量准确的因素，根据对光谱强度的影响，可分为加性和乘性的。常见的基线漂移、噪声等为加性效应，而光源稳定性、样品的透射和散射、聚焦，积分时间变动，甚至于折射率随液体样品浓度变化等则属于乘性效应，使得拉曼强度与被测组分浓度之间不再是简单的线性关系[2]。常用的乘性校正方法有标准正态变量变换(standard normal variate transformation, SNV)和多元散射校正(也称乘性散射校正，multiplicative scatter correction, MSC)[3]； SNV假设所有变量具有相同的标准偏差，而MSC假设乘性和加性变化远大于样品浓度或化学性质变化[4]，这些假设对于组分性质变化较宽的样品处理效果可能变差，文献表明SNV和MSC处理结果相似[5]。此外，扩展多元散射校正方法(extended MSC, EMSC)需要样品中所有对光谱有贡献的为纯物质光谱，限制了应用[6]，也有文献证明MSC处理后，拉曼光谱反而出现明显的背景倾向[7]。张倩暄等、Chen等[8]对EMSC进行了改进，陈增萍等[10-11]提出了光程长评估与校正算法(optical path length estimation and correction, OPLEC)，进一步又提出了乘性效应模型(multiplicative effects model, MEM)进行散射校正，上述方法可以消除乘性效应，但原理和步骤都比较复杂。

传统上，光谱分析直接关联光谱强度与待测性质，建立光谱强度与预测性质的定量关系。本文提出不将光谱强度与预测性质直接关联，而是转化为向量间的夹角余弦后，再进行多变量计算，以避免针对于强度的乘性干扰，改善定量结果。

1 原理与方法

1.1 原理

确定组成的体系，其光谱与组分浓度间关系表示为

y=Xc+e

(1)

式中，y是测量到的光谱，由体系n个组分纯物质光谱X=[x1,x2, …,xn]，和各组分浓度c=(c1,c2, …,cn)混合贡献而成，同时还叠加了随机误差e。

但是拉曼光谱测量容易受到乘性效应影响，难以严格重复，导致强度不稳定。这些影响归纳到模型中，以乘性因子b，加性因子d代入式(1)

y=bXc+d+e

(2)

式(2)中加性因子d和随机误差e可采用一阶导数平滑和低通滤波、重复平均等方法消除或降低，这些方法原理清晰，可方便地预处理光谱数据[11]。

式(2)的校正关键在于消除乘性因子b，为此引入向量角概念。离散的光谱测量点，可以表达为序列数组，可视为数据空间内的向量[12]。向量模(长度)表示测量强度，而向量方向决定于体系的构成，表达为空间中与确定坐标的夹角[13]。乘性因子b导致强度变化，即改变了向量模，但体系构成未改变，故而向量方向不变，即向量角不随模改变。

如果采用向量角替代向量模描述体系，就能消除乘性因子b。如图1，a和b共同构成向量S，当a和b等比例缩小时，S′与S在方向上不发生改变； 而只有在a与b的比例发生变化时，其共同构成的向量才会发生方向变化，向量角与体系构成比例具有函数关系，该函数与向量模无关。

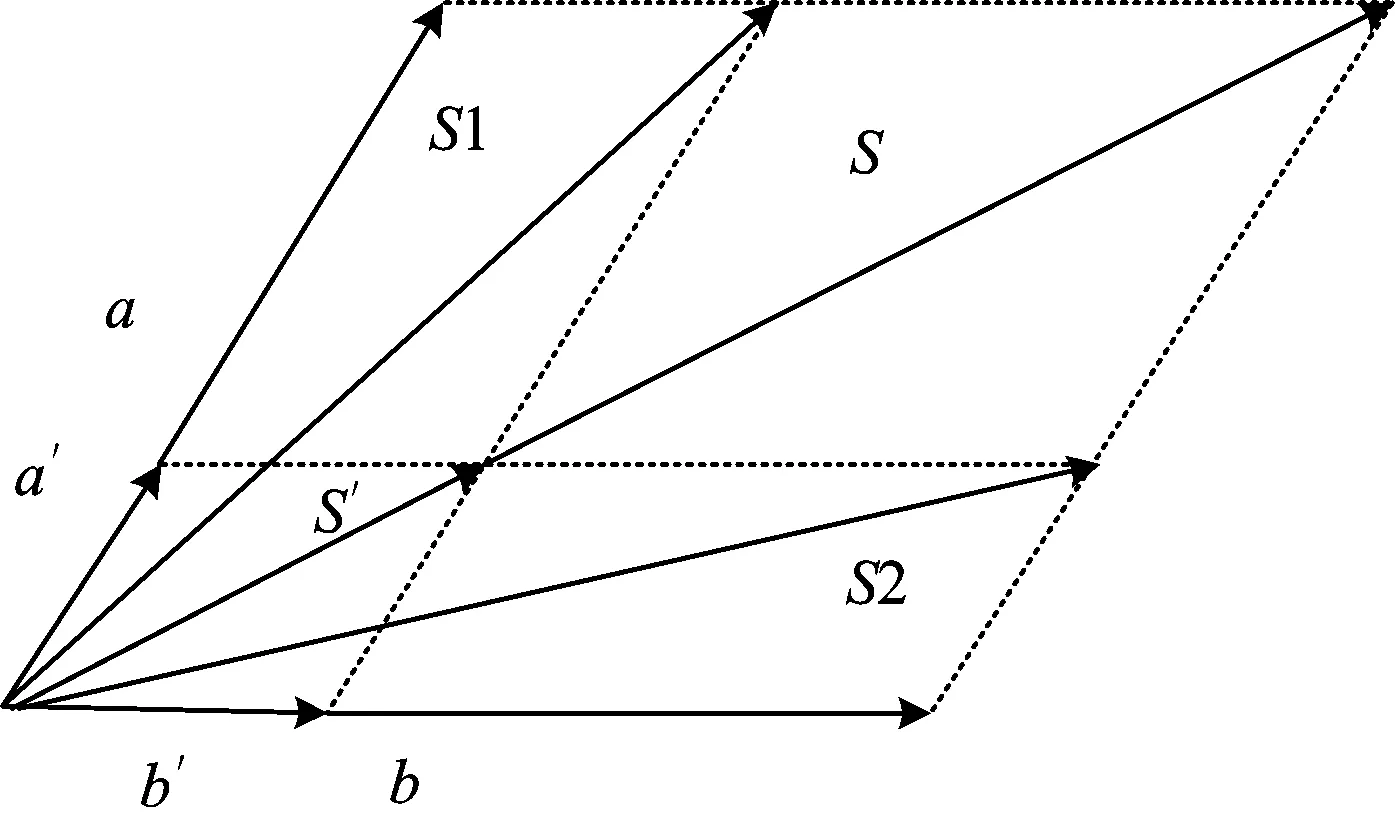
Fig.1 The relationship between system components and vector direction

向量角的描述和计算如图2所示，空间中的固定向量a与随组成变化的向量S存在夹角θ，可用点积式(3)计算

(3)

如果S受到乘性因子b影响变为S′，即

S′=bS

(4)

将式(4)代入式(3)，有

(5)

表明向量角描述不受乘性因子b影响。

进一步，基于向量角描述的定量不能破坏测量值与预测值的基本线性关系。由式(3)和图2可知，S由背景向量d和预测向量f构成，如果将S和d，f的模量归一化，那么S由含量分别为c和cb的f和d构成，即

S=cf+cbd

(6)

(7)

如果参照向量a与背景d呈正交关系，那么有

(8)

Fig.2 The relationship between the analyte contents and vector angle

式(8)中，a，S，f均为单位模量向量，其中a，f是确定向量，因此可以改写成

cosθ=k1c

(9)

而实际情况下，要确定与d完全正交的a比较困难，同时多变量情况下d存在一定幅度的波动。因此，对于选择了近似正交的参照向量a和相对稳定的多变量背景的情况，cosθ可近似保持与c的线性关系，即在一定值域范围内存在如下关系

cosθ≈k1c+k2

(10)

1.2 数据处理方法

根据上述原理，首先选取合适的参比向量a，用于计算量测向量S与其夹角。参比向量应该与背景正交，但与被测组分不正交或相近； 选择被测组分占优分布的空间，进行奇异值分解(SVD)或主成分分解(PCA)，其第一主分量可近似满足这一要求。

然后，将量测信号及参比向量数据划分到若干区间，每个区间为对应的子向量对，计算向量对之间的夹角余弦，形成数组[cos(θ1), cos(θ2), …, cos(θm)]，m为划分的区间数； 多组光谱转化为向量角矩阵Θ=[cos(θi1), cos(θi2), …, cos(θim)]，i=(1,N)，N表示样本个数。相应的组分含量矩阵为Q=[Q1,Q2, …,QN]T，模型近似加和矩阵为R=[R1,R2, …,Rm]，偏差ε。则式(1)和式(2)转为

Θ=QR+ε

(11)

原始量测矩阵向量角转化后，新矩阵的秩不小于体系组分数，即满足多元统计分析的秩要求，就能采用PLS建立多元模型，预测被测组分含量。如果量测存在加性干扰，在执行上述乘性校正处理前，就应该加以去除。

2 实验部分

2.1 仪器和试剂

拉曼光谱仪(QE65000，美国Ocean optics)，激光器(MTS-785-MD600N，美国Mars Electronics)； 光纤探头(BAC100-785-OEM，美国Ocean optics)。

无水乙醇(分析纯)； 甲醇(分析纯)； 异丙醇(分析纯)。

2.2 方法

2.2.1 系列样品配制

准确量取不同体积的乙醇10 mL容量瓶，加入体积各不相同的异丙醇后，以甲醇定容得到乙醇体积分数5%～90%范围的系列样品共30个。

2.2.2 拉曼光谱采集

样品置于光程1 cm石英比色皿，固定拉曼探头与比色皿的间距。以两种方式采集光谱，一是固定积分时间1 s，分别采集30个样品的拉曼光谱； 二是调整积分时间(积分时间范围1～10 s)，采集处于仪器最佳信噪比和线性范围内的光谱。

3 结果与讨论

3.1 数据处理

如图3，选取751～1 600和2 601～3 150 cm-1两段光谱建模，以降低光谱中不含或仅含少量信息的区域对模型的干扰[14]。选择乙醇含量高于80%的4个样本进行SVD分解，将第一分量作为参比向量。将参比向量和样品光谱的300个数据划分到30个子区间，分别计算对应的夹角余弦值，构成尺寸为30×30的矩阵Θ。使用累计方差贡献率确定矩阵Θ的主成分数(化学秩)为3，与体系实际包括甲醇、乙醇、异丙醇3种组分的情况一致，并且矩阵秩满足多元建模要求。

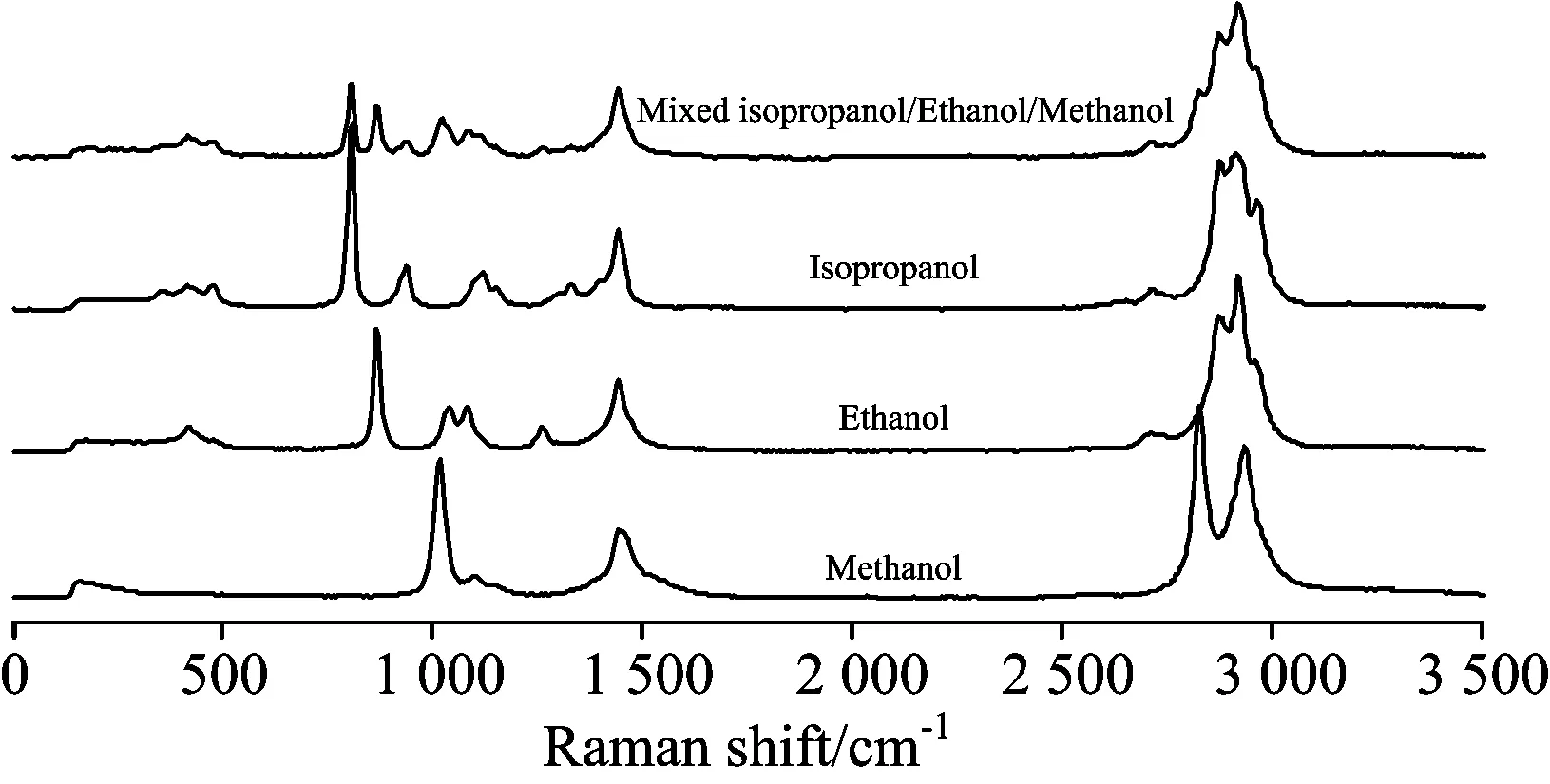
Fig.3 Raman spectra of methanol/ethanol/ isopropyl and their mixture

3.2 定量分析

按照乙醇含量分布，从30组样本中选20组作为校正集，其余作为验证集。固定积分时间1 s，由于测量条件确定，没有显著的乘性效应，采用PLS、向量角+PLS(Vector angle+PLS, VAPLS)的结果如表1和图4所示。

调整样品测量的积分时间，可以使测量结果有较好的信噪比和线性响应，第二种测量方式下，积分时间处于1～10 s不等，因此信号包含了乘性干扰，采用PLS，MSC+PLS和VAPLS分别处理的结果如表2和图5。

表3对比了两种测量方式PLS和经过VAPLS处理后的预测结果，乘性效应显著时，直接PLS结果误差显著，而MSC处理后的PLS，RMSEP略微降低，但预测值与实际值的相关性变差； VAPLS则保持了稳定而理想的定量效果。由于测量信噪比的改善，VAPLS在变动积分时间测量的结果甚至优于固定积分时间测量。

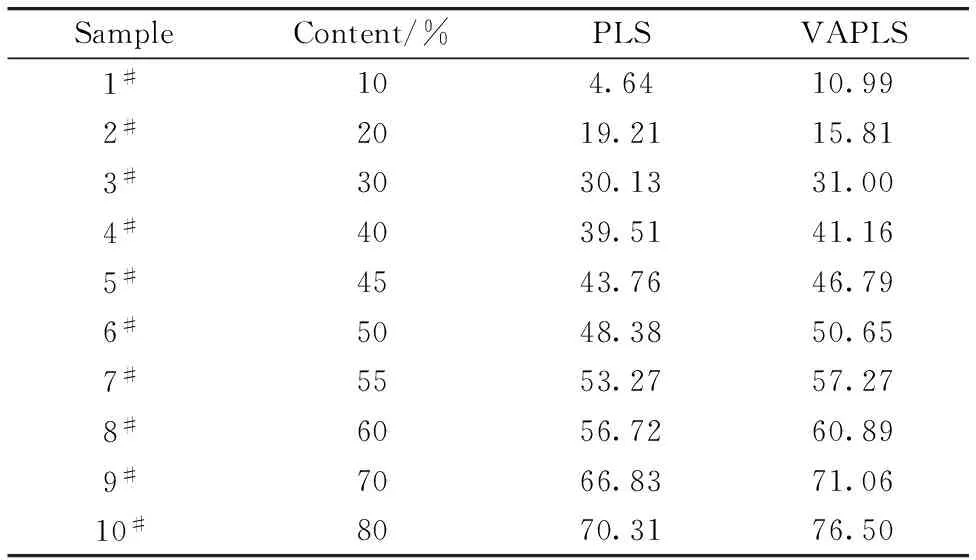
Table 1 Analytical result of ethanol content by different methods at 1S as integration time

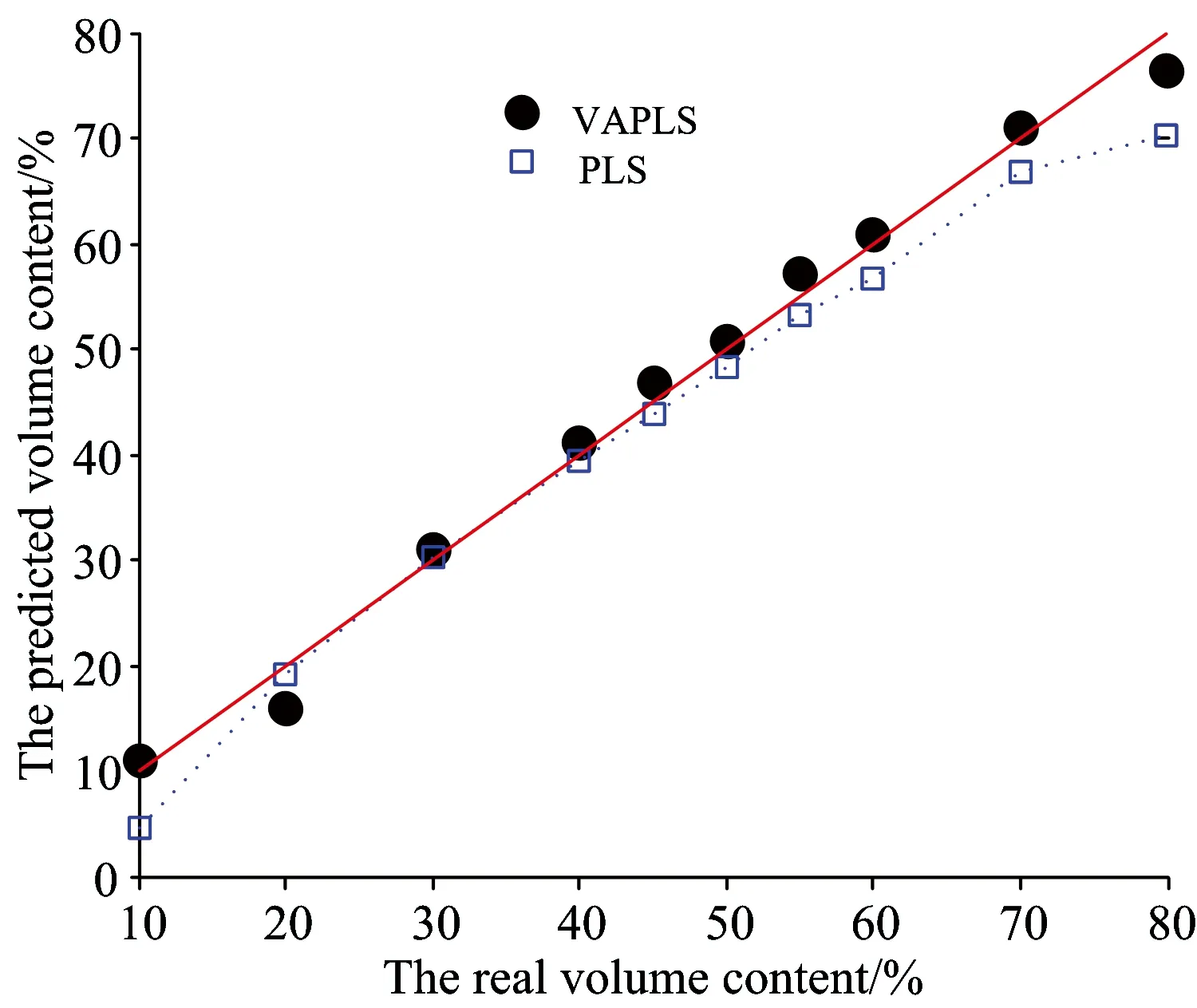
Fig.4 The result of ethanol content by PLS and unvarying integration time (1 s)

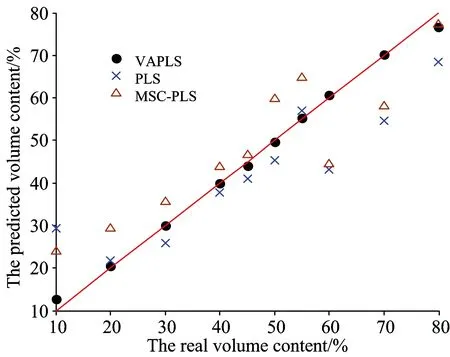
Fig.5 The result of ethanol content by PLS，MSC+PLS VAPLS at an and VAPLS at varying integration time (1 ～10 s)

使用MSC这种经验选取的方法进行乘性效应校正时，参数选择非常重要，如果参数选择不合适或MSC假设不成立，如表2和表3，反而破坏了原始数据间的近似线性关系，导致模型预测能力降低，无法保证校正效果。PLS建模基于测量值与预测值之间的线性关系，未经校正的拉曼光谱，其强度波动降低或破坏了线性关系。拉曼光谱的测量方式无法避免散射和折射的影响，在固定测量条件的预测结果中，可以看出规律性误差，对于高/低含量，误差明显，说明仅仅约束测量条件，无法避免乘性效应误差。

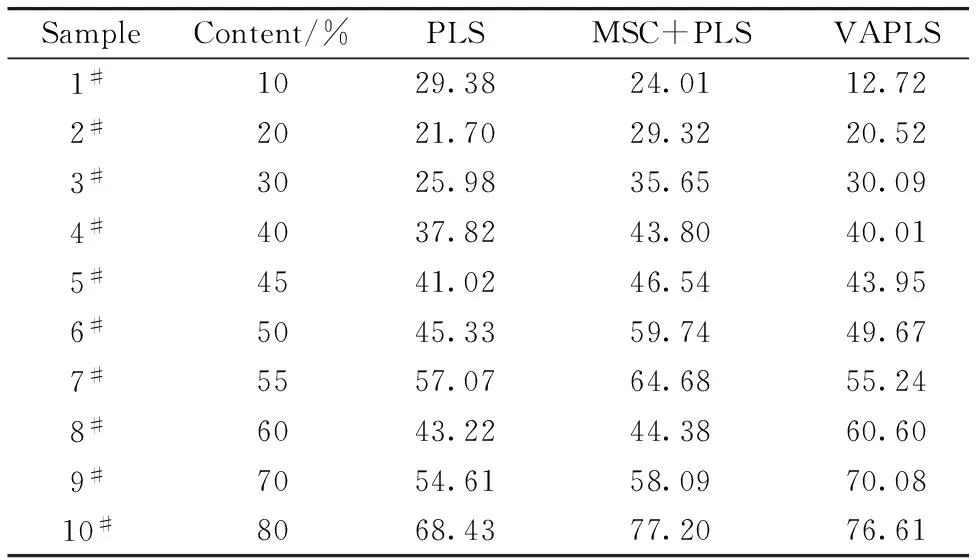
Table 2 Analytical result of ethanol content by different methods at 1～10 s as integration time

Table 3 Analytical result of different methods

通过向量角转换校正乘性效应，利用了向量角不受乘性效应影响的特性，重构线性关系，虽然不是完全严格，但从实验结果可以看出，其损失的准确性通过消除乘性效应得到弥补，因调整参数改善的信噪比和仪器线性响应，又进一步提高了预测精度。

4 结 论

拉曼光谱定量一直受到散射和折射影响，现有方法或效果有限或通常比较复杂。VAPLS方法将光谱数据视为向量，通过向量角转换消除因散射和折射引起的乘性干扰，满足多元分析所需的线性条件。实验结果表明有效改善了定量效果，原理简单、易于理解，数据处理过程便于模块化，对于过程分析和在线监测等难以保证可重复分析条件的应用场合，将具有广泛的应用价值。

[1] HU Jun, HU Ji-ming(胡 军, 胡继明). Chinese Journal of Analytical Chemistry(分析化学), 2000, 28(6): 764.

[2] WANG Shu-xia, LI Li-mei, ZHONG Li-jing, et al(王淑霞, 李丽梅, 仲利静, 等). Journal of Analytical Science(分析科学学报), 2011, 27(6): 782.

[3] Bakeev K D. Process Analytical Technology. 2nd ed. NJ: A John Wiley & Sons, Ltd. 2010. 372.

[4] CHU Xiao-li(褚小立). Molecular Spectroscopy Analytical Technology Combined with Chemometrics and Its Applications(化学计量学方法与分子光谱分析技术). Beijing: Chemical Industry Press(北京: 化学工业出版社), 2011. 48.

[5] Blanco M, Coello J, Montoliu I, et al. Analytica Chimica Acta, 2001, 434: 126.

[6] Jin Jingwei, Chen Zengping, Li Limei, et al. Analytical Chemistry, 2012, 84, 321.

[7] Iversen J A, Berg R W, Ahring B K. Anal. Bioanal. Chem., 2014, 406: 4915.

[8] Chen Y C, Thennadil S N. Analytica Chimica Acta, 2012, 746: 38.

[9] Yang Jing, Chen Zeng Ping, Zhang Juan, et al. Chemometrics and Intelligent Laboratory System, 2013, 126: 6.

[10] Song Mi, Chen Zeng Ping, Chen Yao, et al. Talanta, 2014, 125: 348.

[11] HU Ai-qin, YUAN Hong-fu, SONG Chun-feng, et al(胡爱琴, 袁洪福, 宋春风. 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2014, 34(10): 2606.

[12] YAO Zhi-xiang，SU Hui(姚志湘, 粟 晖). CN102306236A.2012-01-04.

[13] Bai T J, Bai A A. Acta Ecologica Sinica, 2002, 22(6): 950.

[14] CHU Xiao-li, YUAN Hong- fu, LU Wan-zhen(褚小立, 袁洪福, 陆婉珍). Progress in Chemistry(化学进展), 2004, 16(4): 535.

Correction Multiplicative Effects in Raman Spectra through Vector Angle Transformation

YAO Zhi-xiang1，3, SUN Zeng-qiang1, 3, SU Hui1, 3, YUAN Hong-fu2

1. Guangxi Key Laboratory of Sugar Resources Green Processing，Guangxi University of Science and Technology，Liuzhou 545006, China 2. College of Materials Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China 3. College of Biological and Chemical Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China

The linear relationship between the Raman spectral intensity and the analyte amount is frequently disrupted for a variety of complex reasons, which include these variations in laser source, focusing effect, sample scattering and refracting, so that causes poor quantitative results. As a whole, these disturbing effects can be divided to be additive and multiplicative, and the multiplicative effects are generally more difficult to be eliminated. A spectrum is a series data, also can be treated as a vector. In principle, unstable motions in spectrum intensity/amplitude corresponding to the module shifts for a vector, doesn’t impact the vector direction which is the essence of the vector, so it is reasonable to rewrite the data form on module to on space angle for the same measurement. This thesis employed a data transformation to eliminate the multiplicative effects within spectra, i. e., the spectrum signal on its amplitude has been transformed to be on the vector angles. The first step of the transformation is the selection of a stand vector which is near to the analyte and almost orthogonal to the background within the sample space; and the next step is to define a moving window, then to find out the angle between the sample vector (i. e. the transformed spectrum) and the stand vector within the window; while the window is moved along the spectrum data series, the transformation for vector angle (VA) series has been finished. The thesis has proved that an approximate linear quantitative relationship has been remained in the VA series. Multivariate calibration need full rank matrix which is combined by spectrum from variety samples, and variety VA series also can combine a full rank VA matrix, so the approximate linear VA matrix still perfectly meeting the demand for multivariate calibration. A mixed system consisted by methanol-ethanol-isopropanol has been employed to verify the eliminations to the multiplicative effects. These measuring values of the system are obtained at different Raman integral times and have remarkable multiplicative effects. In predicting results, the correlation coefficient (r) and the root mean squared error of prediction (RMSEP) from class PLS respectively are 0.911 9 and 0.110 2, and 0.906 0 and 0.100 8 are for the preprocessing by multiplicative scatter correction (MSC). In contrast,rand RMSEP under the VAPLS, presented by this thesis, respectively are 0.998 7 and 0.015 2 and are significantly better than others. The VAPLS has eliminated the multiplicative effects of Raman spectra and improved the accuracy of Raman quantitative analysis and it owes to the preprocessing of the vector angle transformation.

Raman spectrum; Multiplicative effects; Scatter correction; Vector angle transformation

Oct. 13, 2014; accepted Feb. 4, 2015)

2014-10-13，

2015-02-04

国家科技支撑计划课题(2011BAE11B00), 广西自然科学基金项目(2014GXNSFAA118056)，广西科技计划项目(桂科攻 1355010-15)资助

姚志湘，1968 年生，广西科技大学广西糖资源绿色加工重点实验室教授 e-mail: zxyao@21cn.com

O657.37

A

10.3964/j.issn.1000-0593(2016)02-0419-05