一种基于Map/Reduce分布式计算的恒星光谱分类方法

潘景昌， 王 杰， 姜 斌， 罗阿理, ， 韦 鹏， 郑 强

1. 山东大学(威海)机电与信息工程学院， 山东 威海 264209

2. 中国科学院光学天文重点实验室， 国家天文台， 北京 100012

3. 烟台大学计算机与控制工程学院， 山东 烟台 264005

一种基于Map/Reduce分布式计算的恒星光谱分类方法

潘景昌1， 王 杰1， 姜 斌1， 罗阿理1, 2， 韦 鹏2， 郑 强3

1. 山东大学(威海)机电与信息工程学院， 山东 威海 264209

2. 中国科学院光学天文重点实验室， 国家天文台， 北京 100012

3. 烟台大学计算机与控制工程学院， 山东 烟台 264005

天体光谱中蕴含着非常丰富的天体物理信息， 通过对光谱的分析， 可以得到天体的物理信息、 化学成分以及天体的大气参数等。 随着LAMOST和SDSS等大规模巡天望远镜的实施， 将会产生海量的光谱数据， 尤其是LAMOST正式运行后， 每个观测夜产生大约2～4万条光谱数据。 如此海量的光谱数据对光谱的快速有效的处理提出了更高的要求。 恒星光谱的自动分类是光谱处理的一项基本内容， 该研究主要工作就是研究海量恒星光谱的自动分类技术。 Lick线指数是在天体光谱上定义的一组用以描述光谱中谱线强度的标准指数， 代表光谱的物理特性， 以每个线指数最突出的吸收线命名， 是一个相对较宽的光谱特征。 研究了基于Lick线指数的贝叶斯光谱分类方法， 对F， G， K三类恒星进行分类。 首先， 计算各类光谱的Lick线指数作为特征向量， 然后利用贝叶斯分类算法对三类恒星进行分类。 针对海量光谱的情况， 基于Hadoop平台实现了Lick线指数的计算， 以及利用贝叶斯决策进行光谱分类的方法。 利用Hadoop HDFS高吞吐率和高容错性的特点， 结合Hadoop MapReduce编程模型的并行优势， 提高了对大规模光谱数据的分析和处理效率。 该研究的创新点为： (1) 以Lick线指数作为特征， 基于贝叶斯算法实现恒星光谱分类； (2) 基于Hadoop MapReduce分布式计算框架实现Lick线指数的并行计算以及贝叶斯分类过程的并行化。

Lick线指数； 恒星光谱分类； Hadoop

引 言

当代天文学的研究极大程度上依赖对天体目标的观测， 如今， 随着科学技术的快速发展， 对天体的观测能力也大大提高， 产生了一系列大规模光谱巡天项目， 如斯隆数字巡天(SDSS)[1-2]， LAMOST[3-4]等。 这些巡天项目产生的海量光谱数据对光谱的自动化处理提出了更高的要求， 其中， 恒星光谱的自动化分类是光谱分析的一项重要内容。 利用恒星光谱的流量信息对光谱进行分类的方法比较多， 包括基于SVM的光谱分类[5]， 基于人工神经网络ANN的光谱分类[6]等。

在综合分析研究已有方法的基础上， 本文提出一种利用线指数特征进行恒星光谱分类的方法； 同时考虑到海量光谱的情况， 基于Hadoop Map/Reduce分布式计算框架实现了线指数的计算以及基于贝叶斯决策的恒星光谱分类方法。 利用Hadoop HDFS高吞吐率和高容错性的特点， 结合Hadoop Map/Reduce编程模型的并行优势， 极大地提高了大规模恒星光谱数据的分析和处理效率， 同时也表明了先进的计算架构和技术， 对于提高科学研究的效率具有很重要的意义。

1 线指数

线指数是指在天体光谱上定义的一组用以描述光谱中谱线强度的标准指数。 本文中采用了目前较为流行和广泛使用的Lick线指数。 该套线指数在恒星光谱的4 000～6 500 Å波段范围内定义了25个突出的吸收特征， 包括19条原子吸收线指数和6条分子吸收线指数， 是相对较宽的光谱特征。 该系统定义中包括光谱吸收谱线的中心波长以及两侧的蓝、 红两端连续谱波段的起止波长。 每条线指数包含了大量的不同元素的吸收特征， 并以该线指数所在波段内最突出的吸收线来命名[7-9]。 有关Lick线指数的完整定义参见Worthey的网站http://astro.wsu.edu/worthey/html/system.html。

Lick线指数的计算方式有两种， 其中19条原子吸收线指数是以等值宽度的方式计算

(1)

另外6条分子吸收线指数以星等的形式计算

(2)

其中，λ1和λ2分别为中心波段起止波长，FIλ和FCλ分别表示在中心波段的单位波长的光谱流量与伪连续谱的流量。

2 基于Hadoop的Lick线指数计算

Hadoop是一个专门针对海量数据设计的分布式软件框架， 利用其两大核心组件HDFS分布式文件系统和MapReduce计算模型可以高效地处理和分析海量数据， 其中， HDFS提供对文件的分布式存储和访问等操作， 在此基础上， MapReduce实现计算任务的分割、 执行、 结果合并等。

Hadoop集群的结构是由一个管理节点和若干工作节点组成的主从结构， HDFS和MapReduce也是典型的主从结构。 HDFS是由一个NameNode(名称节点)和若干DataNode(数据节点)组成， NameNode负责记录和管理DataNode上存储的数据。 类似于HDFS的主从结构， MapReduce中也有对应的JobTracker(作业跟踪器)和TaskTracker(任务跟踪器)， 其中， JobTracker负责将用户需要执行的作业拆分后分散到各个工作节点上， TaskTracker则负责接收分配过来的任务， 并实时地向JobTracker汇报该节点上任务的运行情况。

本文提出的方法基于HDFS和MapReduce的原理实现了对于Lick线指数计算的并行化， 极大提高了对大规模光谱的处理效率。

实验使用的数据是SDSS发布的DR8光谱数据， 从中选取信噪比(signal to noise ratio， SNR)大于20的F， G， K型星， 去掉流量为NULL的数据后共284875条光谱数据。

Hadoop适用于处理单个的大数据文件， 对于大量小文件的情况， 会严重影响Hadoop的扩展性和性能。 所谓小文件是指文件的大小远远小于HDFS上block(默认块大小为64 MB)大小的文件。 首先， 在HDFS中， 所有的block， 文件以及索引目录都以对象的形式存放在NameNode(名称节点)的内存中， 每个对象约占150字节。 对于海量的小文件， 每个文件都要占用一个block， 则需要占用NameNode大量的内存空间。 其次， 访问大量小文件的效率远远小于访问大文件， 因为需要不断的从一个DataNode(数据节点)到另一个DataNode来读取文件， 会大大降低访问的效率。 另外， MapReduce处理大量小文件的效率也要比处理相同大小的大文件的效率低很多， 因为针对每一个小文件就要启动一个task， 而启动task会耗费很多时间， 这样就造成启动和释放task耗费的时间远大于处理文件本身所需要的时间。

实验中用到的FITS文件有将近20万个， 每个只有170 kB左右。 在Hadoop平台上直接对这些小文件处理会严重影响性能， 因此需要对这些FITS文件进行预处理。 预处理的过程是从每个FITS文件中读取出波长和流量信息， 存放在同一个文本文件中。

对每条光谱计算Lick线指数的过程是独立的， 因此可以通过将大样本数据分割后分布到多个节点上计算实现Lick线指数计算过程的并行化。 具体步骤如下：

(1) 将输入数据上传到HDFS上。

输入数据是经过预处理后存放在文本文件中的光谱数据， 每一行代表一条光谱的信息， 包括PLATE-MJD-FIBERID， 波长， 流量。 输入数据存放在HDFS上时会被分割成固定大小的数据块。

(2) Map阶段。

Hadoop将HDFS上的一个数据块作为一个输入分片， 并为每个输入分片创建一个Map Task， 对于输入分片中的每条记录依次调用Map函数进行处理。 本实验中Map函数的任务是根据每条光谱的波长和流量计算其对应的Lick线指数， 输出为每条光谱对应的Lick线指数。

(3) 将计算结果汇总后写入HDFS。

Map阶段结束后， Hadoop会调用默认的Reduce函数， 将Map函数的输出汇总后写入HDFS中。

本文以284 875条光谱数据作为输入数据， 分别在单机上和由一个主节点和8个从节点构成的集群上运行， 运行时间的对比结果如表1所示。 可以看出， 在集群上计算Lick线指数效率比在单机上有明显提高。

表1 单机模式与Hadoop集群模式运行时间比较

3 Hadoop平台下基于贝叶斯算法的光谱分类

在分类问题中， 利用贝叶斯公式， 以分类错误最小为目标的决策方法称为基于最小错误率的贝叶斯决策。 假设分类样本有d种特征值x1,x2, …,xd， 则称x=[x1,x2, …,xd]T为d维特征向量。 分类样本的类别个数为c， 以w1,w2, …,wc表示各个类别， 每个类别wi对应的先验概率为P(wi)， 类条件概率密度为p(x|wi)，P(x)为训练数据x的先验概率。 利用贝叶斯公式可以得到每个类别对应的后验概率P(wi|x)

(3)

基于最小错误率的贝叶斯决策的规则是： 如果P(wi|x)=maxP(wj|x)，j=1, …,c， 则把x归为wi类。 由于样本的先验概率P(x)是独立于wi的常量， 在很多实际应用中， 计算类别的后验概率P(wi|x)时常常忽略P(x)。 因此基于最小错误率的贝叶斯决策的规则又可以描述为： 如果p(x|wi)P(wi)=max{p(x|wj)P(wj)}，j=1, …,c， 则x属于类别wi。 在实际分类工作中， 总体的先验概率P(wi)和类条件概率密度p(x|wi)往往是未知的， 因此需要从收集的有限数量的样本中估计P(wi)和p(x|wi)。

本文首先计算恒星光谱的Lick线指数作为特征向量x， 然后利用基于最小错误率的贝叶斯决策进行分类， 将恒星光谱分为F， G， K三类， 分别以w1,w2,w3表示。 各个类别对应的先验概率P(wi)通过计算训练样本中每个类的比例来估计， 类条件概率密度p(x|wi)则通过Parzen窗法来估计

(4)

其中，x是待分类的样本， 即测试样本，xi是属于类别wi的训练样本，n是训练样本中属于wi类的样本个数，h为窗宽，K为核函数。

使用Parzen窗法对类条件概率密度进行估计时， 窗宽和核函数的选择会对估计效果有影响。 由于高斯核函数(又称为正态分布函数)具有连续性， 利用Parzen窗法计算概率密度函数时是通过对高斯核函数的加和得到的， 因此计算出来的概率密度函数也具有连续性， 相应的概率密度曲线也更光滑， 因此本文选择高斯核函数作为核函数

(5)

本节使用的实验数据是由SDSS发布的DR8恒星光谱数据， 选取F， G， K三种星型的光谱数据。 其中， 取信噪比为100的4660条光谱数据作为训练样本， 信噪比大于20的284 875条光谱数据作为测试样本。 根据第2节介绍的方法分别计算出训练样本和测试样本的Lick线指数作为本次实验的输入数据。

实验的目标是基于MapReduce计算模型实现贝叶斯分类， 由于对每个测试样本进行贝叶斯分类的过程是独立的计算过程， 与其他测试样本不存在计算顺序上的相关性， 根据HDFS和MapReduce计算模型的分布式原理， 可以将测试样本分割后分布在多个节点上进行贝叶斯决策的计算过程。 测试样本数据存放在HDFS上时会被分割成固定大小的数据块， 默认为64MB。 默认情况下， MapReduce将一个数据块作为一个输入分片， 并为每一个输入分片创建一个Map Task实现分布式计算。 本次实验所用的数据所占的存储空间较小， 只有135.5 MB， 但实际的样本个数很大， 使用默认的输入分片并行效果并不明显， 因此， 为了达到更好的并行效果， 实验将输入分片设置为5 MB。 实验的具体步骤如下：

(1) 将输入数据上传到HDFS上。

输入数据是存放在文本文件中的Lick线指数， 每一行代表一条光谱的信息， 包括PLATE-MJD-FIBERID， Lick线指数， 光谱类别。

(2) Map阶段。

该阶段会对输入分片中的每一条测试数据依次调用Map函数进行处理， Map函数的任务是读取训练数据集， 然后对每个测试样本数据计算其对应的各个类别的后验概率， 并将后验概率最大值所对应的类别作为该测试样本数据所属的类别。 Map阶段的输出是每一条光谱的唯一标识PLATE-MJD-FIBERID以及通过贝叶斯决策得到的光谱类别。

(3) 将计算结果汇总后写入HDFS。

调用Hadoop默认的Reduce函数， 将Map函数的输出汇总后直接写入HDFS中。

实验对284 875条光谱数据进行贝叶斯分类， 分别在单机上和由一个主节点和8个从节点构成的集群上运行， 得到的分类结果相同， 分类正确率约为84.4%(240 381/284 875)， 运行时间的对比结果如表2所示。 可以看出， 在集群上进行贝叶斯分类效率比在单机上有明显提高。

表2 单机模式与Hadoop集群模式运行时间比较

使用Parzen窗法对类条件概率密度进行估计时， 窗宽不同会对估计效果有影响。 本文在[0.1, 2.0]范围内， 以0.1为步长， 对不同的窗宽进行了分类实验， 得到的分类正确率如图1所示。

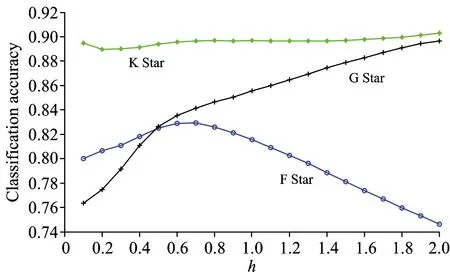
图1 三种类型光谱在不同核窗宽度下的

Fig.1 Bayesian classification accuracy of three type spectra with different kernel width

从图中可以看出， K类恒星的分类正确率受窗宽的影响不大， 而F和G类恒星对窗宽的变化比较敏感。 随着窗宽的增加， G类恒星的分类正确率逐渐提高。 窗宽从0.1增加到0.7时， F类恒星的分类正确率逐渐提高， 但在0.7～2.0区间内， F类恒星的分类正确率随之降低。

4 结 论

对于海量光谱的情况， 利用分布式平台实现光谱的自动化分类是非常重要的一项工作。 本文研究了基于Lick线指数， 利用贝叶斯算法对光谱进行分类的方法， 并在Hadoop平台下实现了Lick线指数的计算以及贝叶斯分类算法。 实验取得的分类正确率为84.4%， 8节点集群运行时间约为单机模式下的6%。 这说明在Hadoop平台下可以明显提高对海量光谱数据的分析和处理效率。 另外， 在利用贝叶斯进行分类时， 需要利用Parzen窗方法计算类条件概率密度， 而Parzen窗方法中不同的窗宽取值会影响最终分类效果， 通过实验研究了不同窗宽对各类恒星分类效果的影响， 实验证明， K类恒星的分类正确率受窗宽的影响不大， 而F和G类恒星对窗宽的变化比较敏感。

在Hadoop环境下实现了贝叶斯决策方法的并行化并应用于光谱的自动分类， 取得了较好的效果， 后续工作中还可以实现其他算法的并行化， 应用于光谱数据的自动分类及参数测量， 进一步提高海量光谱数据的分析和处理效率。

[1] Sloan Digital Sky Survey: http://www.sdss.org/.

[2] Jianmin Si, et al. Science China-Physics Mechanics & Astronomy, 2014, 57(1): 176.

[3] LAMOST Experiment for Galactic Understanding and Exploration(LEGUE)—The Survey’s Science Plan. Research in Astronomy and Astrophysics, 2012, 12(7): 735.

[4] Cui X, et al. Research in Astronomy and Astrophysics, 2012, 12(9): 1197.

[5] Bu Yude, Chen Fuqiang, Pan Jingchang. New Astronomy, 2014, 28: 35.

[6] Navarro S G, Corradi R L M, Mampaso A. Astronomy & Astrophysics, 2012, 538.

[7] Daniel Thomas, Claudia Maraston, Jonas Johansson. Monthly Notices of the Royal Astronomical Society, 2011, 412(4): 2183.

[8] Jonas Johansson, Daniel Thomas, Claudia Maraston. Monthly Notices of the Royal Astronomical Society, 2010, 406(1): 165.

[9] Franchini M, et al. Astrophysical Journal, 2011, 730(2): 117.

A Method of Stellar Spectral Classification Based on Map/Reduce Distributed Computing

PAN Jing-chang1, WANG Jie1, JIANG Bin1, LUO A-li1, 2, WEI Peng2, ZHENG Qiang3

1. School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Weihai 264209, China

2. Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China

3. College of Computer and Control Engineering, Yantai University, Yantai 264005, China

Celestial spectrum contains a great deal of astrophysical information. Through the analysis of spectra, people can get the physical information of celestial bodies, as well as their chemical composition and atmospheric parameters. With the implementation of LAMOST, SDSS telescopes and other large-scale surveys, massive spectral data will be produced, especially along with the formal operation of LAMOST, 2 000 to 4 000 spectral data will be generated each observation night. It requires more efficient processing technology to cope with such massive spectra. Automatic classification of stellar spectra is a basic content of spectral processing. The main purpose of this paper is to research the automatic classification of massive stellar spectra. The Lick index is a set of standard indices defined in astronomical spectra to describe the spectral intensity of spectral lines, which represent the physical characteristics of spectra. Lick index is a relatively wide spectral characteristics, each line index is named after the most prominent absorption line. In this paper, the Bayesian method is used to classify stellar spectra based on Lick line index, which divides stellar spectra to three subtypes: F, G, K. First of all, Lick line index of spectra is calculated as the characteristic vector of spectra, and then Bayesian method is used to classify these spectra. For massive spectra, the computation of Lick indices and the spectral classification using Bayesian decision method are implemented on Hadoop. With use of the high throughput and good fault tolerance of HDFS, combined with the advantages of MapReduce parallel programming model, the efficiency of analysis and processing for massive spectral data have been improved significantly. The main innovative contributions of this thesis are as follows. (1) Using Lick indices as the characteristic to classify stellar spectra based on Bayesian decision method. (2) Implementing parallel computation of Lick indices and parallel classification of stellar spectra using Bayesian based on Hadoop MapReduce distributed computing framework.

Lick line index； Stellar spectral classification； Hadoop

Mar. 2, 2015; accepted Aug. 15, 2015)

2015-03-02，

2015-08-15

国家自然科学基金项目(U1431102， 11473019)资助

潘景昌， 1963年生， 山东大学(威海)机电与信息工程学院教授 e-mail: pjc@sdu.edu.cn

P145.4

A

10.3964/j.issn.1000-0593(2016)08-2651-04