基于线指数特征的海量恒星光谱聚类分析研究
2016-06-15王光沛潘景昌衣振萍
王光沛, 潘景昌*, 衣振萍, 韦 鹏, 姜 斌
1. 山东大学(威海)机电与信息工程学院, 山东 威海 264209
2. 中国科学院光学天文重点实验室, 国家天文台, 北京 100012
基于线指数特征的海量恒星光谱聚类分析研究
王光沛1, 潘景昌1*, 衣振萍1, 韦 鹏2, 姜 斌1
1. 山东大学(威海)机电与信息工程学院, 山东 威海 264209
2. 中国科学院光学天文重点实验室, 国家天文台, 北京 100012
聚类分析是数据挖掘中用以发现数据分布和隐含模式的一种重要算法, 能简单有效地研究大样本、 多参量和类别未知的光谱数据。 以线指数作为光谱数据的特征值能够在尽可能多的保留光谱物理特征的同时, 有效解决高维光谱数据聚类分析中运算复杂度较高的问题。 本文提出了基于线指数特征的海量恒星光谱数据聚类分析的方法, 提取恒星光谱中的Lick线指数作为海量巡天光谱数据的特征, 使用k均值聚类算法完成对光谱数据的聚类, 然后对聚类结果进行有效的分析。 实验结果证明该方法能够快速有效地将具有相似物理特征的恒星光谱数据聚集到一起, 该方法可以应用到巡天数据的研究中。
Lick线指数; 聚类分析; 恒星光谱
引 言
随着LAMOST[1-3]开始正式巡天, 每天将会观测到上万条光谱数据, 如此庞大的数目对光谱的快速有效处理提出了更高的要求[4-5]。
聚类分析[6]是一种无监督分类方法, 其目的是是把数据对象聚集到不同的子集的过程, 每个子集是一个簇, 簇内的对象彼此非常相似, 而簇间的对象不相似, 一个数据一般只属于一个簇, 簇与簇之间基本上没有交叉。 聚类分析在发现未知群组方面有非常大的作用[7]。
本文提出一种基于Lick线指数特征, 利用k均值算法对海量恒星光谱数据进行聚类分析的方法
1 背景介绍
1.1 Lick线指数
Lick/IDS线指数(简称Lick线指数)是一个相对来说较宽的光谱特征。 Lick线指数定义了25条光学波段的吸收线指数, 包括19条原子吸收线指数以及6条分子吸收线指数。
Lick线指数的计算方式有两种[8], 其中19条原子吸收线指数是以等值宽度的方式计算
(1)
另外6条分子吸收线指数以星等的形式计算
(2)
其中,λ1和λ2分别为中心波段起止波长,FIλ和Fcλ分别表示在中心波段的单位波长的光谱流量与伪连续谱的流量。
文献[8-10]给出了Lick线指数的完整定义及描述。
1.2k均值聚类算法
常用的聚类分析算法[11]包括划分聚类算法、 层次聚类算法、 基于密度的聚类算法、 基于网格的聚类算法,k均值算法(k-means algorithm)是划分聚类算法中的一种。
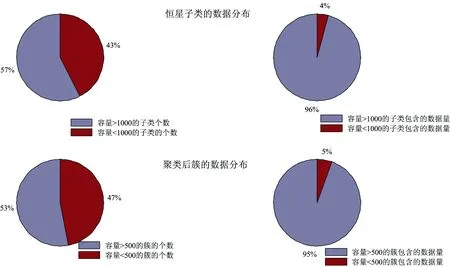
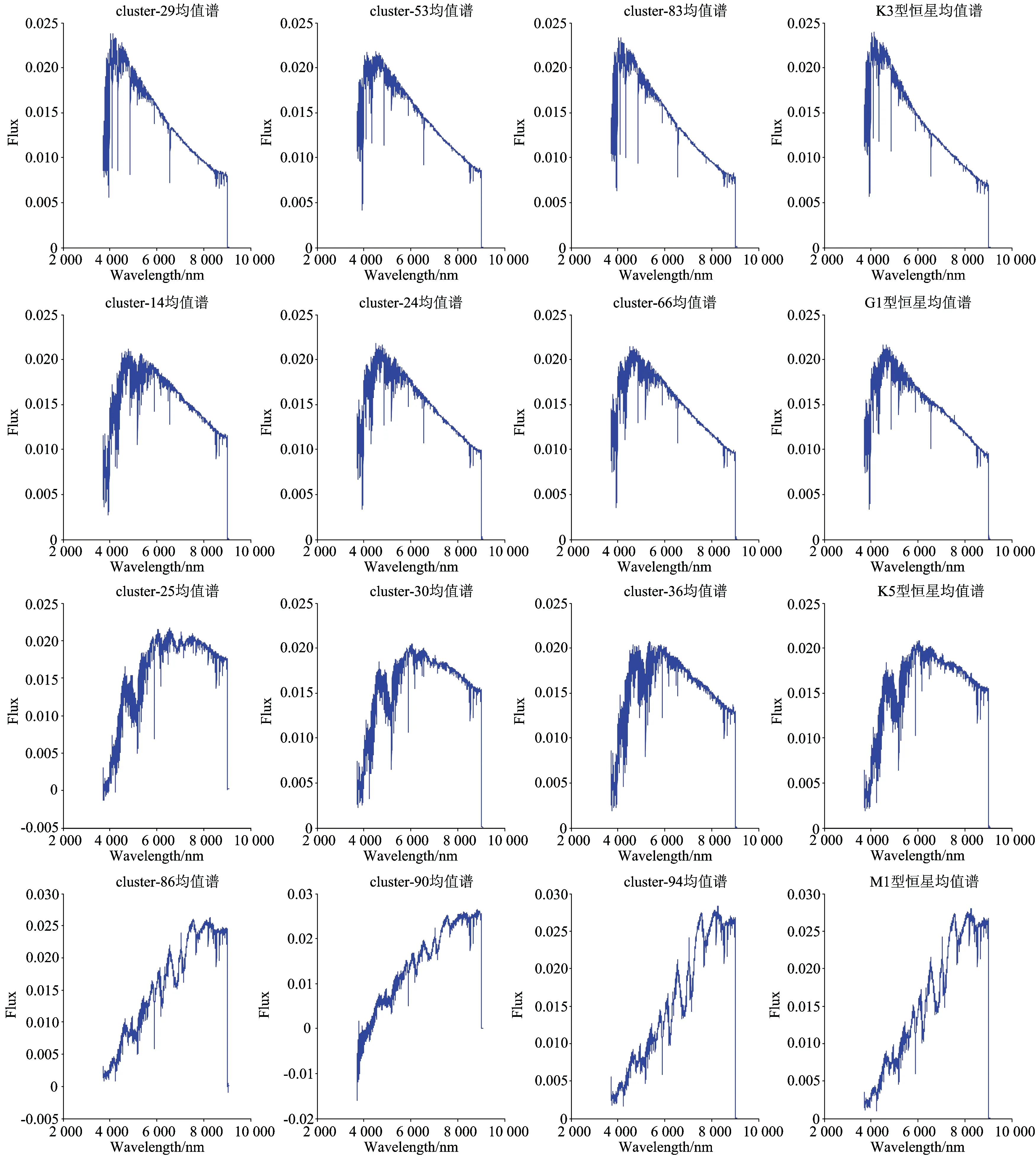
k均值算法[12]的思想是把n个对象根据他们的属性特征划分到k个(k k均值算法首先随机选择k个点作为k个簇的簇心, 剩余的数据按照其与簇心的距离将它们分发到最相似的集合中, 计算每个簇更新后的均值。 这个过程不 断重复, 直到目标函数值达到收敛, 算法描述如下: 输入:k: 簇的数目; D: 包含n个独享的数据集; 输出:k个簇的集合 方法: 1)从D中任意选择k个对象作为初始簇的簇心; 2)repeat; 3)根据簇中对象的均值, 将每个对象(再)指派到最相似的簇; 4)更新簇均值, 即计算每个簇中对象的均值; 5)until 不再发生变化。 本文以Lick线指数作为巡天光谱数据的特征值, 使用k均值聚类算法完成恒星巡天光谱数据的聚类并对实验结果进行了分析。 实验结果证明该方法的聚集结果符合恒星光谱数据的分布规律, 能够将相似的数据聚集到同一个簇中。 表1 实验数据类型分布 2.1 数据 实验选取了10万条LAMOST DR2数据中g波段和r 波段的信噪比大于5的恒星光谱数据。 数据集中包含F型、 G型、 K型以及M型恒星, 具体数量如表1所示。 2.2 步骤 1)读取fits文件中的光谱数据, 并依据上节计算方法计算每条光谱的Lick线指数; 2)对线指数特征进行标准正态分布归一化, 消除不同线指数之间的差异; 3)将恒星光谱类型进行数值化, F0-F9分别取值为0-9, G0-G9取值10-19, K0-K9取值20-29, M0-M9取值30-39; 4)聚类时采用欧式距离, 利用k均值算法对数据进行聚类, 将10万条数据聚为k=100个簇。 3.1 数据分布分析 实验数据集分为F型、 G型、 K型、 M型四种类型, 细分为39个子类。 样本个数大于1 000的子类共有23个, 该23个子类包含全部10万条光谱的95%的数据。 数据的光谱型主要分布大子类中, 剩下较少的数据分布在小子类中。 聚类实验将10万条数据分为了100个簇, 其中样本个数大于500的簇共有53个, 样本个数小于500的簇共计47个。 53个大簇中包括了95%的样本数据点, 剩下5%的数据分布在47个小簇中。 图1列出了数据集的类型分布和聚类结果的分布, 实验结果的分布规律和数据类型的分布规律是一致的, 即数据集中在较大的簇中, 较大的簇和较小的簇数量相差不多。 该方法的聚类效果在数据分布上是符合预期的。 图1 恒星子类分布与聚簇后数据分布对比 3.2 簇内数据相关性分析 计算所有簇中的每个波长采样点的流量平均值, 记为均值谱。 均值谱可辅助分析簇中光谱的物理特征是否明显、 是否一致。 为消除不同光谱尺度上的差异, 在计算均值谱之前, 对所有光谱进行二范数归一化处理。 实验结果中各个簇的均值谱光谱型比较明显、 与模板有较高的拟合度(图2展示了部分簇的均值谱以及对应相似度较高的模板)。 分析可知实验结果中簇内数据具有较为一致的物理特征, 数据之间具有较强的相关性。 图2 部分簇的均值谱图 3.3 光谱型与线指数相关性分析 不同于其他的特征选取方法(PCA, MDS等), 用线指数作为光谱数据的特征值是对光谱在物理意义上的降维。 分析簇中线指数的分布以及簇内数据的物理特征有助于理解线指数与光谱型的相关性。 图3绘制了第69簇和第70簇的均值谱以及线指数的正态参数。 这两个簇的均值谱具有很强的差异性, 线指数的分布是对称的。 统计两个簇数据的子类可以发现69簇主要是K型恒星, 70簇主要为G型恒星。 如图4所示, 第4簇与第9簇也有很大的差异性, 第4簇主要是K型恒星, 第9簇主要为G型恒星。 G4300这根线的线指数能够很好的区分开K型恒星以及G型恒星。 以线指数作为光谱特征值应用到聚类中, 可以充分的保留数据的物理特性, 对聚类结果有很好的帮助。 提出了基于线指数特征的海量恒星光谱数据聚类分析的方法。 该方法提取恒星光谱中的Lick线指数作为海量巡天光谱数据的特征, 使用k均值聚类算法完成对光谱数据的聚类, 然后对聚类结果进行有效的分析。 实验结果证明该方法能够快速有效地将具有相似物理特征的恒星光谱数据聚集到一起, 数据分布符合光谱分布规律, 该方法可以应用到巡天数据的研究中。 图3 第69簇以及第70簇的对比 图4 第4簇以及第9簇的对比 [1] Cui X, Zhao Y, Chu Y, et al. Research in Astron. Astrophys, 2012, 12(9): 1197. [2] Luo A, et al. Research in Astron. Astrophys, 2012, 12(9): 1243. [3] Zhao G, et al. Research in Astron. Astrophys, 2012, 12(7): 723. [4] Wei P, Luo A, Li Y, et al. Monthly Notices of the Royal Astronomical Society, 2013, 431(2): 1800. [5] Wei P, Luo A, Li Y, et al. Astronomical Journal, 2014, 147(5). [6] Jain A K, Dubes R C. Algorithms for Clustering Data. Englewood Cliffs: Prentice Hall, 1988. [7] Jain A K, Murty M N, Flynn P J. Data Clustering: A review. ACM Computing Surveys (CSUR), 1999, 31(3): 264. [8] TAN Xin, PAN Jing-chang, WANG Jie, et al(谭 鑫, 潘景昌, 王 杰, 等). Spectroscopy and Spectral Analysis(光谱学与光谱分析), 2013, 33(6): 1701. [9] Guy Worthey, Faber S M, et al. The Astrophysical Journal Supplement Series, 1994, 94: 687. [10] Trager S C, Guy Worthey, et al. Astrophysical Journal Supplement Series, 1998, 116(1): 1. [11] YAN Tai-sheng, ZHANG Yan-xia, ZHAO Yong-heng, et al(严太生, 张彦霞, 赵永恒, 等). Progress in Astronomy(天文学进展), 2010, 28(2): 112. [12] Hartigan J A, Wong M A. Algorithm AS 136: Ak-Means Clustering Algorithm. Applied Statistics, 1979. 100. *Corresponding author Research on the Clustering of Massive Stellar Spectra Based on Line Index WANG Guang-pei1, PAN Jing-chang1*, YI Zhen-ping1, WEI Peng2, JIANG Bin1 1. School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Weihai 264209, China 2. Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China Clustering algorithm is an important algorithm used to find the data distribution and implicit scheme in data mining. It can study spectra of large amount, multi-parameter and categories unknown simply and effectively. Using lick index as the eigenvalues of spectra can effectively improve the speed to calculate the high-dimensional spectra which can also retain more astrophysical characteristics of spectra. This paper finishes clustering of the survey data withk-means algorithm, using lick index as the eigenvalues of data with finished analysis results. The results show that the new method can gather data with similar physical characteristics together quicker and efficiently, with very good results in discovering rare stars. This method can be applied to the study of Survey data. Lick line index; Clustering; Stellar spectra May 18, 2015; accepted Nov. 23, 2015) 2015-05-18, 2015-11-23 国家自然科学基金项目(U1431102,11473019)资助 王光沛, 1990年生, 山东大学(威海)机电与信息工程学院硕士研究生 e-mail: wangguangpei@live.com *通讯联系人 e-mail: pjc@sdu.edu.cn P145.4 A 10.3964/j.issn.1000-0593(2016)08-2646-052 实验部分

3 结果与讨论
3 结 论


