药品近红外光谱通用性定量模型评价参数的选择

冯艳春， 张 琪， 胡昌勤

中国食品药品检定研究院， 北京 100050

药品近红外光谱通用性定量模型评价参数的选择

冯艳春， 张 琪， 胡昌勤*

中国食品药品检定研究院， 北京 100050

为寻找药品近红外通用性定量模型在建立过程中用于确立最优模型的关键评价参数组合， 收集整理了目前各种商品化化学计量学软件及文献中的13个常用于评价近红外定量模型的统计学参数， 结合人用药品注册技术要求国际协调会对于药品定量分析方法验证基本要求， 对92个药品近红外通用性定量分析模型的这些参数进行了计算和分析。 通过对各个参数之间相互关系的研究， 确定了适合于药品近红外通用性定量分析模型评价的参数组合， 并统计出了这些参数的数值范围： 用于模型准确性评价的关键参数为交叉验证均方根误差/预测均方根误差、 平均相对偏差和相对分析误差； 大部分交叉验证均方根误差/预测均方根误差结果在3%以内， 其中交叉验证均方根误差在数值上与平均绝对偏差相当， 大部分相对分析误差值大于2， 而平均相对偏差的数值与所建模型的类型(剂型、 样品的包装形式)和待测成分含量的分布有关。 模型线性评价关键参数为决定系数； 大部分模型的决定系数在80%～100%之间。 模型耐用性关键评价参数为预测均方根误差与交叉验证均方根误差的比值， 大部分模型该参数在1.5以内。 精密度评价关键参数为重复测定结果的标准差； 该参数对于规范近红外的操作， 以及考核模型能否在不同仪器间传递具有重要的意义， 但目前药品近红外通用性定量模型对于分析精密度的关注较少， 无法估计出具体数值范围。 该研究不仅为药品近红外通用性模型的建立者和使用者提供了评价模型优劣的依据， 也为完善药品近红外光谱通用性定量分析模型的参数评价体系提供了基础数据。

药品； 近红外光谱； 通用性定量模型； 模型优化； 评价参数； 准确性； 线性； 精密度； 耐用性

引 言

为有效打击我国市场上的假劣药品， 中国食品药品检定研究院从2003年起着手开展药品近红外(near infrared， NIR)快速分析系统地研究[1]； 2006年起该系统被装备于药品检测车上， 用于流通领域药品质量的快速筛查[2]， 逐步形成了国内NIR分析技术的一个主要应用平台[3]。 其中药品NIR通用性定量分析模型是该系统的重要组成部分， 该类模型由于涵盖了不同厂家、 不同仪器所测样品的光谱信息， 因此能有效排除制剂中工艺、 辅料的干扰， 针对活性成分对不同企业的具有相同INN(international nonproprietary names)名称的同类产品在销售现场进行快速定量分析。 有关如何建立该类模型已经进行过详细的报道， 同时很多药品通用性定量模型也已投入使用[4]， 但对于如何系统地评价该类模型还鲜有报道。

NIR光谱技术属于二级分析方法， 定量模型需要一定数量的代表性样品， 借助软件将法定方法测得的含量与样品的NIR光谱图进行关联， 通过多元校正的方法建立模型用于预测未知样品。 在建模过程中， 通常要尝试不同的光谱预处理方法， 选择不同的谱段与待测成分的含量进行关联， 以获得理想的模型， 即模型优化； 且需要借助于适宜的评价参数确定最优模型。 虽然人用药品注册技术要求国际协调会(International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use, ICH) 颁布的分析方法验证指南ICH Q2 (R1)中已经对药品定量分析方法的评价提出了基本要求， 但基于多元校正方法的NIR定量模型的优化过程运算十分巨大， 因此一般都需要依赖于计算机仅使用来自NIR仪器随机携带或商品化的化学计量学软件中的参数用于模型优化过程的评价。 然而这些参数并不足以完全的评价或验证模型的优劣， 进行NIR模型的评价和验证应以适合于最终使用为目标， 根据应用目的， 恰当的选择评价参数和评价方法[5]。 基于ICH的基本原则和建立药品NIR通用性定量分析方法的特殊性， 选择模型合适的评价参数就显得十分重要。 本文总结归纳了目前各种商品化化学计量学软件及文献中常用的评价NIR定量模型的统计学参数， 同时结合ICH Q2 (R1)中对药品定量分析方法验证的基本要求， 以92个药品NIR通用性定量模型为例， 分别计算、 统计、 分析和比较目前常用的NIR定量模型评价参数， 系统地揭示药品NIR通用性定量分析模型的特征， 并尝试寻找到适宜的评价药品NIR通用性定量分析模型的最佳参数组合， 为建立药品NIR通用性定量分析模型评价体系提供基础数据。

1 实验部分

1.1 参与数据统计的药品NIR通用性定量分析模型

共收集到92个药品NIR通用性定量模型进行各个参数的计算、 分析和评价。 其中包含2个注射液模型(分别为硫普罗宁和左氧氟沙星小针剂)； 19个注射用粉针模型(分别为阿莫西林钠、 氨苄西林钠、 氨苄西林钠舒巴坦钠、 更昔洛韦、 泮托拉唑钠、 普鲁卡因青霉素、 青霉素钠、 头孢呋辛钠、 头孢拉定、 头孢美唑钠、 头孢哌酮钠、 头孢哌酮钠舒巴坦钠、 头孢曲松钠、 头孢噻肟钠、 头孢唑林钠、 头孢唑肟钠)； 10个注射用粉针水分模型(分别为氨苄西林钠舒巴坦钠、 氨苄西林钠、 普鲁卡因青霉素、 头孢呋辛钠、 头孢美唑钠、 头孢哌酮钠舒巴坦钠、 头孢曲松钠、 头孢噻肟钠、 头孢唑林钠、 头孢唑肟钠)； 8个非铝塑胶囊剂模型(分别为阿莫西林、 布洛芬、 利福平、 罗红霉素、 诺氟沙星、 头孢拉定、 盐酸雷尼替丁、 盐酸左氧氟沙星)； 7个铝塑胶囊剂模型(分别为阿莫西林、 枸橼酸铋钾、 罗红霉素、 诺氟沙星、 洛伐他汀、 盐酸克林霉素、 盐酸左氧氟沙星)； 38个非铝塑片剂模型(分别为阿卡波糖、 阿莫西林克拉维酸钾、 阿奇霉素、 阿司匹林、 氨茶碱、 贝诺酯、 吡嗪酰胺、 对乙酰氨基酚、 呋喃唑酮、 格列吡嗪、 格列齐特、 谷维素、 红霉素、 琥乙红霉素、 甲硝唑、 卡托普利、 利巴韦林、 罗红霉素、 尼莫地平、 尼群地平、 青霉素V、 氢氯噻嗪、 维生素B1、 维生素B2、 维生素B6、 维生素C、 西咪替丁、 硝苯地平、 辛伐他汀、 盐酸氨溴索、 盐酸苯海索、 盐酸吡格列酮、 盐酸地尔硫卓、 盐酸二甲双胍、 盐酸左氧氟沙星、 氧氟沙星、 异烟肼)； 8个铝塑片剂模型(分别为阿奇霉素、 苯磺酸氨氯地平、 对乙酰氨基酚、 利巴韦林、 盐酸氨溴索、 盐酸地尔硫卓、 盐酸左氧氟沙星、 氧氟沙星)。

所有NIR光谱模型的参考方法均采用中国药典或部(局)颁药品标准等国家法定标准中收载的该品种的含量测定方法。 NIR光谱的采集均使用布鲁克公司的MATRIX-F， MPA或TENSOR37型傅里叶变换型光谱仪， 所有仪器光路相似， 且均配有1.5 m的光纤探头用于漫反射采样。 同时， 针对不同药品剂型， 光谱采集的关注点不同[6]： 对于注射用粉针剂， 直接用光纤探头抵住玻璃瓶底较平整部位测量； 对于液体制剂， 采用附件在光纤探头前固定形成测样槽， 将少量待测液滴加至测样槽中进行测量； 对于片剂， 按包装形式分为铝塑包装和非铝塑包装(瓶装和铝铝包装)样品， 非铝塑包装样品， 从包装中取出后用光纤探头抵住测量， 铝塑包装样品无需拆除包装， 用光纤探头直接隔塑料包装一侧抵住测量， 测量位点尽量选择片剂无刻痕一面； 对于胶囊剂， 包装分类和测样方式基本与片剂相同， 只是探头测量位点尽量选择单层胶囊壳一端。

1.2 评价参数与特性

在建立NIR光谱定量模型的过程中， 通常需要对NIR光谱预测结果和参照方法测定结果进行统计分析， 以评价所建模型的质量， 从而确定最优模型参数并对模型的实用性作出初步的判断。 模型建成后， 还需要按照ICH的要求对模型从方法的准确性、 精密度、 专属性、 线性、 范围和耐用性等方面进行验证， 以证明方法适合于相应的检测要求。 因此， 无论是模型关键评价参数的选择还是最优模型的确定都应为进一步的方法验证打下良好的基础。

1.2.1 准确性参数

对于NIR定量模型， 方法的准确性往往倍受关注。 评价NIR模型预测准确性的实质就是评价NIR预测结果与样品参照结果的接近程度。 模型优化时， 主要通过比较误差参数在优化过程中的变化， 确定最优模型； 建模时如设有验证集， 则应首选验证集的误差参数进行比较， 如无验证集， 也可以利用训练集进行比较。 方法验证时， 则主要比较NIR模型对与训练集完全独立的验证集样本的预测结果与参照结果之间是否有显著性差异。 目前主要的误差评价参数如下：

1.2.1.1 偏差(Bias)

偏差， 即NIR预测值(Y)与参照值(X)之差。 在模型评价中的偏差一般指平均偏差， 计算公式见式(1)， 用于表征NIR校正模型的总体准确性[7]。

(1)

式中，n为训练集或者验证集的样本数量。 以下公式中X，Y和n的意义与此相同。

1.2.1.2 SECV和SEP

交叉验证标准误差(standard error of cross-validauion， SECV)和预测标准误差(standard error of prediction， SEP)均表征NIR结果与参照结果差异的标准差[7]， 但SECV表示的是训练集样本交互验证的标准差， 而SEP是模型对验证集样本的预测标准差， 两者计算公式见式(2)

(2)

1.2.1.3 RMSECV和RMSEP

交叉验证均方根误差(root mean square error of cross-validation， RMSECV)和预测均方根误差(root mean square error of prediction， RMSEP)均表征NIR结果与参照结果差异的标准误差[7]， 但RMSECV表示训练集样本交互验证结果的标准误差， 而RMSEP表示模型对验证集样本预测结果的标准误差， 两者计算公式见式(3)。 部分文献中使用n-1做分母， 当n→∞时， (n-1)/n→1， 所以当样本足够大时， 对结果影响不大。 RMSECV/RMSEP中包含有偏差的信息， 如果偏差为0， RMSECV/RMSEP与SECV/SEP一致， 但当偏差存在时， RMSECV/RMSEP要明显大于SECV/SEP。 从式(3)可以看出， 虽然RMSECV/RMSEP与偏差有关， 但并不能暗示偏差的大小和特征， 因此， 标准误差和偏差都经常用于评价模型的准确性。

(3)

1.2.1.4 RPD

Williams等[8]于1993年提出用相对分析误差[ratio of (standard error of) prediction (validation) to (standard) deviation， RPD]参数来评价NIR定量模型的准确性， 现已成为农业领域评价模型有效性使用频率最高的参数之一。 通常要求RPD为5或者更高[9]。 其计算公式见式(4)， SDx为验证集样本参照结果的标准偏差； 如采用交叉验证方法评价， RPD为训练集样本参照值的标准偏差与SECV的比值。 RPD是一个简单的可以对SEP进行评价的统计量。 SEP应该远低于SDx， 如果SEP值与SDx相等或者大于SDx值， 就意味着方法无法准确预测参照值。

RPD=SDx/SEP

(4)

1.2.1.5 RER

浓度范围与预测(交叉验证)标准误差的比值[ratio of the SEP(SECV) to the range， RER]是Starr等提出的将SEP与参照值浓度范围相关， 建立的另外一个标准化的SEP评价指标[10]， 其计算公式见式(5)。 RER值应该越大越好， 但其易受参照值个别数据的影响， 一个极值参照就可能导致RER值升高， 因此要求参照数据的浓度范围呈均匀分布。

(5)

1.2.1.6 相对偏差

除了以上参数之外， 在药品通用性定量模型中， 为了更加直观地比较预测结果与参照结果之间的差异， 引入相对偏差(relative deviation)的概念[11]， 其计算公式见式(6)。 相对偏差表示每一个NIR预测结果与对应的参照结果的差异占参照结果的百分比。 与常规的相对偏差[12]表示的意义不同， 式(6)中Xi不再代表对某一样品多次测量的平均值， 而是代表第i个样品的参照结果。 一般通用性模型训练集或者验证集中样品间的浓度差异较大， 采用相对偏差可以减少浓度对预测偏差的影响。 为了表征NIR训练集或者验证集样本的总体偏差， 使用平均绝对偏差[average absolute deviation, AAD, 式(7)]和平均相对偏差[average relative deviation, ARD, 式(8)]， 式中ARD使用相对偏差的绝对值进行计算。

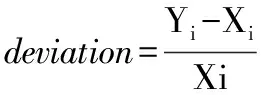
(6)

(7)

(8)

1.2.2 线性参数

NIR模型的线性与传统分析方法的线性不同。 由于NIR模型一般采用多元回归法建立， 所以它的线性通常由待分析物的预测结果与参照结果之间的关系表征； 而线性范围， 表征模型能达到一定精密度、 准确性要求时高低限浓度或量的区间， 主要由建模训练集样本的浓度范围决定。 因此， 线性也可以间接反映NIR定量模型的准确性。 但与上述准确性参数所表征的意义不同： 误差分析主要表征NIR预测结果与参照结果之间的误差大小， 而线性主要表征NIR方法与参照方法之间的相关性。 只有当NIR方法与参照方法之间具有明确的相关性， 且NIR预测结果与参照结果之间的误差在可接受范围， NIR方法才具有实用价值。

方法验证时主要关注验证集样本预测结果与参照结果所得直线的截距、 斜率、 相关系数和决定系数。 模型优化时也可以用训练集样本的交叉验证结果代替。

1.2.2.1 相关系数r和决定系数R2

r(correlation coefficient)表征两组数据(即参照结果和NIR预测结果)彼此间的相关程度[12]， 其计算公式见式(9)。 当r=1时， 两组数据完全相关。 由于无论是X或Y都可能产生误差， 因此，X和Y可能呈正或负相关。

R2(determination coefficient)是以回归偏差占总偏差的比率来表示回归模型的拟合优度[13]， 计算公式见式(10)。 可以推导出当X与Y线性相关时， 决定系数为相关系数r的平方， 即决定系数R2同相关系数r具有一致性。 如果R2=90%， 则表示总偏差中的90%可以由X和Y的依存关系来解释， 只有10%属于随机因素(如样品制备， 参照方法测试等)。 当R2=50%时，r=71%， 虽然此时随机因素的影响已经有50%， 但X和Y的依存关系仍占主导地位， 这是可以接受结果的底线[14]。 另外决定系数也可以写成式(11)， 式中SDc为训练集浓度值的标准偏差[式(12)]。 可以看出R2的大小与浓度分布范围有关， 相同的RMSECV， 浓度分布范围越宽(SDc越大)，R2也越大[15]。 因此采用R2表征NIR定量模型的相关关系较r可以得到更多的有用信息。

(9)

(10)

(11)

(12)

1.2.2.2 回归系数和截距

回归系数(regression coefficient，b)也被称为斜率， 通常b和截距(intercept，a)共同用来表征Y值能被X值准确预测的程度[8]， 其计算公式见式(13)和(14)。b和a通常和r一起用于从整体上评价NIR结果与参照结果两组数据是否具有相关性。 由于存在误差， NIR结果与参照结果的拟合方程通常呈Y=bX+a的形式。 当两种方法存在系统误差(b=1，a≠0)时， 如果r=1， 且系统误差在可接受的范围时， NIR方法仍然可被接受； 但如果参数b≠1且与1相差较大， 则表示NIR预测结果与参照方法之间不存在相关性， 此时参数r明显小于1， NIR预测结果的准确性受到质疑。 上述分析也提示参数r较参数b和a更加重要。

(13)

(14)

1.2.3 精密度参数

精密度主要指在规定条件下， 同一份均匀供试品， 经多次取样测定所得结果之间的接近程度。 对于NIR方法精密度的评价， 主要包含两方面： 一是指在同一实验室， 由同一操作者使用相同的仪器设备， 按照相同的测试方法在短时间内对同一被测样品相互独立进行测试(重复性)； 二是指在不同实验室， 由不同操作者使用不同的仪器设备， 按相同的测试方法对同一被测样品相互独立进行测试(重现性)。 一般用测定结果的标准偏差(SD)来表征精密度， 计算公式如式(12)， 其中X代表重复测量的结果。

1.2.4 耐用性参数

耐用性系指当测定条件有小的变动时， 方法所能承受的保证测定结果不受影响的程度。 NIR光谱， 特别是液体样品的NIR光谱受环境等因素的影响较大。 NIR模型的耐用性主要指模型应对样品光谱变动的适应性质， 它表示了测量中模型允许光谱的变异范围： 耐用性较好的模型应对样品光谱变动的适应能力较强， 反之较差。 对于药品NIR通用性定量分析模型， 训练集样本的代表性与模型的耐用性息息相关。 对在建模中同时存在训练集和验证集的模型， 通过对训练集样本参照数据的均值和标准偏差与验证集样本的结果进行比较， 可以判断训练集和验证集的样本是否来自相同的总体且具有相同的代表性。 另外国际谷物化学组织(International Cereal Chemists, ICC)在2001年公布的通用标准化NIR分析推荐草案《No. 202. General Recommendation for Standardization Near Infrared Analysis (Draft 2001)》， 简称ICC标准)中， 将SEP/SEC作为稳健性评价的指标性参数， 规定在正常的容变性范围之内， 该值应小于1.2， 其值大于1.2则表示模型稳健性不佳。

1.2.5 专属性参数

NIR方法的专属性主要指模型识别分析物是否为特定分析对象的能力。 在NIR分析方法中， 除了常规的比较PLS载荷因子与活性成分光谱之外， 也常采用马氏距离来评判一个模型的专属性。 目前， 国内外尚未见直接用于评价模型专属性的公认参数。 但由于药品NIR通用性模型通常与定性模型串联使用， 只有定性判别为此品种的药品才应用相应的定量模型。 所以专属性本身对于这类模型来说目前不是关键评价指标。

2 结果与讨论

2.1 各参数之间的关系

2.1.1 RMSECV与SECV， RMSEP与SEP相关性

通过计算92个模型交叉验证和外部验证结果， 得到RMSECV(x)与SECV(y)的相关性方程为y=1.007 6x+0.000 6(r=0.999 9)， RMSEP(x)与SEP(y)的相关性方程为y=1.011 7x-0.011 2(r=0.999 7)。 由于所有模型的预测偏差均较小， 故SECV(SEP)和RMSECV(RMSEP)几乎相等， 两者的r值均大于0.999； 此时， 只需使用其中的一个参数就可以表征模型的预测误差。

2.1.2 RMSECV与AAD相关性

实验结果显示， 各模型训练集样本AAD在数值上与RMSECV相当， 略低于RMSECV(图1)， 并和RMSECV(x)呈很好的线性关系(y=0.786 2x-0.004 5，r=0.995 9)。 验证集的AAD与RMSEP也呈类似关系。 由于AAD在一般商业化软件中不能直接得到， 因此在使用过程中可以用RMSECV或者RMSEP来预测AAD较为方便。

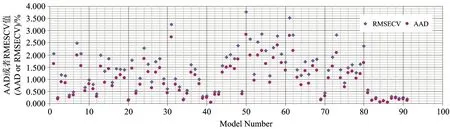
图1 92个模型训练集的RMSECV与平均绝对偏差

2.1.3 RMSECV/RMSEP与ARD相关性

通用性定量模型由于所针对的预测对象是来自不同企业的相同药品， 药品处方和规格的差异使得不同的样品， 单位质量中药品活性成分的量可能有较大的差异。 因此尽管样品的绝对偏差可能一致， 但其相对偏差可能相差较大。 从图2可以看出， ARD和RMSECV/RMSEP没有显著的相关性。 因此在评价通用性定量模型时， 逐一计算验证样本的相对偏差以及整体的ARD可更有效地表征模型的预测能力。

图2 ARD与RMSECV(a)/RMSEP(b)关系图

2.1.4 RMSECV与R2相关性

选择剂型、 包装相同的通用性模型如2.1.3中作图的方法比较模型R2与RMSECV的关系。 结果39个非铝塑包装片剂通用性模型的R2与RMSECV没有明显线性关系。 即对于不同的训练集样本来说， 不能单凭R2的大小来评价模型的准确性。 对于同一训练集样品， 由于R2越大， NIR预测结果与参照结果之间的误差越小， NIR方法与参照方法之间的相关性越强， 因此R2用来评价使用相同训练集样本优化模型时， 是一个很好的模型评价参数。 但R2不能单独用来评价不同训练集所建立的不同模型的质量。

2.1.5 RPD与RER，R2和RMSECV相关性

RPD和RER都是无量纲的评价参数， 它们不仅可以作为模型优化时的评价参数， 也可以用于不同模型的横向比较。 由于， 验证集或训练集中样品分布的SD或样品浓度范围可表征样品参比值的范围， 因此这两个参数还可表征NIR模型对于含有不同待测量样品的分辨能力[16]。 模型的分辨能力与被分析物含量跨度范围大小有关， 当不同的训练集样品参比值有相同的均值和SEP时， 含量跨度越大， 模型对未知样品预测结果的可修正范围越大， 模型对不同预测样品的分辨能力更强， 预测结果更准确。 和RPD相比， RER易受样品极值浓度的影响， 因此RPD更为常用。

如果建模数据呈正态分布， RPD还可以写成式(15)， 可见虽然RPD会随R2的增加而增加， 但当R2接近100%时， RPD值仍有较大的变化。 一般认为R2大于0.75， 即RPD大于2时， 模型已达到可接受程度。

(15)

另外， 通过如2.1.3中的作图方法分析， RPD与RMSECV的相关性较小， 是两个相对独立的量， 故二者可能不一致。

2.2 关键评价参数的选择和数值范围统计

2.2.1 准确性参数

2.2.1.1 偏差

图3为92个模型交叉验证和外部验证结果偏差的正态分布图(受样品量的影响， 只有35个模型存在外部验证结果)， 交叉验证的偏差基本分布在±0.1%之间， 而外部验证的偏差分布在±0.5%之间。 由于交叉验证时所有的样本均来自同一个整体， 故得到的偏差结果偏低， 并不能很好的反映出模型预测偏差的真实特征。 实际应用中药品NIR通用性模型主要用于筛查含量远低于标示含量的假药， 因此无论是0.1%或0.5%的差异都是微不足道的。 故这个参数可以不作为药品NIR通用性模型的关键评价参数。

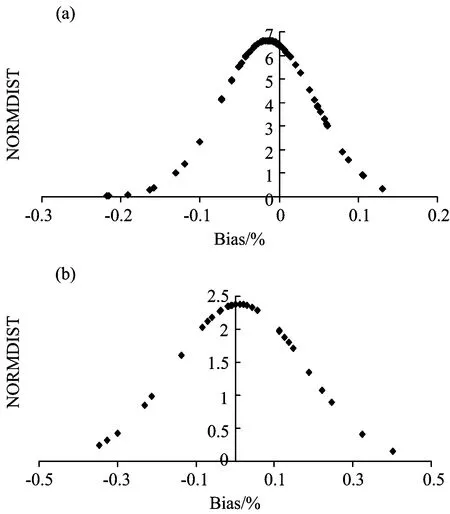
图3 偏差结果概率密度函数图

2.2.1.2 RMSECV/RMSEP

由前面对各参数关系特性的分析可知， 当预测偏差不能忽略时， RMSECV/RMSEP要明显大于SECV/SEP， 对模型的预测偏差更敏感， 故更推荐使用RMSECV/RMSEP表征模型的预测误差。 统计所有92个模型的RMSECV和RMSEP结果发现， 除5个结果外， 其他结果均在3%以内， 提示如果所建模型的RMSECV/RMSEP大于3%， 需要仔细研究寻找原因。

2.2.1.3 ARD

由于ARD和RMSECV/RMSEP没有显著的相关性， 故通常二者不能任选其一， 因此ARD也是药品通用性定量分析模型必不可少的评价参数之一。 本文共对10个注射用粉针剂水分含量模型进行了分析， 所有训练集和验证集共包含804个样品， 通过留一法交叉验证和验证集外部验证共得到804个NIR预测结果， 以相对偏差来表示对每一个样品预测的误差(表1)， 可见注射用粉针剂水分含量均在10%以下， 随着水分含量的升高， 预测ARD逐渐减小。

表1 注射用粉针剂水分含量预测结果相对偏差分析

同理对19个注射用粉针剂活性成分定量模型所涉及到的1743个样品的NIR预测结果与参照结果进行了比较(表2)。 由于注射用粉针剂中的辅料相对于其他剂型要少， 因此活性成分含量相对较高， 同时可见当含量高于60%时， 尽管NIR的测量方式是隔着玻璃瓶测量， 但其分析ARD小于2%。 对38个非铝塑包装片剂定量分析模型所涉及到的3 590个样品的NIR预测结果与参照结果进行了分析(表2)。 样品的参照结果均大于2%， 大多数含量在10%至80%之间。 与注射用粉针剂预测模型相比较， 在相同的浓度范围， 不管是水分模型还是活性成分预测模型， 片剂预测结果的ARD都大于注射用粉针剂预测结果的ARD。 由于片剂成分的复杂程度远大于注射用粉针剂， 提示通用性NIR模型的预测准确性不仅与模型的预测范围有关， 还和待测成分的复杂程度有关。 对8个非铝塑包装胶囊剂定量分析模型所涉及到的841个样品的NIR预测结果与参照结果进行比较(表2)， 可见， 由于受到胶囊壳的干扰， 即使是去除铝塑包装直接使用光纤测量胶囊剂， 在同一含量范围内， 胶囊剂测量ARD明显高于注射用粉针剂和片剂的活性成分。

表2 各剂型活性成分含量预测结果相对偏差分析

Table 2 The ARD analysis of the universal quantitative models in the different formulations for their corresponding APIs (active pharmaceutical ingredient)

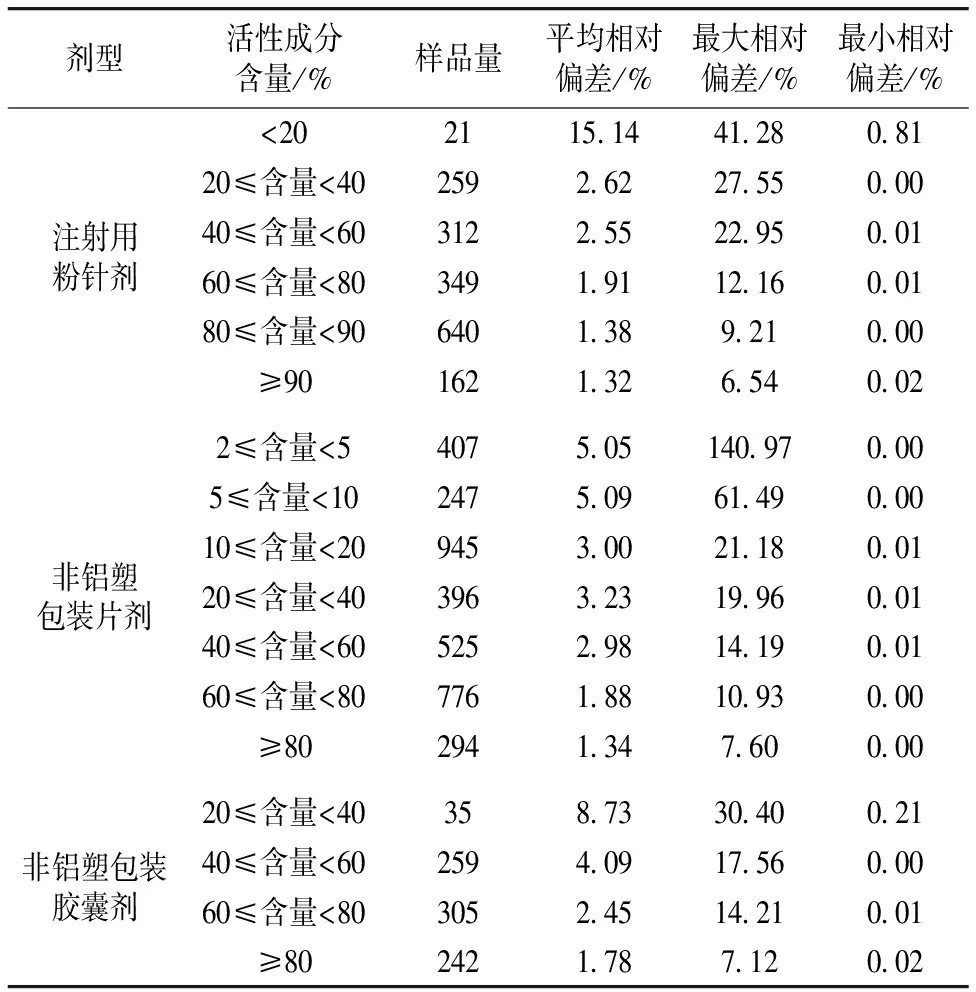
剂型活性成分含量/%样品量平均相对偏差/%最大相对偏差/%最小相对偏差/%注射用粉针剂<202115 1441 280 8120≤含量<402592 6227 550 0040≤含量<603122 5522 950 0160≤含量<803491 9112 160 0180≤含量<906401 389 210 00≥901621 326 540 02非铝塑包装片剂2≤含量<54075 05140 970 005≤含量<102475 0961 490 0010≤含量<209453 0021 180 0120≤含量<403963 2319 960 0140≤含量<605252 9814 190 0160≤含量<807761 8810 930 00≥802941 347 600 00非铝塑包装胶囊剂20≤含量<40358 7330 400 2140≤含量<602594 0917 560 0060≤含量<803052 4514 210 01≥802421 787 120 02

另外， 在92个模型中有7个片剂品种和4个胶囊剂品种用同样的样品既建立了铝塑包装模型又建立了非铝塑包装模型。 比较同一品种药品的这两种模型， 发现总体上铝塑包装模型的各项统计参数略差于非铝塑包装的结果， 证明塑料包装可影响预测结果的准确性。

2.2.1.4 RPD

92个模型的RPD有86个在2以上， 42个在5以上， 且由于通用性模型涉及不同生产工艺的同种产品， 样品处方的差异使得其含量的跨度较大， 因此个别模型RPD值更高。

2.2.2 线性参数

评价模型线性的参数主要有R2，r，a和b。 由前面的原理介绍和关系分析可知， 更倾向于使用R2来评价NIR模型的准确性， 且与其他几个参数相比，R2可由多数NIR商业化软件直接给出， 无需再另外计算。 经统计92个模型， 大部分R2集中在80%～100%之间， 也有个别模型的R2只有20%， 但并不影响模型的预测能力。 同样说明R2不宜单独用来评价不同训练集所建立的不同模型的质量。

2.2.3 精密度参数

模型精密度评价对于规范NIR的操作， 以及考核模型能否在不同仪器间传递具有重要的意义。 ICC标准规定同一样品在同一仪器多次测定计算的预测精密度标准差要小于等于0.5×SEP， 另一国际组织美国谷物化学家协会(American Association of Cereal Chemists, AACC)在其批准的方法(《AACC Method 39-00 Near-Infrared Methods——Guidelines for model Development and Maintenance》， 简称AACC标准)中规定该值应小于等于0.33×SEP， 即重复性标准差大约占SEP的1/2～1/3； ICC标准规定模型在同一品牌仪器的子机之间传递时， 定标模型传递的标准差要小于等于0.7×SEP(AACC标准则定为0.5×SEP)。 由于SEP不但包含了光谱测量与参比值测量产生的随机误差、 系统误差， 还包含模型稳健性不足产生的偏差以及信息处理过程中产生的误差， 因此NIR方法的精密度(SD)和参照方法的精密度(SD)应低于SEP； 且NIR方法本身的精密度可能好于参照方法。 以往在药品NIR通用性模型的建模过程中， 对精密度的关注较少， 特别是同一样品在同一实验室的重复测定结果， 因此目前没有足够的数据精确估算重复性与SEP的关系。 对于个别品种， 曾经进行过不同仪器间模型传递精密度的考察， 比如琥乙红霉素和罗红霉素片剂的通用性定量分析模型[11](表3)， 可见由于RMSEP与SEP结果相近， 因此精密度与SEP的关系可以用精密度与RMSEP的关系代替。 对琥乙红霉素片剂模型， 13个样品分别在7台不同仪器上测定结果的重现性均小于0.5RMSEP， 对罗红霉素片剂模型， 尽管大部分结果小于0.7RMSEP， 但有一批样品的结果大于SEP(该批样品的含量为31%左右)， 可见不同仪器间的再现性不仅与被测样品的浓度有关， 还可能与被测品种的复杂程度(处方、 工艺)有关。

2.2.4 耐用性参数

92个模型中只有35个模型存在独立的验证集。 在建立NIR通用性模型时， 由于样品量的限制， 为保证训练集的代表性， 往往训练集样本所包含的变异要多于验证集， 即目前的35个验证集不能保证包含与训练集完全相同的独立样本。 因此一般情况下， 训练集样本的SDc会大于验证集样本的SDx， 如果出现相反的情况， 则提示训练集样本的代表性不全。 实验结果表明35个模型中， SDx大于SDc的模型有21个， 剩余的14个模型中， 有7个模型的SDx与SDc相对偏差小于10%， 与理论分析结果基本一致。

表3 琥乙红霉素、 罗红霉素非铝塑片剂模型传递统计结果

Table 3 The statistical results of transferability for the universal quantitative model for determination of erythromycin ethylsuccinate or roxithromycin in tablets without blister packing

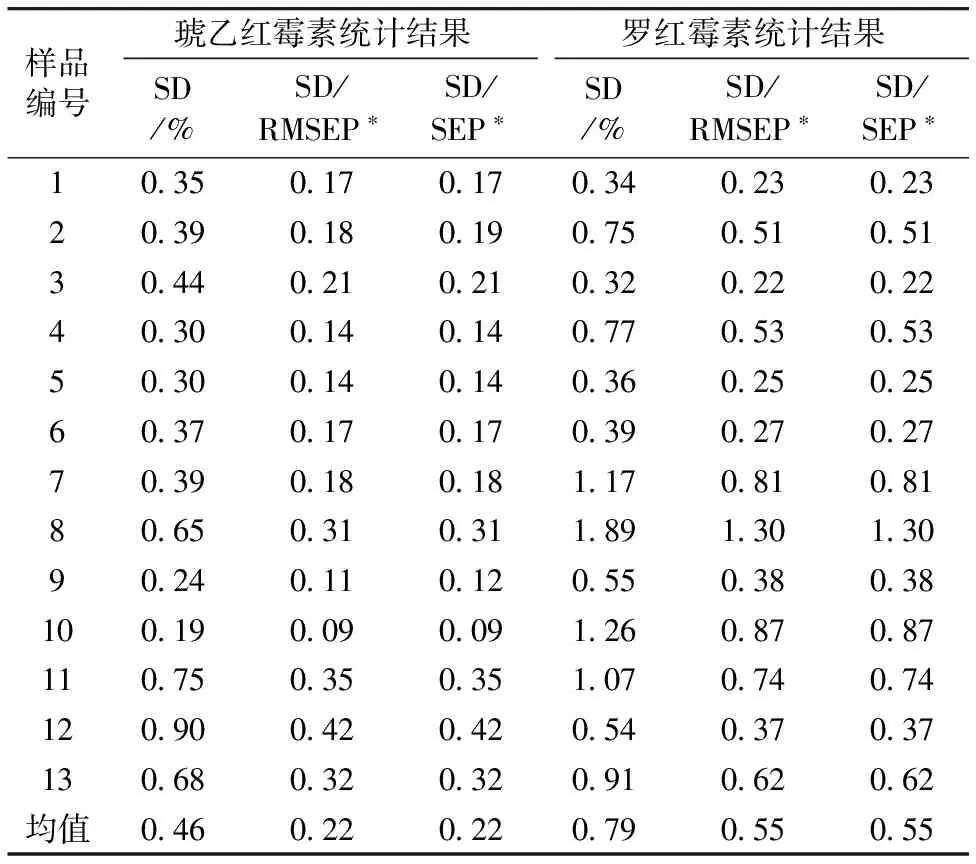
样品编号琥乙红霉素统计结果罗红霉素统计结果SD/%SD/RMSEP∗SD/SEP∗SD/%SD/RMSEP∗SD/SEP∗10 350 170 170 340 230 2320 390 180 190 750 510 5130 440 210 210 320 220 2240 300 140 140 770 530 5350 300 140 140 360 250 2560 370 170 170 390 270 2770 390 180 181 170 810 8180 650 310 311 891 301 3090 240 110 120 550 380 38100 190 090 091 260 870 87110 750 350 351 070 740 74120 900 420 420 540 370 37130 680 320 320 910 620 62均值0 460 220 220 790 550 55

*琥乙红霉素模型： RMSEP=2.13%, SEP=2.12%； 罗红霉素模型： RMSEP=1.45%, SEP=1.45%

*The model for erythromycin ethylsuccinate: RMSEP=2.13%, SEP=2.12%; The model for roxithromycin: RMSEP=1.45%, SEP=1.45%

由2.1.1可知SECV(SEP)和RMSECV(RMSEP)几乎相等， 因此本研究计算了所有35个模型RMSEP与RMSECV的比值， 均在1.5以内。

3 结 论

研究表明， 在建立药品NIR通用性定量分析模型过程中， RMSECV/RMSEP， ARD， RPD，R2， 重复测定结果的SD和RMSEP与RMSECV的比值6个参数是模型优化过程中的关键评价参数， 利用这组参数可从模型的准确性、 线性、 精密度和耐用性四个方面对模型进行全面的表征。

通过对92个药品NIR通用性定量分析模型参数值的统计， 发现大部分模型的RMSECV/RMSEP在3%以内， 其中RMSECV在数值上与AAD相当； RPD值大于2； ARD的数值与模型的类型(剂型、 样品的包装形式)和待测成分的含量分布有关；R2在80%～100%之间； RMSECV与RMSEP的比值在1.5以内。 另外研究还提示， 目前对药品NIR通用性定量分析模型精密度的关注较少； 由于该参数对于规范NIR操作， 考核模型能否在不同仪器间传递具有重要的意义， 应在以后的建模过程中予以关注。

本研究结果不仅药品NIR通用性模型的建立者和使用者提供了评价模型优劣的依据， 也为完善药品NIR通用性定量分析模型的参数评价体系提供了基础数据。

[1] HU Chang-qin, FENG Yan-chun(胡昌勤, 冯艳春). Chinese Pharmaceutical Affairs(中国药事), 2004, 18(4): 250.

[2] HU Chang-qin, FENG Yan-chun, XUE Jing, et al(胡昌勤, 冯艳春， 薛 晶， 等). Chinese Journal of Pharmaceutical Analysis(药物分析杂志), 2008, 28(4): 647.

[3] Chu X L, Lu J. NIR News, 2014, 25(6): 13.

[4] Hu C Q, Feng Y C, Yin L H. J. Near Infrared Spec., 2015, 23: 271.

[5] De Bleye C, Chavez P F, Mantanus J, et al. J. Pharmaceut. Biomed., 2012, 69: 125.

[6] HU Chang-qin, FENG Yan-chun(胡昌勤， 冯艳春). Near Infrared Spectroscopy for Rapid Drug Analysis(近红外光谱法快速分析药品). Beijing: Chemical Industry Press(北京： 化学工业出版社), 2011. 106.

[8] Williams P C, Sobering D C. J. Near Infrared Spec., 1993, 1: 25.

[9] Williams P C, Norris K. Near-Infrared Technology in the Agricultural and Food Industries. Saint Paul: American Association of Cereal Chemists Press, 2001. 145.

[10] Starr C, Morgan A G, Smith D B. J. Agric. Sci., 1981, 97: 107.

[11] Feng Y C, Hu C Q. J. Pharmaceut. Biomed., 2006, 41: 373.

[12] SUN Yu-qing(孙毓庆). Analytical Chemistry(分析化学). Beijing: People’s Medical Publishing House(北京： 人民卫生出版社), 1991. 10.

[13] Gujarati D N, Porter D C. Basic Econometrics(计量经济学基础). Translated by FEI Jian-ping(费剑平， 译). Beijing: China Renmin University Press(北京： 中国人民大学出版社), 2011. 75.

[14] Härdle W K, Simar L. Applied Multivariate Statistical Analysis. 2nd ed. Berlin: Springer-Verlag, 2007. 75.

[15] CHU Xiao-li(褚小立). Molecular Spectroscopy Analytical Technology Combined with Chemometrics and Its Applications(分子光谱与化学计量学及其应用). Beijing: Chemical Industry Press(北京： 化学工业出版社), 2011. 64.

[16] YAN Yan-lu, CHEN Bin, ZHU Da-zhou, et al(严衍禄， 陈 斌， 朱大洲， 等). Near Infrared Spectroscopy——Principles, Technologies and Applications(近红外光谱分析的原理、 技术与应用). Beijing: China Light Industry Press(北京： 中国轻工业出版社), 2013. 169.

*Corresponding author

Study on the Selection of Parameters for Evaluating Drug NIR Universal Quantitative Models

FENG Yan-chun, ZHANG Qi, HU Chang-qin*

National Institutes for Food and Drug Control, Beijing 100050, China

In order to find out the optimum combination of the evaluation parameters for the selection of the best drug near infrared (NIR) universal quantitative model during model optimization, 13 common evaluation parameters of NIR quantitative models were collected and arranged from commercial chemometrics software or references based on the requirements of validation of quantitative analytical procedures of ICH (International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use). Then all these parameters of 92 drug NIR universal quantitative models were calculated and analyzed. By studying the correlation of these parameters, the optimum combination of evaluation parameters for drug NIR universal quantitative models was determined. And the value range of these parameters in the optimum combination was also obtained. Root mean square error of cross-validation(RMSECV)/root mean square error of prediction (RMSEP), average relative deviation (ARD) and ratio of (standard error of) prediction (validation) to (standard) deviation (RPD) were used as the key parameters to evaluate the model accuracy. Most of RMSECV/RMSEP was within 3%, and the value of RMSECV was roughly equivalent to the average absolute deviation of the corresponding model. Most of RPD was more than 2. The value of ARD was related to the type of universal models (such as the drug preparation and packing) and the content range which the test sample belonged to. Determination coefficient (R2) was used as the key parameter to evaluate the model linearity and most of its values were from 80% to 100%. The ratio of RMSEP to RMSECV was selected as the key evaluation parameter of model robustness and its value was usually within 1.5. The standard deviation of repeated measurement data was chosen to evaluate model precision. And it was an important parameter for standardizing operation of NIR instruments and studying the feasibility of model transfer in different instruments. However, the parameter for NIR universal quantitative models

much less attention in previous studies and it was difficult to give a value range for this parameter at present. All the results can not only provide evidence for evaluation of drug NIR universal quantitative models for the model builders or users, but also supply basic data to establish and improve the parameter evaluation system of drug NIR universal quantitative models.

Drug; Near infrared spectroscopy; Universal quantitative models; Model optimization; Evaluation parameters; Accuracy; Linearity; Precision; Robustness

Oct. 1, 2015; accepted Feb. 5, 2016)

2015-10-01，

2016-02-05

国家公益性行业科研专项项目(2012104008)资助

冯艳春， 女， 1978年生， 中国食品药品检定研究院副研究员 e-mail： fyc@nifdc.org.cn *通讯联系人 e-mail： hucq@nifdc.org.cn

O657.3

A

10.3964/j.issn.1000-0593(2016)08-2447-08