微纳光纤环形腔海水温度的谐振光谱分析

杨红绢， 廖毅鹏， 王姗姗， 王 鑫， 王 晶

中国海洋大学信息科学与工程学院， 山东 青岛 266100

微纳光纤环形腔海水温度的谐振光谱分析

杨红绢， 廖毅鹏， 王姗姗， 王 鑫， 王 晶*

中国海洋大学信息科学与工程学院， 山东 青岛 266100

微纳光纤环形腔作为传感器件， 具有灵敏度高、 响应快的优点， 因而越来越广泛地应用在传感领域。 环形腔的谐振光谱直接反映外界环境的变化， 因此谐振光谱分析对探测环境参数至关重要。 从理论和实验研究了微纳光纤环形腔谐振光谱与海水温度的关系。 首先， 数值计算了基模(HE11)两个垂直偏振态的传播常数随光纤直径和探测波长的变化关系， 计算结果表明传播常数随光纤直径增大而增大， 随波长增大而减小， 同时计算了传播常数随海水温度的变化， 海水温度越高， 传播常数越大， 表明海水温度的变化会影响到模式的传播常数， 因而可以通过测量谐振光谱的变化得知海水温度的变化。 其次， 搭建了海水温度传感实验系统， 获得了微纳光纤环形腔海水温度的谐振光谱， 实验发现同时存在两套谐振峰， 分别对应基模的TE模和TM模， 两个偏振模式的传感灵敏度分别为5.54和5.24 pm·℃-1。 最后， 探讨了基模两个偏振态谐振光谱的产生原因， 由于结型耦合区的扭曲耦合使得两个偏振态分离， 并对两个偏振模式的谐振强度进行了分析。 两个模式的谐振强度不同， 而且随着波长的增加， 一个模的谐振强度不断增强， 另一个模的谐振强度逐渐减弱。 这是由于不同耦合态的耦合系数和衰减决定的， 而且他们随着波长而改变。 实验结果与理论计算相吻合。

谐振光谱； 海水温度； 微纳光纤环形腔； 传播常数； 偏振模式

引 言

微纳光纤由于倏逝场大、 传输损耗低等优点越来越受到关注， 由其制作的微结构器件也具有较大的研究价值， 包括传感器[1-3]、 激光器[4]、 滤波器[5]等。 基于微纳光纤环形腔的传感器取得了很大的研究进展， 具有尺寸小、 灵敏度高等特点， 已应用到折射率、 温度、 盐度、 湿度、 电流等物理量的传感探测[1, 6-9]。 环形腔的谐振深度可以达到20 dB， 自由光谱范围可以达到十几纳米， 品质因数高达106。 因此， 可以采用微纳光纤环形腔测量海水温度。

海水温度是海水的重要参数之一， 许多海洋现象的发生都伴随着海水温度的变化， 探测海水温度的变化具有良好的应用前景。 基于微纳光纤环形腔的海水温度传感。 首先， 从理论上分析了强度变化传感下灵敏度和探测极限随光纤直径、 环直径以及探测波长的变化关系， 对环形腔参数进行了优化[10]。 其次， 分别从理论和实验研究了谐振峰移传感方案下灵敏度随光纤直径和探测波长的变化关系， 进行了相关的实验， 通过优化传感器的参数， 灵敏度可以达到22.81 pm·℃-1[11]。 考虑到传感器的封装以及高灵敏度的需求， 从理论上研究了镀膜型微纳光纤环形腔传感器， 对镀膜方案进行了优化， 能够有效提高灵敏度[12]。 传感原理是利用谐振光谱的移动， 通过谐振波长的改变量反演海水温度的变化。 因此， 谐振光谱的细微结构对海水温度探测至关重要。

对微纳光纤及环形腔的结构进行了分析， 完成了海水温度传感实验， 发现谐振光谱存在两套谱线； 分析了两个偏振模式出现的原因， 并计算了两个偏振模式的传感灵敏度。 这为深入研究微纳光纤环形腔的谐振奠定了基础。

1 理论分析

1.1 微纳光纤环形腔及其谐振光谱特征参量

微纳光纤环形腔可以看做具有一面完美反射镜的FP谐振腔， 当光由输入端输入时， 可以分为两路光， 其中一路光经过环形腔与另一路光发生耦合， 产生谐振光谱。 微纳光纤环形腔的结构如图1所示。 根据耦合模理论和光纤传输理论， 输出与输入的光强比可以表示为[13]

(1)

其中，a是振幅衰减系数，K是耦合系数，σ=aexp(-αL)光传播一周后的损失的振幅，α是损耗，L是环形腔的周长，θ=βL是一周后的相位变化，β是模式的传播常数。

微纳光纤环形腔的谐振特性通过耦合模方程得到， 其谐振波长是[14]

(2)

其中neff=β/k是光波模式的有效折射率，L是环形腔的周长， 谐振光谱的自由光谱范围(FSR)就是相邻两个谐振波长之间的间隔， 可以近似表示为[14]

(3)

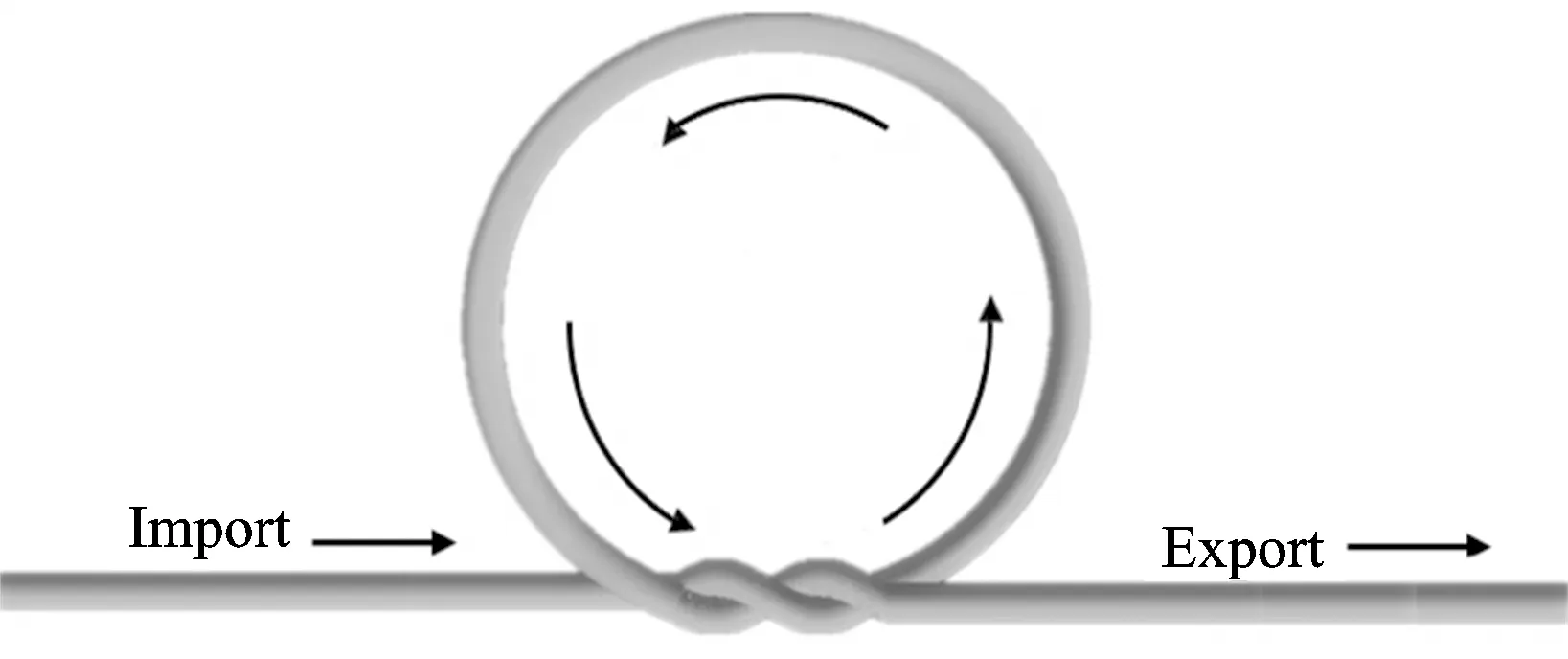
图1 微纳光纤环形腔结构示意图

1.2 微纳光纤的模式

图2(a)给出了一段微纳光纤， 该光纤具有圆对称的横截面，d为光纤直径。 将微纳光纤放置于海水中时， 其折射率剖面为阶跃折射率剖面， 如图2(b)所示，n1是氧化硅的折射率，n2是海水的折射率。 当光纤直径足够小的时候， 光纤中只有基模存在。 海水中微纳光纤的单模条件应该满足如下等式[15]

(4)

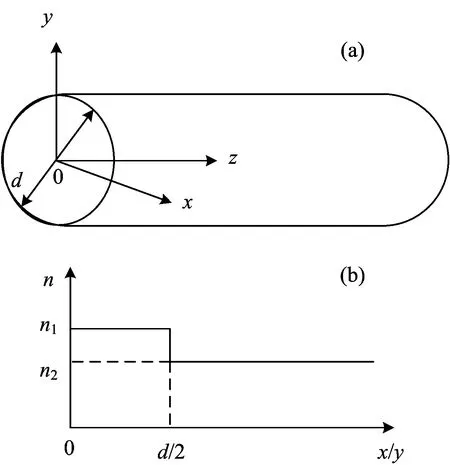
图2 (a)微纳光纤结构； (b)海水中微纳

n1可以由氧化硅折射率的色散公式中得出。 实验中所用的探测波长在红外波段， 而海水的折射率在这个波段没有数据， 因此我们用纯水的折射率近似代替海水的折射率。 当氧化硅折射率为1.45， 海水折射率为1.32， 探测波长选择为1 550 nm时， 计算得到此时的单模直径为1.98 μm。

考虑到偏振， 在圆形截面光纤中， 不存在优先的对称轴， 此时可以把横向电场的方向取处处平行于任意一对正交方向中的一个。 如图2(a)所示， 这一对正交方向记为x轴和y轴， 则在圆形光纤中存在基模的两个偏振态。 其中一个模式的横向电场与x轴平行， 另一个则与y轴平行。 圆形截面光纤的对称性使得这两个基模的标量传播常数(βx和βy)相等[15]。

对于基模(HE11)来说， 光波模式传播常数的标量解可以由以下公式通过数值方法得到[15-16]。

(5)

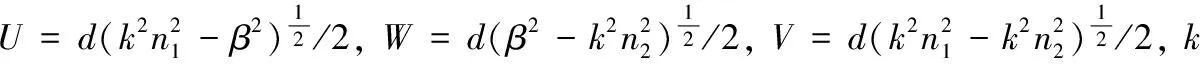
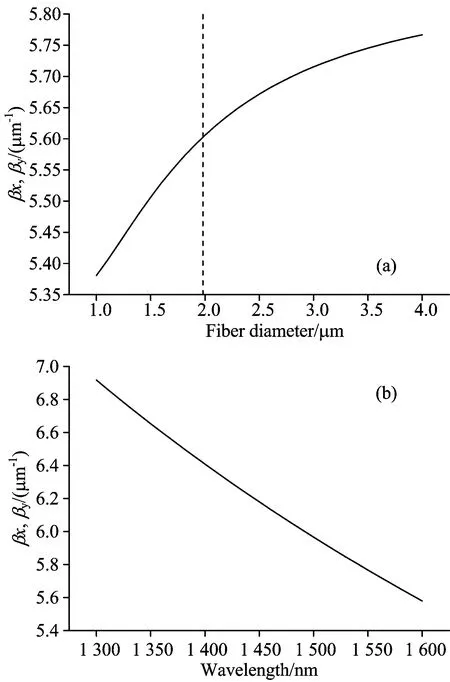
图3 基模的传播常数随光纤直径(a)和

Fig.3 The dependences of propagation constant of fundamental mode on fiber diameter (a) and probing wavelength (b)

数值计算了基模的传播常数随光纤直径和探测波长的变化， 如图3。 图3(a)中垂直于x轴的虚线表示的是单模直径的大小。 可见， 传播常数的大小与氧化硅和海水的折射率、 光纤直径以及波长相关， 传播常数随光纤直径增大而增大， 随波长增大而减小。 对于给定的实验样品， 外界环境温度的不同就会引起氧化硅和海水折射率的变化， 进而影响到传播常数。 这样就可以通过测量传播常数的变化测量外界环境温度的改变。 基模的传播常数与海水温度的变化关系如图4所示， 其中光纤直径为4 μm， 探测波长为1 550 nm。 可以看出， 随着温度的升高， 传播常数增大。 这是由于温度升高， 微纳光纤和海水的折射率都会发生改变， 进而引起传播常数的增大。 传播常数的改变会引起微纳光纤传感器输出光谱的变化， 因此通过研究光谱的变化可以得知海水温度改变的多少。

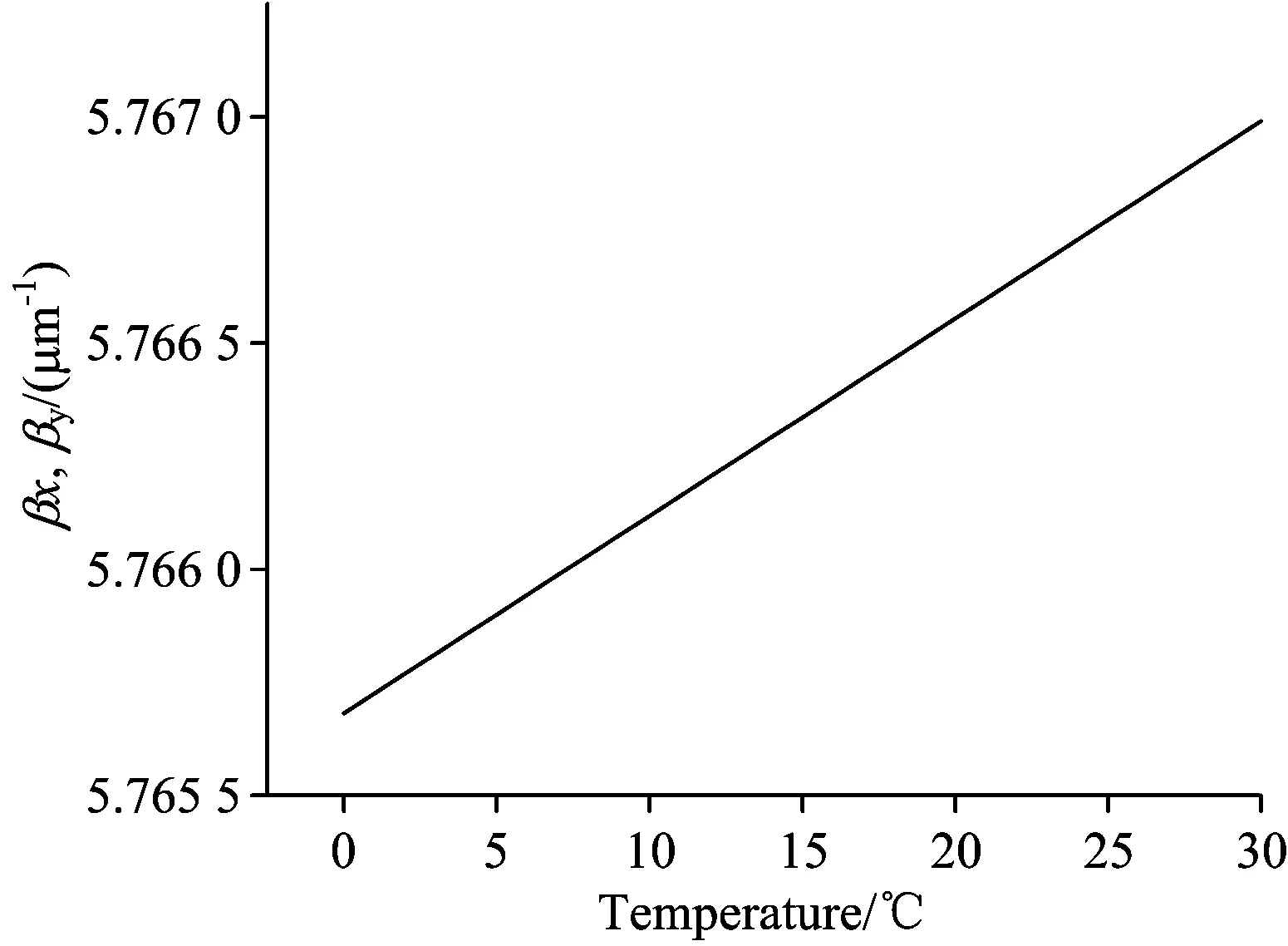
图4 基模传播常数与海水温度的变化关系

Fig.4 The dependences of propagation constant of fundamental mode on seawater temperature

2 结果与讨论

2.1 实验系统

整个实验的系统装置以及实验步骤参照文献[11]。 系统由超连续谱光源、 光谱分析仪、 恒温加热台、 热电偶温度计、 微纳光纤环形谐振腔和水槽组成。 超连续谱光源提供圆偏振宽带光， 光谱分析仪记录分析得到的光谱， 恒温加热台不断对海水加热提高海水的温度， 海水的温度从热电偶温度计中读出。

2.2 光谱测量及分析

实验中所拉制的微纳光纤环形腔直径为1 161 μm， 光纤直径为2.3 μm， 海水中环形腔的谐振光谱如图5所示。 可以明显的观察到两个模式的存在， 记为①模式和②模式。 两个模式的自由光谱范围FSR约为0.465 nm， 与理论计算得到的基模的FSR(0.47 nm)相近， 可以判断两个模式为基模的两个不同偏振状态(TE和TM偏振)。

不考虑TE和TM偏振态之间的耦合， 环形腔的传输强度可以写成两个偏振态传输强度的和， 即[17]

(6)

其中，W是环形腔的传输强度，A1和A2分别与TE或TM偏振的传输振幅有关。 不同的偏振态具有不同的耦合系数和衰减， 其传输振幅会有所不同。

当两个偏振态分离的时候， 环形腔的谐振光谱也会发生分离， 就会出现两套谐振光谱， 如图5所示。 谐振光谱的分离可以解释为结型耦合区的扭曲耦合， 这可以由偏振传输矩阵得到[18]。 从图中还可以观察到两个模式的谐振强度不同， 而且随着波长的增加， ①模的谐振强度不断增强， ②模的谐振强度逐渐减弱。 这是由于不同耦合态的耦合系数和衰减决定的， 而且他们随着波长的改变而有所不同。

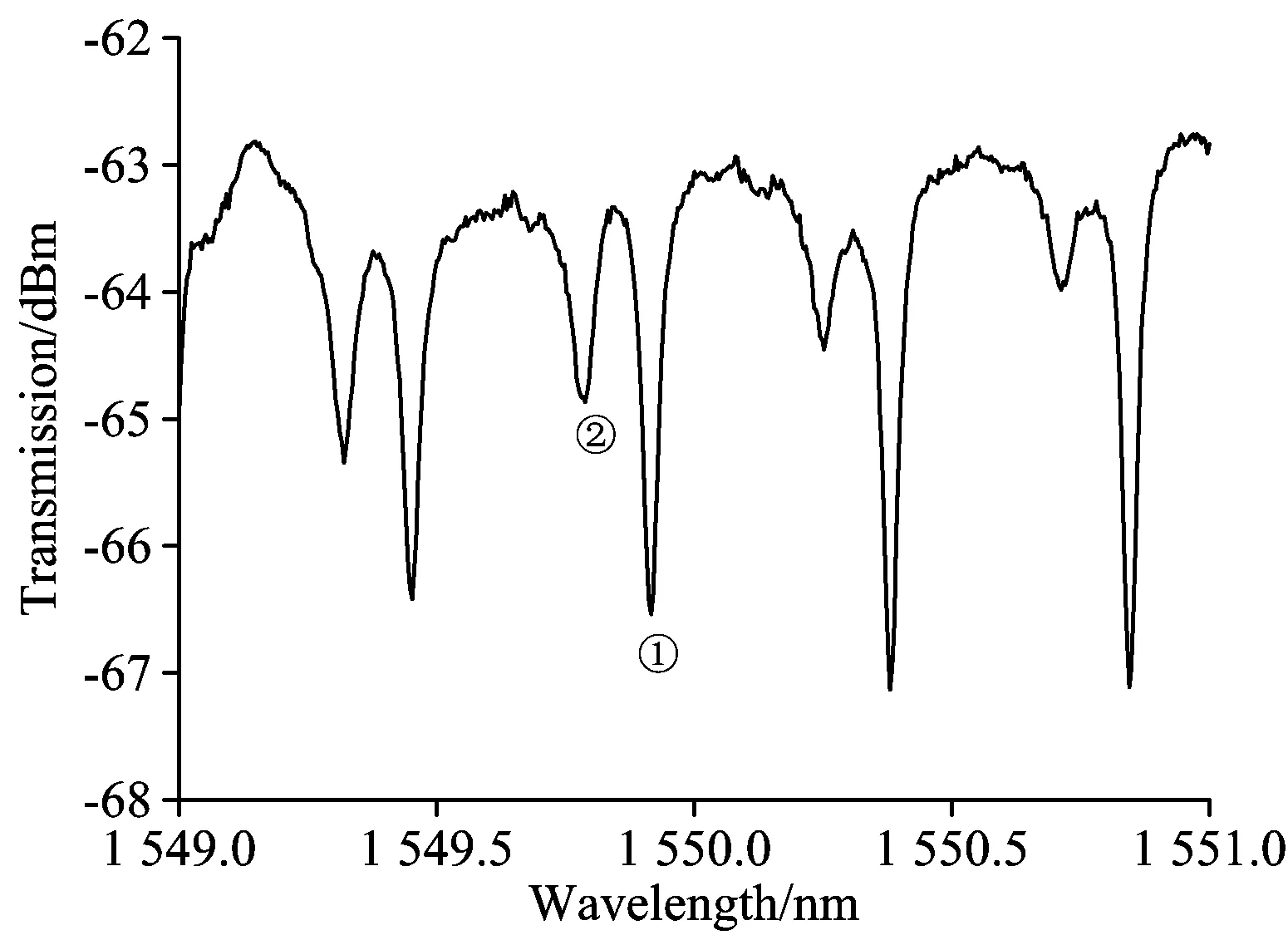
图5 微纳光纤环形腔的光谱图

2.3 海水温度传感

采用上述环形腔进行海水温度传感实验， 改变海水的温度， 测量不同温度下环形腔的谐振光谱， 得到的结果如图6(a)所示。 从图中可以看出， 两个模式的谐振波长， 都随着海水温度的增加向右移动。 分别绘制两个模式的谐振波长与温度的关系， 得到的结果如图6(b)所示。 两条拟合曲线的斜率

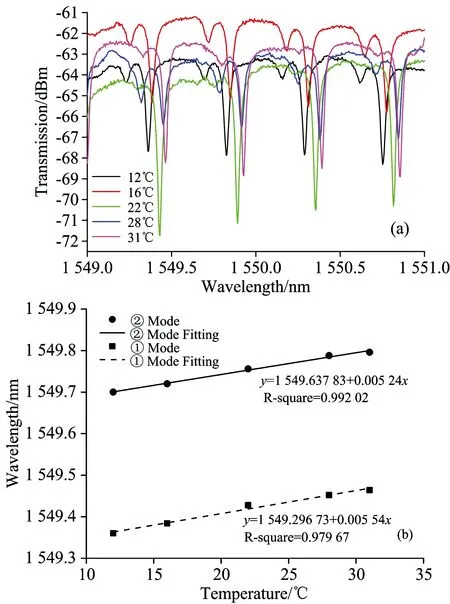
图6 (a)不同海水温度微纳光纤环形腔的谐振光谱；

Fig.6 (a) The spectra of the microfiber knot resonator in seawater at different temperatures； (b) The relationship between resonant wavelength and temperature for two polarization modes

分别为5.54和5.24 pm·℃-1。 也就是说， ①模的灵敏度为5.54 pm·℃-1， ②模的灵敏度为5.24 pm·℃-1， 两个模式的灵敏度相差很小。

3 结 论

研究了微纳光纤及环形腔的基模偏振态的谐振特性。 理论上研究了两个偏振态的基模传播常数随光纤直径和探测波长的变化关系， 实验上获得了微纳光纤环形谐振腔的谐振光谱， 并分析了两个偏振谐振光谱的产生原因。 结果表明， 两个基模的标量传播常数相同， 分别对应着TE模和TM模， 由于环形腔扭曲耦合的作用， TE模和TM模分离， 出现两套谐振谱， 两套谐振峰的传感灵敏度相差很小。 微纳光纤环形腔的谐振光谱分析解决了存在两套谐振光谱的难点， 为微纳光纤的光谱实验提供了指导。

[1] Guo X, Tong L M. Optics Express， 2008, 16(19): 14429.

[2] Li W, Hu Z F, Li X Y, et al. Optics Communications， 2014, 314: 28.

[3] Gu F X, Zeng H P, Tong L M, et al. Optics Letters， 2013, 38: 1826.

[4] Zhang Z S, Fan W, Gan J L, et al. Applied Physics Express， 2013, 6: 042702.

[5] Jung Y M, Brambilla G, Richardson D J. Optics Express， 2008, 16(19): 14661.

[6] Wang S S, Wang J, Li G X, et al. Applied Optics， 2012, 51(15): 3017.

[7] LI Guo-xiang, WANG Shan-shan, YANG Hong-juan, et al(李国祥， 王姗姗， 杨红绢， 等). Laser and Optoelectronics Progress(激光与光电子学进展)， 2014, 51: 050603.

[8] Li G X, Wang J, Yang H J, et al. The European Physical Journal Applied Physics, 2014, 68(2): 20502.

[9] WANG Xin, WANG Jing, WANG Shan-shan, et al(王 鑫， 王 晶， 王姗姗， 等). Acta Optica Sinica(光学学报)， 2014, 34, s206001.

[10] Yang H J, Wang J, Wang S S. Journal of the European Optical Society-Rapid Publications， 2014, 9: 14047.

[11] Yang H J, Wang S S, Wang X, et al. Sensors， 2014, 14(10): 18515.

[12] Yang H J, Wang S S, Mao K N, et al. Optics and Photonics Journal， 2014, 4: 91.

[13] Schwelb O. Journal of Lightwave Technology， 2004, 22(5): 1380.

[14] Chao C Y, Guo L J. Journal of Lightwave Technology， 2006, 24(3): 1395.

[15] Snyder A W, Love J D. Optical Waveguide Theory. New York: Chapman and Hall, 1991.

[16] Tong L M, Lou J Y, Mazur E. Optics Express， 2004, 12(6): 1025.

[17] Sumetsky M, Dulashko Y, Fini J M, et al. Journal of Lightwave Technology， 2006, 24(1): 242.

[18] Yu J H, Jin S S, Lu H H, et al. Numerical Simulation of Optoelectronic Devices (NUSOD), 2013. 13th International Conference on. IEEE, 2013: 121.

*Corresponding author

Analysis of Microfiber Knot Resonator Spectrum for Seawater Temperature

YANG Hong-juan, LIAO Yi-peng, WANG Shan-shan, WANG Xin, WANG Jing*

College of Information Science and Engineering, Ocean University of China, Qingdao 266100, China

As a sensing device, microfiber knot resonator (MKR) has been widely used in sensing field due to its advantages of high sensitivity and fast response. It is important to analyze the spectrum of MKR for detecting environmental parameters in that the spectrum can reflect the change of ambient environment. In this paper, the relationship between spectrum of MKR and seawater temperature has been studied theoretically and experimentally. Firstly, the dependences of the propagation constants of fundamental mode (HE11) on the fiber diameter and the probing wavelength are studied theoretically in this paper, including two orthogonal polarization states of fundamental mode. The calculated results show that the propagation constant increases with the increasing fiber diameter and the decreasing probing wavelength. Simultaneously, the dependence of propagation constant of fundamental mode on seawater temperature is studied. The results show that the larger propagation constant corresponds to the higher seawater temperature, which indicates that the seawater temperature affect the mode propagation constant. Thus, the seawater temperature can be obtained by detecting the resonant spectrum. Secondly, the experimental system for seawater temperature sensing is set up, with which the resonant spectrum of MKR for seawater temperature sensing are obtained. The experimental results show that two sets of resonant peak exist on the spectrum, which are corresponding to TE and TM modes of fundamental mode. The sensing sensitivities of the two polarization modes are 5.54 pm/°C and 5.24pm/°C, respectively. Finally, the reason for resonant spectrum of the two polarization states is discussed, which is that the separation of the two modes resulting from the twisted coupler of the knot zone, and the resonant intensity of the two polarization modes is analyzed. The resonant intensities of the two modes are different and one increases while the other one decreases with the increasing probing wavelength. It is determined by the coupling coefficients and attenuations of the two coupled states，which are affected by the probing wavelength. The experimental and theoretical results agree well.

Resonant spectrum; Seawater temperature; Microfiber knot resonator; Propagation constants; Polarization modes

Jan. 27, 2015; accepted May 6, 2015)

2015-01-27，

2015-05-06

国家自然科学基金项目(61171161)资助

杨红绢， 女， 1989年生， 中国海洋大学信息科学与工程学院博士研究生 e-mail： yanghongjuan123.hi@163.com *通讯联系人 e-mail： wjing@ouc.edu.cn

TN253

A

10.3964/j.issn.1000-0593(2016)08-2368-05