基于决策树模型的岩爆烈度预测

陈顺满，吴爱祥，王贻明，许梦国

( 1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京,100083;2.北京科技大学土木与环境工程学院，北京,100083；3.武汉科技大学资源与环境工程学院，湖北 武汉，430081)



基于决策树模型的岩爆烈度预测

陈顺满1，2，吴爱祥1，2，王贻明1，2，许梦国3

( 1.北京科技大学金属矿山高效开采与安全教育部重点实验室，北京,100083;2.北京科技大学土木与环境工程学院，北京,100083；3.武汉科技大学资源与环境工程学院，湖北 武汉，430081)

摘要：综合分析了岩爆的主要影响因素，选取岩石应力系数σθ/σc、岩石脆性系数σc/σt和弹性能量指数Wet作为评价指标，采用决策树方法进行岩爆烈度预测。以国内外比较典型的32个岩石地下工程实例作为基础样本数据，结合ID3算法建立了判定岩爆烈度的决策树模型。再选取15个工程实例，运用建立好的决策树模型对其岩爆烈度进行分级，并与实际岩爆等级以及采用模糊灰关联法、距离判别法、ν-SVR算法的评判结果进行对比。结果表明，本文提出的决策树方法具有计算简单、准确可靠、预测效率高的特点。

关键词：岩爆；烈度；决策树；预测；地下工程

岩爆是深埋地下工程施工过程中常见的动力破坏现象。当岩体中聚积的高弹性应变能大于岩石破坏所消耗的能量时，岩体结构平衡被破坏，多余的能量导致岩石爆裂，使岩石碎片从岩体中剥离、崩出。岩爆往往造成开挖工作面的严重破坏、设备损坏以及人员伤亡，带来巨大的经济损失和安全隐患。

目前，对岩爆的预测还没有形成比较统一的理论和技术，很多学者提出了各种假设和不同的理论判据，多种数学方法被应用到岩爆预测中，如模糊综合评判法[1]、分形插值法[2]、Bayes判别分析方法[3]和可拓工程方法[4]等，这些评判方法虽然取得了一定的应用效果，但也存在不足之处。例如，模糊综合评判方法对于相邻两类的差异难以区分，分形插值法受样本插值误差的影响较大，Bayes判别分析方法受样本数据的代表性和准确性的影响较大，可拓工程方法在计算关联度时容易遗漏一些约束条件。

由于岩爆的发生与多种影响因素相关，所以岩爆预测是一种高度非线性问题，目前对这种复杂的高度非线性问题没有可以利用的解析解。决策树方法是一种应用很广泛的归纳推理算法，它通过选取一系列无次序、无规则的实例样本作为基础数据，根据样本属性的不同对其进行归纳学习，进而形成自上而下的分类器和预测模型。本文在前人研究的基础上，选取影响岩爆的主要因素作为评价指标，以国内外大量工程实例为基础样本数据，运用决策树理论建立决策树预测模型，以期对岩爆烈度进行快速、高效的预测。

1岩爆烈度评价指标的选取

大量工程岩爆实例分析表明，岩爆常发生在高应力区的硬脆性岩石中。影响岩爆的因素分为两个方面：①由于高应力区新鲜岩体的开挖破坏了原岩应力环境，引起岩体周围的应力重新分布；②硬脆性岩石结构较致密、坚硬程度高，岩体中的弹性应变能突然释放，产生爆裂松动、剥落、弹射甚至抛射，从而引起岩爆。总的来看，围岩应力、岩性和岩体中的能量是影响岩爆的主要因素。

在分析围岩应力对岩爆的影响时，研究人员主要采用围岩最大切向应力σθ、围岩轴向应力σL、工程区最大地应力σ1、岩石单轴抗压强度σc和岩石单轴抗拉强度σt作为评价指标[5]；岩性对岩爆的影响主要运用陆家佑岩爆判别准则[6]进行评判；岩体中能量对岩爆的影响主要以弹性能量指数Wet作为评价指标。本文根据上述分析，采用应用效果较好且在工程中易于获取和对比的几个综合指标，即岩石应力系数σθ/σc、岩石脆性系数σc/σt和弹性能量指数Wet作为岩爆烈度的评判依据，具体指标的分级标准如表1所示[7]。

表1　岩爆烈度的评价指标和分级标准

2决策树的原理及算法

应用决策树方法需要构建树形模型，一旦形成了一棵完整的决策树，就可以在此基础上对未知对象进行分类和预测。决策树中的每一个分支都代表着一个测试输出，每个树叶节点代表类。对已经建立好的决策树，可以在数据库中形成一个系统，采用IF-THEN的语句形式，以提高决策树的分类效率[8-9]。

决策树算法很多，其中最为典型的是ID3算法，其他算法都是根据ID3算法演变而来的。ID3算法的目标是通过一系列测试将训练样本集划分为多个子集，其核心是在决策树中各级节点上选择属性，采用信息增益率作为属性选择的评判标准，使每个非叶子节点在进行测试时能获得被测试属性的最大类别信息[8-9]。

设E为选取的基础数据样本集合，整个属性集合具有n个不同的类别，所划分的等级属性记为Mi(i=1,2,…,n)。设Mi,E为集合E中的子集，即E中元组的集合，记|M|为整个集合的样本个数，|Mi,E|为Mi,E中的元素个数。对E中元组进行分类所得到的期望信息为：

(1)

式中：Info(E)为期望信息量，也称为E的熵；pi为集合E中任意子集属于等级Mi(i=1,2,…,n)的概率，pi=|Mi,E|/|M|。

设属性A具有n个不同的取值{V1,V2,…,Vn}，它可将E划分成v个子集{E1,E2,…,Ev}，假设Ej为某一等级的元组，那么属性A的信息熵为：

(2)

为了比较不同集合熵的大小，采用信息增益进行评判。信息增益表示原来的信息需求与新的信息需求之差，计算公式为：

Gain(A)=Info(E)-InfoA(E)

(3)

具有最大信息增益率的属性作为决策树的根节点，根据该根节点属性的取值划分出该节点的各个分支，同理划分出其他节点，依此建立最终的决策树模型。

3实例研究

3.1基础数据的选取

通过查阅大量的参考文献，选取国内外32个典型的工程实例[3,10-15]作为学习样本数据(见表2)建立决策树模型。

3.2决策树模型的建立

表2中的属性数据具有连续性，而决策树算法适合于处理离散的数据，因此可根据表1中的分级标准对表2中的数据进行离散化，部分结果如表3所示。

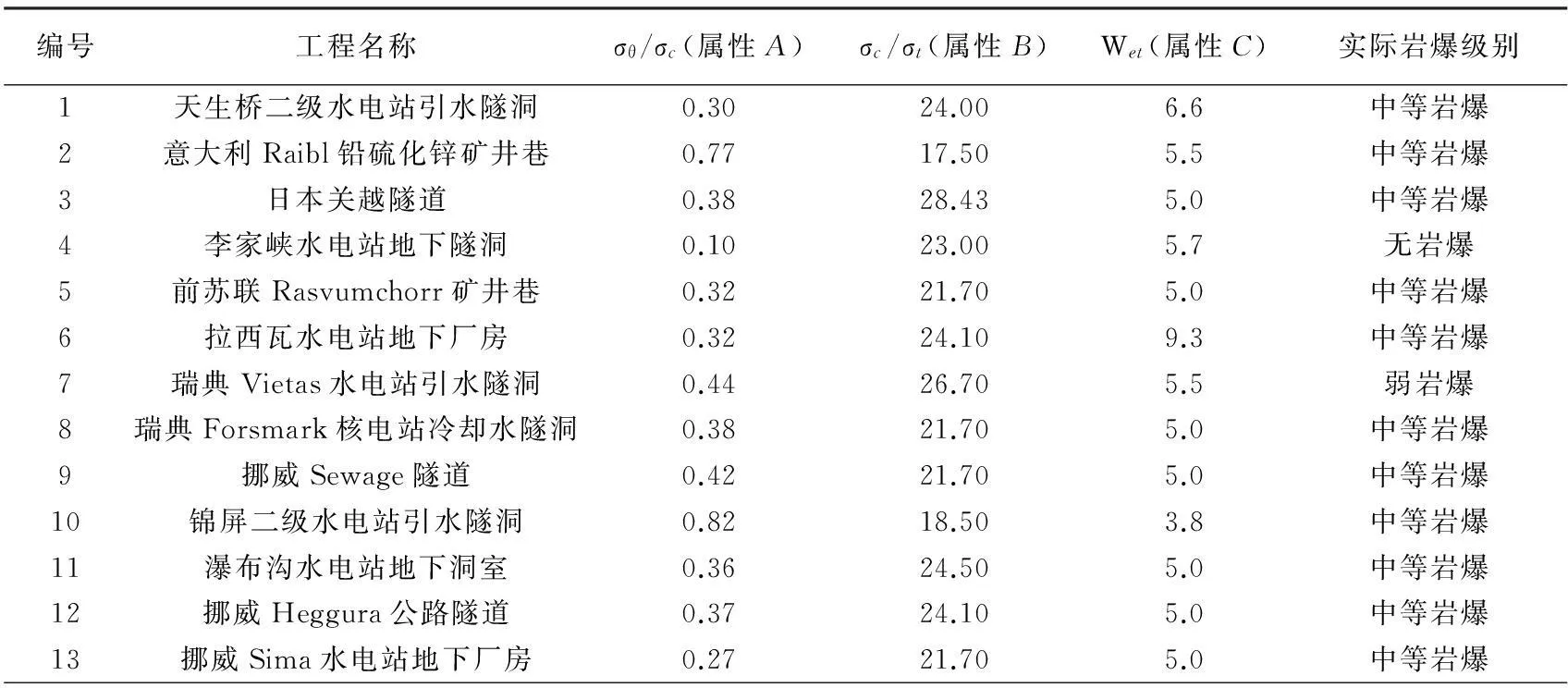
表2　决策树模型学习样本数据

续表

编号工程名称σθ/σc(属性A)σc/σt(属性B)Wet(属性C)实际岩爆级别14渔子溪水电站引水隧洞0.5314.809.0中等岩爆15鲁布革水电站地下隧洞0.2327.807.8无岩爆16龙羊峡水电站地下洞室0.1131.207.4无岩爆17二滩水电站2号支洞0.4129.707.3弱岩爆18秦岭隧道0.4314.007.4中等岩爆19秦岭隧道0.4015.007.1中等岩爆20秦岭隧道0.5515.006.4中等岩爆21冬瓜山深埋硬岩矿山岩体0.5511.104.0中等岩爆22通渝隧道0.5613.636.0弱岩爆23括苍山隧道岩体0.263.762.9弱岩爆24马路坪深埋硬岩矿山岩体0.7418.096.3强岩爆25马路坪深埋硬岩矿山岩体0.231.531.4无岩爆26马路坪深埋硬岩矿山岩体0.6114.645.1中等岩爆27马路坪深埋硬岩矿山岩体1.0011.242.0强岩爆28某深埋长隧道0.3114.902.5无岩爆29某深埋长隧道0.6216.003.0弱岩爆30某深埋长隧道0.8616.703.2中等岩爆31冬瓜山铜矿主矿体0.4514.823.1弱岩爆32冬瓜山铜矿主矿体0.2014.103.6无岩爆

表3　经过离散化的学习样本数据

根据式(1)可计算出样本的信息期望如下：

然后通过式(2)计算出各个属性的信息增益值。下面以属性A为例进行说明。

=0.9464

=1.1488

则属性A的信息熵为：

同理可以得到属性B和属性C的信息熵分别为：InfoB(E)=1.4093，InfoC(E)=1.3384。

通过式(3)可计算出各个属性的信息增益为：Gain(A)=0.6334，Gain(B)=0.2133，Gain(C)=0.2842。可以看出属性A具有最高的信息增益率，因此将属性A作为决策树模型的根节点，以此进行划分引出各个分支，样本的其他属性依此类推，从而建立起岩爆烈度等级划分的决策树模型，如图1所示。

3.3决策树模型的检验及结果分析

为了对预测岩爆烈度的决策树模型进行验证，本文从文献[16]中选取15个实际工程中的岩爆数据作为测试样本。这15个样本的基础数据和基于决策树的岩爆烈度分级结果见表4，为了对比分析，表4中还列出了采用模糊灰关联法[15]、距离判别法[12]、ν-SVR算法[16]的岩爆烈度分级结果。

从表4可以看出，本文建立的决策树模型对测试样本的评判准确率为86.7%，只有样本5和样本12的预测结果与实际情况有一定的差距。样本5和样本12的实际岩爆烈度均属于3级(弱岩爆)，而采用决策树模型对其进行评判的结果为2级(中等岩爆)，比实际岩爆烈度要高，从安全角度出发，这种误差是可以接受的。ν-SVR算法对测试样本的评判准确率也为86.7%，样本4和样本5的预测结果不准确，其中样本4的实际岩爆烈度为2级(中等岩爆)，但ν-SVR算法的判定结果为3级(弱岩爆)，从这点来看，决策树方法比ν-SVR算法更为合理，而且前者的计算速度更快。另外，采用模糊灰关联法和距离判别法对测试样本的评判准确率均为80%。综上所述，采用决策树模型对岩爆烈度进行预测是可行的，而且其具有准确率高、计算简便、预测效率高等优点。

图1　岩爆烈度预测决策树

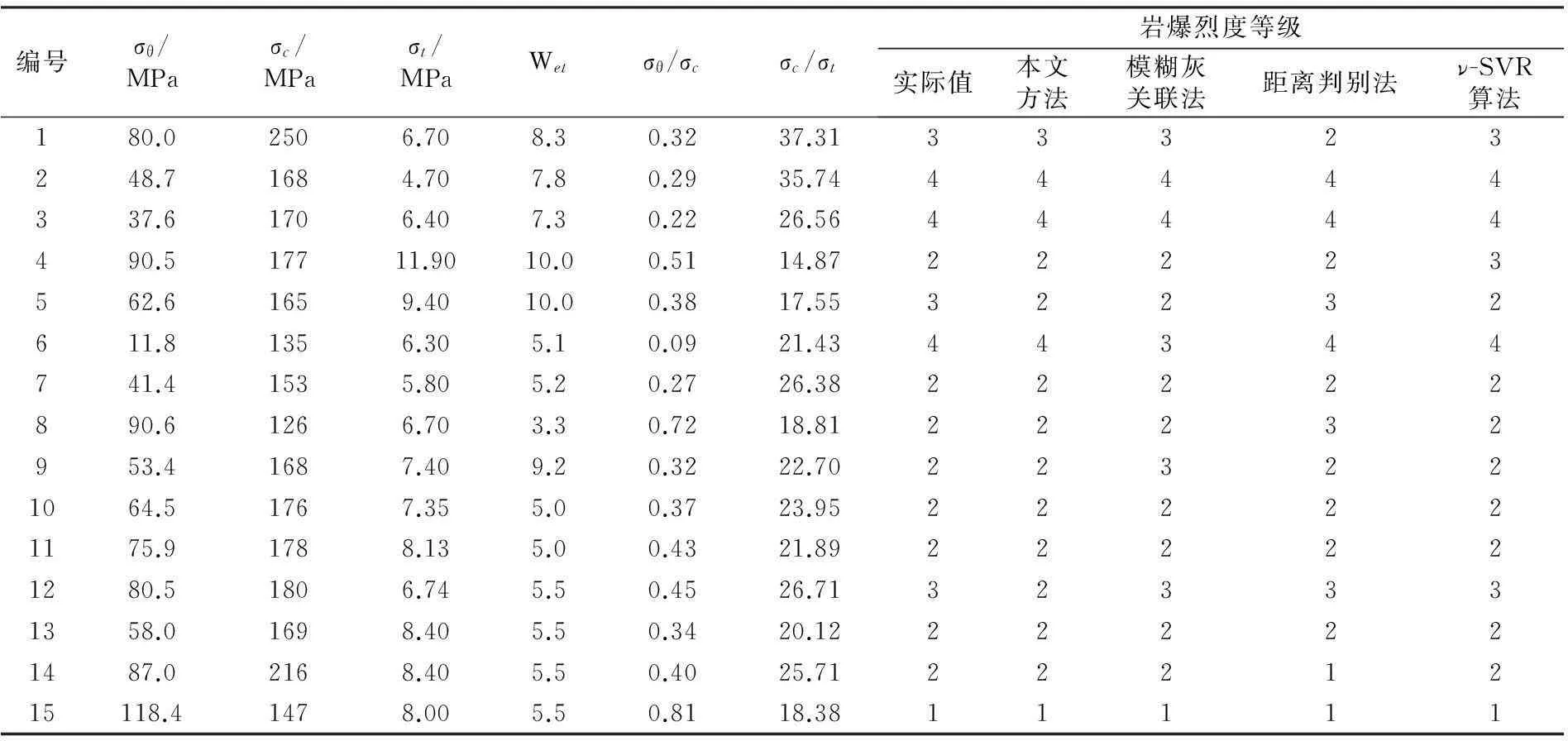
编号σθ/MPaσc/MPaσt/MPaWetσθ/σcσc/σt岩爆烈度等级实际值本文方法模糊灰关联法距离判别法ν-SVR算法180.02506.708.30.3237.3133323248.71684.707.80.2935.7444444337.61706.407.30.2226.5644444490.517711.9010.00.5114.8722223562.61659.4010.00.3817.5532232611.81356.305.10.0921.4344344741.41535.805.20.2726.3822222890.61266.703.30.7218.8122232953.41687.409.20.3222.70223221064.51767.355.00.3723.95222221175.91788.135.00.4321.89222221280.51806.745.50.4526.71323331358.01698.405.50.3420.12222221487.02168.405.50.4025.712221215118.41478.005.50.8118.3811111

4结语

本文选择能准确反映岩石的基本特征且通过试验容易获取的岩石应力系数σθ/σc、岩石脆性系数σc/σt和弹性能量指数Wet作为岩爆烈度预测指标。采用众多的岩爆工程实例建立了用于岩爆预测的决策树模型，并通过工程实例进行模型检验，结果显示岩爆烈度评判准确率达到86.7%，且误判的岩爆烈度等级比实际岩爆烈度等级略高，从安全角度考虑，这对工程施工中采取积极防御措施是有利的。决策树方法具有准确率高、计算简便、效率高等优点，为工程实际中进行岩爆烈度预测提供了一种新的手段。

参考文献

[1]王元汉，李卧东，李启光，等．岩爆预测的模糊数学综合评判方法[J]．岩石力学与工程学报，1998，17(5)：493-501．

[2]田杰，王威，郭小东，等．基于分形插值模型的岩爆预测研究[J]．北京工业大学学报，2012，38(4)：481-487．

[3]宫凤强，李夕兵，张伟．基于Bayes判别分析方法的地下工程岩爆发生及烈度分级预测[J]．岩土力学，2010，31(S1)：370-377，387．

[4]熊孝波，桂国庆，许建聪，等．可拓工程方法在地下工程岩爆预测中的应用[J]．解放军理工大学学报：自然科学版，2007，8(6)：695-701．

[5]陈海军，郦能惠，聂德新，等．岩爆预测的人工神经网络模型[J]．岩土工程学报，2002，24(2)：229-232．

[6]陆家佑．岩爆数值模拟与预测[C]//第三届全国岩石动力学学术会议论文选集.武汉：武汉测绘科技大学出版社，1992：451-462.

[7]杨莹春，诸静．一种新的岩爆分级预报模型及其应用[J]．煤炭学报，2000，25(2)：169-172.

[8]高德，李晓．决策树在岩体质量分级中的应用[J]．西北大学学报：自然科学版，2011，41(S)：265-269．

[9]魏晓云．决策树分类方法研究[J]．计算机系统应用，2007(9)：42-45．

[10]刘金海，冯涛，袁坚．基于非线性灰色归类模型的岩爆预测方法[J]．地下空间与工程学报，2005，1(6)：821-824．

[11]赵国彦，刘强，刘超．岩爆烈度分级预测中的贝叶斯判别分析[J]．金属矿山，2010(5)：143-147．

[12]宫凤强，李夕兵．岩爆发生和烈度分级预测的距离判别方法及应用[J]．岩石力学与工程学报，2007，26(5)：1012-1018．

[13]杨金林，李夕兵，周子龙，等．基于粗糙集理论的岩爆预测模糊综合评价[J]．金属矿山，2010(6)：26-29．

[14]陈秀铜，李璐．基于AHP-FUZZY方法的隧道岩爆预测[J]．煤炭学报，2008，33(11)：1230-1234．

[15]王发芝，汪令辉，谢学斌．模糊灰关联模式识别方法在岩爆预测中的应用[J]．金属矿山，2009(5)：172-174．

[16]祝云华，刘新荣，周军平．基于ν-SVR算法的岩爆预测分析[J]．煤炭学报，2008，33(3)：277-281．

[责任编辑尚晶]

Prediction of rockburst intensity based on decision tree model

ChenShunman1,2，WuAixiang1,2，WangYiming1,2，XuMengguo3

( 1. Key Laboratory of High-efficiency Mining and Safety of Metal Mines of Ministry of Education, University ofScience and Technology Beijing, Beijing 100083, China; 2. School of Civil and Environmental Engineering,University of Science and Technology Beijing, Beijing 100083，China; 3. College of Resources and EnvironmentalEngineering, Wuhan University of Science and Technology, Wuhan 430081, China)

Abstract:On the basis of analyzing the major influencing factors in rockburst, decision tree method is applied to predict the rockburst intensity with rock stress coefficient σθ/σc, rock brittleness coefficient σc/σt and elastic energy index Wetas evaluation indicators. Thirty-two typical domestic and overseas underground rock projects are chosen as the basic sample data, and the decision tree model is built using ID3 algorithm. Rockburst intensities of another fifteen projects are graded by this model. The results are compared with the actual rockburst grades as well as the evaluation results by fuzzy grey incidence theory, distance discriminant analysis and ν-SVR algorithm, which indicates that the proposed decision tree method is simple and reliable, and has higher accuracy and efficiency.

Key words：rockburst; intensity; decision tree; prediction; underground engineering

收稿日期：2016-01-22

基金项目：“十二五”国家科技支撑计划项目(2012BAB08B02)；教育部长江学者和创新团队发展计划项目(IRT0950).

作者简介：陈顺满(1989-)，男，北京科技大学博士生.E-mail：shunman_chen1989@sina.cn通讯作者：吴爱祥(1963-)，男，北京科技大学教授，博士生导师.E-mail：wuaixiang@126.com

中图分类号：TD32；TU452

文献标志码：A

文章编号：1674-3644(2016)03-0195-05