精确延时对台阶爆破岩石破碎块度影响的数值模拟研究❋
2016-06-14李顺波杨仁树杨
李顺波杨仁树杨 军
①中国矿业大学(北京)力学与建筑工程学院(北京,100083)②北京理工大学爆炸科学与技术国家重点实验室(北京,100081)
精确延时对台阶爆破岩石破碎块度影响的数值模拟研究❋
李顺波①杨仁树①杨 军②
①中国矿业大学(北京)力学与建筑工程学院(北京,100083)
②北京理工大学爆炸科学与技术国家重点实验室(北京,100081)
[摘 要]为了研究精确延时间隔对岩石破碎的影响,利用有限元软件就不同延时间隔条件对岩石破碎的影响进行了数值模拟研究。研究结果表明:合理设定延时间隔利于台阶顶部岩石破碎块度控制,同时能够改善岩石破碎块度分布情况。通过爆生气体和应力波关系的分析,计算得出的延时间隔和数值模拟结果较为接近;在本次数值模拟中,延时间隔6 ms、抵抗线3 m,即延时间隔和抵抗线关系为2 ms/ m情况下有利于岩石破碎。
[关键词]岩石破碎;精确延时;数值模拟
[分类号] TD853
引言
随着数码电子雷管的诞生和使用,毫秒延时间隔对爆破效果的影响越来越受到人们的重视,特别是在爆破振动控制和岩石破碎这两个方面。数码电子雷管具有延时精度高、延时间隔在1~1000 ms范围内随意设定的优点,使得通过改变毫秒延时间隔来控制岩石破碎块度成为了一种可能。
国内外很多学者在这一方面进行了大量的尝试,Stagg等[1]通过试验得到了毫秒延时间隔3.3 ms/m时利于岩石的破碎;Otterness等[2]通过大量的实践得出毫秒延时间隔3.3~13.0ms/m时可以使得大块率降低12%~20%;张乐等[3]通过对隆芯1号数码电子雷管在德兴铜矿工业试验中的爆破振动监测,发现应用数码电子雷管可以改善矿岩的破碎度,提高综合经济效益。
Paley等[4]在美国Red Dog Mine中,采用精确延时电子雷管将延时间隔25 ms缩短到17 ms;在普通雷管的情况下,将岩石大块率增加20%;若采用电子雷管,大块率则降低30%,这样能很好地改善岩石破碎效果。Koenig[5]利用精确延时电子雷管,将块度小于500 mm的岩石由原来的57%增加到79%,同时块度大于1 000 mm的岩石由27%减少至5%。Lewis[6]、McKinstry[7]等通过研究发现,利用精确延时电子雷管可以取得良好的破碎效果。Batten等[8]在Newlands煤矿中利用电子雷管改善剥离岩体质量,提高了生产效率,取得了良好的经济效果。Petropoulos等[9]通过室内的模型试验,探讨了不同延时间隔对岩石破碎的影响。Schill[10]通过LS-DYNA软件模拟了不同毫秒延时间隔情况下岩石破碎形态。
以上分析可以看出,精确延时间隔对岩石破碎效果的改善已经受到越来越多学者的关注,同时通过相关试验和现场实践,进一步验证了精确延时在岩石块度改善方面具有优势。但是,目前对于毫秒延时对岩石破碎影响的机理和毫秒延时间隔设定都是不明确的。因此,本文从数值模拟角度出发,进一步直观地揭示毫秒延时间隔和岩石破碎之间的本质联系。
1 理论分析
炸药在岩体爆炸时产生冲击波,后续产生应力波并向远处传播,其在时间和空间上的发展形态如图1中所示[11]。其中,“+”表示压缩波;“-”表示拉伸波;ΛW表示波长;τW表示波传播ΛW所需的时间;σ为应力;t为时间;X为距离。
采用一维拉格朗日描述应力波在时间和空间上的关系,如图2所示。其中,SE为S波(横波)拉伸波;SF为S波压缩波;PE为P波(纵波)拉伸波;PF为P波压缩波。由于P波和S波传播速度的不同,因此,在同一距离处二者已经发生了分离。从图2中看出了P波和S波相互作用的区域的形成。
进一步考察应力波之间的相互作用,两孔产生的应力波的一维拉格朗日表示方法见图3。1#、2#为炮孔1#和炮孔2#。
图3中可以看出S波和P波在拉伸波和压缩波之间形成的不同作用区域。若二者之间存在延时间隔,孔2#产生的压缩波和拉伸波将沿坐标轴纵轴向上移动,形成新的作用区域范围,如图3(b)中所示。在t∗时刻X∗处的O∗点位于图3(a)中,受到孔1#产生的S波压缩波、孔2#产生的P波压缩波的作用;同样,在图3(b)中,O∗点受到孔1#产生的S波压缩波和孔2#产生的S波拉伸波的作用。在同时起爆情况下,O∗点受到压缩波的作用;在具有延时间隔情况下,受到压缩波和拉伸波的作用,因此延时间隔的存在,能够改变某一点的受力状态,从而能够改变岩石的破碎效果。
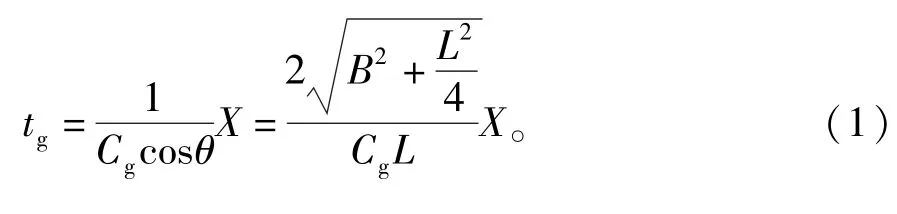
其中:tg为爆生气体到达A点所需的时间;Cg爆生气体传播速度;B为抵抗线;L为孔间距。

其中:Cp为纵波波速;Δt为延时间隔。
假设孔1#产生的爆生气体和孔2#产生的应力波在A点相遇,在X=L/4时[12]取的极值,此时Δt可以表示为:
2 数值模拟
2. 1 数值模拟模型
数码电子雷管在实现精确延时控制的同时,也实现了逐孔起爆。因此,数值模拟中主要探讨相邻两个炮孔由于延时间隔的改变造成的影响。由于受到计算机计算能力限制,建立如图5所示的小型数值模拟计算模型。模型高度为15. 0 m,炮孔直径为200 mm,台阶顶部宽度为10. 0 m,台阶底部宽度为17. 5 m,台阶高度为10. 0 m,台阶长18. 0 m,装药高度7. 0 m,填塞长度为3. 0 m,两孔间距为6. 0 m,抵抗线为3. 0 m,台阶顶部和前部为自由边界,其他面施加无反射边界。设定延时间隔分别为0、2、4、6、8 ms 5种情况。
2. 2 数值模拟材料模型和参数
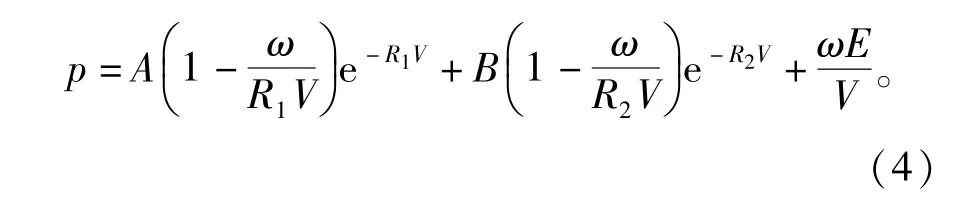

表1 炸药状态参数Tab. 1 Status parameters of the explosive
岩石和填塞材料用RHT模型进行描述,其强度模型是通过引入3个极限面来实现:初始的弹性屈服面、失效面以及残余强度面。
主要材料参数见表2。其中:G为Gruneisen常数;B0、B1、T1、T2为状态方程参数;A1、A2、A3为Hagoniot方程参数;A、N为屈服面参数;Q0、B为Lode角参数;Gc为压缩屈服面参数;GT为拉伸屈服面参数;XI为剪切模量折减系数;D1、D2为损伤因子;AF、NF为剩余面参数。
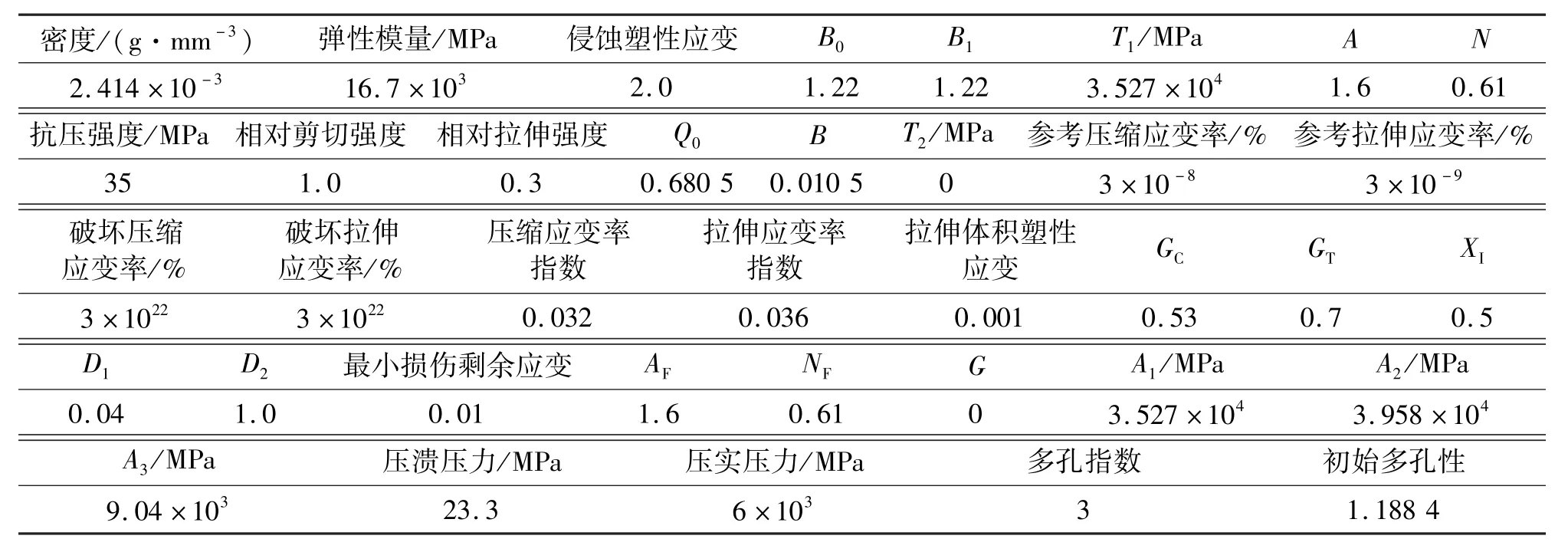
表2 岩石材料参数Tab. 2 Parameters of rocks
3个曲面解释了沿着不同的子午线强度的降低,同时也解释了应变率效应。失效面,也就是岩石最终强度,是由不同的材料参数组成,其中包括岩石的压缩、拉伸、剪切强度。初始屈服面是有的用户所输入的一部分数据(沿着拉伸和压缩子午线的失效面)加上另一段曲线(使整个曲线在孔隙压溃压力值处封闭)组成。典型的加载状况,见图6。
模型在达到初始屈服面之前为弹性,超过后认为有塑性应变出现。通过初始屈服面和失效面的差值的方法,把结合了岩石硬化特性的塑性应变用于形成有效屈服面。同样,当应力达到失效面时,加入参数化的损伤模型来控制损伤演化,这个损伤演化也是由塑性应变驱动的。通过失效面和剩余强度面的差值,损伤演化继而表现了失效应力后的极限面。对于完全损伤材料,没有子午线或者应变率关系,剪切强度只是在限制条件(即正压力的情况下)下才存在。
2. 3 数值模拟结果
图7中的整个台阶的破碎形态图中,在不同延时间隔情况下,炮孔周围的破碎形态呈现不同的变化范围,特别是在右侧炮孔的根部和顶部的变化形态显著地不同。在两孔中间的台阶坡面位置上,图7(d)中形成了两条接近连接的破碎裂纹,有助于岩石破碎形态的分割。其他几种延时间隔情况下,只有在上部形成一条破碎裂纹,并形成多个“孤岛区域”,这就容易造成岩石块度的不均匀,不利于整个岩石块度分布形态。右侧炮孔的底部(右下角)形成的延伸裂纹区域,在2 ms和6 ms情况下较长;同时在8 ms情况下,右侧炮孔底部形成一个对称区域,可以看出不同的延时间隔对于整个炮孔区域的发展具有重要的影响。
图8给出了两炮孔连线中点处切面的损伤变化情况,将损伤值大于0. 7的区域进行删除后形成图8中的区域范围。
从图8中可以看出,随着延时间隔的增大,在台阶上部范围内的预留面积存在先减小而后增大的过程,延时间隔0 ms时刻的上部面积最大,6 ms时刻的上部面积最小。在台阶中部范围内,延时间隔2 ms时刻在后部和前部都形成较大的预留区域,其他情况只是在前部范围内出现较大的预留区域。延时间隔4 ms和6 ms两种情况下,在台阶中部的后部位置的预留区域的面积变化较为均匀;在台阶的中后部位置,延时间隔0 ms时刻的预留区域面积较小[图8(a)中圆圈位置],存在一些过度破碎的情况。在台阶的底部,随着延时间隔的增大,根底的变化存在较小的差异。
为了更直观地考察延时间隔对岩石破碎的影响,将图8的预留区域的面积进行了统计,两炮孔中点切面剩余的面积如图9所示。
从图9可以看出,延时间隔0 ms时刻的预留面积最小,延时间隔4 ms时刻的预留面积最大,延时间隔2 ms时的预留面积次之,延时间隔6 ms和8 ms时的预留面积差别不是很大。在图9中,预留面积最小值与最大值相差10%。从而可以看出,合理的毫秒延时间隔可以较好地改善岩石破碎情况,同时大幅降低岩石的破碎块度比例范围,对于台阶上部的岩石破碎情况有一定的改善作用,从而降低大块的产生。根据文献[12]给出的爆生气体速度Cg=300 m/ s,Cp=4 000 m/ s,利用公式(3)计算出延时间隔约为5. 77 ms,这和数值模拟在6 ms的情况较为吻合。
图10给出了两孔顶部连线中点处(图5中E点)的损伤值随着时间变化关系。从图10可以看出,具有延时间隔的情况下,随着两孔间的延时间隔增加,损伤值变化在前期较为一致;同时,4 ms和6 ms两种情况的损伤变化曲线出现了重叠,说明二者的损伤值随着时间的变化差别较小。
3 结论
利用一维拉格朗日波形理论,直观地揭示了延时间隔能够改变岩石中某点的受力状态,并通过对不同延时间隔情况下的台阶爆破进行数值模拟,进一步明确了延时间隔对于岩石破碎具有较大的影响。合理设置延时间隔对改善台阶上部岩石破碎情况具有重要的影响,同时可以避免岩石过度破碎,进一步优化岩石破碎块度比例范围。
对在文中所采用参数的情况下的数值模拟结果进行分析,同时,通过爆生气体和应力波关系计算出的延时间隔和数值模拟得出的结果较为接近,有利于岩石破碎的延时间隔为6 ms,其与抵抗线的关系为2 ms/ m。
参考文献
[1] STAGG M S,RHOLL S A. Effects of accurate delays on fragmentation for single-row blasting in a 6. 7 m(22 ft)bench[C]/ / Fragblast 2. Proceedings of the 2nd International Symposium on Rock Fragmentation by Blasting. SEM,Bethel CT,1987:210-230.
[2] OTTERNESS R E,STAGG M S,RHOLL S A. Correla-tion of shock design parameters to fragmentation[C]/ / Proceedings of the 7th ISEE Conference on Explosives and Blasting Research. Las Vegas,Nevada,1991:179-181.
[3] 张乐,颜景龙,李风国,等.隆芯1号数码电子雷管在露天采矿中的应用[J].工程爆破,2010,16(4):73-77. ZHANG L,YAN J L,LI F G,et al. Application of Lux No. 1 digital electronic detonator in an open pit mine[J]. Engineering Blasting,2010,16(4):73-77.
[4] PALEY N,ALASKA T. Testing electronic detonators to increase SAG mill through put at the Red Dog Mine [C]/ / Proceeding of the 36th Annual Conference on Explosives and Blasting Technique. San Diego,California,2010:302-315.
[5] KOENIG R. Five years experience with the dynatronic electronic firing system[C]/ / Proceedings of the 24th Annual Conference on Explosives and Blasting Technique. New Orleans,1998:359-364.
[6] LEWIS N,PEREIRA P. Operating improvements at vulcan materials mccook quarry using electronic detonators[C]/ / Proceedings of the 29th Annual Conference on Explosives and Blasting Technique. Nashville,2003:1-14.
[7] MCKINSTRY R,FLOYD J,BARTLEY D. Electronic detonator performance evaluation[C]/ / Proceedings of the 28th Annual Conference on Explosives and Blasting Technique. Las Vegas,2002:1-20.
[8] BATTEN C,WILLAN L,SPARKES M. Productive partnership-advanced blasting technology at Newlands Coal Mine[C]/ / Proceedings of the 37th Annual Conference on Explosives and Blasting Technique. San Diego,California,2010:120-132.
[9] PETROPOULOS N,JOHANSSON D,OUCHTERLONY F. Fragmentation under different confinement conditions and the burden behavior—small scale tests[M]/ / BLANCO J A S,SINGH A K. Measurement and Analysis of Blast Fragmentation. Boca Raton,FL:CRC Press,2012:61.
[10] SCHILL M. Finite element simulations of blasting and the effects of precise initiation on fragmentation[R]. DYNA more report,2011.
[11] ROSSMANITH H P. The use of lagrange diagrams in precise initiation blasting. Part I:two interacting blastholes[J]. Fragblast:International Journal for Blasting and Fragmentation,2002,6(1):104-136.
[12] CHO S H,KANEKO K. Rock fragmentation control in blasting[J]. Materials Transactions,2004,4(5):1722-1730
Numerical Simulation of the Impact of Precise Time Delay on Rock Fragmentation in Bench Blasting
LI Shunbo①,YANG Renshu①,YANG Jun②
①School of Mechanic & Civil Engineering,China University of Mining & Technology(Beijing)(Beijing,100083)
②State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology(Beijing,100081)
[ABSTRACT] In order to study effects of the precise time delay interval on rock fragmentation,the finite element software was used to simulate the rock fragmentation under different time delay intervals. The results show that the reasonable delay time setting is advantageous to control the rock fragmentation on top,and can improve the fragmentation distribution of rock. Through the analysis of the relationship between stress wave and detonation gas,it is found that the results of delay interval time is close to those of numerical simulation. The delay time interval is 6 ms,and the resistance line is 3 m. And when the relationship between delay time interval and resistance is 2 ms/ m,it is conducive to the rock fragmentation under this numerical simulation.
[KEY WORDS] rock fragmentation;precise time delay;numerical simulation
doi:10. 3969/ j. issn. 1001-8352. 2016. 03. 003
收稿日期:❋2015-10-27
作者简介:李顺波(1985-),男,博士,中国矿业大学(北京)博士后流动站从事岩石爆破理论方面的工作。E-mail:lshunbo@126. com
