水驱开发多层油藏井间连通性反演模型
2016-06-13赵辉康志江孙海涛张贤松李颖长江大学石油工程学院中国石油化工股份有限公司石油勘探开发研究院海洋石油高效开发国家重点实验室
赵辉,康志江,孙海涛,张贤松,李颖(. 长江大学石油工程学院;. 中国石油化工股份有限公司石油勘探开发研究院;. 海洋石油高效开发国家重点实验室)
水驱开发多层油藏井间连通性反演模型
赵辉1,康志江2,孙海涛1,张贤松3,李颖1
(1. 长江大学石油工程学院;2. 中国石油化工股份有限公司石油勘探开发研究院;3. 海洋石油高效开发国家重点实验室)
摘要:针对当前井间连通性模型只能预测产液动态变化、无法计算油水两相动态且不能分层进行连通性分析等局限性,建立了新的可模拟油水动态的多层油藏井间连通性模型。模型将油藏系统分层离散成一系列由井间传导率和连通体积等参数表征的井间连通单元,并以连通单元为模拟对象进行物质平衡方程计算,通过考虑定液、定压两种生产模式实现压力求解和井间流量计算,结合前缘推进理论建立了井间饱和度追踪计算方法,最终得出井点处各层的油水产出动态;以此为基础利用随机扰动近似法和投影梯度法等通过动态拟合建立了模型参数反演方法。实例应用显示,所建模型取得了较好的动态拟合和预测效果,反演后的连通模型参数与实际油藏地质特征相吻合,验证了方法的正确性;相比当前连通性方法,模型能实时获得分层井间流量分配系数、单井产液和产油劈分系数等信息,可以更准确地反映油藏平面及纵向的油水流动关系和生产措施变化,指导油田实际生产。图8参28
关键词:多层油藏;井间连通性;反演模型;井间连通单元;井间流量分配系数;油井产量劈分系数
0 引言
油层井间连通性评价是油藏注水开发设计的基础,对于优化注采结构关系、分析剩余油分布规律和制定加密调剖等措施方案具有重要的指导作用[1-3]。实际矿场一般通过示踪剂测试、井间微地震、干扰试井等方法来认识井间连通性[4-5],但其存在影响实际生产、解释周期长、费用高等缺点,无法满足区块和油田整体认识的需要。
利用油田注采数据研究井间连通性是另一类非常重要的方法,其具有操作简单、计算快速、反演范围大等特点,其反演模型主要包括相关分析模型[6]、多元回归模型[7]、电容模型[8-15]和系统分析模型[16]等。前两种模型通过拟合实际产液数据获取注采动态的相关系数来表征井间连通状况。后两种模型实质是对多元回归模型中的注入速度进行滤波校正,使其能够考虑注入动态的时滞特性,更符合油藏实际渗流特点。其中,电容模型是基于水电相似和物质平衡原理得出的注入速度时滞模型[11-15],而系统分析模型基于注采系统的一阶时滞特性而建立[16]。
上述连通性模型虽然能在不同程度上获取井间连通性的信息,但主要存在以下问题:模型较为理想和简化、考虑因素较少,不能分层进行连通性分析计算,难以表征层间的非均质特性;模型反演的连通性参数缺乏明确的地质意义;不能考虑关停井及油井转注等状况,反演结果受措施调整影响较大;仅能对产液数据进行预测拟合,不能综合其他油水动态指标如含水率等进行反演计算,降低了反演结果的可靠性。
为解决上述连通性研究方法存在的问题,本文建立了一种多层油藏水驱开发井间连通性反演模型,该模型能够对水驱开发各种动态指标(如含水率、产油量和流压等)进行模拟计算,在此基础上结合优化算法进行动态拟合计算,可快速获取井间分层连通参数、实时反映井间注采关系和油水流动动态。
1 连通性模型的建立
借鉴Gherabati等提出的方法[17],对油藏注采系统进行简化表征,将油藏各层离散成一系列由井间传导率和连通体积等参数表征的井间连通单元(见图1)。其中,前者表示单位压差下的渗流速度,能够较好地反映井间的平均渗流能力和优势传导方向,后者表征了单元的物质基础,能够反映井间水驱控制范围和体积。可知井间连通单元传导率越小,控制体积越大,则在同等生产压差下,该单元无水生产时间越长,反之则见水突破较早。然后,以连通单元为模拟对象建立物质守恒方程,考虑定液或定压生产模式,进行压力求解,计算井间流量;最后,结合油水两相前缘推进理论进行饱和度追踪,计算井点处的分层生产动态指标。

图1 井间连通单元示意图
1.1压力及井间流量的计算
考虑连通单元内油水流入流出以及油、水、岩石压缩性,并忽略层间窜流、毛细管力作用,以第i口井为对象,其油藏条件下物质平衡方程为:

对(1)式整理可得:

对(2)式进行隐式差分可得:

根据渗流理论[18],传导率和连通体积随时间而改变,其可根据上一时刻压力或饱和度进行估算:
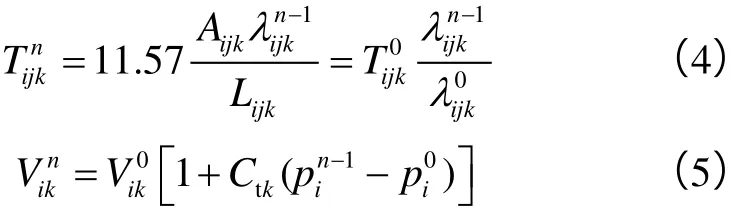

求解(3)式时,对于源汇项,存在定液和定压生产两种内边界条件,且实际模拟计算时会存在两者间相互转换,下面给出两种条件下的压力求解过程。
1.1.1定液生产求解
定液生产即qin为已知常数,(3)式经整理得:
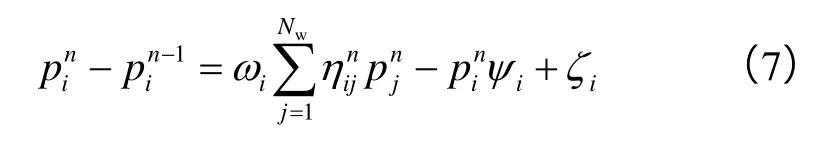
其中

n时刻与n-1时刻压力关系可表示为:

通过求解(8)式即可获得n时刻各单井泄油区的平均压力,进而可以得出各井间连通单元内流体流动方向及流量:

1.1.2定压生产求解
井底流压为已知常数,此时需要求得各井的生产(或注水)指数,其可通过各连通方向的生产指数迭加算得。以第i井为例,其和第j井在第k层上的连通单元所形成的泄油区如图2中灰色区域所示,由渗流理论[18],该连通方向的生产指数为:

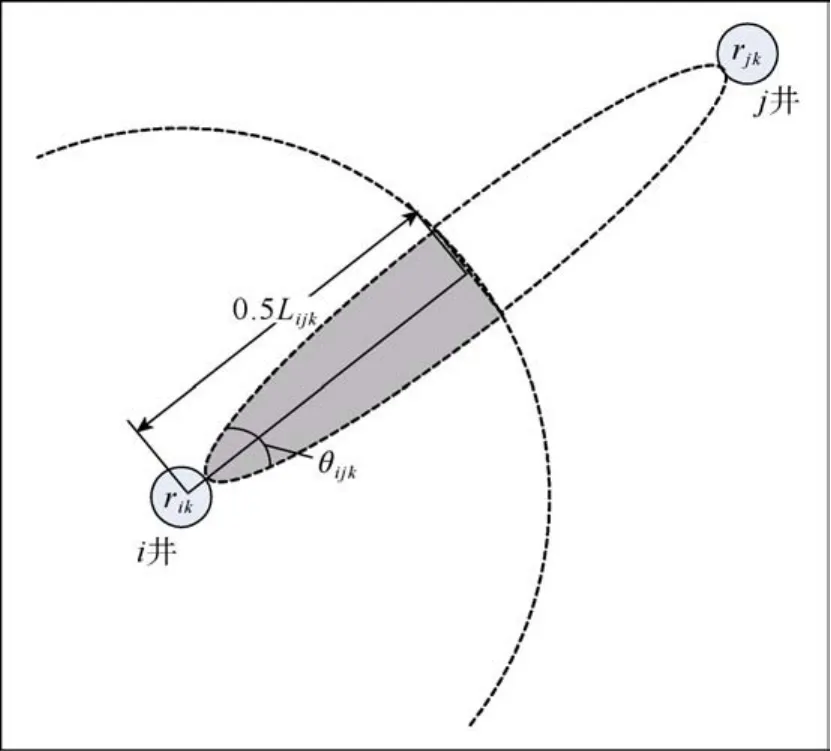
图2 单井泄油区示意图
此外,由于传导率和连通体积满足:
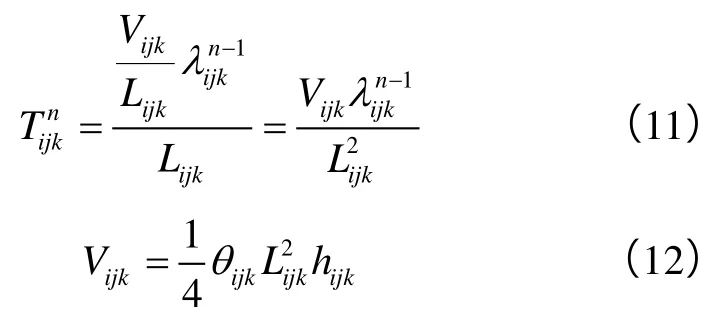
综合(10)式—(12)式可得:



将该式代入(3)式可得:

(16)式经化简得:

由(17)式可得,n时刻与n-1时刻压力关系为:
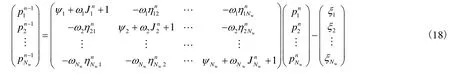
求解(18)式可得各时刻单井平均压力,并由(9)式计算连通单元的流量,同时由(15)式通过井底流压可反算单井日注采量。
实际计算中当采用定液生产模式、模型参数偏离正常范围较远时,由(15)式计算出的井底流压较小甚至出现负值,这明显不符合事实。对此,可对井底流压设置一个下限值(如大气压或泡点压力),当井底流压小于此值,说明此井难以满足定液生产,需转成定压生产模式,且井底流压取该下限值。
1.2含水饱和度追踪计算
本文模型将每个时间步内连通单元内部的流动近似看成稳定渗流,连通单元内油水流动主要沿着井间最大压降梯度方向,对连通单元内的饱和度计算可近似看成一维两相渗流问题。由贝克莱前缘推进理论[15]可知距离注入端任意位置处含水饱和度与累计流量间满足:
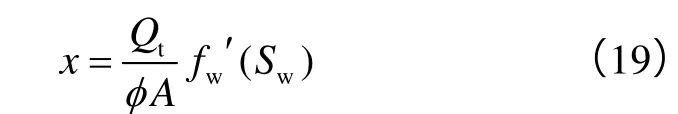
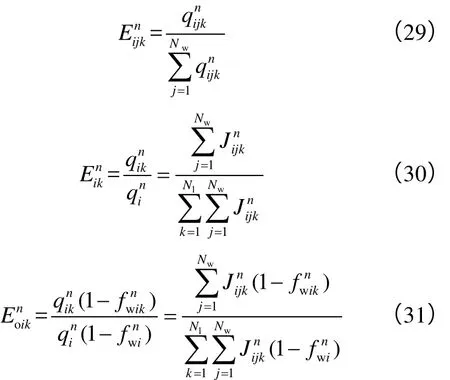
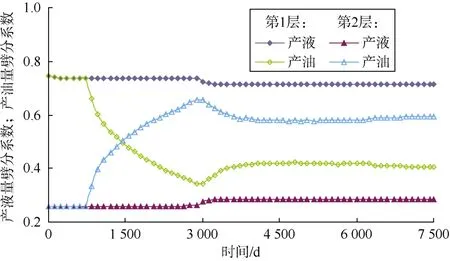
另取一点xu,其为x的上游点,满足xu 由上述两式可得, 定义Fv为从xu流入到x的无因次累计流量,即: 则由(21)式可得: (23)式说明:储集层中某位置的含水率导数是其上游值加上流入两者间控制单元的无因次累计流量的倒数。 由此可得,某井点的含水饱和度可由其所有上游井点的含水饱和度追踪求得,与下游井点无关。通过前述压力求解计算可以判断各口井的上游井点,考虑第k层、第i井和第j井之间的连通单元,若pjn>pin,即第j井为第i井上游井,应用(23)式可得: 当发生关停井或油井转注等措施调整时,油藏压力分布和流动方向将发生较大变化,上、下游节点会发生对换,此时,Fvijk应取为压力变化之后的无因次累计流量,重新计算后,为实现计算稳定性,根据一些学者研究[20],其值取计算值和上一时刻井点含水率导数值的最小值,即: 获得fw¢(Swijkn)后可反算出第i井在第k层来自于第j井方向的含水率fwijkn,依次计算出各个上游方向的含水率后,可得到第i井在k层的综合含水率: 获得分层含水率后,结合各层的日产液量就可计算整体含水率,各层日产液(注入)量可利用生产(注入)指数进行劈分算,得: 确定单井各层日产液和含水率后,其综合含水率为: 求得各井分层产液量及含水率、综合含水率后,就可以进一步计算其他单井和区块的分层、整体动态指标。本文模型还能实时计算注采井间流量分配系数、单井分层产液、产油、注水劈分系数等信息,实现了对油藏平面、纵向流动动态的刻画,这些都是矿场动态分析和剩余油评价的重要基础数据,也是油气田开发研究的难点问题[21-23]。这里的流量分配系数能够表征不同时刻注采井之间的连通性,与当前连通性模型中的连通性系数是定值相比,能更准确地反映工作制度及措施变化,便于分析油藏实际生产状况。这些动态指标计算表达式如下: 由以上模型建立过程可以看出,与当前连通性模型相比,本文模型较好地把握了水驱多层油藏油水渗流的本质特征,考虑因素更加全面、预测功能更加强大。相对于传统数值模拟方法,需要求解的压力方程维数较低,与井数相等,且饱和度追踪是以连通单元为对象、通过半解析方法求解,因此,整个过程运算量较小,计算快速、稳定,该模型可以近似看成是介于两种方法之间的中间模型。此外,油藏井网越完善,所建模型反映的油水动态与实际情况就越接近,因而,实际计算中对于注采井网不完善部分,可人为补充产量为0的虚拟井进行完善。 基于所建立的连通性模型进行水驱开发动态指标的计算,其结果取决于各井间连通单元的特征参数,实际应用中通过优化这些参数使模型计算动态与实际历史动态相吻合即可实现模型参数的反演求解,为此定义如下最小化问题: 满足: 优化上述问题的关键是获得目标函数的梯度,当连通单元较少时,可采用简单的有限差分近似梯度法计算[24];对于连通单元较多的大规模优化问题,采用随机扰动梯度法(SPSA)[25-27]计算,该方法与有限差分梯度法近似,通过对模型参数进行同步随机扰动计算获取近似梯度,所得近似梯度恒为上山方向,且期望值为真实梯度[25-26],其计算表达式如下: 在实际运用中,为了提高近似梯度与真实梯度的逼近程度,可以使用多次扰动梯度的平均值进行优化计算。获取梯度后,本文采用传统的投影梯度算法[27-28]对该约束优化问题进行迭代求解,该方法计算简单、且能保证每次迭代后的解都是可行解,其迭代公式为: 应用本文所建模型,笔者借助油藏数值模拟技术对三维油藏模型进行了分层井间连通性反演。所建油藏模型划分网格为21×21×2,X、Y和Z方向的网格尺寸分别为20 m、20 m和10 m。油藏模型两层的平面渗透率分布有明显的差异,第1层和第2层层内渗透率级差分别为165.0和171.6(见图3),初始油藏束缚水饱和度为0.2,油水黏度分别为20.0 mPa·s和1.0 mPa·s。油藏采用五点法井网,含5口注水井和4口生产井。采用成熟的Eclipse数值模拟软件对该油藏进行了生产动态模拟运算,模拟生产时间为7 500 d,W1、W2、W3、W4、W5井的注入量都为40 m3/d,保持不变;P1、P2、P3、P4井前3 000 d的采液量为50 m3/d,为体现工作制度等措施变化的影响,3 000 d后对P1 和P2井提液生产、P3和P4井降液生产,P1、P2、P3、P4井采液量分别为80、60、40、20 m3/d,油藏整体注采平衡,最终含水率达到81.0%。 图3 油藏渗透率分布 选取前6 000 d的单井产油速度和全区累产油等指标用于进行动态拟合优化,后1 500 d数据用来对反演后的模型预测效果进行检验。优化过程中采用SPSA方法估算梯度,其目标函数优化过程见图4,经过70步迭代优化以后,目标函数趋于收敛,整个优化过程耗时5 min左右。从图5所示生产动态拟合和预测结果可以看出,经过优化后本文模型取得了较好的动态拟合效果,模型预测值也能很好地匹配生产动态,验证了该模型具有较好的外推性,可以用于后期水驱开发动态预测。 图4 目标函数优化过程 最终反演所得的模型参数如图6所示,图中数据直观表征了各油层内井间的平均传导率和连通体积等参数大小,其中的红色连线表示优势传导方向;蓝色连线表示传导能力一般;灰色连线表示传导能力较差。可以看出,在第1层,由于注水井W1井附近区域物性较差,渗透率较小(见图3),反演所得W1井与周围井的井间传导率值也小,其与周围各井传导率平均值为0.026 m3/(d·MPa);相反,由于P4渗透率较大,与周围井的井间传导率较大,其与周围各井传导率平均值为0.108 m3/(d·MPa),尤其是其与注水井W5间的传导率最大,为0.160 m3/(d·MPa)。同理,第2层中W2井与周围井的井间传导率较小,P4井与周围井的传导率相对较大。反演结果与油藏实际地质特征相符合,验证了本文方法的可靠性。同时,本文方法所得的井间连通体积参数为评价井间水驱波及效率,以及后期调剖或调驱等方案实验区的优选和堵剂用量设计等提供了依据。 图5 模型动态拟合和预测结果 图6 各层井间连通单元参数反演结果(括号中第1个数值为传导率,单位为m3/(d·MPa),第2个数据为连通体积,单位为104m3;红色连线表示优势传导方向;蓝色连线表示传导能力一般;灰色连线表示传导能力较差) 此外,基于反演后的模型还能实时获取分层注采井间流量分配系数、油井产液产油劈分系数等。其中,注水井W5与周围油井间的注水劈分系数变化如图7所示。可以看出,W5井在第1层内注水主要流向油井P1,在第2层则主要流向油井P2,由于3 000 d后P1井提液、P4井降液生产,W5井与P1井分配系数在此之后增加,由最初的0.36增大到0.58,而其与P4井分配系数则由0.28下降到0.09,模型计算注水分配系数与实际注采变化特征相吻合,且避免了当前连通性模型难以考虑分配系数时变性的局限性。 图7 W5井与周围油井间的流量分配系数曲线 油井P1井产液、产油分层劈分系数曲线见图8。可以看出,其第1层产液劈分贡献最大,这与其在该层渗透率较高的物性特征相符,但由于其在该层受水井W5影响较大,W5井注入水向该井快速窜进,约720 d后注入水突破,造成其产油量不断下降,含水率不断上升,该层产油贡献逐渐降低,最终约为0.42,低于第2层产油贡献。 图8 P1井分层产液、产油劈分系数曲线 所建立的井间连通性反演模型以连通单元为模拟对象,将数值计算转化为一系列一维问题求解,可实现水驱开发动态指标的快速计算,突破了传统连通性模型只能预测产液动态的局限性,且模型反演参数具有明确的地质意义,能够分层表征井间地层参数和连通特性,可为识别优势传导方向、评价井间水驱波及体积以及后期调剖或调驱等措施方案设计等提供重要依据。 应用所提出的优化算法进行算例应用取得了较好的动态拟合效果,反演的连通模型参数与实际油藏地质特征相吻合;基于反演后的模型获取的分层井间流量分配系数、产液产油劈分系数等信息能够实时刻画油藏井间油水流动关系,相比目前连通性方法,能更全面地反映井间相互作用和实际生产措施变化。 本文模型对水驱开发生产动态具有较好的预测功能,因此,其可被进一步用于油藏开发注采参数优化控制等研究[27-28],且该模型的方法思路也可进一步拓展到聚合物驱、气驱等开发方式的油藏井间连通性分析及动态预测。 符号注释: A——渗流横截面积,m2;Aijk——k层第i井和第j井间的平均渗流截面积,m2;Cd——动态协方差阵;Ctk——油藏k层的综合压缩系数,实际动态指标向量;第i井和第j井间在第k层的流量分配系数、第i井第k层的日产液劈分系数和第i井第k层的日产油劈分系数;fw——含水率,f;fwi——第i口井的综合含水率,f;fwijk——第i井在第k层来自于第j井方向的含水率,f;fwik——第i口井第k层的综合含水率,f;Fv——无因次累计流量;Fvijk——从第j井流向第i井的无因次累计流量,其可由各时刻连通单元的瞬时流量qijkn累加求得;g——有限差分或随机扰动近似梯度;hijk——第i井和第j井在第k层的平均有效厚度,m;i,j——井序号;I——单位阵;Ji——第i井的生产指数,m3/(d·MPa);Jijk——第i井和第j井间连通方向的生产指数,m3/(d·MPa);k——层序号;Kijk——第i和j井在第k层的平均渗透率,10-3μm2;Kro,Krw——油、水的相对渗透率;Lijk——第i和j井在第k层的距离,m;m——由连通特征参数组成的向量;n——时间节点;Nw——注采井数;Nwu——第i井在第k层的上游井点数;Nl——油层数;O——待优化目标函数;pi,pj——第i和j井在泄油区内的平均压力,MPa;pwfi——第i井的井底流压,MPa;P——约束条件系数矩阵;qi——单井流速,注入为正、产出为负,m3/d;qik——第i井第k层的日产液(注入)量,m3/d;qijk——第i和j井间在第k层的流速,m3/d;Qt——累计注入量,m3;rik——第i井在第k层的井筒半径,m;sik——第i井在第k层的表皮因子;s(m)——连通模型预测的动态指标向量;Sw——位置x处的含水饱和度,f;Swik——第i井在第k层的含水饱和度,f;Swijk——第k层从第j井追踪到第i井处的含水饱和度,f;Swjk——第j井在第k层的含水饱和度,f;Swu——xu处的含水饱和度,f;t——生产时间,d;Tijk——第k层、第i井和第j井间的平均传导率,m3/(d·MPa);Ti1k——第k层、第i井和第1井间的平均传导率,m3/(d·MPa);Vik——第i井在第k层的泄油体积,m3;Vijk——第i井和第j井在第k层的连通体积,m3;Vi1k——第i井和第1井间的连通体积,m3;Vik——第i井在第k层的控制体积,m3;VR——油藏总孔隙体积,m3;x——渗流位置,m;ml——第l个迭代步的模型参数;g——迭代步长;Δt——时间步长,d;Dl——服从参数为±1的对称Bernoulli分布扰动向量;εl——扰动步长;θijk——连通单元近似扇形的弧度,rad;λijk——第k层、第i井和第j井间的流度,10-3μm2/(mPa·s);λik,λjk——第i井和第j井在第k层的流度,10-3μm2/(mPa·s);μok,μwk——第k层的油、水黏度,mPa·s;f——油藏孔隙度,f。 参考文献: [1] 康志宏, 陈琳, 鲁新便, 等. 塔河岩溶型碳酸盐岩缝洞系统流体动态连通性研究[J]. 地学前缘, 2012, 19(2): 110-120. KANG Zhihong, CHEN Lin, LU Xinbian, et al. Fluid dynamic connectivity of karst carbonate reservoir with fracture & cave system in Tahe oilfield[J]. Earth Science Frontiers, 2012, 19(2): 110-120. [2] 赵伦, 王进财, 陈礼, 等. 砂体叠置结构及构型特征对水驱规律的影响: 以哈萨克斯坦南图尔盖盆地Kumkol油田为例[J]. 石油勘探与开发, 2014, 41(1): 86-94. ZHAO Lun, WANG Jincai, CHEN Li, et al. Influences of sandstonesuperimposed structure and architecture on waterflooding mechanisms: A case study of Kumkol Oilfield in the South Turgay Basin, Kazakhstan[J]. Petroleum Exploration and Development, 2014, 41(1): 86-94. [3] 封从军, 鲍志东, 杨玲, 等. 三角洲前缘水下分流河道储集层构型及剩余油分布[J]. 石油勘探与开发, 2014, 41(3): 323-329. FENG Congjun, BAO Zhidong, YANG Ling, et al. Reservoir architecture and remaining oil distribution of deltaic front underwater distributary channel[J]. Petroleum Exploration and Development, 2014, 41(3): 323-329. [4] 杜鹃, 杨树敏. 井间微地震检测技术现场应用效果分析[J]. 大庆石油地质与开发[J]. 2007, 26(4): 120-122. DU Juan, YANG Shumin. Analysis to the field application effect of inner well microseismic monitoring technique[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 26(4): 120-122. [5] 易斌, 崔文彬, 鲁新便, 等. 塔河油田碳酸盐岩缝洞型储集体动态连通性分析[J]. 新疆石油地质, 2011, 32(5): 469-472. YI Bin, CUI Wenbin, LU Xinbian, et al. Analysis of dynamic connectivity on carbonate reservoir with fracture and cave in Tahe field, Tarim basin[J] Xinjiang Petroleum Geology, 2011, 32(5): 469-472. [6] HEFFER K J, FOX R J, MCGILL C A, et al. Novel techniques show links between reservoir flow directionality, earth stress, fault structure and geomechanical changes in mature waterfloods[R]. SPE 30711, 1995. [7] ALBERTONI A, LAKE L W. Inferring interwell connectivity only from well-rate Fluctuations in water floods[R]. SPE 83381, 2003. [8] YOUSEF A A, GENTIL P, JENSEN J L, et al. A capacitance model to infer interwell connectivity from production and injection rate fluctuations[R]. SPE 95322, 2005. [9] YOUSEF A A, JENSEN J L, LAKE L W. Integrated interpretation of interwell connectivity using injection and production fluctuations[J]. Mathematical Geosciences, 2009: 81-102. [10] WEBER D, EDGAR T F, LAKE L W, et al. Improvements in capacitance-resistive modeling and optimization of large scale reservoirs[R]. SPE 121299, 2009. [11] SAYARPOUR M, KABIR, C S, LAKE L W. Field applications of capacitance-resistance models in waterfloods[R]. SPE 114983, 2009. [12] NGUYEN A P, KIM J S, LAKE L W, et al. Integrated capacitance resistive model for reservoir characterization in primary and secondary recovery[R]. SPE 147344, 2011. [13] SALAZAR M, GONZALEZ H, MATRINGE S, et al. Combining decline-curve analysis and capacitance-resistance models to understand and predict the behavior of a mature naturally fractured carbonate reservoir under gas injection[R]. SPE 153252, 2012. [14] CAO F, LUO H S, LAKE L W. Development of a fully coupled two-phase flow based capacitance resistance model(CRM)[R]. SPE 169485, 2014. [15] MORENO G A, LAKE L W. On the uncertainty of interwell connectivity estimations from the capacitance-resistance model[J]. Petroleum Science, 2014, 11(2): 265-271. [16] 赵辉, 李阳, 高达, 等. 基于系统分析方法的油藏井间动态连通性研究[J]. 石油学报, 2010, 31(4): 633-636. ZHAO Hui, LI Yang, GAO Da, et al. Research on reservoir interwell dynamic connectivity using systematic analysis method[J]. Acta Petrolei Sinica, 2010, 31(4): 633-636. [17] GHERABATI S A, HUGHES R G, ZHANG H, et al. A large scale network model to obtain interwell formation characteristics[R]. SPE 153386, 2012. [18] 张建国, 杜殿发, 侯建, 等. 油气层渗流力学[M]. 东营: 中国石油大学出版社, 2009. ZHANG Jiangguo, DU Dianfa, HOU Jian, et al. Oil and gas seepage mechanics[M]. Dongying: China University of Petroleum Press, 2009. [19] 李淑霞, 谷建伟. 油藏数值模拟基础[M]. 东营: 中国石油大学出版社, 2009. LI Shuxia, GU Jianwei. The basis for reservoir numerical simulation[M]. Dongying: China University of Petroleum Press, 2009. [20] 宋考平, 吴玉树, 计秉玉. 水驱油藏剩余油饱和度分布预测的φ函数法[J]. 石油学报, 2006, 27(3): 91-95. SONG Kaopin, WU Yushu, JI Bingyu. A φ-function method for estimating distribution of residual oil saturation in water drive reservoir[J]. Acta Petrolei Sinica, 2006, 27(3): 91-95. [21] 李成勇, 柳金城, 李晓茹, 等. 多层合采油藏油水井产量劈分原理及应用[J]. 大庆石油地质与开发, 2010, 29(1): 55-59. LI Chengyong, LIU Jincheng, LI Xiaoru, et al. Principles and application of production allocation for oil and water wells in multilayer commingled development oil reservoir[J]. Petroleum Geology & Oilfield Development in Daqing, 2010, 29(1): 55-59. [22] 李凤琴, 刘丽琼, 丁全胜, 等. 分层累计吸水量劈分方法研究[J].河南石油, 2005, 19(5): 28-29. LI Fengqin, LIU Liqiong, DING Quansheng, et al. A study on calculation of accumulative water-intake rate of separate layer[J]. Henan Petroleum, 2005, 19(5): 28-29. [23] 曹光胜. 厚层块状稠油油藏产量劈分方法研究[J]. 特种油气藏, 2006, 13(1): 58-60. CAO Guangsheng. Study on production split in thick massive heavy oil reservoir[J]. Special Oil & Gas Reservoirs, 2006, 13(1): 58-60. [24] WANG C H, LI G M, REYNOLDS A C. Production optimization in closed-loop reservoir management[R]. SPE 109805, 2007. [25] SPALL J C. Adaptive stochastic approximation by the simultaneous perturbation method[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1839-1853. [26] ZHAO Hui, LI Yang, YAO Jun, et al. Theoretical research on reservoir closed-loop production management[J]. Science China: Technological Sciences, 2011, 54(10): 2815-2824. [27] 赵辉, 李阳, 康志江. 油藏开发生产鲁棒优化方法[J]. 石油学报, 2013, 34(5): 947-953. ZHAO Hui, LI Yang, KANG Zhijiang. Robust optimization in oil reservoir production[J]. Acta Petrolei Sinica, 2013, 34(5): 947-953. [28] ZHAO H, CHEN C H, DO S, et al. Maximization of a dynamic quadratic interpolation model for the production optimization[J]. SPE Journal, 2013, 18(6): 1012-1025. (编辑张敏) An interwell connectivity inversion model for waterflooded multilayer reservoirs ZHAO Hui1, KANG Zhijiang2, SUN Haitao1, ZHANG Xiansong3, LI Ying1 Abstract:In view of the limitations that the current connectivity model can only forecast the fluid production dynamic change, can’t calculate the dynamics of oil and water phases, and can’t analyze the connectivity between wells layer by layer, this study establishes a new interwell connectivity model for multilayer reservoirs which can simulate dynamics of oil and water between wells. The model hierarchically separates the reservoir system into a series of interwell connecting units characterized by parameters such as conductivity and control volume, and by using the material balance equation, the pressure and interwell flow at constant liquid production and constant pressure is calculated with the connecting unit as simulation object, which are combined with the frontal advance theory to establish interwell saturation tracking calculation method, and finally water production dynamics of every layer at well points can be worked out. On this basis, using simultaneous perturbation stochastic approximation method and gradient projection method, a model parameter inversion method is set up by dynamic fitting. The application cases show that the model has good dynamic fitting and prediction effect, inversed model parameters and the actual geological parameters coincide with well, verifing the validity of the method. Compared with the current connectivity method, it can obtain the real-time model of hierarchical interwell flow rate distribution coefficient, liquid production of single well and oil split coefficient and other information, and reflect the reservoir horizontal and vertical oil-water flow relation more accurately, providing guidance for production measure adjustment in oilfield. Key words:multilayer reservoir; interwell conectivity; inversion model; interwell connecting unit; interwell flow rate distribution coefficient; oil split coefficient 基金项目:国家科技重大专项(2011ZX05014);国家自然科学基金资助项目(51344003) 中图分类号:TE319 文献标识码:A 文章编号:1000-0747(2016)01-0099-08 DOI:10.11698/PED.2016.01.12 第一作者简介:赵辉(1984-),男,山东乐陵人,博士,长江大学石油工程学院副教授,主要从事油气田开发、油藏工程及优化控制工程方面的研究。地址:湖北省武汉市蔡甸区大学路一号,长江大学石油工程学院,邮政编码:430100。E-mail: zhaohui-712@163.com 收稿日期:2015-01-29修回日期:2015-12-08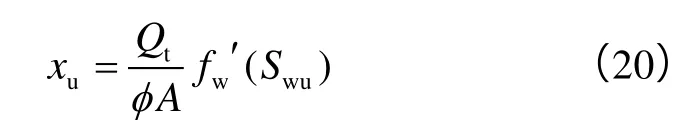

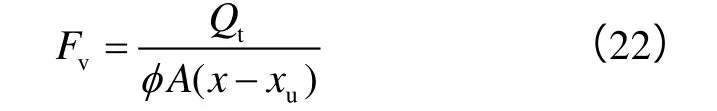
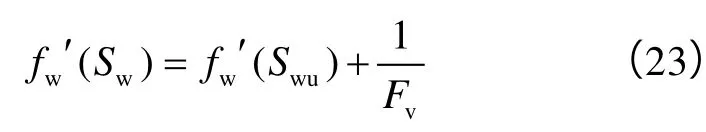

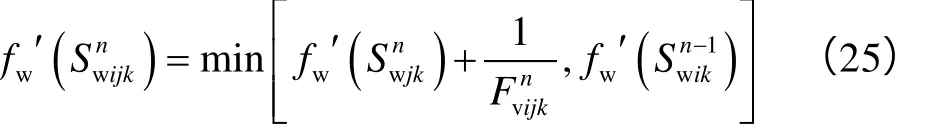

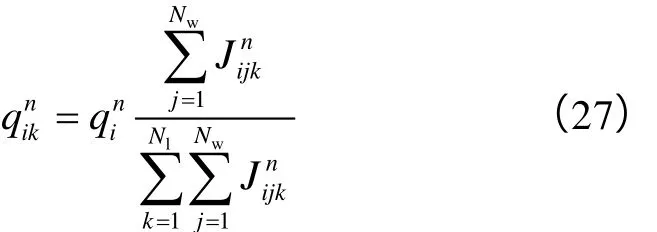

2 模型参数反演方法


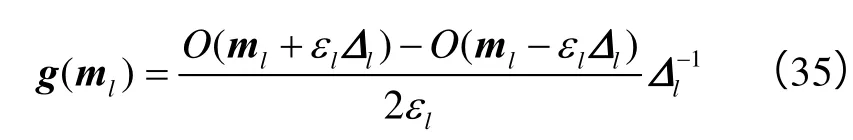

3 计算实例





4 结论
(1. College of Petroleum Engineering, Yangtze University, Jingzhou 434023, China; 2. Sinopec Exploration & Production Research Institute, Beijing 100728, China; 3. State Key Laboratory of Offshore Oil Exploitation, Beijing 100727, China)
