基于实验设计的行人保护小腿优化

胡远志，雷　雨，刘　西，周　林，刘宗成，朱红霞

(1.重庆理工大学 车辆工程学院 汽车零部件先进制造技术教育部重点实验室，重庆　400054;2.东风小康汽车有限公司，重庆　400033)



基于实验设计的行人保护小腿优化

胡远志1，雷雨1，刘西1，周林2，刘宗成2，朱红霞2

(1.重庆理工大学 车辆工程学院 汽车零部件先进制造技术教育部重点实验室，重庆400054;2.东风小康汽车有限公司，重庆400033)

摘要：按照我国行人保护法规建立了某车型行人保护小腿碰撞有限元模型，提出了增加吸能盒和副保险杠的结构优化措施。通过对吸能盒厚度、屈服强度和与保险杠蒙皮的距离进行全因子实验设计，初步找到了优化的方案。在此基础上构造2阶响应面模型，采用序列二次规划方法快速地找到了最优的结构优化组合。仿真对比结果表明：相比初始模型和初步优化组合，采用这种方法得出的最优解效果更好。

关键词：行人小腿；吸能盒；全因子实验；序列二次规划

汽车行人事故中行人腿部是最容易受到伤害的部位之一。2009年10月发布的推荐性国家标准GB/T34550—2009《汽车对行人的碰撞保护》规定，在行人腿部碰撞测试中评价行人小腿伤害程度时主要使用3个指标：胫骨加速度、膝部弯曲角度和膝部剪切位移。针对如何减小行人小腿伤害的3个指标，国内外专家做了大量研究[1-7]，主要采用合理设计、布置和优化保险杠前部与小腿碰撞相关的零部件的方法。

本文针对某车型进行行人保护小腿碰撞仿真分析，提出了一种优化方法，即在原状态的基础上增加副保险杠和吸能盒，然后以吸能盒厚度、屈服强度以及吸能盒与保险杠蒙皮的距离为设计变量，以腿部伤害的3个评价指标最小化为目标进行全因子实验，并构造响应面模型，最后通过序列二次规划法优化得到最优的组合，并对其进行验证。

1行人保护小腿建模与仿真

对本次仿真所使用的模型进行了正面碰撞对标分析，部分对标分析曲线如图1、2所示，可见模型具有较强的可信度。汽车上与行人保护小腿有关的部分主要是在碰撞过程中会与小腿接触的部分，包括保险杠、翼子板、大灯、冷凝器、进气格栅和防撞横梁等部件。对目标车型进行处理，保留上述主要部件，只截取车身前面部分，这样有助于节省计算时间。将车辆底部和后面截断处的6个自由度全部约束。

按照法规要求，小腿冲击器以40 km/h的速度撞击车辆保险杠区域，并以法规规定的3个评价指标对小腿伤害进行评价。仿真模型及仿真碰撞结果如图3～6所示。

图1　刚性墙力对标曲线

图2　右后部地板对标曲线

图3　小腿碰撞有限元模型

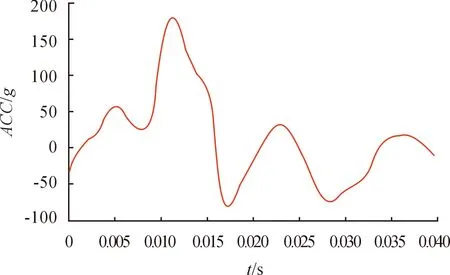
图4　胫骨加速度曲线

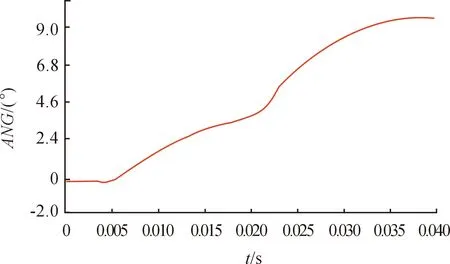
图5　膝部弯曲角度曲线

图6　膝部剪切位移曲线

由图4～6可以看出：小腿弯曲角度(ANG)最大为9.67°，剪切位移(DISP)最大为1.569 mm，符合法规要求，但是加速度(ACC)最大值为180.650g，超过法规规定值(170g)，最大的峰值出现在0.012 s小腿撞击防撞横梁时，而加速度曲线在0.005 s小腿冲击器碰撞保险杠蒙皮时出现小的峰值。因此，为满足法规的要求，需要对车辆前端进行适当的结构优化。

2前端结构优化和全因子实验模型分析

为了减小加速度，需要在保险杠蒙皮后、保险杠横梁前增加1个吸能盒，吸收碰撞能量，防止小腿直接撞上防撞横梁。为了减小弯曲角度，在下端采用副保险杠结构。副保险杠固定在冷凝器下部横梁上，在水平方向尽可能靠近保险杠蒙皮，在Z方向尽可能布置在小腿胫骨质心以下，如图7所示。

图7　吸能盒及副保险杠

采用上述结构能很好地吸收碰撞能量。但是在实际工程中，工程师需要精确确定吸能盒的厚度和屈服强度以指导工程设计[8]。吸能盒的厚度和屈服强度的不同组合以及吸能盒与保险杠蒙皮的距离在一定程度上影响吸能的效果。

为了得到设计参数的最优组合，采用实验设计方法，在参数允许范围内构造1个3因素3水平的全因子实验，响应参数即为小腿的3个评价指标。如表1所示，设计水平的中间一组为初始变量。全因子实验的仿真结果如表2所示。

表1　实验设计参数

表2　全因子实验结果

续表

实验编号THIC/mmSIGY/MPaDIST/mmACC/gANG/(°)DISP/mm100.61725133.5224.651.203110.617213155.4294.531.273120.617221161.6484.331.485130.62025141.2644.721.185140.620213162.9794.611.234150.620221169.1564.421.470160.62325150.6194.791.165170.623213172.1464.681.126180.623221178.2114.411.466190.81725194.2814.781.070200.817213212.8254.441.079210.817221212.0254.241.564220.82025205.7154.741.046230.820213222.6984.461.056240.820221220.7974.311.593250.82325217.9584.711.067260.823213233.0654.451.107270.823221212.3034.281.596

由全因子实验结果可知：在27组实验中，变量水平的改变对加速度的影响最大，对弯曲角度和剪切位移的影响很小；如果忽略对后两项的影响，可以得出第10组的效果最好，3个指标都满足法规的要求。

同时对3个因素进行主效应[9]分析，结果如图8～10所示。由图8～10可见：对加速度而言，3个因素对其影响的趋势是相同的，但是厚度对加速度的影响最大；对弯曲角度来说，前两个因素对其影响的趋势是相同的，距离对其影响相反，并且距离对弯曲角度的影响相比前两者大；前两个因素对剪切位移的影响趋势也是相同的，同样，距离对剪切位移的影响是3个因素中最大的。

图8　对加速度的主效应分析

图9　对弯曲角的主效应分析

图10　对剪切位移的主效应分析

3吸能盒优化分析

在上述全因子实验的基础上利用响应面法构造2阶响应面模型[10]。响应面法是数理统计的一种方法，利用此方法可以构建一个近似模型，通过近似模型代替仿真模型进行优化求解以节省计算时间，快速地找到模型的最优解。响应法是目前研究最深入、应用最广泛的一种方法。通常2阶响应面表达式如下：

(1)

其中：a0为多项式响应面模型表达式的常数项；ai为第i个变量的待定系数；xi为第i个设计变量。

通过以上27个样本点建立的3个多项式响应面模型表达式如下：

ACC= 222.555 20-637.261 93 x1+

0.160 439 2 x2+6.619 890 3 x3+

(2)

ANG=2.785 187 8+5.623 715 3 x1+

0.012 077 8 x2-0.187 927 1 x3-

(3)

DISP=0.183 363 9-4.139 866 9 x1-

0.002 036 3 x2-0.064 896 x3+

(4)

为了判定响应面模型精度是否可靠，可以对其决定系数R2进行考察[11]。R2由式(5)决定

(5)

表3　多项式响应面的决定系数

由表3可知：所有决定系数均在0.9以上，精度较高，响应面模型可信。

在响应面模型的基础上对小腿伤害的3个指标进行优化。如果对3个指标同时进行优化，此即为一个多目标优化的问题。因为在之前的模型中，设计因素对弯曲角度和剪切位移影响不是很明显，故在此采用对3个指标依次优化的方法。优化方法采用序列二次规划方法(SQP)。SQP是传统全局优化方法中使用比较广泛的一种方法。

在第一次优化时，使DISP最小，ACC≤150g，ANG≤5°，即：

目标函数：MinimizeDISP

约束条件：ACC≤150

ANG≤5

设计变量：0.4≤THIC≤0.8

173≤SIGY≤233

5≤DIST≤21

第1次优化结果如表4所示，因素的取值和响应的结果从表4中可以得到。

表4　第1次优化结果

在第1次优化的基础上进行第2次优化，使ANG最小，DISP的取值在最优解的基础上扩大20%。如果扩大后的值大于全因子实验中的最大值，即以最大值为上限，ACC不变，即：

目标函数：MinimizeANG

约束条件：ACC≤150

DISP≤1.154×1.2=1.385

设计变量：0.4≤THIC≤0.8

173≤SIGY≤233

5≤DIST≤21

第2次优化的结果如表5所示。

表5　第2次优化结果

按照同样的方法进行第3次优化。

目标函数：MinimizeACC

约束条件：DISP≤1.385

ANG≤4.98

设计变量：0.4≤THIC≤0.8

173≤SIGY≤233

5≤DIST≤21

第3次优化的结果(表6)即为最终的优化结果。因为弯曲角度和剪切位移对因素变化的影响很小，故在优化过程中主要目标是优化加速度。在此优化结果中，加速度的值相比全因子实验中的最小值更小。

表6　第3次优化结果

得出最优的吸能盒设计参数之后，将其代入有限元模型中进行验证，同时进行初始模型、SQP优化模型和仿真优化模型对比，结果如表7所示。仿真优化模型和初始模型的腿部伤害指标曲线对比如图11～13所示，图中将法规规定值也标示出来。

表7　初始模型、SQP模型及仿真优化模型对比

由图11～13可以看出：优化模型在与保险杠蒙皮接触时产生一个较小的加速度，由于吸能盒与保险杠蒙皮间距较近，吸能盒很快开始吸能，故第1个加速度峰值比初始模型大，通过吸能作用，使小腿撞击到防撞横梁上的加速度变小；副保险杠减弱了小腿向保险杠底部的运动的趋势，给小腿一个反作用力，使小腿的弯曲角度增加到一定时停止。

图11　仿真模型优化前后加速度曲线

图12　仿真模型优化前后弯曲角度曲线

图13　仿真模型优化前后剪切位移曲线

4结束语

本文通过对某车型进行行人保护小腿的仿真分析，以吸能盒厚度、屈服强度和与保险杠蒙皮距离为设计变量进行全因子实验，得出了初步的优化组合。在此基础上，进一步利用响应面法构造2阶响应面模型，通过近似模型代替仿真模型，采用序列二次规划方法以节省计算时间，快速地找到了模型的最优解。通过对最优的结构优化组合进行仿真对比发现：相比初始模型和初步优化组合，用这种方法得出的最优解效果更好。因此，以全因子实验为基础进行序列二次规划优化，能快速地找到结构设计中的最优参数组合，可以解决工程上结构设计中的问题，对参数选择有指导作用。

该方法也存在一定的局限性，比如前期全因子实验设计仿真时间相对较长，序列二次规划方法的应用需要一定理论基础。为此，为方便工程师对该方法的应用，后续研究可以考虑开发相应的软件来提高使用的普及性和效率。

参考文献：

[1]张涛，喻赛，王玉超，等.针对行人小腿保护的SUV前保结构设计与优化[J].汽车工程学报，2013，3(2)：139-144.

[2]曾必强，胡远志，谢书港，等.保险杠与车身连接方式对行人保护的影响[J].汽车工程，2011，33(7)：594-597.

[3]沈玉婷，朱大勇.基于行人腿部伤害指标的保险杠参数分析[J].汽车技术，2007(10)：32-35.

[4]陈金华，黄向东，田晟.泡沫应变率对行人小腿碰撞性能的研究[J].汽车技术，2011(12)：32-36.

[5]DANIEL DE M B,ANDERSONS F.Design Style Influence on Pedestrian Leg Impacts[J].SAE Technical Paper,2009，36：67.

[6]BHAGAT M,CHALIPAT S.Influence of vehicle front end design on pedestrian lower leg performance for SUV class vehicle[J].SAE Technical Paper,2011(1)：84.

[7]胡远志，方锐，谢书港，等.行人保护冲击器有限元模型开发[J].汽车技术，2010(12):6-9.

[8]都雪静，韦丽苹，吸能盒盒体内部结构的改进[J]．重庆理工大学学报(自然科学)， 2015(12):7-12.

[9]洪清泉，赵康，张攀，等.OptiStruct & HyperStudy理论基础与工程应用[M].北京：机械工业出版社,2013.

[10]顾纪超.基于混合元模型的新型全局最优化方法及其在汽车设计中的应用[D].长沙：湖南大学，2011.

[11]赵敏，钟志华，周俊，等.回归分析方法在汽车侧碰安全性设计中的应用[J].汽车工程，2013，35(8)：706-710.

(责任编辑刘舸)

Optimization of Leg Pedestrian Protection Based on Design of Experiments

HU Yuan-zhi1, LEI Yu1, LIU Xi1, ZHOU Lin2, LIU Zong-cheng2, ZHU Hong-xia2

(1.School of Automotive Engineering, Key Laboratory of Advanced Manufacturing Technology for Automobile Parts, Ministry of Education, Chongqing University of Technology, Chongqing 400054, China;2.Dongfeng Sokon (DFSK) Motor Co., Ltd., Chongqing 400033, China)

Abstract:According to pedestrian protection regulations of our country, a model of leg pedestrian protection for a certain vehicle was established, and the structure optimization measures of adding energy absorbing box and additional bumper were provided. Based on the thickness, the yield strength and their distance to the bumper skin of the absorbing box, the full factorial design of experiments were performed to find the initial optimized scheme. Based on this, the second order response surface model was structured and sequential quadratic programming method was employed to quickly find the structure optimization. Finally, simulation found that the structure optimization obtained by this method shows better results, compared to the initial model and initial optimization combination.

Key words:pedestrian legform；energy absorber；full factorial design experiment; sequential quadratic programming

收稿日期：2015-10-27

基金项目：国家自然科学基金资助项目(51405050)；2015年重庆市重点产业共性关键技术创新专项资助项目(cstc2015zdcy-ztzx60010)；2015重庆市基础与前沿研究计划资助项目 (cstc2015jcyjA00048)；2015年重庆市高等教育教学改革研究资助项目(152032)；2013年重庆市科技人才培养计划资助项目(cstc2013kjrc-qnrc60002)；2012年汽车零部件先进制造技术教育部重点实验室开放课题资助项目(2012KLMT08)

作者简介：胡远志(1977—)， 男， 博士， 教授， 主要从事汽车主被动安全、CAE技术和耐久可靠性技术研究；通讯作者 刘西(1977—)，女，博士，副教授， 主要从事汽车主被动安全、人机工程研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.001

中图分类号：U462.2+2

文献标识码：A

文章编号：1674-8425(2016)05-0001-07

引用格式：胡远志，雷雨，刘西，等.基于实验设计的行人保护小腿优化[J].重庆理工大学学报(自然科学)，2016(5):1-7.

Citation format：HU Yuan-zhi, LEI Yu, LIU Xi,et al.Optimization of Leg Pedestrian Protection Based on Design of Experiments [J].Journal of Chongqing University of Technology(Natural Science)，2016(5):1-7.