基于EGARCH-GPD模型的沪深300指数的VaR度量

魏正元，李　娟，罗云峰

(重庆理工大学 数学与统计学院，重庆　400054)



基于EGARCH-GPD模型的沪深300指数的VaR度量

魏正元，李娟，罗云峰

(重庆理工大学 数学与统计学院，重庆400054)

摘要：结合经典的EGARCH模型和基于广义Pareto分布的极值理论，建立了一种新的EGARCH-GPD模型，并研究了新模型的动态VaR估计问题。沪深300指数VaR估计的返回测试结果表明：该EGARCH-GPD模型比传统的基于正态分布的EGARCH模型能更好地刻画金融数据分布的“厚尾”特征和波动率的时变性，在一定程度上提高了VaR估计的预测精度。

关键词：EGARCH模型；广义Pareto分布；POT；VaR；Kupiec失败率检验

近年来，随着信息技术的不断发展，经济和金融全球化的步伐不断加快，金融市场的波动性日趋激烈，对国家、企业的影响也越来越大，因此金融风险管理已经为越来越多的公司、部门、机构所重视，金融风险管理技术也成为当前研究的热点和难点。金融风险度量方法经过半个多世纪的发展已经取得了相当大的进步，尤其是随着复杂数学方法的成功运用，国内外学者提出了许多度量风险的方法，其中以VaR(value at risk)的使用最为广泛，其在现代金融风险管理中具有核心的地位。市场风险的VaR度量是指一个投资组合在某一给定的时间段内，以某个给定的概率α得到的所能承受的最大损失。换句话说，如果已知某一特定时间段内精确的 VaR，那么在这一时间段内发生比VaR更大的损失的概率就可以控制在α内。从统计学角度解释，VaR即是一随机变量的上侧α分位数。

如何估计收益率序列的波动率是VaR估计的核心问题之一。目前，在金融计量中，收益率序列波动率的估计绝大部分基于以Bollerslev为代表的学者们提出的一系列GARCH族模型[1]，其基本思想是金融时间序列在大的波动后紧接着是更大的波动，其波动性随时间的变化而变化[2]。Nelson[3]提出的EGARCH模型更体现了正和负的收益率的非对称效应，在一定程度上更准确地描述和预测了金融资产收益的波动性。

GARCH族模型中所采用的信息分布多为参数分布，例如正态分布、学生t分布、广义误差分布等。分布假设的合理性将直接影响VaR估计的准确性[4]。近年来发展起来的极值理论预先对数据不做分布假定，直接对尾部进行建模，而VaR关注的也是资产损益的尾部特征，这在一定程度上增加了VaR预测的精度[5]。Danielsson[6]用极值理论对VaR进行计算，将其与基于经验分布函数计算的VaR值进行对比，证明极值理论能有效提高VaR预测精度。Reiss[7]对极值理论在金融风险中的应用进行了具体的分析和论证。赵树然、任培民[8]在极值理论的基础上对参数进行了点估计，给出了 VaR 和CVaR的估计值，通过返回测试，证明了极值理论可以比较精确地度量VaR。在2012年的国际会议和金融工程中，WANG[9]进一步给出了基于极值理论的风险值估计的新方法。然而，极值理论的统计推断大都要求样本是独立同分布的，而在实际研究中，样本数据很难满足这一要求[10]。MCNILE和FREY[11]在具体的研究中发现，金融数据的标准化残差序列能有效满足独立、同分布的条件。

为对风险进行更加准确的度量，本文主要通过标准化残差序列，将经典EGARCH模型和基于GPD的极值理论结合起来，建立动态VaR估计模型。

1极值理论

本文采用的极值理论为基于广义Pareto分布的POT方法。该方法着重讨论对某个阈值的超出量。

定理1对于一个递增的阈值u，随机变量X1,X2,…,Xn的超越量分布函数Fu可由GPD近似：

上式中的Gξ,σ即为如下的广义Pareto分布(GPD):

(1)

其中σ>0，且当ξ≥0时，y≥0; 当 ξ<0 时，0≤y≤σ/ξ。这里 ξ 和 σ 分别是GPD的形状参数和尺度参数。

对GPD的参数进行估计后，给定上尾概率p，VaR可以由式(2)估计[12]。

(2)

其中:N为样本容量，即观测的总次数；Nu为超越阈值 u的次数。

2EGARCH-GPD模型

为了在模型中刻画正和负的资产收益率序列{rt,t=1,2,…}所引起的非对称效应，也即所谓的“杠杆效应”，1991年Nelson 在GARCH模型的基础上考虑加权的扰动，提出了如下的EGARCH 模型：

(3)

(4)

在EGARCH模型中，{εt}的分布无论是正态分布、学生t分布还是误差分布，均存在分布假设所带来的模型误差，当假设与实际偏差较大时，会直接影响到VaR估计的准确性。考虑到VaR的估计只涉及分布的尾部行为，而极值理论又可以在非参数的情况下对分布的尾部近似描述，因此本文在EGARCH模型的框架下，引入极值理论来描述{εt}分布的尾部行为，并借助GPD的VaR计算方法和EGARCH模型，实现基于EGARCH-GPD模型的VaR度量。

综上，基于EGARCH-GPD模型的VaR度量的具体操作流程为：

1) 对收益率序列建立EGARCH模型，借助正态分布或标准化学生t分布的新息过程εt，并利用极大似然法对参数μ, ω, αi, βj进行估计。

2) 将参数的估计值代入式(4)，通过迭代的方法求出σt，再由

得到εt的近似估计序列，称其为修正的残差序列。

5) 根据VaR的正齐次性和平移不变性[13]，得到EGARCH-GPD模型的VaR估计量，即

3实证分析

3.1数据与样本说明

本文采集的数据是沪深300指数2000-01-07—2015-04-03的日对数收益率，共计3 207个样本见图1。数据来源为锐思数据库www.resset.cn。

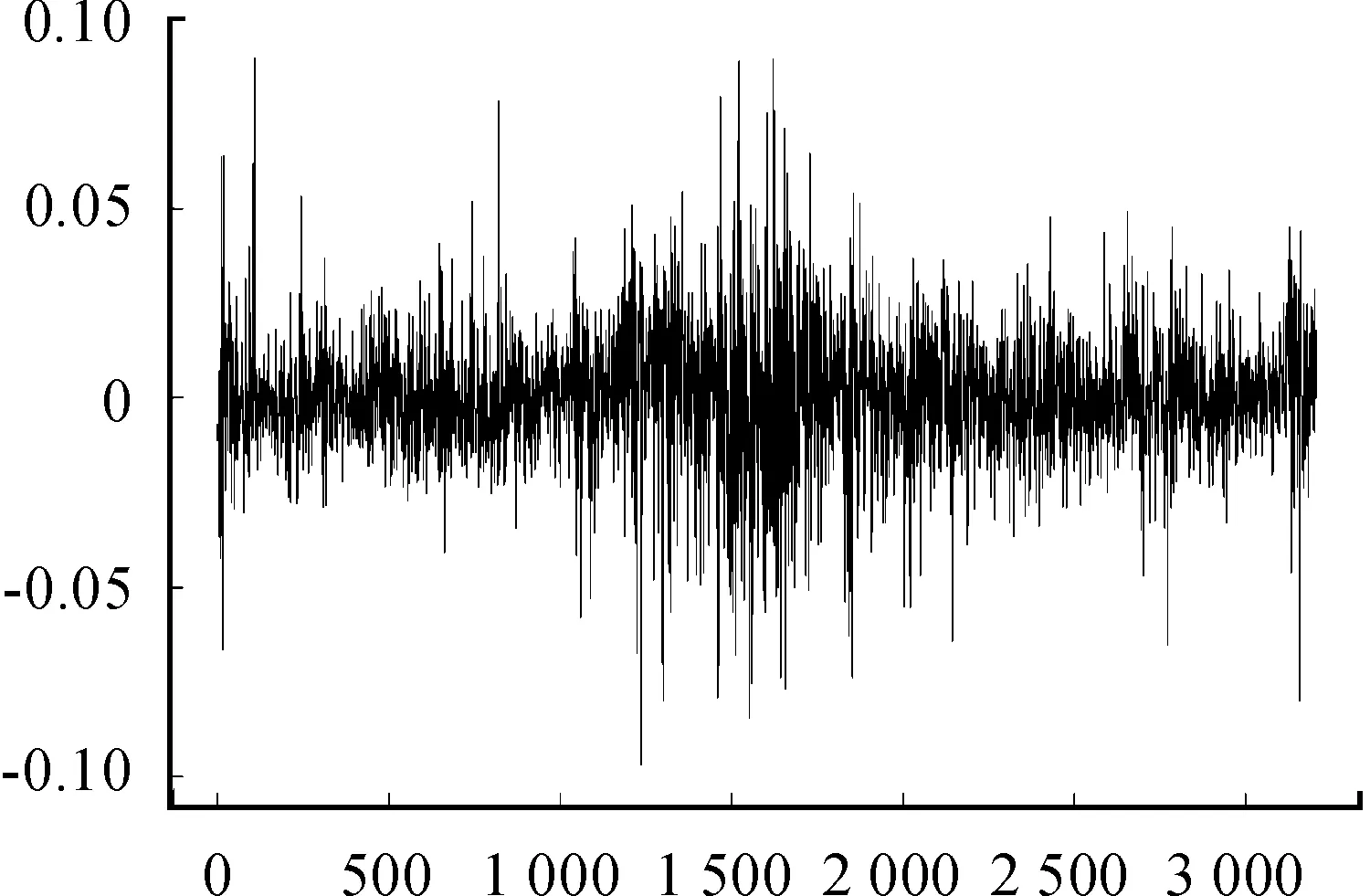
图1　沪深300指数从2000-01-07—2015-04-03的日对数收益率

表1列出了沪深300指数日对数收益率的基本统计量，峰度6.460 549>3，且其JB检验统计量的p值非常小，拒绝了正态性的原假设。

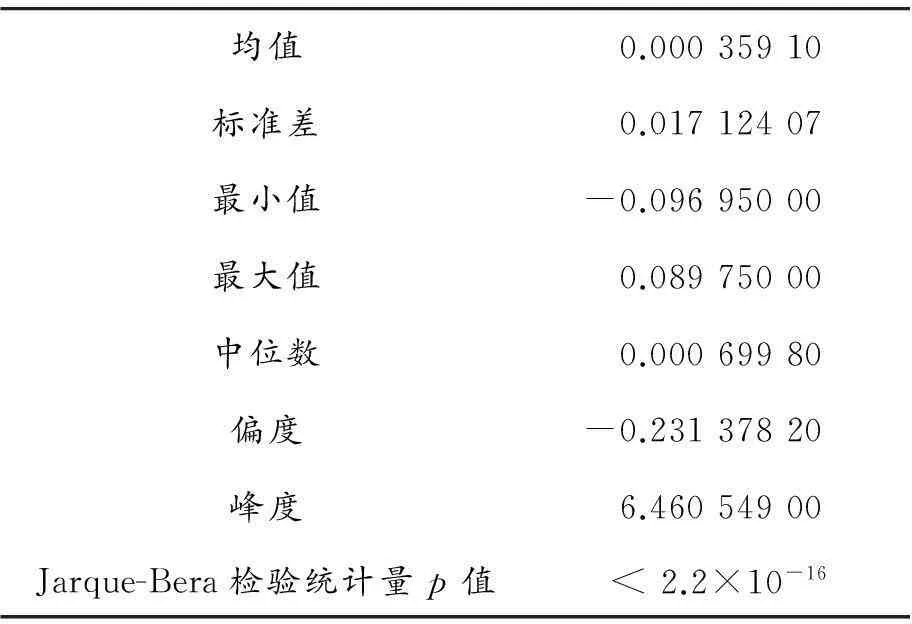
表1　沪深300指数日对数收益率序列的

3.2EGARCH模型拟合

从图2可以看出：日对数收益率的样本ACF的值均在两倍标准差之内，其序列相关性较弱；而平方收益率的样本ACF均超出两倍标准差，表现出较强的相关性，说明收益率序列存在非常显著的ARCH效应[8]。故在此用EGARCH(1,1)模型来拟合该数据。表2给出了EGARCH(1,1)模型的参数估计，其中括号内为估计的标准误差。

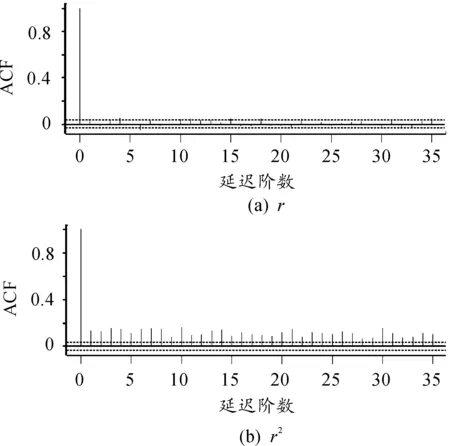
图2　沪深300指数日对数收益率序列和平方收益率序列的ACF图表2　EGARCH(1,1)模型的参数估计

μtωα1β1γ10.000132(0.000308)-0.92178(0.006589)-0.013694(0.010349)0.988046(0.000656)0.144162(0.019526)

图3上面为残差序列概率密度直方图，曲线则是与残差序列等均值、等方差的正态分布概率密度。图3下面是残差序列对正态分布的QQ图，以样本分位数为纵坐标、正态分位数为横坐标的点在两端偏离了斜率为1的直线，残差序列表现出明显的“尖峰厚尾”性。对其做Jarque-Bera正态性检验，检验统计量的p值小于2.2×10-16，拒绝了其正态性假设[14]。

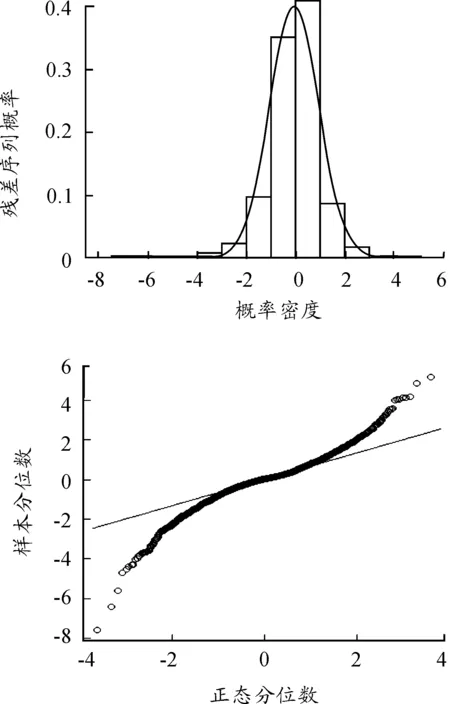
图3　修正残差序列概率密度函数及QQ图

在金融中最小收益率与持有多头金融头寸有关，所以一般将极值理论应用到给定时间的资产最小收益率上；又由于负的序列的最大值的相反数即为正的序列的最小值，所以利用变换-rt=-μt-at, -at=σt·(-εt)将极值理论应用至修正残差序列的负值而不是其本身。本文对极值理论的分析采用的是R软件中evir程序包。

3.3对修正残差序列拟合GPD

POT方法要求指定一个阈值u，阈值u的选择依赖于对象序列。经验表明：可以通过选择阈值u使得超越的次数大约为样本总数的5%[8]。由于本文的重点不在阈值的选取上，在此选用经典的超越量均值函数图选取阈值。当u大于某个阈值u0时，超越量均值函数关于u是线性的[15]。图 4给出了修正残差序列的超越量均值函数图，由图可知：阈值选1.5是比较合理的。

表3给出了负的修正残差序列在阈值选1.5时拟合GPD参数的极大似然估计。

图5是负的修正残差序列拟合GPD的诊断检验图，其中：(a)是超越量的分布函数图(横坐标取对数刻度);(b)是残差的碎石图；(c)为尾概率估计(取对数刻度);(d)为QQ图。结果表明：GPD很好地拟合了数据。

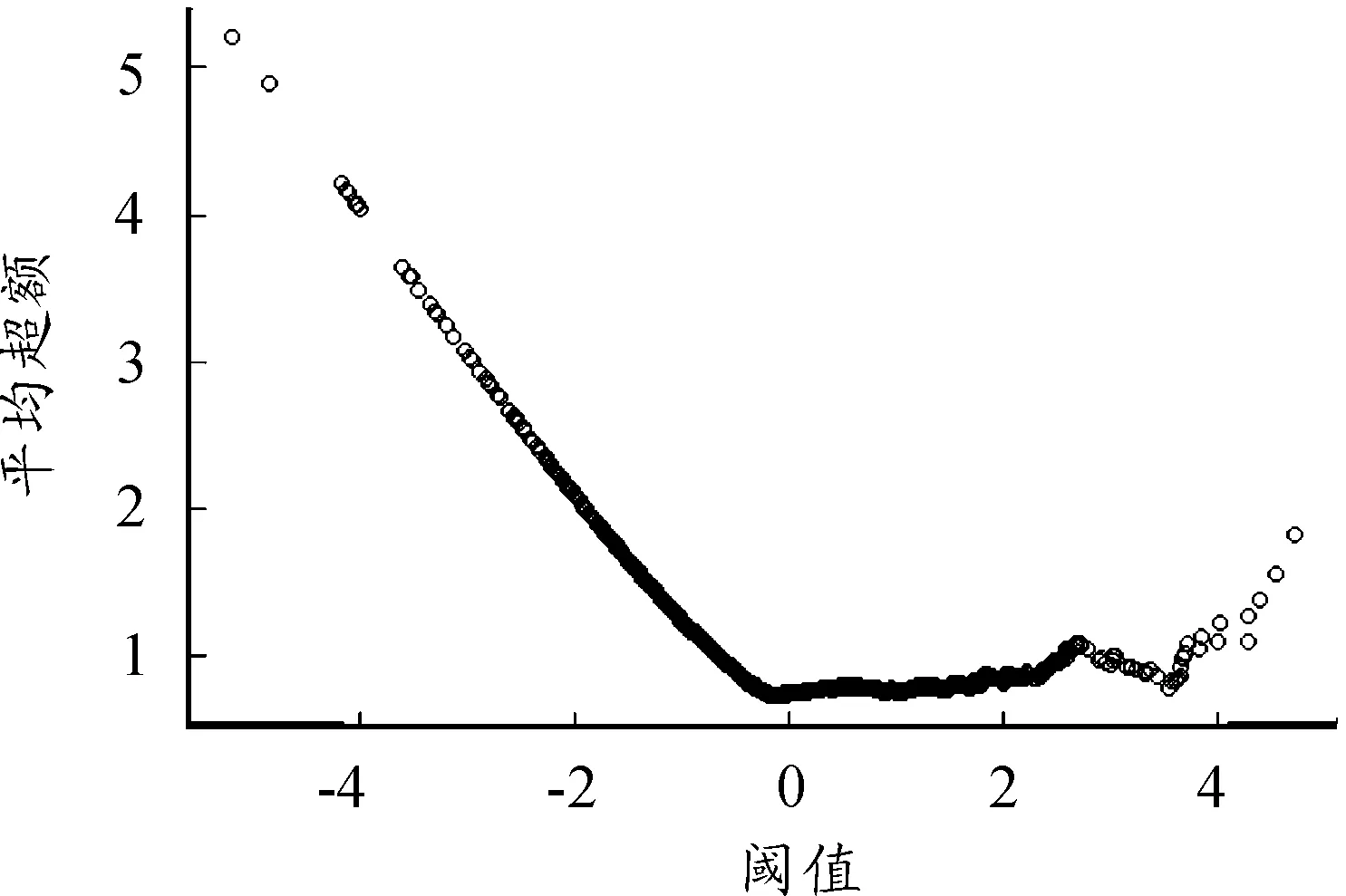
图4　负的修正残差序列超越量均值函数图表3　负的修正残差序列拟合GPD的参数估计

Nuξ^^σu=1.5205(约占样本总量的6.4%)-0.09688922(0.07712182)0.71142533(0.07387009)

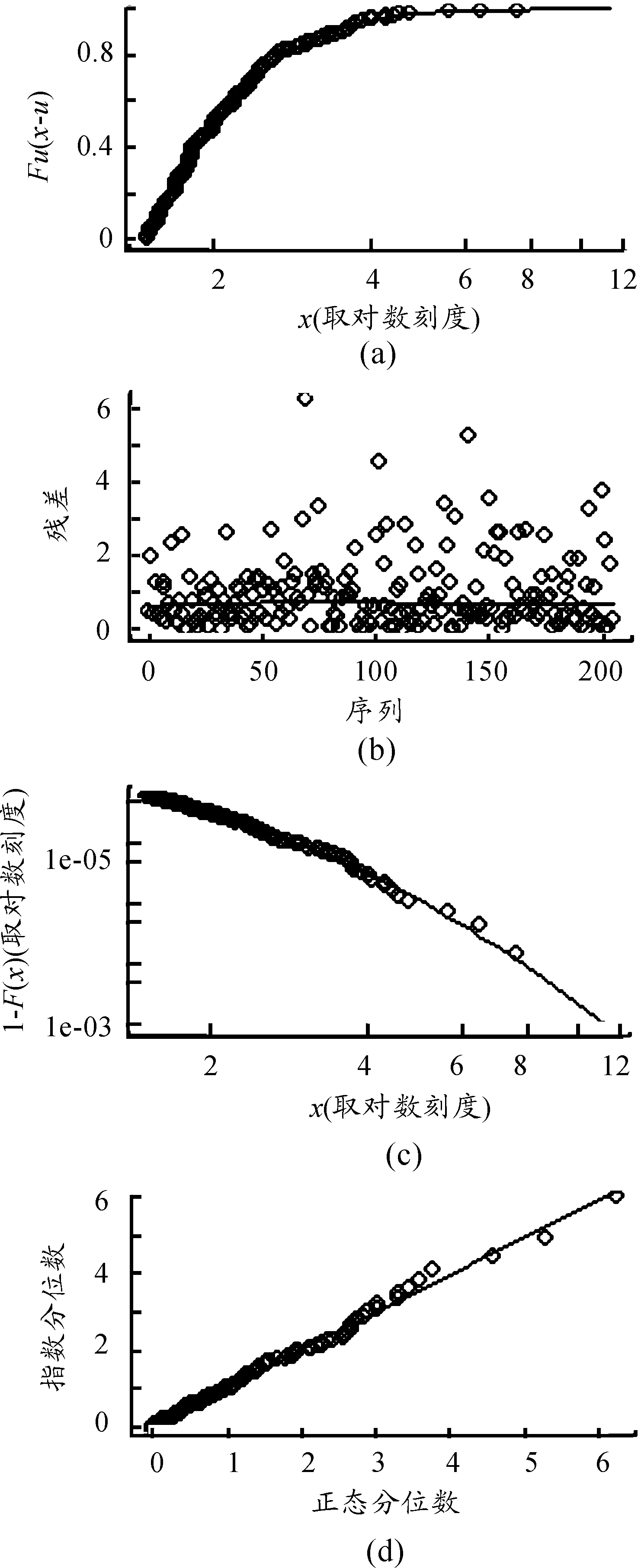
图5　负的修正残差序列拟合GPD的诊断检验

3.4VaR的返回测试

无论采用哪种方法得到收益率序列的VaR值，其实质都是一个估计值，这样就不可避免地存在误差，这些误差可能是由于模型的不充分、估计方法的缺陷或是随机误差造成的，所以要对其结果进行返回测试。VaR返回测试的方法很多，其中最常用的是文献[16]提出的失败率检验法。该方法是将观测到的收益率与计算的VaR进行比较，小于VaR的情形可以被看作一个二项分布中出现的独立事件。定义示性变量

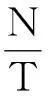
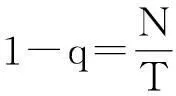
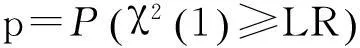
在此采用2014-01-02—2015-04-03共305天的数据对沪深300指数的日对数收益率进行返回测试。表4列出了两种模型的VaR返回测试结果，可见对修正残差序列采用极值理论得到的VaR在q=95%和q=99%的置信水平下均通过了检验，而传统的残差序列服从正态分布的模型在q=99%的置信水平下却没有通过检验。

图6和图7分别展示的是在q=95%和q=99%置信水平下对修正残差序列采用极值理论和正态分布拟合得到的VaR。可以看出：对残差序列直接采用正态分布拟合往往低估了风险，而对修正残差序列采用极值理论拟合GPD得到的VaR对风险的度量更准确。

表4　修正残差序列不同分布假设下收益率的VaR返回测试结果

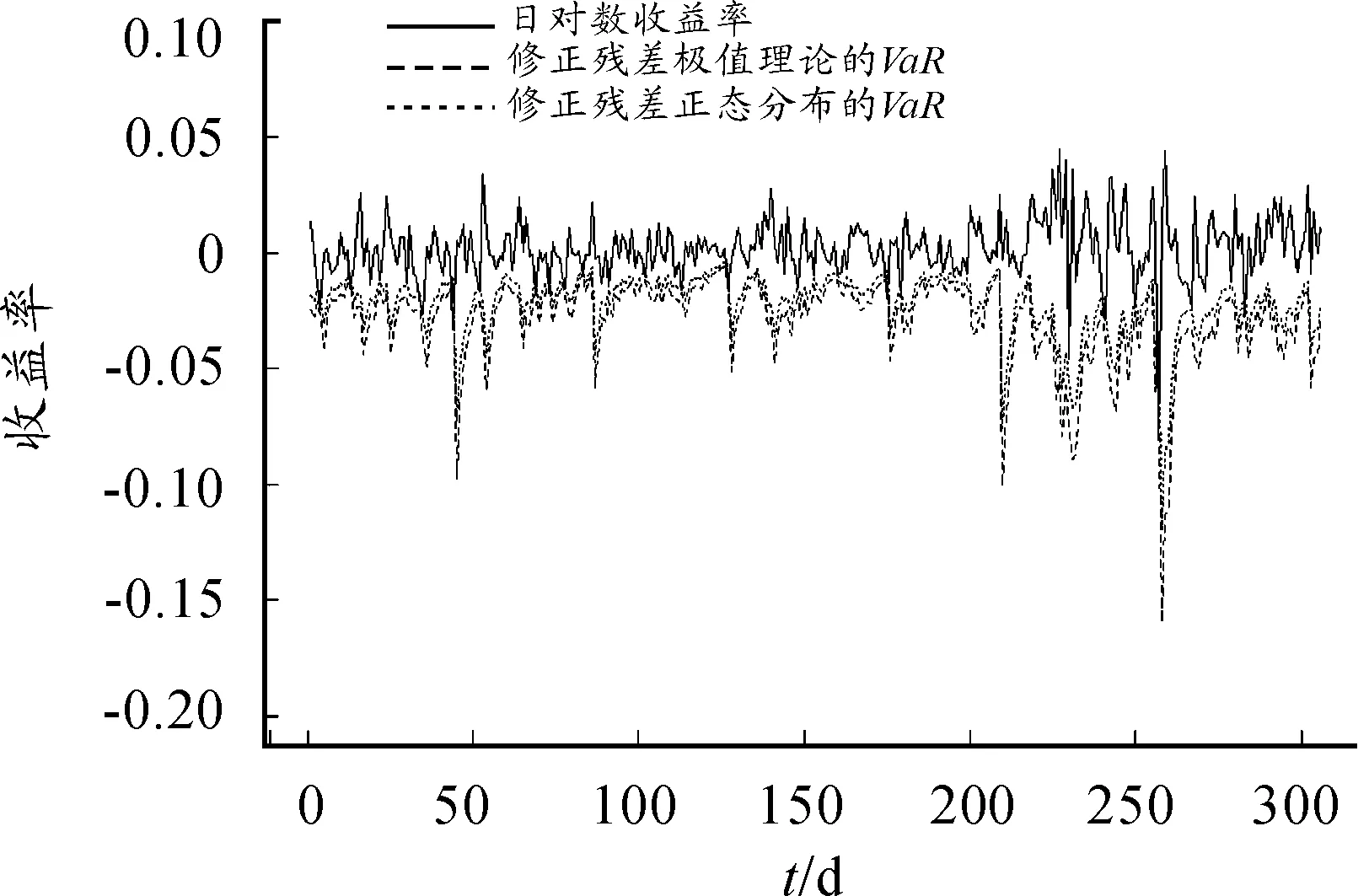
图6　q=95%置信水平下修正残差序列不同分布假设下的收益率的VaR

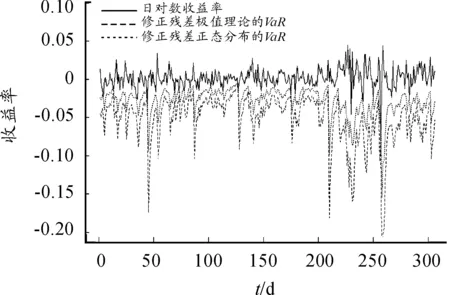
图7　q=99%置信水平下修正残差序列不同分布假设下的收益率的VaR

4结束语

本文在EGARCH模型的基础上，结合了极值理论的优点，构造出一种新的EGARCH-GPD模型，并将其应用于沪深300指数日收益率的VaR度量上体现了其波动率时变的特征和“杠杆效应”。基于广义Pareto分布的极值理论更有效地刻画了收益率序列“厚尾”的特点，在一定程度上提高了VaR的预测精度。

参考文献：

[1]张锐,魏宇,金炜东.基于MRS-EGARCH模型的沪深300指数波动预测[J].系统工程学报,2011,26(5):628-635.

[2]王博.基于ARMA-GARCH模型的上证指数实证分析[J].科学技术与工程,2012,12(5):1671-1815.

[3]DANIEL B N.Conditional Heteroskedasticity in Asset Return:A New Approach [J].Econometrica,1991,59(2):347-370.

[4]赵树然,任培民,赵昕.基于CARR-EVT整体方法的动态日VaR和CVaR模型研究[J].数量经济技术经济研究,2012( 11):130-148.

[5]俞慧琴.基于极值理论VaR模型的上市公司行业风险比较研究[D].杭州:浙江大学,2013.

[6]DANIELSSON J,CASPER G D V.Value-at-Risk and Extreme Returns [J].Annales d’Economie et de Statistique,2000,60:239-270.

[7]REISS R D,THOMAS M.Statistical Analysis of Extreme Values [M].Berlin:Birkhauser,2007.

[8]赵树然,任培民.极值理论在高频数据中的VaR和CVaR的风险价值研究[J].运筹与管理,2007,16(6):128-132.

[9]WANG H,PAN J G.Inspirations from Phylogeny of Market and Credit Risk Measurement Methods Which Benefit to Studies on Operational Risk Measurement International Conference on Engineering and Business Management.USA,2012.

[10]周孝华，张保帅，李强.基于SWARCH-GED模型的极值VaR度量[J].系统工程,2013,31(1):29-36.

[11]MCNEIL A J.Calculating quantile risk measure for financial time series using extreme value theory [J].ASTIN Bulletin,2000,27(1):117-137.

[12]ABHAY K S,DAVID E A,POWELL J R.Extreme market risk and extreme value theory [J].Mathematics and Computers in simulation,2013,94:310-328.

[13]孙丽娟.风险定量分析:损失模型及其在保险与金融风险管理中的应用[M].北京:北京大学出版社,2011.

[14]SMITH R L.Estimating tails of probability distribution [J].The Annals of Statistics,1987,15:1174-1207.

[15]RUEY S T.An Introduction to Analysis of Financial Data with R,First Edition [M].[S.l.]:John Wiley & Sons,2013.[16]PAUL H K.Techniques for Verifying the Accuracy of Risk Measurement Models[J].The Journal of Derivatives,1995,3(2):73-84.

(责任编辑刘舸)

VaR Forecasting for CSI 300 Index Based on EGARCH-GPD Model

WEI Zheng-yuan, LI Juan, LUO Yun-feng

(College of Mathematics and Statistics, Chongqing University of Technology,Chongqing 400054, China)

Abstract:This paper constructed a new EGARCH-GPD model combined the classical EGARCH model with extreme value theory based on generalized Pareto distribution, and provided the dynamic estimation problems of VaR. The results of VaR back testing on CSI 300 index show that compared with the EGARCH model based on normalized residual, the new model can effectively describe the time-varying volatility and the ‘fat tail’ of financial data, hence increase the prediction accuracy of VaR in a certain extent.

Key words:EGARCH model; generalized Pareto distribution; POT; VaR; Kupiec proportion of failures test

收稿日期：2015-09-22

基金项目：重庆市自然科学基金资助项目(cstc2012jjA00018)；重庆市教委科学技术研究项目(KJ130810)

作者简介：魏正元(1975—)，男，湖北襄阳人，博士，副教授，主要从事应用概率统计、金融统计、金融数学研究；李娟(1991—)，女，河南信阳人，硕士研究生，主要从事金融统计与数据分析相关研究。

doi:10.3969/j.issn.1674-8425(z).2016.05.021

中图分类号：O21

文献标识码：A

文章编号：1674-8425(2016)05-0119-06

引用格式：魏正元，李娟，罗云峰.基于EGARCH-GPD模型的沪深300指数的VaR度量[J].重庆理工大学学报(自然科学)，2016(5):119-124.

Citation format：WEI Zheng-yuan, LI Juan, LUO Yun-feng.VaR Forecasting for CSI 300 Index Based on EGARCH-GPD Model [J].Journal of Chongqing University of Technology(Natural Science)，2016(5):119-124.