三相电压型PWM整流器的建模方法

李明辉,贾文超,谢世康

(长春工业大学 电气与电子工程学院,吉林 长春　130012)



三相电压型PWM整流器的建模方法

李明辉,贾文超,谢世康

(长春工业大学 电气与电子工程学院,吉林 长春130012)

摘要整流器模型建立直接影响控制策略,通常系统采用基尔霍夫定律和拉格朗日方程建立数学模型,其状态变量间存在耦合。文中针对开关函数描述的数学模型为非线性且控制器设计困难的特征,采用开关周期平均法建立系统平均模型,分离扰动得到稳态模型和线性时不变的小信号模型。结果表明,小信号模型较传统模型更有利系统控制器的设计。

关键词PWM整流器;开关函数;非最小相位;小信号模型

谐波和无功功率已成为电网的两大公害,绝大多数变流器的前端电路是整流器,整流器的工作状态直接影响电网的谐波和无功功率的大小。所以,整流器的谐波抑制和功率因数提高问题是治理电网污染的重点[1-6]。由于三相PWM整流器开关模型的非线性,时变性给电压外环和电流内环控制器的设计带来了较大不便,系统控制策略直接影响系统的动静态性能及鲁棒性[7]。

本文在理论分析的基础上,采用3种方法对三相电压型PWM整流器进行建模。首先采用基尔霍夫定律和拉格朗日方程建立系统数学模型。系统的数学模型普遍存在“负调现象”[6],对非最小相位系统进行研究,然后采用开关平均周期法建立PWM整流器的开关平均模型,再通过分离稳态分量和小信号扰动量分别得到稳态模型和两相旋转坐标下的相电压和相电流的解耦线性化动态小信号模型。此模型为非最小相位系统模型[7-11]。

1基于基尔霍夫定律的数学模型

图1　三相电压型PWM整流器拓扑结构图

定义开关函数[2-3]

(1)

根据基尔霍夫定律网测三相回路有[8-9]

(2)

对输出直流电压正极节点有

(3)

整流器网测电压三相对称[4]

(4)

2基于拉格朗日方程的数学模型

分析力学通过选择广义坐标作为描述质点系运动的变量,通过数学分析,从系统能量的角度出发来研究具体的力学问题。分析力学广泛应用在一些复杂多变量系统中,其重要理论工具就是拉格朗日方程。

选择广义坐标:设网侧电感的电荷量分别为qLa,qLb,qLc;直流侧电容电荷量为qo。由拉格朗日方程[6]

(5)

(6)

系统磁场能量为

(7)

系统电场能量为

(8)

系统耗散能量函数为

(9)

以ia,ib,ic,uo为状态变量,两种理论建立数学模型得到相同的数学模型。

三相静止abc坐标系中的数学模型如下

(10)

两相旋转dq坐标系下的数学模型为

(11)

3基于小信号理论的数学模型

3.1三相PWM整流器的非最小相位特性

非最小相位系统的开环传递函数中含有不稳定环节或延迟环节,系统有位于s右半开平面上的极点或零点。最小相位特性的研究可分析出“负调现象”产生的原因,确定PWM整流器控制系统的结构,有利于控制方法的研究。由于开关函数描述的数学模型为非线性模型,控制器设计困难。所以,本文利用开关周期平均法建立系统平均模型[11],推导其传递函数,研究其非最小相位特性。

3.2基于小信号理论建立数学模型

系统建模做如下假设[7]:(1)开关为理想器件,忽略开关的死区时间,忽略电感、电容的内阻;(2)电路中变量的交流分量的幅值必须远小于相应的直流分量[11]。在一个开关周期内电感电流平均值和电容电压平均值及开关函数平均状态量定义如下

(12)

得到三相PWM整流器在三相静止abc坐标系下的数学模型如式(10)所示。

由开关函数关系得到:在一个开关周期内,电感电流平均值、电容电压平均值及开关函数平均状态量定义为直流量和扰动小信号交流量[6]。表示为;ID=ID+ΔID;Iq=Iq+ΔIq;uo=uo+Δuo;sD=sD+ΔsD;sq=sq+Δsq。将直流分量代入式(2),求得静态工作点为

(13)

忽略电网电动势扰动和网侧等效电阻,将扰动量代入式(10)可得小信号数学模型为

(14)

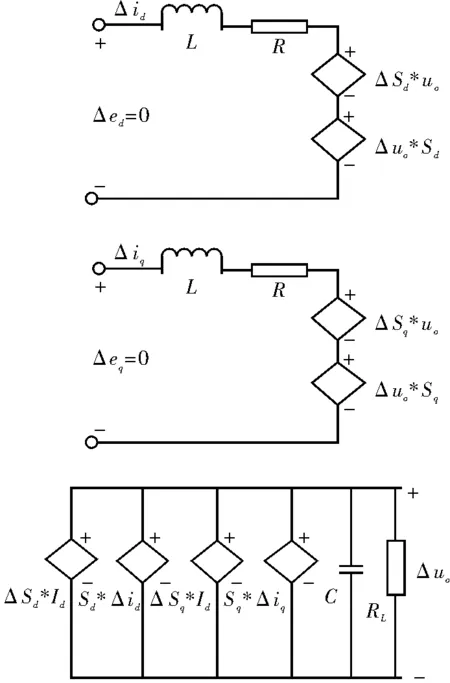
图2　解耦后小信号模型等效电路

由于稳态Iq=0时,并对式(14)进行拉氏变换,可得

(15)

输入对于d轴电流输出传递函数为

(16)

传递函数的零点在s平面左半平面,输入对于d轴电流输出是最小相位。输入对于直流电压输出传递函数为

(17)

稳态下即为输入对于直流电压输出的非最小相位系统。

经解耦后三相电压型PWM整流器小信号模型等效为两个并联的DC/DC升压变换器。电流环路的设计可按单输入单输出系统设计,给控制器的设计带来了便利[7]。

4结束语

在传统的基尔霍夫定律和拉格朗日方程的基础上,采用小信号理论对三相PWM整流器进行建模,更好的掌握系统特性,便于实现对系统的更好控制。

参考文献

[1]张晓华,郭博源,周鑫,等.PWM整流器的欠驱动特性与非线性控制[j].中国电机工程学报,2011,31(33):85-92.

[2]张卫平.开关变换器的建模与控制[M].北京:中国电力出版社,2006.

[3]王兆安,刘进军.电力电子技术[M].5版.北京:机械业出版社,2009.

[4]张兴,张崇魏.PWM整流器及其控制[M].北京:机械工业出版社,2012.

[5]Zhou k L,Wang D w.Relationship between spacevector modulation and three-phase carrier-based PWM:a comprehensive analysis[j].IEEE Transactions on Industrial Electronics,2002,49(1):186-196.

[6]张卫杰.欠驱动三相电压型PWM整流器控制系统研究[D].哈尔滨:哈尔滨工业大学,2007.

[7]瞿博,吕征宇.三相电压型PWM整流器小信号建模及其控制器设计[j].电工技术学报,2010(5):103-108.

[8]张涛.电力电子变换器中滑模变结构控制技术研究[D].杭州:浙江大学,2006.

[9]陈雄春.基于滑模变结构三相PWM整流器内模控制[D].湘潭:湘潭大学,2014.

[10]岳晖.基于滑模变结构控制的电压型PWM整流器的研究与实现[D].沈阳:东北大学,2011.

[11]夏加宽,徐纯科,黄伟.三相PWM整流器的小信号建模及其双闭环控制[j].电气技术,2009(11):41-44.

Three-phase Voltage PWM Rectifier’s Modeling Method

LI Minghui,JIA Wenchao,XIE Shikang

(Institute of Electrical and Electronic Engineering,Changchun University of Technology,Changchun 130012,China)

AbstractThree-phase PWM rectifier is widely used because of low input current harmonics and high power factor.The construction of system model is an important part of research,and the establishment of the rectifier model has a direct impact on the control strategy.Kirchhoff’s law and the Lagrange equation are usually adopted to establish the mathematical model with coupling between variables.Since the mathematical model described by switching function is nonlinear and the controller’s design is difficult,the average model of switch cycle average method is adopted to establish the system to get the steady-state model and a small signal model of linear and invariant.The results show that the small signal model is better in system controller design than the traditional model.

KeywordsPWM rectifier;switching function;non-minimum phase;small-signal model

doi:10.16180/j.cnki.issn1007-7820.2016.05.032

收稿日期:2015-10-02

作者简介:李明辉(1990—),男,硕士研究生。研究方向:电力变换。贾文超(1965—),男,教授,硕士生导师。研究方向:电力变换等。

中图分类号TM461

文献标识码A

文章编号1007-7820(2016)05-121-03