丢包博弈之谜：对互惠理论的挑战

赵玉亮（南开大学滨海学院，天津，300270）



丢包博弈之谜：对互惠理论的挑战

赵玉亮
（南开大学滨海学院，天津，300270）

［摘要］互惠理论是近几十年行为经济学和实验经济学的主要研究内容之一，而Dufwenberg 和Gneezy 在2000年提出的丢包博弈的实验表明，丢包人的回报行为与捡包人放弃的外部选择权的大小并不存在正相关关系。Servátka、Vadovi （2009）和Cox等（2010）分别尝试用外部选择权的不平等和外部选择权对丢包人的凸显性来破解丢包博弈之谜，他们的实验仍然没有改变丢包人的决策行为与捡包人放弃的外部选择的不对称性，丢包博弈仍旧是个悬而未决的谜。破解丢包博弈之谜，对探究当前我国市场经济条件下企业的竞争与合作、多成员之间的团队创新行为有重要的启示意义。

［关键词］丢包博弈之谜； 互惠理论； 外部选择权的不平等； 外部选择权的凸显性

自古以来互惠就是人类交往的基本的行为规范之一，我国传统文化中即有“受人滴水之恩，定当涌泉相报”的思想，衔环结草、以恩报德的典故更是不胜枚举。亚当斯密在其《道德情操论》中多次提到“善以善报”的思想①其中《道德情操论》第6卷第2章提及“ Kindness is the parents of kindness”。。现实生活中，人们不但经常对那些善意的行为进行回报，而且还经常牺牲自己的利益惩罚那些行为不善的人，Rabin（1993）将前一种行为称为正互惠（positive reciprocity），将后一种行为称为负互惠（negative reciprocity）。正互惠和负互惠在产业内企业间的竞争和合作行为、行业协会以及多成员的团队创新中也广泛存在，基于声誉、激励和惩罚层面的管理机制的存在显著地提高了产业的合作水平和团队绩效。

近年来，行为经济学和实验经济学也开始着重研究现实场景和实验市场中的互惠现象，并将互惠现象模型化，受互惠激励的人们在交往中可能产生完全不同于基于纯自利人行为模型预测的结果（Rabin，1993 ；Fehr and Schmidt ，1999 ；Bolton and Ockenfels，2000 ；Charness and Rabin，2002；李晓义和李建标，2009）。部分学者对强互惠行为的证据、生物基础和演化的现有文献进行了评述（韦倩，2010）。

一、互惠理论：不同博弈模型中的互惠现象

实验经济学家和行为经济学家在最后通牒博弈、信任博弈、偷袭者博弈和礼物交换博弈中发现，互惠偏好显著影响着实验室中被试的行为。

1．最后通牒博弈实验

Guth等（1982）开创性地实验了最后通牒博弈。实验中将被试随机分为提议者和回应者，实验者提供一定数量的金钱由提议者分配，如果回应者同意提议者的分配方案，则按照其方案分配，如果不同意其方案，则双方什么都得不到。在他们的实验数据中，提议者愿意分给对方的比例大都在30%-50%之间，低于20%的分配比例以很高的概率被拒绝。回应者愿意放弃一个正的分配额来惩罚提议者，表现出强烈的负互惠倾向。世界各地众多不同形式的最后通牒博弈结果为负互惠行为提供了强有力的证据。为了回应“赌注盘”（stake cake，即提议者和回应者分配的金钱总数）变大以后拒绝率就会明显下降的质疑，Cameron（1995）在印度尼西亚实施的最后通牒博弈实验中将赌注盘变为相当于实验参与者三个月的日常消费②Cameron 在印度尼西亚实施的实验中最大赌注盘为200000印尼盾，实验问卷显示，该数额为实验参与人三个月的日常消费。，结果证明回应者的拒绝率和低赌注盘时的拒绝率并无明显差异。Hoffman、Mc Cabe和Smith（1996）发现赌注盘为10美元和100美元时提议者的分配方案和回应者的拒绝率无显著差异，而产权的配属③即博弈参与人提议者和回应者角色的通过何种方式确定。却对提议者分配分布和回应者的拒绝行为有显著影响。李建标、庞荣辉（2010）的三人最后通牒博弈数据也表现出该特点，在产权不清晰的重复三人最后通牒实验下拒绝率为17.3%；而在产权清晰的实验下，拒绝率为4.9%。为回应大学生被试由于类似的社会文化背景而使得最后通牒博弈实验结果缺乏普适性的质疑，Henrich等（2001）展开了最后通牒博弈的跨越五大洲和12个国家的跨文化调查，被试涵盖了15个不同文化背景的社会团体，这些社会团体包括狩猎社会、游牧社会、迁徙农耕社会和定居农耕社会，赌注盘大约为当地所在社会1-2天的工资水平。尽管这些不同背景的社会表现出来的行为差异很大，但提议者分给对方的比例在26%-68%之间，当分给对方的比例低于20%时，拒绝的概率在0.4-0.6之间。最后通牒博弈实验中回应者对正的分配额的拒绝反映了人类交往中的负互惠现象，人们愿意放弃唾手可得的收益来惩罚他们认为不公的分配结果。

2． 信任博弈实验

Berg（1995）设计了一个投资环境下的两阶段信任博弈来研究信任与互惠问题。该博弈执行如下：第一阶段，被试随机分为A类型和B类型，A类型参与人和B类型参与人分别得到10美元初始禀赋，A类型参与人需要决策将其10美元中的多少分给与之匹配的匿名的B类型参与人，该数值记为Ma（0≤Ma≤10，Ma，但是该数值被乘以3倍以后给予B类型参与人；第二阶段，B类型参与人得到3Ma，并且需要决定返还多少给A类型参与人，返还的数值记为kb（0≤kb≤30，kb），A类型参与人收益为：Pa=10- Ma+kb，B类型参与人收益为：Pb=10+3Ma-kb。根据子博弈精炼纳什均衡，B类型参与人的占优策略是（kb= 0），A类型参与人预期到B类型参与人的选择，因此A类型参与人选择Ma= 0，因此单次匿名交往的博弈实验中该博弈的均衡结果为（Ma= 0，kb= 0。）。然而，事实上，他们的实验结果表明，A类型参与人和B类型参与人的选择显著不为0，并且二者高度相关。在Berg教授以后，世界各地实施的诸多信任博弈实验④Cox的三合一实验分别为标准的信任博弈实验和两个拓展三倍的独裁者博弈（一个为增值三倍的独裁者博弈，一个为调整禀赋的标准独裁者博弈）。都从不同的角度证明了该结论。Cox（2004）设计了三合一的信任博弈实验识别信任和互惠行为，其信任博弈中81%（26/32）的A类型参与人选择了大于零的Ma，53%（17/32）的B类型参与人选择了大于零的kb，增值三倍的独裁者博弈中，63%的A类型参与人选择了正的Ma。夏纪军（2005）利用Cox（2004）的框架，测度了基于20名中国被试的人际间的信任水平和可信水平，其中基础信任博弈实验中A类参与人选择的Ma均值为5.24，而B类参与人选择的kb均值为8.5。陈叶烽（2009）将信任博弈中社会偏好行为进行了分解，得出了信任博弈中A类型参与人的决策行为受互惠偏好的显著影响、B类型参与人的回报行为受互惠偏好和利他偏好的显著影响的结论。尽管学者们得出的信任博弈中参与人的行为受互惠偏好和利他偏好的影响程度不同，但都证明了互惠现象的广泛存在。

3． 偷袭者博弈实验

Abbink、Irlenbusch和 Renner（2000）（以下简称AIR）提出的偷袭者博弈（moonlighting game）本质上是信任博弈的扩展，允许参与人可以采取正互惠和负互惠两方面的行动。参与人A和参与人B随机配对，在两阶段博弈开始前，双方账户中都被赋予12单位代币的初始禀赋。第一阶段，参与人A选择一个行动a（-6≤a≤6），如果a≥0，则A账户减少a单位代币，而B账户增加3a单位代币；如果A选择的a＜0，则A账户中增加单位代币，而B账户中减少a单位代币。第二个阶段B观察到A的行动后，选择一个行动b，如果b≥0，则A账户中增加b单位代币，而B账户中减少b代币，如果b≤0，则A账户中减少3单位代币，而B账户中减少b单位代币。偷袭者博弈的一个显著特征就是参与人A可以选择给予也可以选择拿走，而参与人B可以根据第一阶段A的行动进行奖励或者惩罚。AIR的实验结果表明，参与人B对A选择拿走的行动（a＜0）实施了惩罚，而且拿走的多少与实施的惩罚（b＜0）程度显著正相关。Falk、Fehr 和Fischbacher（2008）在偷袭者博弈的框架中设计了两种设置：动机设置（Intention Treatment）和非动机设置（Non-intention Treatment），动机设置中参与人A自主选择a，a的选择完全在参与人A的自主控制中，而非动机设置中，通过主持人在参与人B面前掷骰子决定a。他们的实验结果表明公平动机发挥着重要的作用，传统经济理论中仅将结果放入效用函数中是值得怀疑的，仅考虑分配结果的公平模型（如Bolton and Ockenfels，2000；Fehr and Schmidt ，1999）而忽略了非结果因素对互惠公平的影响，某种程度上是不完全的。Engelmann和Strobel（2010）在偷袭者博弈中改变了参与人A和参与人B的初始禀赋来考察偷袭者博弈的不平等厌恶和互惠对参与人行为的影响，在设置1中将参与人A和参与人B的初始禀赋分别设为17和18，而设置2中的参与人A和参与人B的初始禀赋分别设为17和48。以往的实验表明，当不平等厌恶与互惠一致时，不平等厌恶理论解释良好；当不平等厌恶与互惠矛盾时，不平等厌恶几乎失去了解释力。面对参与人A相同的行动，互惠的参与人B在两种设置下的行为应该没有差异，而不平等厌恶的参与人应该反应不同。参与人B的实验结果在两种设置下区别并不明显。与不平等厌恶理论相比，显然，在他们的实验中参与人B的行为受互惠理论指导更强烈。

4． 礼物交换博弈实验

学者们经常讨论礼物交换博弈（gift exchange game）中的互惠现象，并用来解释现实中经济学经典范式失灵的预测。“礼物交换”是阿克洛夫最先在研究劳动契约制度时提出的，他认为劳动契约制度类似于不完全的“礼物交换”，工资决定了工人的努力水平规范，并反过来影响努力水平规范；企业提供一个高于市场出清水平的工资的原因就是“礼物交换规范”（Gift Exchange Norm）的存在，工人公平导向的行为导致了非自愿失业的存在（Akerlof，1982；Akerlof and Yellen，1988，1990）。Fehr、Kirchsteiger和Riedl（1993）在实验中刻画了阿克洛夫描述的情境，检验了公平对市场价格的影响。买者（雇主）提出价格，通过单向口头拍卖决定价格，卖者（雇员）同意某个买者的价格后决定提供商品的质量，商品的质量决定了卖者的收益，同时卖者的成本会随着提供商品质量的提高而增加。实验结果表明，买者要约价格远远高于市场出清的价格水平，以此期待卖者提供高质量的商品回应高于市场出清的价格。结果表明，卖者的提供质量与买者要约的价格正相关，因此实验结果对阿克洛夫的非自愿失业的公平工资——努力理论（wage-effort theory）提供了实验支持。Fehr、Gachter和 Kirchsteiger（1997）对“礼物交换”博弈中的互惠行为进行更为细致的刻画。人们对善意的行为进行回报和对恶意行为进行惩罚的正负互惠行为有助于契约的实施，并且能够增加交易双方的效率。如果市场能够为交易双方提供互惠的机会，就会产生稳健和强有势的互惠效应，因此能够增大可实施的行动集，产生大量的交易利得。在他们的实验中给出了两个主要设置：弱互惠设置WRT（weak reciprocity treatment） 和强互惠设置SRT（strong reciprocity treatment）。弱互惠设置中仅有雇员有机会实施互惠行为，而强互惠设置中交易双方都有机会进行互惠反应。“礼物交换”博弈中SRT设置进行三阶段博弈，WRT仅进行前两阶段的博弈。第一阶段，雇主提出契约要（w，f），其中w 为工资，为要求的努力水平，f为偷懒的罚金，雇员被通知所有的雇主劳动契约要约以后，随机选择契约，契约达成；第二阶段，同意雇主要约的雇员选择努力水平e偷懒（即e＜）有概率s（0＜s＜1）被第三方发现，该情况下雇员必须支付罚金f给雇主。因此，雇员不偷懒的期望效用是uns= w-c（e），c（e）为雇员努力的成本，且c′（e）＞0，c（0）= 0，雇员偷懒的期望效用为us=（1- s）［w-c（e）］+ s［w-c（e）- f］。如果与之交易的雇员未偷懒或者偷懒没有被发现则雇主的收益为π=（q-w，q为外生给定的赎回价值，如果其雇员偷懒并且被发现则其收益为π=（q-w+ f；第三阶段，雇主实施互惠行为阶段，雇主观察到雇员的努力水平后，选择一个数值p（p∈［0，2］），雇员在前两个阶段的收益乘以p ，p＜0和p＞0都会导致雇主的成本k（p），k（p）在区间p∈（0，1）递减，在区间p∈（1，2）递增，k（1）= 0，不偷懒或者偷懒未被发现的雇员的收益为uns=［w-c（e）］p ，其雇主的收益为π=（q-w-k（p）；偷懒且被发现的雇员的收益为us=［w-c（e）- f］p ，其雇主的收益为π=（q-w+ f-k（p）。显然，自利的雇主会选择p=1，否则都会导致其成本的增加。自利如果作为共同知识，理性的雇员预期到雇主的选择，第三阶段的存在并不影响其努力行为的选择。他们的实验数据表明WRT下存在非明显的互惠反应，而SRT下互惠反应非常强烈，尽管雇主要求了更高的努力水平，而偷懒的概率显著下降，交易双方的收益都有所增加。互惠作为某种契约实施手段显著增大了可实施的交易空间，提高了交易效率。

二、丢包博弈之谜

丢包博弈是Dufwenberg 和Gneezy（2000）（下文简称DG）提出的，他们假设了如下场景：一个人在大街上发现了一个钱包，而且没有人发现他捡到了钱包，钱包中有现金和证件等物品，显然现金对其有效用而证件对其没有实际的价值，对于钱包主人而言二者都是有价值的。捡包人可以选择将钱包拿到附近的派出所登记姓名等待钱包主人前来寻找，失主会给予一定的报酬，捡包者也可以将钱包据为己有。将该情形刻画成博弈模型如图1所示，第一时点上参与人1（捡包人）有两个选择：将总价值为20的包“归还失主”或者“据为己有”。如果选择“据为己有”则参与人1获得钱包中的现金收益x（0＜x＜20，x为外生给定的固定值），参与人2（丢包人）的收益为0；如果参与人1选择将钱包“归还失主”，则由参与人2决定如何分配20单位的总价值，参与人2分给参与人1的值记为y（0≤y≤20），则参与人1和参与人2的收益分别为y和20-y。参与人2行动的子博弈实际上是一个独裁者博弈。

如果参与人仅受个人物质收益激励，并且自利作为共同知识，则博弈均衡为（据为己有，0），因为参与人1预期到参与人2会最大化其物质收益20-y，选择y=0，所以参与人1在第一时点上选择“据为己有”，双方的收益是分别是x和0。然而该均衡是无效率的，如果参与人1选择归还失主，则双方的收益之和为20，大于在其选择“据为己有”下的双方收益之和x。同时，该博弈存在帕累托改进的空间，因为只要参与人2选y≥x，双方的福利都会有所改进。很多实验表明，人们在交往过程中可能受到很多其他非物质因素的激励，这可能减少了无效率的产生。根据互惠理论，参与人1可能放弃潜在收益x向参与人2表示友好，而参与人2会根据参与人1行为做出相应的互惠反应。

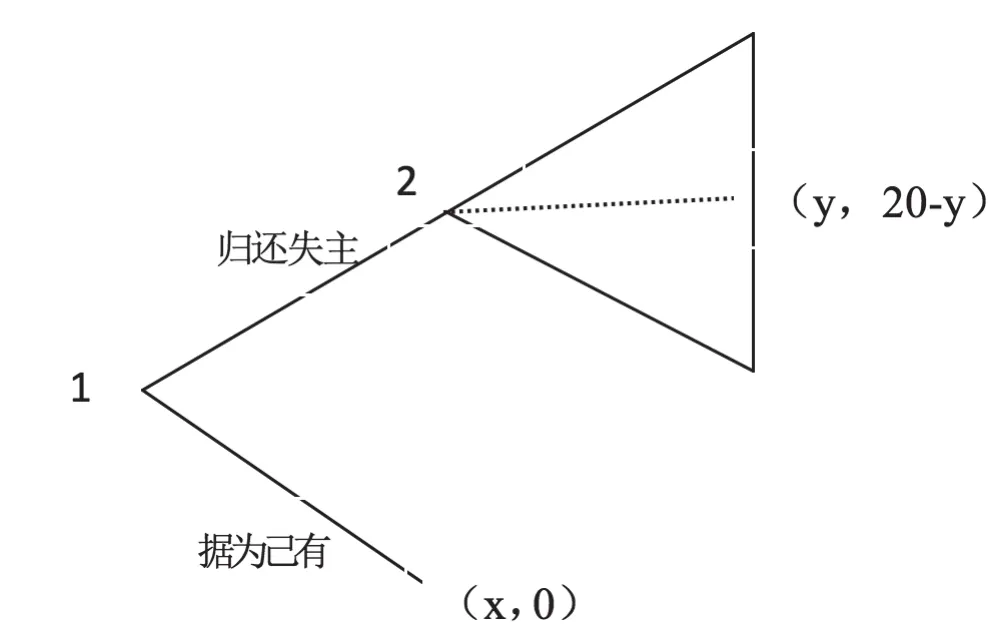
图1　DG的丢包博弈

DG（2000）的实验共进行了五局（sessions），每局实验中x分别设定为4、7、10、13、16，每局实验12组被试，对于参与人2实施了策略方法（strategy method）⑤越来越多的实验经济学家利用策略方法来诱导实验室和现实场景中的选择行为，让被试在他面临的每一个状态依赖的决策节点上做出选择，然后匹配被试，最后根据实现的节点来确定决策，忽略未实现的节点。，即参与人2在不知道参与人1选择的条件下做出选择y。为了检验互惠效应，同时他们还实施了两局独裁者博弈，将独裁者的选择行为与丢包博弈中参与人2的行为进行对比，如果存在互惠效应，则参与人2会比如果他（她）作为独裁者博弈中的独裁者给出更高的y值。同时为了测度信念对决策行为的影响，两位学者还测度了参与人1对参与人2分配给其的y值的猜测，同时令参与人2猜测了参与人1对y值的猜测值，并根据他们的猜测的精确度进行了支付。

丢包博弈实验结果表明，参与人1的行为明显与自利模型的预测不相符，在x=4、x=7、x=10、x=13、x=16的实验中，选择“归还失主”的被试的比例分别为100%、50%、66.7%、33.3%和8.3%，即使某些参与人1猜测参与人2返还给他的y值小于x。显然，随着表示友好的参与约束增大，愿意表示友好的被试者越来越少。参与人2的行为明显与互惠模型的预测不同，在x=4、x=7、x=10、x=13、x=16设置下的各局实验中，参与人2选择的y值平均值分别为7.33、4.83、7.54、6.12、5.75，检验结果也表明在5%的显著水平上无法拒绝x与y不相关的假设，而y却与参与人2对参与人1预期（即猜测）的预期正相关。更令人惊讶的是，在两局独裁者博弈实验中，独裁者选择的y值平均值为6.08，与丢包博弈中选择的y值并无显著区别，而独裁者博弈实验中，独裁者选择的y值与其对参与人1预期的预期也存在正向关系。DG（2000）给出的解释是参与人2（或者独裁者）不想让参与人1失望而不愿意给予参与人1低于其期望值的y值。

图2　Brandts、Guth和Stiehler的丢包博弈实验结构

Brandts、Guth和Stiehler（2006）（以下简称BGS）在研究指定分配权力的激励效应时实施了一个加入除捡包人⑥在Chaness、Haruvy和Sonsino（2007）称为先行动者（first mover），即图2中的X。和丢包人⑦在Chaness、Haruvy和Sonsino（2007）称为后行动者（second mover），即图2中的Y或Z。之外的第三方的三人丢包博弈实验。其实验结构如图2所示。三人共享一个总价值最大为12单位代币的“包”。首先，X决定选择外部选择权（即图2中的O）或选择让Y（或Z）来分配，三人共享该“包”（即图2中的D）。如果X选择外部选择权，则他的收益为x=3（6），Y和Z的收益则为0；如果X选择D即意味着他放弃了外部选择权，则由Y或Z来在三人之间分配总价值为12单位的代币，三人收益均为非负整数，且三人收益之和为12。为了考察分配权力对激励效应的影响，BGS设计了两种设置：X指定分配者的SA（selected allocator）设置和随机选择分配者的RA（random allocator）设置。在SA设置中，X决定他是否愿意放弃外部选择权和愿意让Y或Z作为分配者；RA设置中，如果X放弃外部选择权，则随机确定Y或Z作为分配者，二人被选为分配者的概率均为1/2。

受DG模型的鼓舞和直觉的影响，BGS的设置在考察分配者选择方式对分配结果影响的同时也考察了外部选择权大小对分配结果的影响。在其2（treatments）x3（sessions）x15（participants）的实验中，每局三个回合（rounds），前两回合中参与人X选择外部选择权收益为x=3，第三回合中X的外部选择收益为x=6。他们假定分配者会在外部选择权较大时（x=6）为自己保留的份额越小，因为不同的外部选择权收益意味着参与人X放弃的潜在收益的大小。实验结果表明他们的假设未被支持，高的外部选择权并不能使得分配者给予自己较低的份额。他们认为可能是不平等的外部选择权导致了违反直觉的结果，在两种外部选择权设置中，所有的收益全部给了参与人X。此外，两种外部选择权情况下的总收益也远远小于12，两种情况下参与人X放弃的外部选择权可能被视为一种义务而不是慷慨行为，因此不影响分配者后续的行为。

Chaness、Haruvy和Sonsino（2007）使用策略方法分别在三个大陆的互联网上、以色列和西班牙实验教室和美国的两个州（田纳西州和加利福尼亚州）的电脑机房实施了丢包博弈实验⑧Chaness、Haruvy和Sonsino（2007）的实验结构与DG基本类似，包对捡包人的价值x是从0，10，20，…，100中随机抽取的，而丢包人需要在假定捡包人归还包的情况下对于x的每个可能的值都做出一个具体的选择y，y∈（0，100）。，以考察社会距离对互惠的影响。尽管他们得出结论“很多参与人关心其他人的收益，即使他们是身在异国的陌路人，将近30%的网络参与人2选择的y与参与人1放弃的x正相关”，而事实上，在网络实验中，对于参与人1放弃的不同水平的x，高达48%的参与人2选择了固定的y值（36%的被试选择y=0，13%的被试选择y=50，9%的被试选择其他的固定值）。在实验教室和两州的电脑机房实验中选择固定y值的被试也分别高达35%和40%。在互联网、实验教室和两州的电脑机房实验中参与人2选择的y与x弱正相关的比例分别为28%、43%和33%。

到底是什么原因使得丢包博弈中的丢包人的回报行为与捡包人的放弃的外部选择权x的大小不存在正向关系或存在微弱的正向关系？是不平等的外部选择权，还是外部选择权对参与人2不够凸显？

三、外部选择权的不平等与丢包博弈之谜

为了检验是否是BGS提出的不平等的外部选择权可能导致丢包博弈之谜的猜想，Servátka和Vadovi （2009）实验比较了被试在平等和不平等的外部选择权条件下的行为。其实验结构如图3所示。如果参与人1选择归还（即图3中的IN），则参与人2可以在其和参与人1之间分配一个剩余；如果参与人1选择“据为己有”（即图3中的OUT），则外部选择权结果为（x1，x2），x1为参与人1的收益，x2为参与人2的收益；如果参与人强烈地关注收益的平等性，则导致平等结果的设计可能更能体现他们的考虑。基于这样的逻辑，如果外部选择权不平等，则参与人2可能不考虑参与人1放弃的可能收益，不平等的选择权可能导致了参与人2仅为自己的利益考虑。相对平等的外部收益似乎可以使得参与人2在决策时更加关注参与人1放弃的外部收益。

Servátka和Vadovi 利用被试间设计和策略方法在新西兰坎特伯雷大学分别实施了含有26组被试的不平等外部选择权设置和平等外部选择权设置的实验。不平等的外部选择权设置中，参与人1首先得到10单位代币；如果选择IN，则接下来由参与人2在两人之间分配20单位代币，参与人1获得y单位代币，而参与人2获得20-y单位代币；如果参与人1选择OUT，则参与人1获得10单位代币，而参与人2的收益为0。平等外部选择权设置唯一与不平等外部选择权设置不同的是，当参与人1选择OUT时，参与人1和参与人2均获得5单位货币。在两种设置中，为了避免可能的混合效应他们保持了外部收益之和不变，即x1+ x2=10。

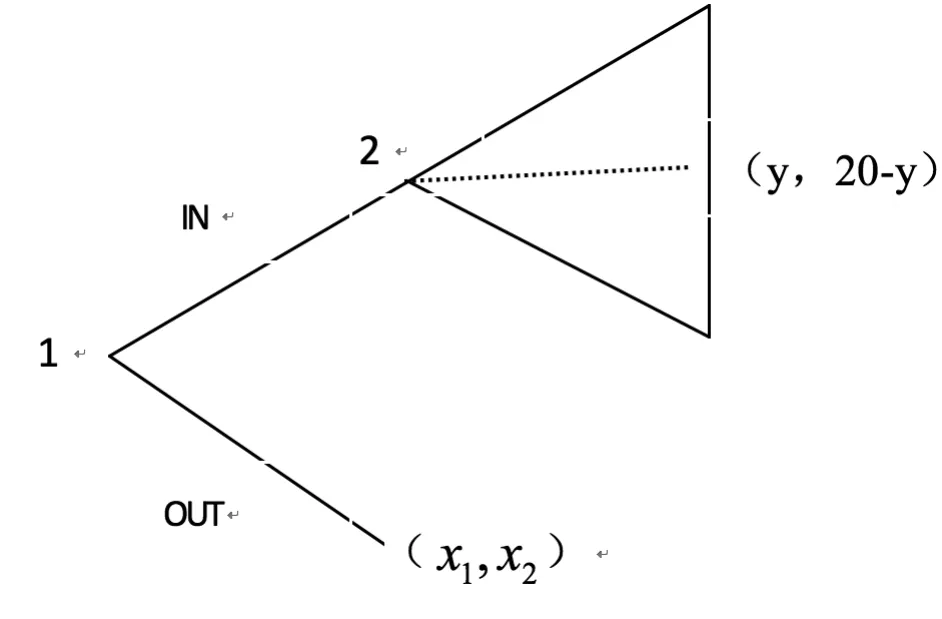
图3　Servátka和Vadovi 的实验结构

然而实验结果⑨参与人1的行为与DG的实验结果一致，随着x1的增大，选择归还失主的比例越来越少，不平等外部选择权设置中27%（7/26）的被试选择了归还，而平等外部选择权设置中，77%（20/26）的被试选择了归还。并没有为BGS的对参与人2的猜想提供证据，在不平等外部选择权中，参与人2选择的y值均值为6.12，平等外部选择权设置中参与人2选择的y值均值为5.19，检验结果也表明参与人2的行为在两种设置下并不存在显著区别，因此他们得出结论：外部选择权的不平等并不影响丢包博弈中参与人2的行为，丢包博弈之谜仍然未能得到解释。

四、外部选择权的凸显性与丢包博弈之谜

根据Batigalli和 Dufwenberg（2009）的心理前向归纳理论（psychological forward induction），参与人1放弃的外部选择权反映了他有更高的希望从而期待对方返还一个更高的y，如果参与人2是内疚规避的（guilt-aversion），他对参与人1更新的信念会表现慷慨，外部选择权越高，参与人1的更新信念也就越高，从而导致内疚规避的参与人2分配更多的金钱给参与人1。

Cox等（2010）试图解释DG提出的丢包博弈之谜：参与人1放弃的外部选择权大小不影响参与人2的行为。他们质疑了DG报告的参与人2选择的y与参与人1放弃的x的不相关性，认为y对x的反应取决于参与人2感知到的外部选择权大小的凸显性，参与人2决策时必须意识到参与人1放弃的x的大小从而对x做出反应。Cox等认为DG设计的原始协议可能使得放弃的外部选择权对参与人2并不凸显，因此他们改变了DG实验设计中的两个协议：第一，改变了目前所有丢包博弈实验中对参与人2使用的策略方法，而采用了直接反应的方法（即序贯执行）；第二，通过纸币凭证代替DG实验中采用的书写数字代表决策的方法。

策略方法是Selten（1967年）提出的用于诱导决策的方法。关于策略方法是否影响回应者的行为，Brandts 和Charness给了一个综述，但他们并没有给出一个统一的结论，回答这个问题似乎要回到具体的情境中。在一个与丢包博弈实验类似的信任博弈实验中，Casari 和Cason（2009）利用一个简单的信任博弈结构⑩Casari 和Cason（2009）与本文第一部分介绍的Berg（1995）的信任博弈实验略有不同，Casari 和Cason（2009）中的参与人A选择的Ma被限定为只有两个值0或者10，如果Ma= 10则参与人B得到5Ma即50，而Berg（1995）中参与人B得到3Ma。直接反应方法是参与人B知道参与人A的选择之后再做出决策，而策略方法是参与人B不知道参与人A决策的情况下直接做出决策，而仅当Ma= 10参与人B的决策才实施。，测度了策略方法和直接反应方法对博弈参与人行为的影响，结果表明策略方法对信任者的行为没有显著影响，而策略方法显著地降低了被信任者的可信水平；直接反应方法下被信任者平均给予信任者12.6点，而策略方法下被信任者平均返还值为7.4点。对于真实货币或者纸币凭证与书写数字代替决策是否产生不同的效应，目前没有文献研究此类问题。

Cox等人利用直接反应方法和被试间设计在新西兰坎特伯雷大学总共执行了两设置（x=4和x=7）的112组被试的丢包博弈实验。参与人1首先得到一个统一规格的含有4（或者7）张单位纸币凭证的信封，如果参与人1将信封“据为己有”，则参与人2得到一个更大的含有空白纸条的牛皮信封，且无需做出决策；如果参与人1选择“归还”，则与其配对的参与人2得到的大牛皮信封中含有：4（或7）张单位纸币凭证的统一规格信封，其上标有“他人的凭证”，和一个标有“我的凭证”的统一规格空信封，以及另外的16（或者13）张单位纸币凭证。参与人2决定将总共20张单位纸币凭证分别放到标有“我的凭证”和“他人的凭证”的信封中，分别代表参与人2和参与人1的收益。

Cox等人的实验结果表明，参与人1的行为与DG实验结果无显著区别，即使改变外部选择权对参与人2的凸显性以后，参与人2的行为在不同的外部选择权设置下仍然没有显著区别，x=4设置中参与人2给参与人1的信封中平均含有6.61新币，而x=7设置中参与人2给参与人1的信封中平均含有6.00新币。他们推测，之所以信任博弈中存在丢包博弈实验中不存在的互惠现象，是因为信任博弈中信任者的投资行为改变了被信任者的可选行为集，而丢包博弈实验中参与人2只能分配总价值一定的“包”。外部选择权的凸显性仍然没能成为打开丢包博弈之谜的钥匙，正互惠理论无法对丢包博弈做出合理的预测。

五、结 语

Dufwenberg 和Gneezy在 2000年提出的丢包博弈中丢包人的决策行为与捡包人放弃的外部选择权的大小不存在相关关系，这对近几十年发展起来的互惠理论提出了挑战。本文首先回顾了最后通牒博弈、信任博弈、偷袭者博弈和礼物交换博弈等博弈模型中存在的互惠现象，进而回顾了Dufwenberg 和Gneezy 2000年提出的丢包博弈之谜以及其他学者给出的丢包博弈实验的证据，然后继续追踪了学者的后续研究：Servátka和Vadovi （2009）验证了Brandts等（2006）的猜想，可能是不平等的外部选择权导致了丢包人的决策行为与捡包人放弃的外部选择权的不对称性，实验结果表明平等的外部选择权并没有改变这一关系。Cox等（2010）尝试用外部选择权对参与人2的凸显性来破解丢包博弈之谜，在实施了直接反应和用纸币凭证代替书写决策数字之后，仍然没有改变丢包人的决策行为与捡包人放弃的外部选择权之间的不对称性，丢包博弈之谜仍旧是个悬而未决的谜。

互惠理论对于研究我国当前经济新常态下企业行为和市场绩效有重要的意义，目前为止，学界对互惠的条件和边界仍没有统一的定论。破解丢包博弈之谜，对探究当前我国市场经济条件下企业的竞争与合作、多成员之间的团队创新有重要的启示意义。

［参考文献］

［1］ 李晓义，李建标. 互惠、信任与治理效率——基于比较制度实验的研究［J］. 南开经济研究，2009（1）：101-121.

［2］ 韦倩. 强互惠理论研究评述［J］. 经济学动态，2010（5）：106-111.

［3］ 李建标，庞荣辉. 公平偏好的产权效应——以最后通牒博弈实验为例. 2010， 工作论文.

［4］ 夏纪军. 中国的信任结构及其决定——基于一组实验的分析［J］. 财经研究，2005（6）： 39-51.

［5］ 陈叶烽. 亲社会性行为及其社会偏好的分解［J］. 经济研究，2009（12）： 131-144.

［6］ Rabin， M. Incorporating fairness into game theory and economics ［J］. American Economic Review， 1993， 83（5）： 1281-1302.

［7］ Fehr， E.， Schmidt， K. M. A theory of fairness， competition and cooperation ［J］. Quarterly Journal of Economics， 1999，114（3）：817-868.

［8］ Bolton， G. E.， Ockenfels， A. ERC： a theory of equity， reciprocity， and competition ［J］. American Economic Review， 2000， 90（1）：166-193.

［9］ Charness， G.， Rabin， M. Understanding social preferences with simple tests ［J］. Quarterly Journal of Economics， 2002， 117（3）：817-869.

［10］ Guth， W.， Schmittberger， R.， Schwarze， B. An experimental analysis of ultimatium bargaining ［J］. Journal of Economic Behavior and Organization， 1982， 3（4）： 367—388.

［11］ Cameron， L. Raising the stakes in the ultimatum game： experimental evidence from Indonesia， Discussion Paper， 1995， Department of Economics， Princeton University.

［12］ Hoffman， E.， McCabe， K. Smith， V. On expectations and monetary stakes in ultimatum games ［J］. International Journal of Game Theory， 1996， 25（3）： 289-301.

［13］ Henrich， J.， Boyd， R.， Bowles， S. et al. In search of homo economicus： behavioral experiments in 15 small-scale societies. American Economic Review， 2001， 91（2）：73-78.

［14］ Berg， J.， Dickhaut. J.， McCabe K. Trust， reciprocity， and social history ［J］. Games and Economic Behavior ， 1995， 10（1）： 122-142.

［15］ Cox J C. How to identify trust and reciprocity ［J］. Games and Economics behavior， 2004， 46（2）： 260-281.

［16］ Abbink， K.； Irlenbusch， B.； Renner， E. The moonlighting game ［J］. Journal Economics Behaviror and Organization， 2000， 42（2）：265-277.

［17］ Falk， A.； Fehr， E.， Fischbacher， U. Testing theories of fairness—Intentions matter ［J］. Game and Economics and Behavior， 2008，62（1）：287-304.

［18］ Engelmann， D.， Strobel， M. Inequality aversion and reciprocity in moonlighting games［J］. Games， 2010， 1（4）：459-477.

［19］ Akerlof， G. A. Labor contracts as partial gift exchange ［J］. The Quarterly Journal of Economics， 1982， 97（4）：543-569.

［20］ Akerlof， G.， Yellen， J. Fairness and unemployment ［J］. American Economic Review 1988，78（2）：44-49.

［21］ Akerlof， G.， Yellen， J. The fair-wage effort hypothesis and unemployment ［J］. Quarterly Journal of Economics， 1990， 105（2）：255-283.

［22］ Fehr， E.， Kirchsteiger， G.， Riedl， A. Does fairness prevent market clearing？ An experimental investigation ［J］. Quarterly Journal of Economics， 1993， 108（2）：437-459.

［23］ Fehr， E.， Gachter， S. Kirchsteiger， G. Reciprocity as a Contract Enforcement Device： Experimental Evidence［J］. Econometrica， 1997，65（4）：833-860.

［24］ Dufwenberg，M.， Gneezy， U. Measuring beliefs in an experimental lost wallet game ［J］. Games and Economic Behavior， 2000， 30（2）：163-182.

［25］ Brandts，J.， Güth， W.， Stiehler， A. I Want YOU！ An experiment studying motivational effects when assigning distributive power ［J］，Labour Economics ，2006，13（1）： 1-17.

［26］ Charness， G.， Haruvy， E.， Sonsino， D. Social distance and reciprocity： an internet experiment［J］. Journal of Economics Behavior and Organization， 2007， 63（1）： 88-103.

［27］ Maroš Servátka Radovan Vadovi ， Unequal outside options in the lost wallet game ［J］. Economics Bulletin， 2009， 29（4）： 2870-2883. ［28］ Battigalli， P.， Dufwenberg， M. Dynamic psychological games ［J］. Journal of Economic Theory， 2009， 144（1）： 1-35.

［29］ Cox， J.， Servátka， M.， Vadovi ， R. Saliency of outside options in the lost wallet game ［J］. Experimental Economics， 2010， 13（1）：66-74.

［30］ Selten， R. Die Strategiemethode zur Erforschung des eingeschränkt rationalen Verhaltens im Rahmen eines Oligopolexperiments， in H. Sauermann （ed.）， Beiträge zur experimentellen Wirtschaftsforschung， Tübingen： Mohr， 1967，136-168.

［31］ Brandts， J.， Charness， G. the strategy verse the direct-response method： a survey of experimental comparisons， Working papers，2010. ［32］ Casari. M.， Cason， T. The strategy method lowers measured trustworthy behavior ［J］. Economics Letters， 103（3）： 157-159.

〔执行编辑：周冬〕

The Puzzle of Lost Wallet Game： the Challenge of Theory of Reciprocity

Zhao Yu-liang
（Nankai University， Binhai， 300270， China）

Abstract：The theory of reciprocity is one of main topics of behavioral economics and experimental economics in recent several decades. However， lost wallet game proposed by Dufwenberg and Gneezy in 2000 indicated that the reward behavior of wallet owner and the size of the outside option the wallet picker forgone are uncorrelated or weakly correlated. Servátka and Vadovič （2009） and Cox et al （2010） were trying to use the inequality of outside option and the saliency of outside option to the wallet loser to shed some light on the puzzle of lost wallet game， but their experiments hasn’t solved the asymmetry between the wallet loser’s reward behavior y and the outside option the wallet picker forgone. Therefore，the lost wallet game is still an open puzzle.

Key Words：puzzle of lost wallet game； reciprocity theory； inequality of outside option； saliency of outside option

［中图分类号］F062.6

［文献标识码］A

［文章编号］2095-7572（2016）03-0106-11

［收稿日期］2016-4-2

［作者简介］赵玉亮，南开大学滨海学院讲师，管理学博士，研究方向：制度、产业行为和实验经济学，1982年，山东宁津人。