Kinetic effects of nanosecond discharge on ignition delay time☆

Xingqian Mao,Guoxiu Li,Qi Chen*,Yujun Zhao

School of Mechanical,Electronic and Control Engineering,Beijing Jiaotong University,Beijing 100044,China

1.Introduction

In recent years,non-equilibrium plasma assisted combustion has provided new opportunities for combustion research,because it can shorten the ignition delay time,improve the stability of the flame,extend the lean blowout limit and can be used to control emissions[1–4].Plasma produces large amounts of active species,which modify the thermal,kinetic and transport effects in combustion[5].Different types of nonequilibrium plasma,including microwave discharge[1,6],direct current discharge[2],dielectric barrierdischarge[7,8],radio-frequency discharge[9],Corona discharge[10,11]and so on,have been implemented to study plasma assisted combustion and ignition.

As the discharge duration of nanosecond discharge is on the order of nanosecond,the complex interaction mechanism between plasma kinetics and flame chemical kinetics can be separated to study[12].In addition,high values of local electric field to number density ratioE/N,in the range of 100–1000 Td(1 Td=10-17V⋅cm2),allows for efficient of radicals and excited species via electron impact reactions,which kinetically enhances the ignition and flame stabilization processes[13].So,among different types of plasmas,many researchers are interested in the role of nanosecond discharge on ignition, flame speed and flame stabilization through experimental and numerical study[3,4,7,12–21]in the past decade.

N.L.Aleksandrovet al.[14–15]measured the ignition delay time of methane-containing mixtures under the action of a high-voltage nanosecond discharge by the shock tube experiment,and the ignition dynamics was further simulated numerically with allowance for experimental data on the dynamics of the discharge current and discharge electric field.Sharath Nagarajaet al.[16]used an optimized chemical kinetics mechanism to investigate the effect of non-equilibrium plasma on two-stage ignition ofn-heptane.All of their studies showed that the application of nanosecond discharge could result in a reduction of ignition delay time observably.Wenting Sunet al.[17]showed that non-equilibrium plasma could dramatically accelerate the CH4oxidation at low temperature mainly due to the production of O which was initiated by electron dissociation reactions in the plasma.Furthermore,Sharath Nagaraja et al.[13]showed that plasma action could result in a significant increase in O and H density of the lean premixed H2/O2/N2flame,and the electron impact dissociation and excitation process had a major impact on the temperature and species while the Joule heating alone did not account for the observed effects of the plasma.

In most literature researches[14,15,17,19],the gas mixture discharge is generated in inert diluent gases,such as argon and helium.It is more practical to study methane–air ignition at atmospheric pressure.The objective of this study is to use a modified chemical kinetics mechanism to simulate non-equilibriumplasma assisted ignition and furthermore carry out the chemical kinetics on ignition delay times of methane–air mixture under nanosecond discharge by zero-dimension numerical simulation.

2.Kinetic Model and Simulation Methods

Timescale of the discharge process is on the order of nanosecond,whereas the ignition process develops on microsecond timescale.Kinetic mechanisms of the two processes are quite different,and need to be separated in two parts to study.

Plasma discharges can produce a wide range of stable and metastable species which are potential to enhance ignition,especially in the case of pre-mixture combustion.However,it's quite difficult to decide which species and reaction pathways are most important for ignition enhancement,and furthermore to build a practical kinetic model.In fact,only a few species are critical to the ignition enhancement.Careful selection of them will help to simplify the kinetic model and accurately predict the plasma assisted ignition[22].

In our work,the methane–air mixture produces a large number of atoms,radicals and electronically excited species under nanosecond discharge,which plays an important role in ignition.As the discharge process timescale is much smaller than that of ignition,the discharge duration can be neglected in ignition process.

2.1.Kinetic model

Nanosecond discharge simulation consists of two parts:production of the atoms and radicals in the nanosecond discharge process under high reduced electric field and particle decay in the subsequent afterglow process with zero reduced electric field.

The kinetic model for methane–air mixture ignition could be simplified during discharge process.In this work,we focus the dissociation impact of non-equilibrium plasma on CH4ignition delay time.The main components of air are O2and N2,thus the mixture can be simplified as CH4/O2/N2.The rotational state energy and the vibrational state energy of N2and O2molecules are significantly lower than the typical chemical reaction thresholds,which are insufficient to lead to the dissociation and excitation of other molecules.They are therefore neglected in this study.

The primary mechanism of gas excitation is the population of the electronic degrees of freedom by electron impact and the energy exchange among excited states at 100–500 Td[23].The excitation of Hertzberg metastable states （O2（c1），O2（C3Δu），O2（A））is substituted by an effective metastable statewith an excitation energy of4.5 eV[14].The electronically excited states ofN2play the vital role in the dissociation of O2and CH4molecules,and need to be considered in detail.The electronically excited N2（A3）,N2(B3Πg),N2（a′1）and N2(C3Πu)states with different excitation energy are separated to analysis when calculating the density of particles produced in the discharge process.The N2（A3，v=0-4）,N2（A3，v=5-9）and N2（A3，v=10-）states are substituted by an effective electronically excited state donated as N2(A)[24].The excitation rate constant is assumed to be equal to the sum of the excitation rate constants of the three states,and its quenching rate constant is taken equal to that of the N2（A3）state.This approximation is based on the assumption of fast collisional energy exchange between these states.The excitation of one effective state donated as N2(B)is substituted for the excitation of N2(B3Πg),N2（B′3）and N2(W3Δu)triplet states.The excitation rate constant is assumed to be equal to the sum of the excitation of the three triplet states,whereas its quenching rate constant is equal to that of the N2(B3Πg)state[14].The excitation of N2(a1Πg),N2（a′1）and N2(w1Δu)singlet states is also substituted by an effective state donated as N2(a′).The excitation rate constant is assumed to be equal to the sum of the excitation of the three singlet states,whereas the quenching rate is equal to that of the N2（a′1）state[14].In addition,the excitation of an effective state donated as N2(C)is substituted for the excitation of N2(C3Πu),N2(E3)and N2(a″1)states[24].The excitation rate constant is assumed to be equal to the sum of the excitation of the three states,and the quenching rate is equal to that of the N2(C3Πu)state.

The density of negative ions is much lower than that of the electrons when the temperature of the mixture is over 1000 K,and they are not considered in our simulation[15].Meanwhile,the complex particles,such as O3,,and,are neglected due to the low dissociation energy and their rapid decay under high temperature conditions[14].The positive ions including,N+,O+,,,andare involved in the plasma kinetic model.Collisions between electron and any intermediate species generated in plasma are neglected because of their low concentration.

Kinetic model of CH4/O2/N2mixture during the discharge is shown in Table 1.Electron-impact dissociation reactions,electron-impact excitation reactions,electron-impact ionization reactions,quenching of the electronically excited states reactions,charge exchange reactions,electron ion recombination reactions,attachment reactions,and dissociation and recombination of nitrogen–oxygen molecules are involved in this modified model.Electron transport coefficients and rate constants of electron-impact reactions(R1–R14)under a given value ofE/Nare calculated from collision-section data by solving the classical two term approximation Boltzmann equation.The cross-section data are obtained from the LXCAT online database.The GRI-mech3.0 is applied to the ignition process which contains of 53 species and 325 elementary reactions[34].

2.2.Simulation methods

The kinetic model of CH4/O2/N2mixture in the discharge process is calculated by zero-dimensional plasma kinetics solver ZDPlasKin which is a FORTRAN module[35].The electron transport and rate coefficients are provided by the Boltzmann equation solver BOLSIG+[36]incorporated in ZDPlasKin.The time evolution of the species densities in non-equilibrium plasma is solved by the Eq.(1)

where i is the types of the species produced in the plasma,Niis the number density of speciesi,i=1…imax,Qijis the source rates of species corresponding to the contributions from different reactions,and j=1…jmax.imaxand jmaxare the total number of species and reactions included in the plasma kinetic model respectively.

The path flux of the species is analyzed by Pumpkin which is a tool to find all principal pathways in plasma chemical models[37].The flux of molecules or atoms produced(the negative number represents consumed)by a certain reaction for a given time interval is solved by the Eq.(2)

where miris the positive(or negative)number of particles ofiproduced(or consumed)by the pathwayPr,fris the rate of pathwayPr,sijrepresents the number of particles of species i produced by reaction j,andxjris the multiplicity of reactionjin the pathwayPr(zero ifjdoes not occurinPr).Here,ris the number ofpathways considered per branching point treatment.

In this work,the plasma ignition delay time of the mixture is calculated with anE/Nof 250 Td at atmospheric pressure(P=0.1 MPa)and an initial temperature ofT0=1300 K.The equivalence ratio ϕ of methane–air is 1.0 and the discharge duration is 16.5 ns.The system is assumed to be adiabatic in the simulation.The reduced electric fieldE/Nis a decisive parameter for discharge process because it has a great impact on energy release and the electron energy distribution[20].In order to simplify the model,the square wave of a fixed value ofE/Nis applied in this study.The ignition processis calculated by using the conditions output by ZDPl as K in.The ignition delay can be calculated by solving the energy equation.

Table 1Kinetic model of CH4/O2/N2 mixture during nanosecond discharge.(the gas temperature T and the electron temperature T e are in K,σ is the collision cross section,R is the ratio coefficient of different neutral species M)

Table 1(continued)

3.Results and Discussion

3.1.Temporal evolution of particles in plasma model

The dissociation effect of plasma leads to the production of atoms and radicals,such as electrons and electronically excited nitrogen,so this process needs to be analyzed particularly.Electron-impact reactions R1-R14 dominate the production of particles in nanosecond discharge process.A large number of CH3,CH2,H,O,N radicals are produced by electron impact dissociation reactions R1–R4.The mole fractions of electronically excited O2and N2increase sharply due to electron-impact excitation reactions R5–R9.At the same time,the mole fractions of electrons and positive ions also show a growth tendency through electron-impact ionization reactions R10–R14,as shown in Fig.1(a)–(c).All particles present an exponential growth trend in this process.

In the afterglow period,the main pathways of the production of CH3,CH2,O,and H radicals are the quenching of the electronically excited N2states with O2,CH4molecules reactions,as well as the recombination reactions between electrons and positive ions,such as CH4+,CH3+,and O2+.Fig.1(a)shows that the mole fractions of CH3,CH2,O,and H radicals increase slightly first and then tend to be stable in the afterglow part.The mole fractions of electronically excited species and positive ions decrease in the discharge afterglow because of decay,as is shown in Fig.1(b)–(c).Thus,the rates of the concerned elementary reactions decrease with time evolution.Without electric field,electrons are attracted to move to positive ions and recombine with them and the evolution of electrons also presents a decrease trend.

3.2.Path fl ux analysis of O and H in plasma model

N.L.Aleksandrovet al.[15]researched on the ignition mechanism of the CH4/O2/Ar mixture under the effect of non-equilibrium plasma and found that the production of CH3at the beginning of ignition is not important,because the efficiency of CH3in the ignition processes is much less than that of O and H.At the meantime,the mole fraction of CH2is relatively lower than that of O and H.The production mechanism of O and H radicals during the discharge and afterglow process is therefore a cleat,which is helpful to understand their effects on ignition.

In this paper,the mechanisms of O-abstraction and H-abstraction reactions in the nanosecond discharge and afterglow process are studied respectively.During the nanosecond discharge process,a great many electrons are produced by the ionization reactions between electrons and neutral molecules,while the electronically excited N2states are produced by collisions between electrons and N2.The electron-impact dissociation reaction of O2(R2)and the excited N2states dissociation impact on O2dominate the production of O.Results in our study indicate that the largest percentage of O,49%,comes from R2 and the contribution by quenching reactions of N2(B)(R23)and N2(C)(R31)is 32%and 16%respectively.Though the mole fractions of N2(A)and N2(a′)have a quite large proportion as is depicted in Fig.1(b),it is observed in Fig.2 that the quenching reaction rates of N2(A)(R16)and N2(a′)(R27)are lower than those of N2(B)(R23)and N2(C)(R31),and they have little effect on the dissociation of O2.When comes to the afterglow process,O2+is consumed by the recombination reaction with electron(R57)which contributes to a few part of O in the afterglow.More than 90%of O are produced from the quenching reactions of the four electronically excited N2states in this process.At the beginning,the mole fraction of the excited N2states remains peak and the reaction rates with O2still keep at a high level.The mole fraction of O continues to grow in a short time as is shown in the afterglow part in Fig.1(a),and it remains stable gradually with the decay of the excited N2states and the decrease of the quenching reaction rates.

Fig.1.Temporal evolution of the mole fraction of(a)atoms and radicals(b)electronically excited molecules(c)electron and positive ions produced in nanosecond discharge and afterglow process in a stoichiometric methane–air mixture.T0=1300 K,P=0.1 MPa,E/N=250 Td,the discharge duration is 16.5 ns.

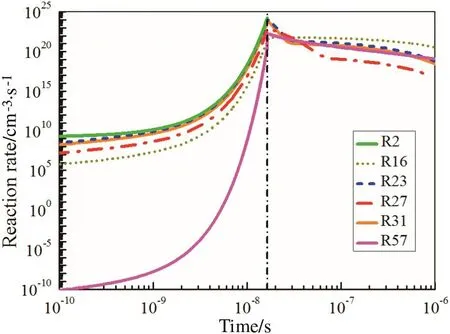
Fig.2.Rates of the O-abstraction reactions in discharge and afterglow.E/N=250 Td.

Similarly,among the H-abstraction reactions,the rates of electron impact reactions with CH4in the nanosecond discharge R3 and R4 are higher than others,as is shown in Fig.3.About 80%of the H is produced by the two reactions.The effect of the electronically excited N2states on H-abstraction is small in this process.The excitation energy of N2(A)is comparatively low and its effect on the dissociation of CH4is small.The quenching reactions of N2(a′)(R36)and N2(C)(R37)account for 5.6%and 7.8%of H produced in the 16.5 ns discharge duration respectively.The reaction rate of quenching of N2(B)(R35)is slower than that of N2(a′)(R36)and N2(C)(R37),as is shown in Fig.3 and it contributes to the production of H slightly.The charge exchange reaction between N2+and CH4also contributes to 4.3%of the production of H.In the afterglow stage,the quenching reactions of the electronically N2states dominate the dissociation of CH4.The production of H coming from the quenching reactions of N2(B),N2(a′)and N2(C),accounts for the total H produced during the afterglow 1.3%,51.7%and 22.4%respectively.7%of H is produced by R47.Among the recombination reactions(R61–R63)between electrons and CH4+,CH3+,R63 is the main pathway,accounting for 13.6%.

Fig.3.Rates of the H-abstraction reactions in discharge and afterglow.E/N=250 Td.

The total path flux analyses of the production of O and H are carried out to investigate the important pathways of the two radicals' production during the whole discharge process.The percentage contribution of each path is given in Fig.4.In summary,the most effective production reactions of O are quenching reactions of the electronically excited N2states all over the discharge,and electron impact dissociation reactions rank second.Among the H-abstraction reactions,the contribution from both electrons and electronically excited N2states are considerable.

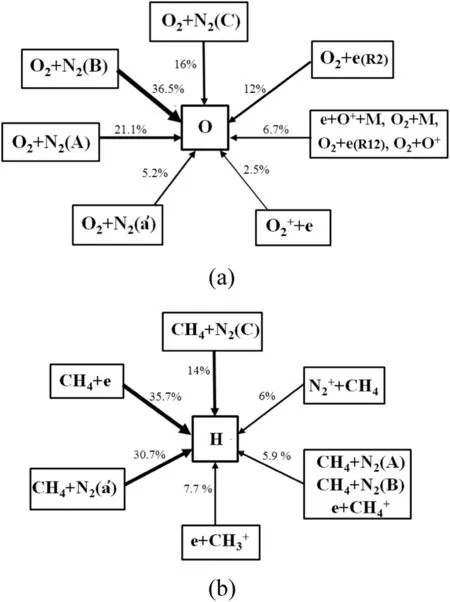
Fig.4.Path flux of the production of(a)O and(b)H in discharge and afterglow.E/N=250 Td.

3.3.Ignition delay time in different discharge conditions

There are many ways to define the ignition delay time in literatures.The calculated ignition delay time in this paper is defined as the time interval between the starting point of calculation and the instant of maximum rate of temperature rise(max d T/d t).

The autoignition delay time of the stoichiometric methane–air mixture calculated with an initial temperature of 1300 K and at atmospheric pressure is 11.64 ms.However,the ignition delay time with plasma in the same initial conditions is 0.715 ms,which indicates that nanosecond discharge has a dramatically promotion on the reduction of ignition delay with respect to autoignition.The value ofE/Ncontrols the direction of the energy deposition and the composition of the active particles produced in the discharge[23],and needs to be analyzed in particular.

3.3.1.Analysis of the energy deposited during the discharge

The discharge deposited power density P′is calculated by Eq.(3)[23]

where j′is the current density,e is the value of electron charge,Neis the electron density,vdris the electron drift velocity,and μe(E/N)is the electron mobility in a given reduced electric field.

The discharge deposited energyWis calculated by Eq.(4)

where tdis the discharge duration.

Fig.5 shows the evolution of deposited power density during the nanosecond discharge at the initial condition.At the beginning of the discharge,the value of deposited power density changes slightly because of the slow accumulation of electrons.The power density has the same exponential growth trend as electrons with time evolution and its value peaks at the end of the discharge.The calculated deposited energy in the 16.5 ns discharge duration at 250 Td is 28.47 mJ·cm-3.

Fig.5.Temporal evolution of deposited power density during the nanosecond discharge.E/N=250 Td.

The value of deposited energy is determined by two parameters,E/Nandtd,which are deduced from Eqs.(3)–(4).Thus,the ignition delay times of a methane–air mixture are calculated under different discharge duration and reduced electric field in order to find out the effect of the two parameters on ignition delay.

3.3.2.Effect of discharge duration on ignition

The accumulation of deposited energy is tiny before 15 ns,and its effect on shortening the ignition delay is relatively unapparent,so the ignition delay times are calculated with discharge durations of 15 ns,15.3 ns,15.6 ns,15.9 ns,16.2 ns and 16.5 ns at 250 Td respectively.

Fig.6 shows that the ignition delay time reduces with the increase of discharge duration.Longer discharge duration results in more deposited energy being available to excited nitrogen species and more electrons,and it promotes the production of O and H,as is observed in Fig.7(a)–(b).Even if when the discharge duration is 15 ns with 1.21 mJ·cm-3deposited energy,the ignition delay time still shortens 3 ms,illustrating the significantly promotion of the non-equilibrium plasma on ignition.

It is noted that the increase of O and H is proportional to the discharge duration.This may be due to the exponential growth of the deposited energy which also increases in proportion during the same discharge duration interval.

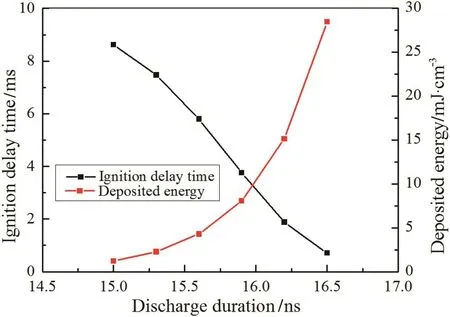
Fig.6.Ignition delay time and corresponding deposited energy with different discharge durations.E/N=250 Td.

3.3.3.Effect of reduced electric field strength on ignition

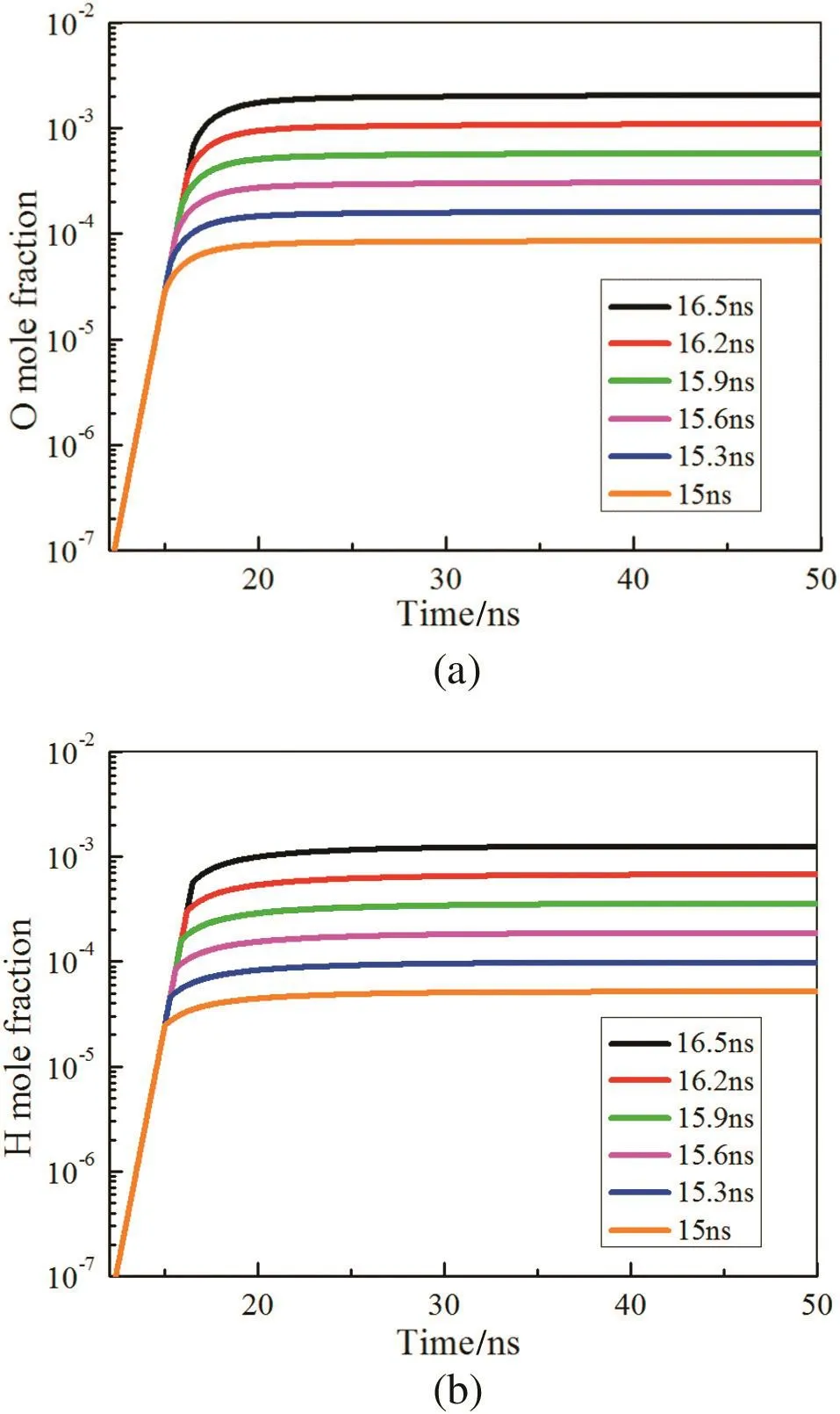
Fig.7.Temporal evolution of(a)O and(b)H with different discharge durations.E/N=250 Td.

The effect of reduced electric field strength is similar to that of the discharge duration,which controls the energy deposition during discharge.However,the production of electrons is sensitive to the strength of E/N,and a small value change of E/N will cause dramatically change of deposited energy.In this part,the ignition delay times are calculated at 240 Td,242 Td,244 Td,246 Td,248 Td and 250 Td with fixed discharge duration of 16.5 ns respectively.

Fig.8 shows that the ignition delay time declines with the growing strength ofE/N.More deposited energy is accumulated with largerE/N,which leads to more production of O and H,as is depicted in Fig.9(a)–(b).A notable phenomenon different from the effect of discharge duration is that the larger strength of E/N has an earlier increase time point of the mole fraction of radicals,because the system can accumulate the same energy with a shorter time interval at a largerE/N.

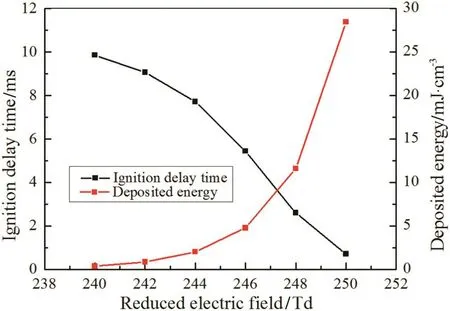
Fig.8.Ignition delay time and corresponding deposited energy with different strength of E/N.t d=16.5 ns.

The discussion above has shown that nanosecond discharge has a markedly accelerating effect on ignition,even if when the mole fractions of the active radicals and species are small.The nanosecond discharge process provides a small amount of seed radicals to initiate this“self-accelerating”process which acts as a catalyst,and the quantity of radicals introduced initially is not a critical factor[16].This suggests that the addition of radicals has a strong impact on the initiation time of the ignition and a small mole fraction can change the chemical kinetics during the ignition process and shorten the timescale of ignition delay times.

3.4.Chemical kinetic analysis on plasma assisted ignition

3.4.1.Temporal evolution of temperature and radicals

Fig.10 shows the temporal evolution of temperature for cases without and with plasma under different discharge duration.The temperature of the mixture changes faster with longer discharge duration.A rapid temperature rise is observed at the initial timing which decreases with the shortened discharge duration,and this phenomenon disappears in the autoignition process.To clarify the ignition delay time and the tiny temperature rise dependence on nanosecond discharge,the temporal evolution of intermediate radicals produced during autoignition and plasma assisted ignition is analyzed,as is shown in Fig.11(a)–(b).The condition with 16.5 ns discharge duration at 250 Td is selected by reason of its biggest temperature rise.

The reaction path CH4→CH3→CH2O→HCO→CO→CO2is well known in the kinetics of the autoignition of CH4[38].Fig.11(a)shows that the mole fraction of intermediate species such as HO2and CH2O increases slowly during the autoignition.However,the nanosecond discharge supplies the active radicals like CH3,CH2,H,O,etc.which accelerate the oxidation of CH4.The timing of the maximum rate of temperature rise is analyzed at the initiative time of plasma assisted ignition,and we find that reactions:O+CH4=OH+CH3and H+CH4=CH3+H2promote the production of CH3,OH and H2with the input Hand Oradicals.Then H2,H,CH2O and CO are produced by reactions O+CH3=H+CH2O and O+CH3=H+H2+CO.Meanwhile,CH2radical produced in the discharge also accelerates the rate of reactions CH2+O2=O+CH2O,CH2+O2=OH+H+CO and O+CH2=H+HCO.The discussions above illustrate that plasma has a significant impact on the production of intermediate radicals.The mole fraction of these radicals already has a relatively high value at initial time,which can change the chemical kinetics during the ignition.Consequently,the ignition delay time is dramatically shortened.

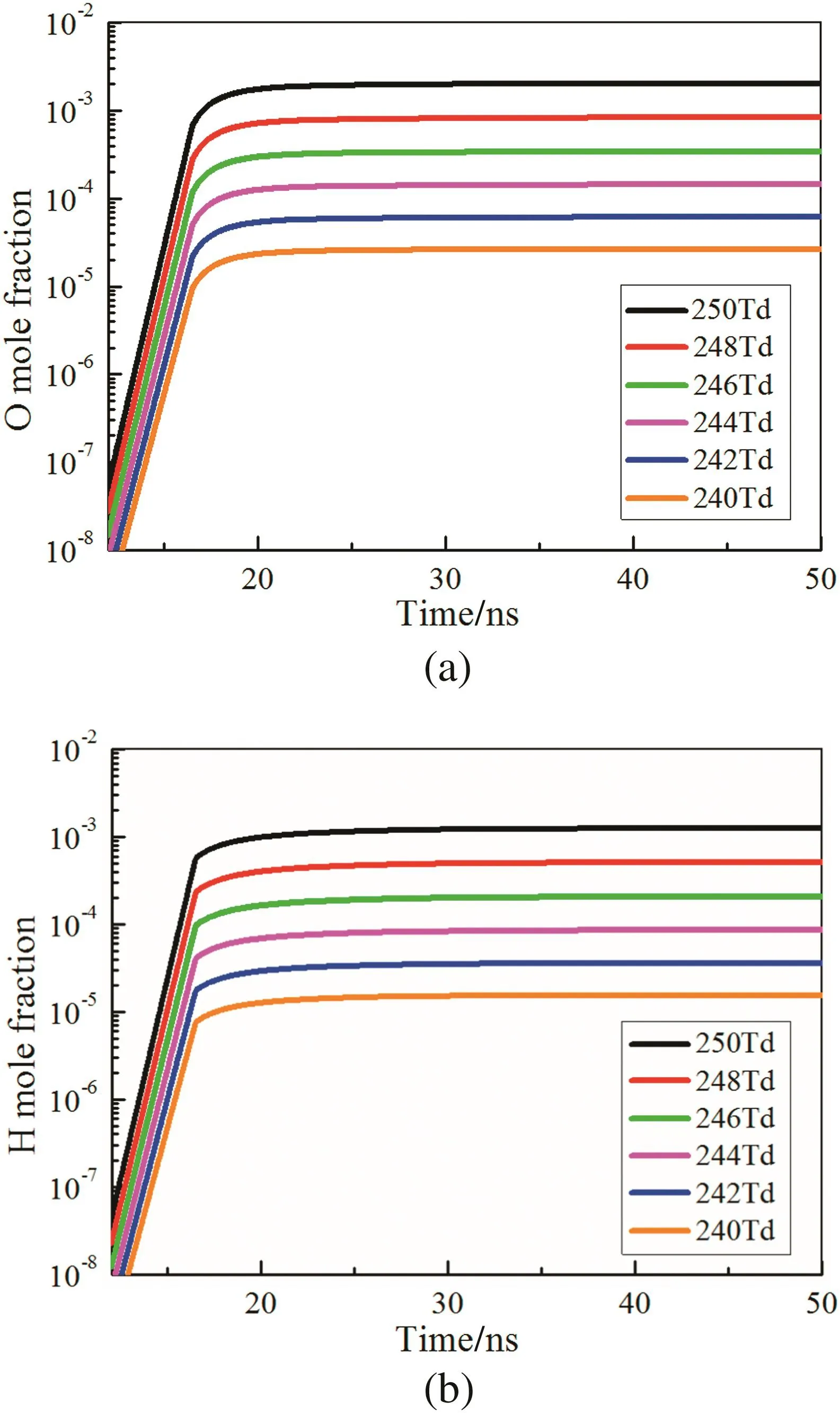
Fig.9.Temporal evolution of(a)O and(b)H with different strength of E/N.t d=16.5 ns.

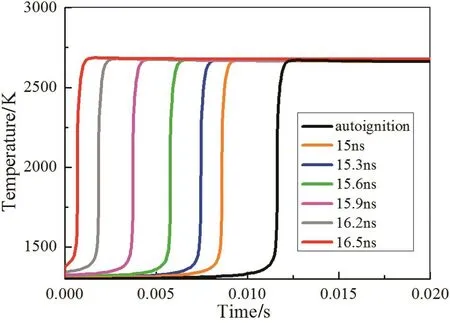
Fig.10.Temporal evolution of temperature for cases without plasma(autoignition),and for 15 ns,15.3 ns,15.6 ns,15.9 ns,16.2 ns and 16.5 ns discharge duration at 250 Td applied in the simulation.ϕ=1.0,T0=1300 K,P=0.1 MPa.

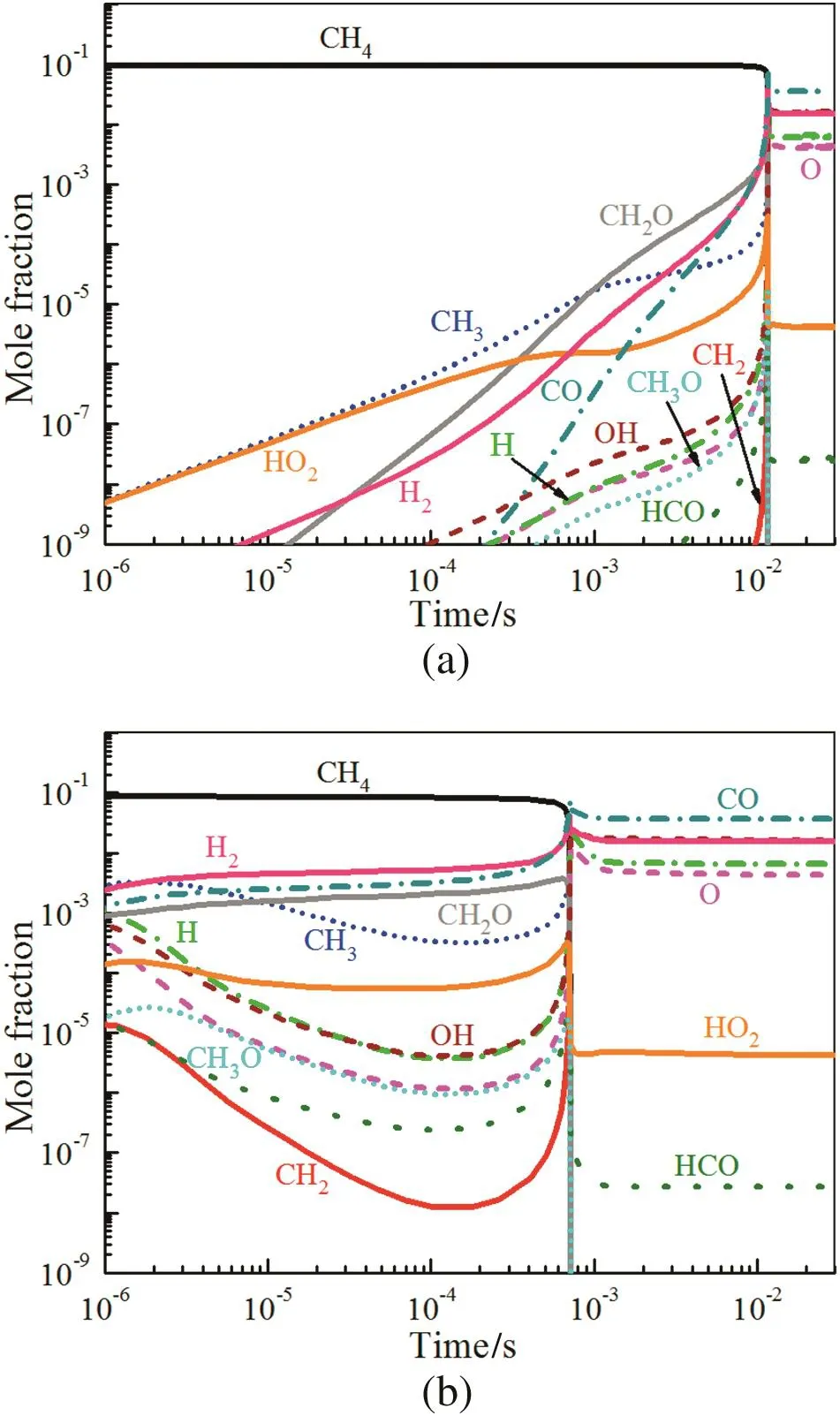
Fig.11.Mole fraction of intermediate radicals produced during(a)autoignition and(b)plasma assisted ignition at 250 Td with 16.5 ns discharge duration.ϕ=1.0,T0=1300 K,P=0.1 MPa.

3.4.2.Sensitivity analysis

Sensitivity analysis of ignition delay times for autoignition and plasma assisted ignition at0.1 MPa and initial temperature of 1300 K is conducted to gain further insight into the effect of nanosecond discharge on the ignition characteristics of the methane–air mixture.The discharge duration is 16.5 ns at 250 Td.The normalized sensitivity is defined as[39],

where τ is the ignition delay time of the methane–air mixture andkjis the rate constant of thej-th reaction.Negative value of sensitivity coefficient manifests the corresponding reaction has a promotion effect on ignition and vice versa.

The result of the sensitivity analysis is provided in Fig.12.It is noted that reactions CH3+O2=O+CH3Oand CH3+O2=OH+CH2O havethe high negative sensitivity coefficients,which indicate that the ignition chemistry is characterized by the two reactions during the autoignition process.Whereas,reaction H+O2=O+OH has the largest negative sensitivity coefficient to methane ignition with plasma because of the production of H radical during the nanosecond discharge,and plasma assisted ignition chemistry is characterized by this reaction.Reaction HO2+CH3=OH+CH3O also has a strong promotion impact,suggesting the importance of H and HO2on plasma assisted ignition.Reactions H+CH4=CH3+H2,OH+CH4=CH3+H2O and 2CH3+(M)=C2H6+(M)have high positive sensitivity coefficients on ignition and play an inhibition role in the reactivity both with and without non-equilibrium plasma.However,due to the atoms and radicals injected to the methane–air mixture,sensitivity coefficients of the inhibition reactions with plasma are much larger than that of autoignition.

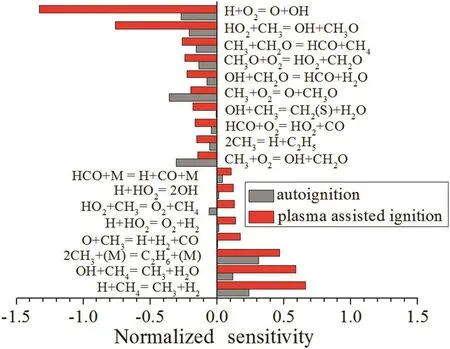
Fig.12.Sensitivity analysis for methane–air autoignition and plasma assisted ignition.

4.Conclusions

In this work,the chemical kinetics study of nanosecond discharge effects on ignition delay times of the methane–air mixture at atmospheric pressure by numerical simulation has been conducted.It was found that electronically excited N2states and electrons were important to the production of active radicals in the plasma model.The ignition delay times were calculated in different discharge conditions.The results showed that the strength of E/N and the discharge duration controlled the energy deposition and active particles production in the discharge,and the ignition delay time decreased with larger E/N and longer discharge duration.In the simulation,the ignition delay time was shortened and the chemical kinetics of ignition was changed by adding a small number of radicals,illustrating that the mole fraction of active radicals produced in a plasma was not a critical factor for ignition process.Furthermore,temperature and radicals analysis showed that a rapid temperature rise appeared at the initial timing of plasma assisted ignition and plasma promoted the production of intermediate radicals during the ignition process.Sensitivity analysis revealed that reactions involving H and HO2radicals were important to plasma assisted ignition.

[1]Z.Wang,J.Huang,Q.Wang,L.Hou,G.Zhang,Experimental study of microwave resonance plasma ignition of methane–air mixture in a constant volume cylinder,Combust.Flame 162(6)(2015)2561–2568.

[2]B.N.Ganguly,Hydrocarbon combustion enhancement by applied electric field and plasma kinetics,Plasma Phys.Control.Fusion 49(12B)(2007)B239–B246.

[3]G.Lou,A.Bao,M.Nishihara,S.Keshav,Y.G.Utkin,J.W.Rich,W.R.Lempert,I.V.Adamovich,Ignition of premixed hydrocarbon–air flows by repetitively pulsed,nanosecond pulse duration plasma,Proc.Combust.Inst.31(2)(2007)3327–3334.

[4]W.Kim,M.G.Mungal,M.A.Cappelli,The role of in situ reforming in plasma enhanced ultra lean premixed methane/air flames,Combust.Flame 157(2)(2010)374–383.

[5]Y.Ju,W.Sun,Plasma assisted combustion:Dynamics and chemistry,Prog.Energy Combust.(48)(2015)21–83.

[6]W.Tan,T.A.Grotjohn,Modelling the electromagnetic field and plasma discharge in a microwave plasma diamond deposition reactor,Diam.Relat.Mater.4(9)(1995)1145–1154.

[7]S.Nagaraja,V.Yang,Z.Yin,I.Adamovich,Ignition of hydrogen–air mixtures using pulsednanosecond dielectric barrier plasma discharges in plane-to-plane geometry,Combust.Flame 161(4)(2014)1026–1037.

[8]L.A.Rosocha,D.M.Coates,D.Platts,S.Stange,Plasma-enhanced combustion of propane using a silent discharge,Phys.Plasmas 11(5)(2004)2950–2956.

[9]N.Chintala,A.Bao,G.Lou,I.V.Adamovich,Measurements of combustion efficiency in nonequilibrium RF plasma-ignited flows,Combust.Flame 144(4)(2006)744–756.

[10]F.Wang,J.B.Liu,J.Sinibaldi,C.Brophy,A.Kuthi,C.Jiang,P.Ronney,M.A.Gundersen,Transient plasma ignition of quiescent and flowing air/fuel mixtures,IEEE Ttrans.Plasma Sci.33(2)(2005)844–849.

[11]J.Liu,F.Wang,G.Li,A.Kuthi,E.J.Gutmark,P.D.Ronney,M.A.Gundersen,Transient plasma ignition,IEEE Trans.Plasma Sci.33(2)(2005)326–327.

[12]W.Kim,J.Snyder,J.Cohen,Plasma assisted combustor dynamics control,Proc.Combust.Inst.35(3)(2015)3479–3486.

[13]S.Nagaraja,T.Li,J.A.Sutton,I.V.Adamovich,V.Yang,Nanosecond plasma enhanced H2/O2/N2premixed flat flames,Proc.Combust.Inst.35(3)(2015)3471–3478.

[14]N.L.Aleksandrov,S.V.Kindysheva,E.N.Kukaev,S.M.Starikovskaya,A.Y.Starikovskii,Simulation of the ignition of a methane–air mixture by a high-voltage nanosecond discharge,Plasma Phys.Rep.35(10)(2009)867–882.

[15]I.N.Kosarev,N.L.Aleksandrov,S.V.Kindysheva,S.M.Starikovskaya,A.Y.Starikovskii,Kinetics of ignition of saturated hydrocarbons by nonequilibrium plasma:CH4-containing mixtures,Combust.Flame 154(3)(2008)569–586.

[16]S.Nagaraja,W.Sun,V.Yang,Effect of non-equilibrium plasma on two-stage ignition of n-heptane,Proc.Combust.Inst.35(3)(2015)3497–3504.

[17]W.Sun,M.Uddi,S.H.Won,T.Ombrello,C.Carter,Y.Ju,Kinetic effects of nonequilibrium plasma-assisted methane oxidation on diffusion flame extinction limits,Combust.Flame 159(1)(2012)221–229.

[18]A.Bao,Y.G.Utkin,S.Keshav,G.Lou,I.V.Adamovich,Ignition of ethylene–air and methane–air flows by low-temperature repetitively pulsed nanosecond discharge plasma,IEEE Trans.Plasma Sci.35(6)(2007)1628–1638.

[19]I.N.Kosarev,S.V.Kindysheva,N.L.Aleksandrov,A.Y.Starikovskiy,Ignition of ethanol containing mixtures excited by nanosecond discharge above self-ignition threshold,Combust.Flame 162(1)(2015)50–59.

[20]J.Han,H.Yamashita,Numerical study of the effects of non-equilibrium plasma on the ignition delay of a methane–air mixture using detailed ion chemical kinetics,Combust.Flame 161(8)(2014)2064–2072.

[21]M.S.Bak,H.Do,M.G.Mungal,M.A.Cappelli,Plasma-assisted stabilization of laminar premixed methane/air flames around the lean flammability limit,Combust.Flame 159(10)(2012)3128–3137.

[22]T.Ombrello,S.H.Won,Y.Ju,S.Williams,Flame propagation enhancement by plasma excitation of oxygen.Part II:Effects of O2(a1Δg),Combust.Flame 157(10)(2010)1916–1928.

[23]A.Starikovskiy,N.Aleksandrov,Plasma-assisted ignition and combustion,Prog.Energy Combust.39(1)(2013)61–110.

[24]Phelps database,www.lxcat.net(retrieved on August 11,2015).

[25]IST-Lisbon database,www.lxcat.net(retrieved on August 11,2015).

[26]TRINITI database,www.lxcat.net(retrieved on August 11,2015).

[27]M.Capitelli,C.M.Ferreira,B.F.Gordiets,A.I.Osipov,Plasma kinetics in atmospheric gases,Springer,Berlin,Germany,2000.

[28]M.F.Golde,G.H.Ho,W.Tao,J.M.Thomas,Collisional deactivation of N2（A3v=0-6）by CH4,CF4,H2,H2O,CF3Cl,and CF2HCl,J.Phys.Chem.93(3)(1989)1112–1118.

[29]M.Uddi,N.Jiang,I.V.Adamovich,W.R.Lempert,Nitric oxide density measurements in air and air/fuel nanosecond pulse discharges by laser induced fluorescence,J.Phys.D.Appl.Phys.42(7)(2009)1–18.

[30]L.G.Piper,Energy transfer studies on N2（X1，v）and N2(B3Πg),J.Chem.Phys.97(1)(1992)270–275.

[31]H.Umemoto,R.Ozeki,M.Ueda,M.Oku,Reactions of N2（a′1）with H2,CH4,and their isotopic variants:Rate constants and the production yields of H(D)atoms,J.Chem.Phys.117(12)(2002)5654–5659.

[32]F.Albugues,A.Birot,D.Blanc,H.Brunet,J.Galy,P.Millet,Destruction of the levels C3Πu(v′=0,v′=1)of nitrogen by O2,CO2,CH4and H2O,J.Chem.Phys.61(7)(1974)2695–2699.

[33]I.A.Kossyi,A.Y.Kostinsky,A.A.Matveyev,V.P.Silakov,Kinetic scheme of the nonequilibrium discharge in nitrogen–oxygen mixtures,Plasma Sources Sci.Technol.1(3)(1992)207–220.

[34]G.P.Smith,D.M.Golden,M.Frenklach,N.W.Moriarty,B.Eiteneer,M.Goldenberg,C.T.Bowman,R.K.Hanson,S.Song,W.C.Gardiner Jr.,V.V.Lissianski,Z.Qin,http://www.me.berkeley.edu/gri_mech/.

[35]S.Pancheshnyi,B.Eismann,G.J.M.Hagelaar,L.C.Pitchford,Computercode ZDPlasKin,http://www.zdplaskin.laplace.univ-tlse.fr University of Toulouse,LAPLACE,CNRSUPS-INP,Toulouse,France,2008.

[36]G.J.M.Hagelaar,L.C.Pitchford,Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models,Plasma Sources Sci.Technol.14(4)(2005)722–733.

[37]A.H.Markosyan,A.Luque,F.J.Gordillo-Vázquez,U.Ebert,PumpKin:A tool to find principal pathways in plasma chemical models,Comput.Phys.Commun.185(10)(2014)2697–2702.

[38]W.C.Gardiner Jr.(Ed.),Combustion chemistry,Springer-Verlag,New York,Berlin,Heidelberg,Tokyo,1984.

[39]Y.Zhang,Z.Huang,L.Wei,J.Zhang,C.K.Law,Experimental and modeling study on ignition delays of lean mixtures of methane,hydrogen,oxygen,and argon at elevated pressures,Combust.Flame159(3)(2012)918–931.