基于Hankel矩阵的天线伺服系统辨识
2016-06-12闫少雄
闫少雄
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081 )
基于Hankel矩阵的天线伺服系统辨识
闫少雄
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081 )
天线是一个时变、非线性、复杂的动力学系统,直接建模困难较大,通常采用系统辨识的方法得到天线模型。采用伪随机序列作为辨识输入,通过解算Makov参数得到Hankel矩阵,确定模型阶次,获取天线的状态方程。对比天线模型和实际系统的响应,辨识模型准确度较高,满足工程应用的需求。
系统辨识;天线;Hankel
0 引言
天线伺服控制系统为典型的机电传动系统,模型包括电机、减速机、齿轮传动机构(或其他形式的传动)、天线转台、天线面等,电机可以通过机理建模,减速机、齿轮传递机构的机理建模涉及到刚度、阻尼等参数的合理化选取,直接机理建模比较困难,天线转台和天线面由于结构形式复杂,组件较多,采用天线的有限元分析的方法,建立天线传动链及天线座架的有限元模型,可以获取天线的模型,这种模型和天线实物存在一定的差别,适合于对天线性能进行分析,无法直接应用于伺服系统的设计[1-2]。基于模型的LQR和H∞控制器要求天线的模型必须准确,控制器设计前,必须对控制对象进行系统辨识,得到天线控制对象模型。
系统辨识建模是一种试验统计的方法,所辨识的模型是与实际过程等价的一种近似描述[7]。本文采用基于状态方程的Hankel矩阵辨识方法,通过对输入输出数据的处理,建立天线控制系统的状态方程模型。
1 辨识原理
1.1 Hankel矩阵
天线模型的离散状态方程表示形式为:
xi+1=Axi+BUi
yi=Cxi+DUi
初始状态x0为0,输入脉冲序列U0=1,Ui=0(i=1,2,…),则系统脉冲响为:
x0=0
y0=Cx0+DU0=D
x1=Ax0+BU0=B
y1=Cx1+DU1=CB
x2=Ax1+BU1=AB
y2=Cx2+DU2=CAB
(1)
x3=Ax2+BU2=A2B
y3=Cx3+DU3=CA2B
…
xk=Axk-1+BUk-1=Ak-1B
yk=Cxk+DUk=CAk-1B
定义Makov系数为:
hk=CAkB
p阶Hankel矩阵H1和H2分别为:
H1和H2矩阵内的元素都是Makov系数,H1和H2为可控性矩阵、可观测性矩阵具有如下关系:
H1=OpCp=OpR-1RCp=OnpCnp
H2=OpACp=OpR-1RAR-1RCp=OnpAnCnp
(2)
构造含有P+1个Markov系数矩阵H:
H=[DCBCAB…CAp-1B]=[h0h1h2…hp]
1.2 辨识算法
辨识时采集输入输出数据,构建输入矩阵U和输出矩阵Y如下:
根据状态方程递推关系,输入输出矩阵存在如下关系:
Y=HU
根据输入输出矩阵可求解H:
H=YU(UUT)-1
(3)
选取H矩阵中的元素得到Hankel矩阵H1和H2。
对矩阵H1进行奇异值分解,如下:
H1=VΓ2UT
(4)
其中,Γ=diag(γ1,γ2,γ3…γn),VVT=I,UUT=I。
奇异值大小代表了该状态对系统影响的重要程度,较大的奇异值之差(γk-1和γk之差)意味着系统的动态特性可以由k-1解模型表示。实际工程应用中,当奇异值很小时,对应的状态可以忽略,根据非零奇异值数量或大于某一数值的奇异值数量确定系统阶次。
系统阶次k确定后,从第一个元素开始分别取V矩阵的k列子矩阵、U的k行子矩阵和Γ的k行k列子矩阵构成新的U、V、Γ矩阵。
令P=VΓ,Q=ΓUT,可得A=P-1H2Q-1,B为矩阵Q的第一列,C为P矩阵的第一行。
2 天线辨识系统
动中通天线为多轴控制系统,通常为AE座架、AEC座架、ACE座架及XY座架等。通常将多轴控制系统分成单轴子系统,每个子系统具有一个转动轴,这些子系统既能相对独立地运行,又共同组成一个完成的整体[4]。本文辨识采用单轴子系统建模方式。
天线伺服系统辨识工作主要是进行速度环辨识,速度环包括驱动器、电机、减速机、齿轮传动机构、天线负载、码盘。
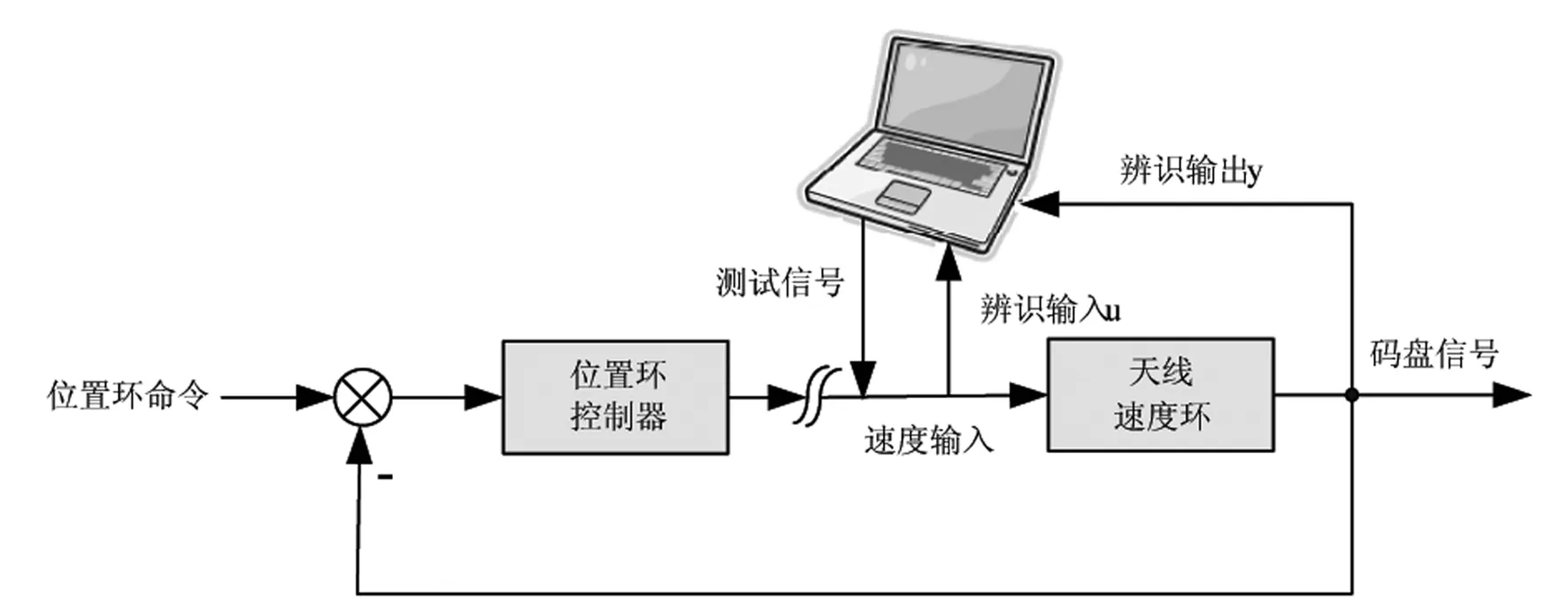
图1 天线辨识系统组成
辨识输入为天线转动角速度,输出为天线转动角度。天线转动角速度由AD5436半实物仿真机通过CAN总线发送给驱动器,天线转动角度由AD5436通过CAN总线采集并存储。
伪随机序列具有良好的随机性且其自相关性和功率谱是对白噪声的近似,能够很好地削减测量噪声对辨识的影响,是用于辨识的理想激励。伪随机序列用于系统辨识的试验信号参数有:时钟周期△t,信号长度N,重复周期数q以及信号幅度±a。天线辨识的输入信号采用伪随机序列,伪随机信号参数如表1:

表1 伪随机序列参数
采集的天线方位轴角码盘数据,经过数据处理转换成角度,辨识输入输出如图 2所示:

图2 天线方位轴辨识输入输出信号
3 辨识结果
针对0.9m动中通天线的方位轴进行辨识,根据输入输出数据解算Hankel矩阵H1,奇异值分布如图3:
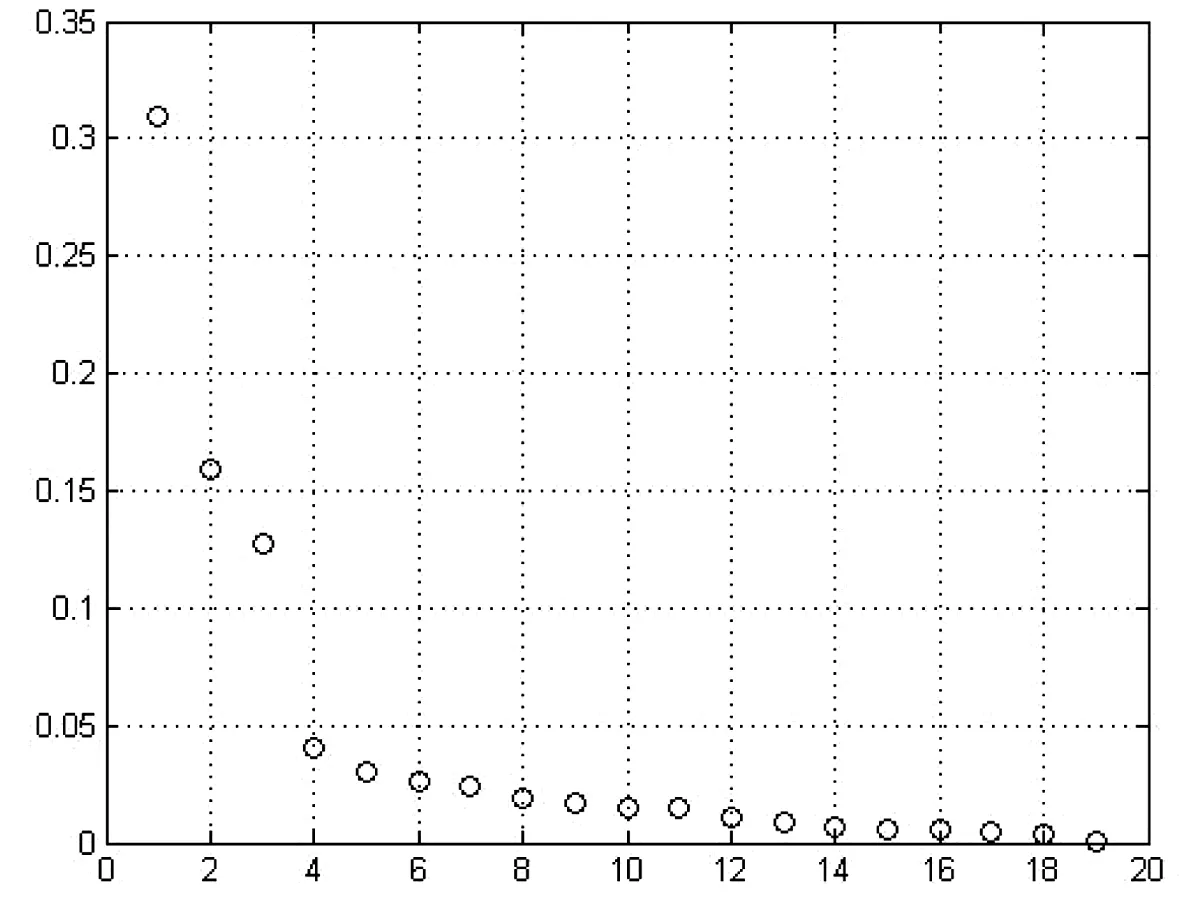
图3 奇异值分布
从第4个奇异值开始,奇异值变化不大,奇异值均小于0.05,选择待辨识系统阶次为3,辨识得到传递函数为
(5)
辨识模型的Bode图如图 4所示:

图4 辨识模型Bode图
为了验证模型的准确性,对辨识模型和试验天线给定一组同样的角速度信号,分别采集辨识模型和试验天线的输出的角度,检测辨识模型的准确度。将数据作频谱分析,天线方位轴实际的频域特性和辨识对象的频域特性如图 5所示。从图中可知,天线实际频域响应和辨识对象的传递函数在低频段和中频段有较好的吻合,高频段由于噪声、采样时间限制等影响,区别较大。

图5 辨识模型频域响应和实际系统比较
4 结束语
本文采用Hankel矩阵辨识的方法,对动中通天线进行了系统辨识,得到了天线状态空间模型,通过对比天线模型的时域和频域响应,天线模型在低频段和中频段和实际对象基本吻合,对于应用现代控制理论具有实际指导意义,为后续控制理论的应用奠定了基础。
[1] Wodek Gawronski.Modeling and Control of Antennas and Telescopes[M].Springer,Springer Science+Business Media,2008.
[2] Wodek Gawronski.Advanced Structural Dynamics and Active Control of Structures[M].Springer,Springer-Verlag New York,2004.
[3] 李白男.伪随机信号及相关辨识[M].北京:科学出版社,1987.
[4] 姜君.用于移动载体卫星通信的动中通系统若干关键问题研究[D].南京理工大学,2012.
Identification of the antenna based on hankel matrix method
YAN Shao-xiong
(The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China)
Antenna of SATCOM on the move is an time-varying,nonlinear,complex kinetics system,directly modeling is difficult, obtain antenna model is obtained by identification generally.Adopt pseudorandom sequences as input,compute Makov parameter and the Hankel Matrix,confirm the order of the system,compute the model parameters.Comparing the response of the identifiction model and the real system, the identification model has high accuracy,meet the requirements of engineering.
System identification; Antenna; Hankel
2016-12-05
1001-9383(2016)04-0041-06
TN820
A
