SK型静态混合器的液液分散数值模拟

金作宏

(河北美邦工程科技股份有限公司，河北石家庄　050035)



SK型静态混合器的液液分散数值模拟

金作宏

(河北美邦工程科技股份有限公司，河北石家庄050035)

摘要：为了对静态混合器中的液液分散过程进行深入研究，选用Euler多相流模型和k-ε湍流模型，采用计算流体力学(CFD)的方法，分别计算了单旋和四旋结构的SK型静态混合器的流场。数值模拟结果表明，液液分散过程中四旋结构产生的压降大约是单旋结构的3倍。X<0.04 m时，四旋结构湍流强度大，混合效果优于单旋结构；X>0.04 m时，单旋结构的旋转强化了对漩涡的作用，混合效果更好。研究发现，在X<0.04 m时采用四旋单元，而后采用单旋单元可以取得优秀的混合效果。

关键词：化工流体力学；静态混合器；数值模拟；压力降；不均匀系数

静态混合器是一种高效节能的化工单元设备，是将静态混合元件以一定的排列方式固定在管路中所形成的管道式混合器。这些单元借助流体自身动能，实现流体的不断分割、变形、位移和汇合，以达到良好分散和充分混合的目的[1]。静态混合器具有设备简单、无运动部件、占地面积小、维护费用低、停留时间均匀、压降低、能耗低等特点，在工业生产中应用广泛。液液两相混合是静态混合器应用的一个重要方面，可用于液液两相反应、萃取、乳化等化工过程。液液分散是两相混合的实质，其效果将直接影响后续产品的质量，因此对静态混合器中液液分散过程进行研究具有重要的实际意义。

实验手段是学者们对静态混合器中液液分散过程研究的重要方式。MIDDLEMAN[2]考察了SK型混合器混合单元长径比、物系等因素对d32的影响，并关联出了d32的表达式；龚斌等[3]对流体在SK型静态混合器中作层流流动时的流体阻力计算进行了探讨；张春梅等[4]通过实验研究了SK型静态混合器流体湍流阻力，得到了流体阻力理论计算式。随着计算机技术的快速发展，数值模拟成为流体力学研究的重要手段[5-7]。王修刚等[8]通过实验研究了液液分散过程，并对数值模拟结果进行了验证；WU等[9]采用数值模拟分析了SK型静态混合器在湍流状况下的液液分散过程。

根据FSTREIFF等[10]和THAKUR等[11]的观点，混合包括分布混合和分散混合2种基本类型，液液两相混合属于分散混合。目前，对静态混合器中液液分散的研究主要集中在分散混合性能方面。高祖昌等[12]对SK型静态混合器进行了结构优化，提出了四旋混合器结构。本文以单旋和四旋SK型静态混合器中甲苯-水两相混合为研究对象，采用数值模拟手段，分析了2种结构混合器的液液分散过程。

1数值模拟

1.1物理模型

本研究对单旋和四旋2种不同结构的SK型静态混合器进行了模拟。单旋结构单元如图1 a)所示，其直径为10 mm，高度为10 mm，厚度为0.2 mm；四旋结构单元如图1 b)所示，其直径为4 mm，高度为4 mm，厚度为0.2 mm；混合器结构如图1 c)所示。对计算模型利用GAMBIT软件进行几何建模和网格划分，全部采用四面体结构化网格。为消除网格数的影响，将几种不同尺度的网格进行对比，单旋结构生成1 219 947个网格单元，四旋结构生成1 436 925个网格单元。

图1　不同结构的SK型静态混合器Fig.1　Different structural type of SK static mixer

1.2流体

以水和甲苯为流动介质进行模拟，认为介质不可压缩，其中水作为连续相，甲苯作为分散相。水和甲苯的物理性质如表1所示，考虑到水油系统中转相点的存在[13-16]，模拟中分散相的分率选择为0.2。

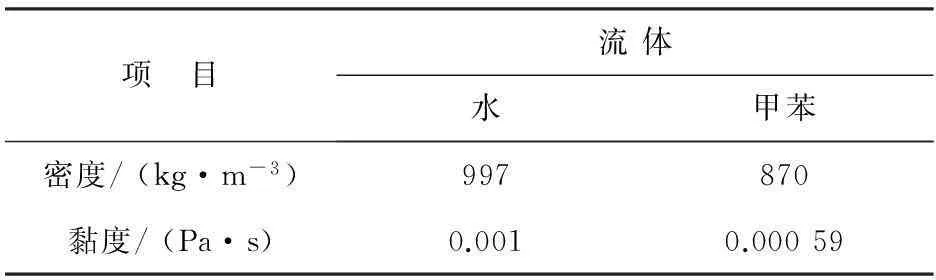
表1　模拟所用流体的物理性质

1.3模型及求解方法

采用Euler多相流模型，设水相为第一相，甲苯相为第二相。

Euler模型连续性方程为

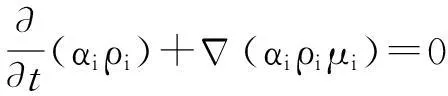
(1)

式中：αi为第i相体积分数；ρi为第i相密度分数；μi为第i相速度。

Euler模型动量方程为

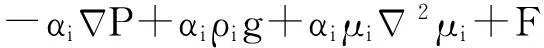
(2)

式中：μi为第i相黏度；F为相间曳力。

湍流模型选择标准k-ε模型。在Fluent6.3平台上，采用三维单精度分离解算器，压力和速度耦合项采用SIMPLE算法，体积分数方程采用QUICK格式，其余皆采用二阶迎风格式。使用速度残差作为迭代计算的监视器。

1.4边界条件

进口边界条件：采用速度进口，进口1的第二相体积分数设为1，进口2的第二相体积分数设为0，即可表示进口1全部为甲苯，进口2 全部为水。湍流特征以湍流强度和水力直径的形式输入。

出口边界条件：出口采用压力出口边界条件，压力为0 Pa。

壁面边界条件：壁面采用无滑移边界条件，壁面附近采用标准壁面函数法处理。

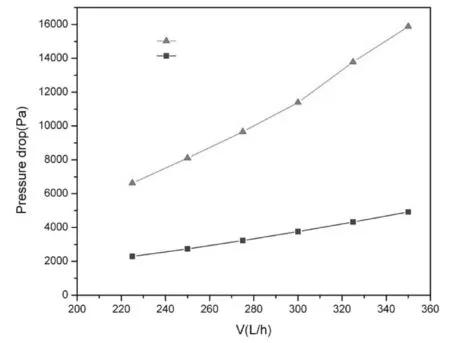
图2　液液分散过程压降与总流量的关系Fig.2　Relation of pressure drop of liquid-liquid 　　　dispersion with total flowrate

2模拟结果分析

2.1液液分散过程的压降

图2表示液液分散过程产生的压降与总流量之间的关系。由图2可知，随着总流量的增加，单旋和四旋结构液液分散产生的压降均线性增加，且四旋结构产生的压降大约是单旋结构的3倍。

2.2液液分散的混合效果

图3为模拟总流量为350 L/h所得浓度场云图。由图3可知：在进入混合单元之前，水和甲苯两相仅在界面处有少量混合；随后，两相流体在单旋和四旋混合单元的扭转和切割作用下逐渐混合均匀；在X=0.04 m (即2个单旋单元或5个四旋单元) 之前，四旋结构中两相的混合情况明显优于单旋结构，此后2种结构的混合情况相近。

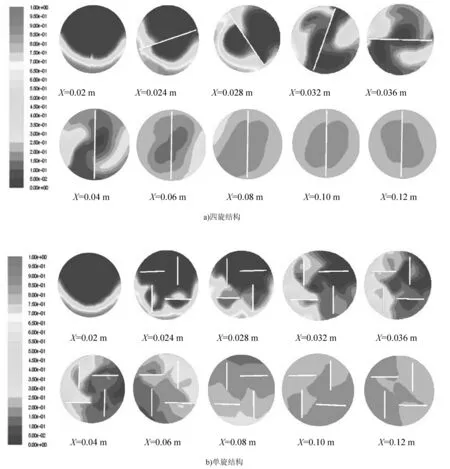
图3　浓度场云图Fig.3　Contours of concentration field

本研究进一步采用不均匀系数(COV)定量分析液液分散混合程度：

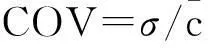
(3)

式中：

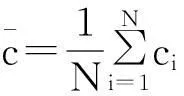
(4)

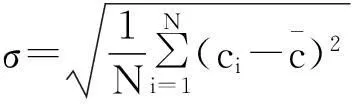
(5)

根据不均匀系数定义，COV越小表示两相混合越好，COV≤0.05时认为混合已达均匀。

图4为2种结构不均匀系数随位置的变化图。由图4可知，不均匀系数沿管长明显降低，最终水和甲苯两相近乎趋于均匀。在X=0.04m(即2个单旋单元或5个四旋单元) 之前，四旋结构中两相的混合情况优于单旋结构，此后其混合情况却比单旋结构差。

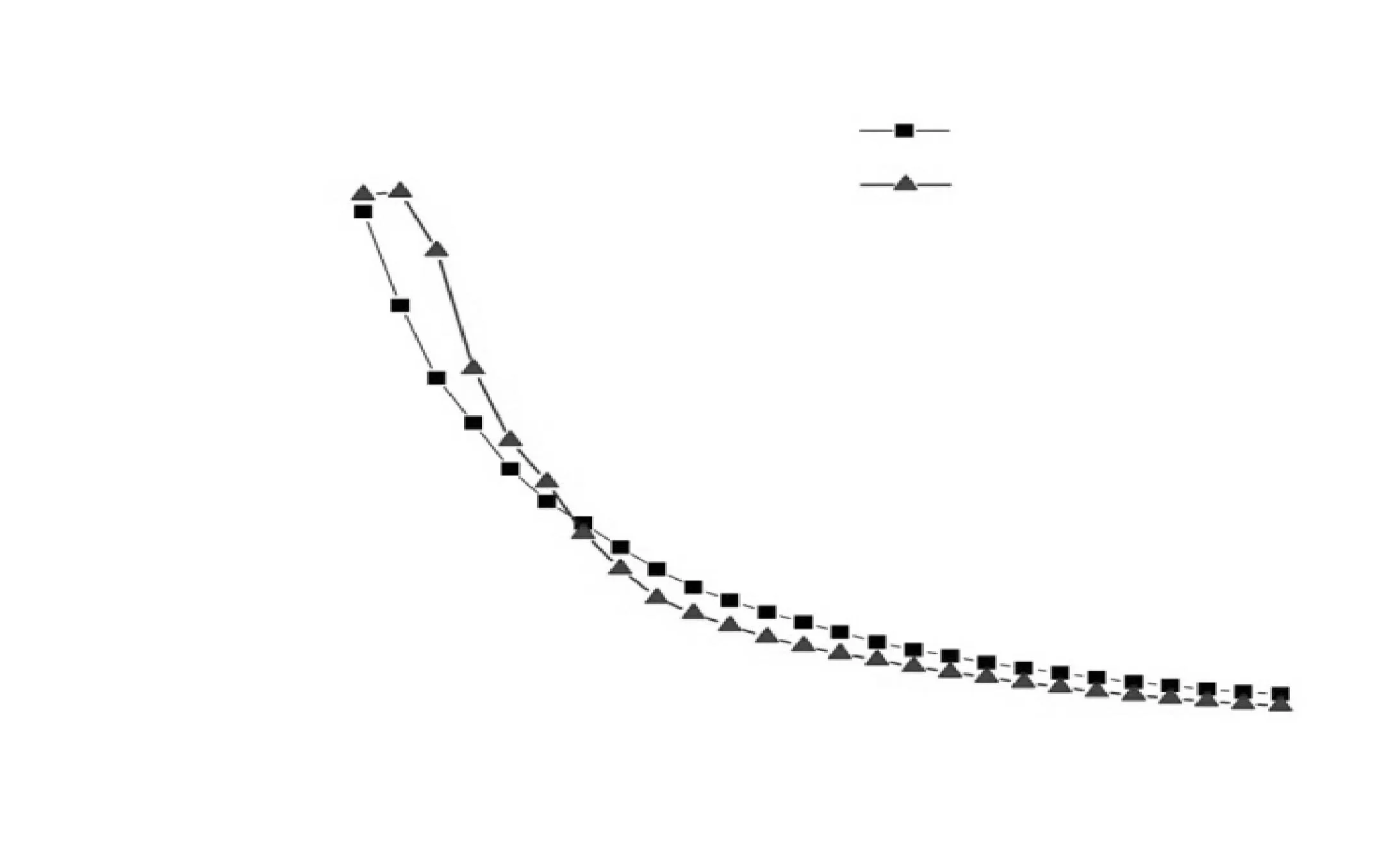
图4　2种结构的不均匀系数随　　　位置的变化关系Fig.4　Relation of COV with position of two 　　　different structures

对浓度场及不均匀系数分析可知，在X=0.04 m (即2个单旋单元或5个四旋单元) 之前，四旋结构中两相的混合情况优于单旋结构，这可能是由于四旋的复杂扭转结构有助于水和甲苯两相间的混合。此后四旋结构两相的混合情况比单旋结构差，这可能是由于四旋的复杂结构减少了流体相互混合的空间。从浓度场云图可以看出，单旋结构中浓度的不均匀位置主要集中在混合器中心区域，而四旋结构中浓度不均匀位置则随着结构单元的扭转不断变化。由此可知，四旋的复杂扭转结构在两相刚混合时有助于两相流体的混合，而后却阻碍了两相流体的混合。

2.3湍流强度

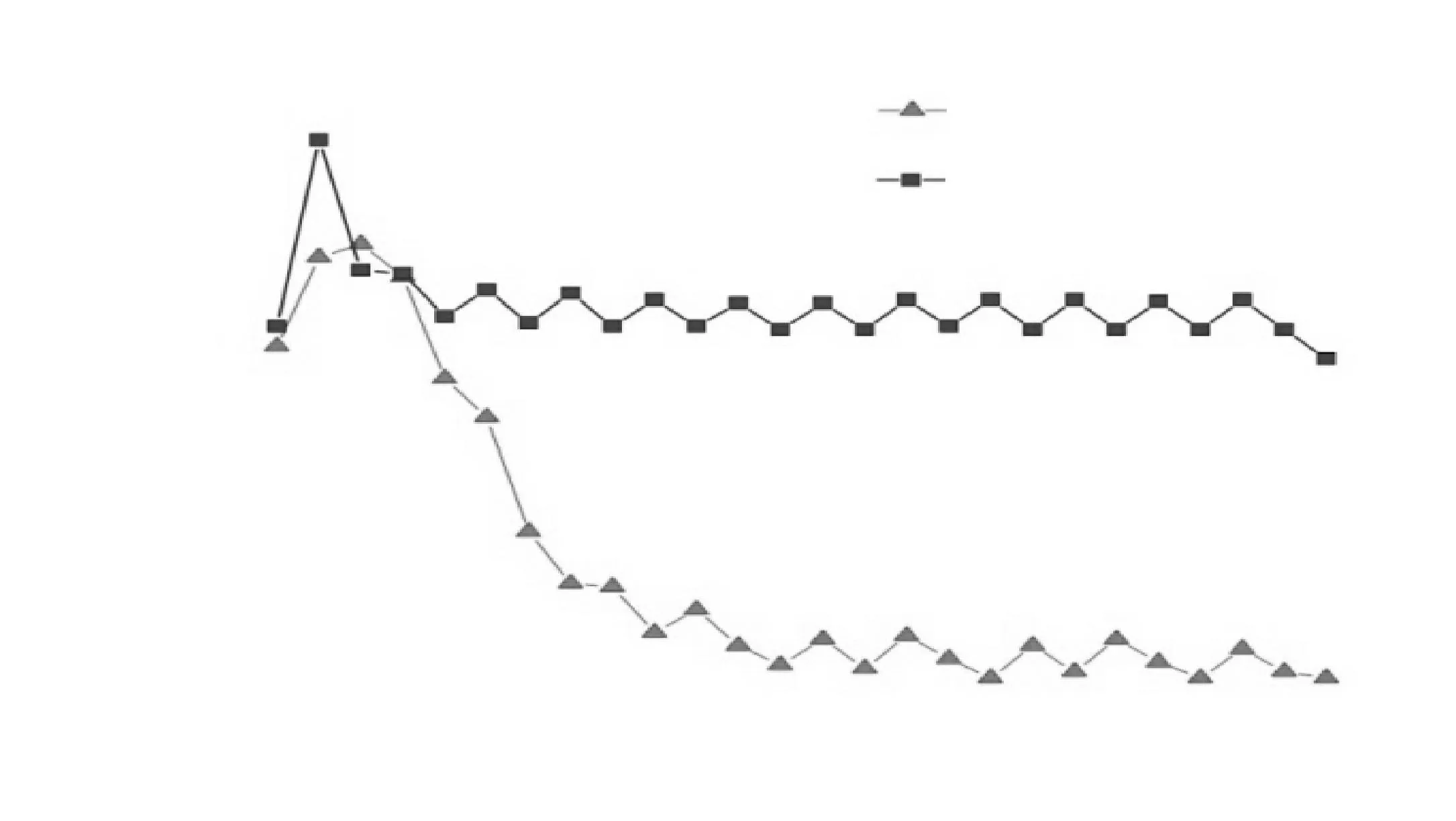
图5　2种结构的湍流强度随位置的变化关系Fig.5　Relation of turbulent intensity with 　　　position of two different structures

图5示出了模拟总流量为350 L/h所得两相的湍流强度随位置的变化关系。由图5可知，两相流体刚混合时，由于四旋结构具有复杂的扭转结构，所以其两相的湍流强度高于单旋结构，促进了两相的混合；而后单旋结构的湍流强度逐渐降低，保持在10%左右，而四旋结构的湍流强度却保持在20%左右，远大于单旋结构。

SK型静态混合器主要依靠湍流脉动扩散和漩涡发生器产生的旋转共同作用强化液液混合。单旋结构在X<0.04 m时湍流强度小，混合效率比较差；X>0.04 m时，漩涡直径仍然与漩涡发生器尺度相当(见图3 b))，所以在X>0.04 m时仍可以对漩涡产生搅拌，增强混合。而四旋结构在X<0.04 m时湍流强度大，混合效果比较好；在X>0.04 m时，漩涡直径已经比较小了(见图3 a))，漩涡发生器产生的旋转对漩涡的作用效果较差。因此，尽管四旋结构流场的湍流强度高于单旋结构，但四旋结构的混合效果却不如单旋结构。

3结语

液液分散过程中四旋结构产生的压降大约是单旋结构的3倍，其混合效果在X<0.04 m时优于单旋结构，此后其混合情况却比单旋结构差。在X<0.04 m时采用四旋单元，而后采用单旋单元，可以取得理想的混合效果。

本文对典型的液液两相体系水-甲苯系统进行了研究，所用方法及所得结论可为静态混合器的研究提供借鉴。

参考文献/References:

[1]陈敏恒, 丛德滋, 方图南, 等. 化工原理[M]. 北京: 化学工业出版社, 2007.

[2]MIDDLEMAN S. Drop size distributions produced by turbulent pipe flow of immiscible fluids through a static mixer[J]. Ind Eng Chem Process Des Develop，1974，13(1): 78-83.

[3]龚斌, 吴剑华. 流体在SK型静态混合器中作层流流动时流体阻力计算的探讨[J]. 沈阳化工学院学报, 2004, 18(4): 280-283.

GONG Bin, WU Jianhua. Study of calculating flow resistance of flowing through SK-static mixer in laminar flow[J]. J Shenyang Inst Chem Tech，2004, 18(4): 280-283.

[4]张春梅, 吴剑华, 龚斌. SK型静态混合器流体湍流阻力的研究[J]. 化学工程, 2006, 34(10): 27-30.

ZHANG Chunmei, WU Jianhua, GONG Bin. Flow resistance for SK static mixer tube of turbulent flow[J]. Chem Eng (China), 2006, 34(10): 27-30.

[5]PIANKO-OPRYCH P，JAWORSKI Z. Prediction of liquid-liquid flow in an SMX static mixer using large eddy simulations[J]. Chem Pap，2010, 64(2): 203-212.

[6]JAWORSKI Z，MURASIEWICA H. LES and URANS modeling of turbulent liquid-liquid flow in a static mixer: Turbulent kinetic energy and turbulence dissipation rate[J]. Chem Pap，2010, 64(2): 182-192.

[7]MAAB S，METZ F，REHM T，et al. Prediction of drop sizes for liquid-liquid systems in stirred slim reactors (Ⅰ): Single Stage Impellers[J]. Chem Eng J，2010, 162(2): 792-801.

[8]王修刚, 郭瓦力, 吴剑华. 静态混合器中液液分散的实验及CFD模拟[J]. 化工学报, 2012, 63(3): 767-774.

WANG Xiugang，GUO Wali，WU Jianhua. Experimental and numerical study on liquid-liquid dispersion in static mixer[J]. CIESC Journal，2012，63(3): 767-774.

[9]WU Jianhua, GUO Chengcheng, GONG Bin, et al. Numerical study of the mixing characterization in the kenics static mixer[C]//2009 Joint International Conference on Modeling and Simualtion.[S.l.]:Manchester, 2009：132-137.

[10]FSTREIFF A, MATHYS P, FISCHER T U. New fundamentals for liquid-liquid dispersion using static mixers[J]. Recents Prog Genie Procedes, 1997, 11(51): 307-314.

[11]THAKUR R K, VIAL C, NIGAM K D P, et al. Static mixers in the process industries:A review[J]. Chem Eng Res Des, 2003, 81(7): 787-826.

[12]高祖昌, 杨春花, 薛建辉, 等. 四旋混合器[P]. 中国: CN202516491U,2012-11-07.

[13]LOBRY E, THERON F, GOURDON C, et al. Turbulent liquid-liquid dispersion in SMV static mixer at high dispersed phase concentration[J]. Chem Eng Sci, 2011, 66(23): 5762-5772.

[14]翟建华.计算流体力学(CFD)的通用软件[J].河北科技大学学报,2005,26(2):160-165.ZHAI Jianhua. Review of commercial CFD software[J]. Journal of Hebei University of Science and Technology, 2005,26(2):160-165.

[15]DE B, MANDAL T K, DAS G. Experimental studies on phase inversion in a small diameter horizontal pipe[J]. Chem Eng Res Des, 2010, 88(7): 819-826.

[16]LEMENAND T, DELLAVALLE D, ZELLOUF Y, et al. Droplets formation in turbulent mixing of two immiscible fluids in a new type of static mixer[J]. Int J Multiphas Flow, 2003, 29(5): 813-840.

Numerical simulation of liquid-liquid dispersion in SK static mixer

JIN Zuohong

(Hebei Meibang Engineering Technology Company Limited， Shijiazhuang, Hebei 050035， China)

Abstract:In order to study the liquid-liquid dispersion of the static mixer, with Euler multiphase model and standard k-ε turbulent model, CFD method is used to simulate the flow field of the SK static mixer with single-turn and four-turn structure. The numerical simulation result shows that the pressure drop of four-turn structure is about triple of the pressure drop of single-turn structure in liquid-liquid dispersion. For X<0.04 m, turbulent intensity of four-turn structure is bigger than that of single-turn structure, and its mixing effect is better. For X>0.04 m, rotation effect of single-turn structure strengthens vortex, and its mixing condition is better than that of four-turn structure. Thus, four-turn structure is suggested to be applied at X<0.04 m, whereas single-turn structure at X>0.04 m.

Keywords:chemical engineering fluid mechanics； static mixer； numerical simulation； pressure drop； COV

文章编号：1008-1534(2016)03-0214-04

收稿日期：2016-01-15;修回日期：2016-03-23；责任编辑：张士莹

基金项目：科技型中小企业技术创新基金无偿资助项目(12C26211300743)

作者简介：金作宏(1971—)，男(满族)，辽宁营口人，高级工程师，硕士研究生，主要从事精细化工方面的研究。E-mail:jinzuohong@163.com

中图分类号：TQ028.8

文献标志码：A

doi:10.7535/hbgykj.2016yx03006

金作宏.SK型静态混合器的液液分散数值模拟[J].河北工业科技,2016,33(3):214-217.

JIN Zuohong.Numerical simulation of liquid-liquid dispersion in SK static mixer[J].Hebei Journal of Industrial Science and Technology,2016,33(3):214-217.