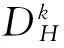集值微分方程初值问题的高阶收敛性
2016-06-12王培光刘会娜
王培光,刘会娜
(1.河北大学 电子信息工程学院,河北 保定 071002;2.河北大学数学与信息科学学院,河北保定 071002)
集值微分方程初值问题的高阶收敛性
王培光1,刘会娜2
(1.河北大学 电子信息工程学院,河北 保定071002;2.河北大学数学与信息科学学院,河北保定071002)
摘要:通过应用比较原理和拟线性方法,对所构造的单调迭代序列进行了分析,证明了其逼近解序列一致且高阶收敛于该问题的解,所得结论推广和改进了已有的研究成果.
关键词:集值微分方程;拟线性化方法;高阶收敛
MSC 2010:34D20;34A37
近年来,定义在半线性度量空间上的集值微分方程的研究引起了国内外学者的广泛关注[1-7],这些结果多为解的稳定性问题的研究工作[1-4].关于集值微分方程解的收敛性结果相对较少[5-6],特别是关于解的高阶收敛性的结果未见报道.Lakshmikantham[8]系统地总结了拟线性化方法在常微分方程中的应用,并相继有学者讨论了常微分方程和分数阶微分方程初边值问题解的快速收敛性[9-11].本文应用拟线性化方法,讨论一类集值微分方程初值问题.通过应用比较原理和拟线性方法,对所构造的单调迭代序列进行分析,给出其逼近解序列一致且高阶收敛于该问题解的判定准则.所得结论推广了已有的研究成果.
1预备知识
首先给出如下关于集值的定义[7]151.
设K(Rn)(Kc(Rn))是Rn上的所有非空紧集(紧凸集)的集合,定义Hausdoff度量

D[A+C,B+C]=D[A,B],D[A,B]=D[B,A],
D[λA,λB]=λD[A,B],D[A,B]≤D[A,C]+D[C,B],
其中A,B,C∈Kc(Rn),λ∈R+.
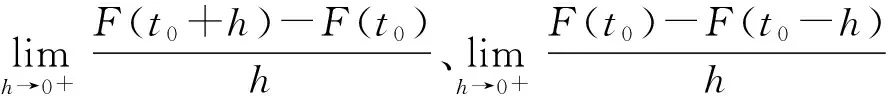
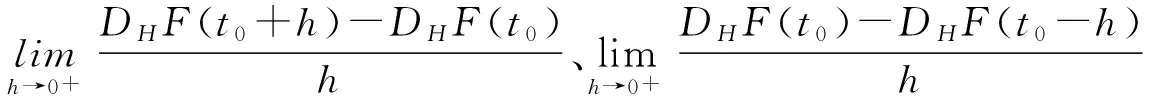


考虑如下集值微分方程
(1)
其中F∈C[I×Kc(Rn),Kc(Rn)].
如果存在映射U∈C1[I,Kc(Rn)],I=[t0,t0+a],a>0满足式(1),则称U是式(1)的解,与式(1)等价的积分形式为
因此初值问题(1)的解又可以写成Hukuhara积分
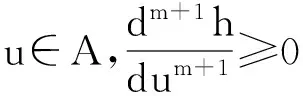
为得到本文主要结果,给出如下引理.
引理1[7]153假设
A1)V,W∈C1[I,Kc(Rn)],F∈C[I×Kc(Rn),Kc(Rn)],对于任意t∈I,F(t,X)关于X单调非减,并且DHV≤F(t,V),DHW≥F(t,W),t∈I.
A2)对任意的X,Y∈Kc(Rn),X≥Y,t∈I,F(t,X)≤F(t,Y)+L(X-Y),其中L为大于零的常数.
A3)V(t0)≤W(t0),则V(t)≤W(t),t≥t0.
引理2[8]5假设V,W∈C1[I,Kc(Rn)],F∈[Ω,Kc(Rn)],DHV≤F(t,V),DHW≥F(t,W),t∈I,且V≤W,V(t0)≤U0≤W(t0),其中Ω={(t,U)∶V(t)≤U(t)≤W(t),t∈I},则方程(1)存在解U且满足V≤U≤W.

2主要结果
本节利用拟线性化的方法,减弱基本结论中对F(t,U)在U,t∈I上的凸凹性要求,分2种情况讨论初值问题(1)的高阶收敛问题.


(2)

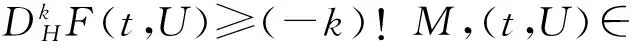
(3)
令
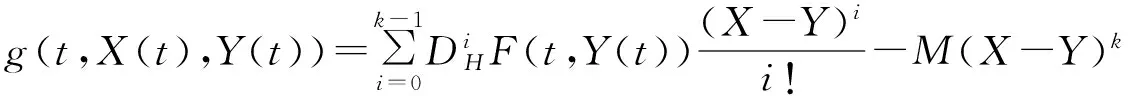
(4)
由式(3)可得g(t,X(t),Y(t))≤F(t,Y(t)),t∈I,其中V(t)≤Y≤X≤W(t).
首先考虑初值问题
(5)
注意到DHW(t)≥F(t,W(t))≥g(t,W(t),V(t)),W(0)≥U(0),t∈I,并且有DHV(t)≤F(t,V(t))=g(t,V(t),V(t)),V(0)≤U(0),t∈I.注意到由F(t,U)+MUk在U,t∈I上是k-1超凸及均值定理得到g(t,U1,V(t))-g(t,U2,V(t))≤L2(U1-U2),其中L2>0,V≤U2≤U1≤W.所以V,W分别是初值问题(5)的下解和上解.进而由引理1和引理2可知,初值问题(5)存在解V1使得V≤V1≤W.
不妨假设有序列V≤V1≤…≤Vn≤W.考虑
(6)
其中Vn为初值问题(6)的解.
(7)
注意到DHW(t)≥F(t,W(t))≥g(t,W(t),Vn(t)),W(0)≥U(0)和DHVn(t)=g(t,Vn(t),Vn-1(t))≤F(t,Vn(t))=g(t,Vn(t),Vn(t)),Vn(0)≤U0,所以Vn(t),W(t)是初值问题(7)的下解和上解.进而由引理1和引理2,初值问题(7)存在解Vn+1使得Vn≤Vn+1≤W.因此{Vn}为一单调非减序列且在C1[I,Kc(Rn)]上是一致有界的,且{Vn}满足DHVn=g(t,Vn,Vn-1),Vn(0)=U0,又注意到对任意的s 因而{Vn}是等度连续的,从而由Ascoli定理可得,{Vn}有一致收敛的子序列.又由于{Vn}是单调非减序列,则{Vn}一致收敛.从而在C1[I,Kc(Rn)]上{Vn}收敛到连续函数ψ∈[V,W].由于初值问题的等价积分形式是 所以 因此,ψ是初值问题(1)的解. 下证该收敛是k阶的.由式(2)可得 其中ρn∈[Vn,ψ].另一方面,由式(4)及式(7)可得 令en=ψ-Vn,αn=Vn+1-Vn,有 进一步可得‖Vn+1-ψ‖≤λ‖Vn-ψ‖k.即{Vn}为k阶收敛. 同理,可构造序列{Wn}.令V(t)≤X≤Y≤W(t),对任意给定的t∈I,有 (8) 令 (9) 注意到W0=W,对于n≥1,由归纳定义出Wn为下面初值问题的解 (10) 由此可得V≤Wn≤…≤W2≤W1≤W.因此{Wn}为单调非增序列且在C1[I,Kc(Rn)]上是一致有界的,且{Wn}满足DHWn=h(t,Wn,Wn-1),Wn(0)=U0,又由式(7)、(10)可得DHVn(t)=g(t,Vn(t),Vn-1(t))≤F(t,Vn(t)),Vn(0)≤V0.DHWn(t)=h(t,Wn(t),Wn-1(t))≥F(t,Wn(t)),Wn(0)≥V0.由引理1得Vn(t)≤Wn(t).即V≤V1≤…≤Vn≤…≤W2≤W1≤W,又注意到对任意的s 因而{Wn}是等度连续的,从而由Ascoli定理可得,{Wn}有一致收敛的子序列,又由于{Wn}是单调非增序列,则{Wn}一致收敛.这样单调序列{Vn}、{Wn}在I上一致收敛于方程(1)的唯一解.从而在C1[I,Kc(Rn)]上{Wn}收敛到连续函数ψ∈[V,W].由于初值问题的等价积分形式是 所以 因此,ψ是初值问题(1)的解. 下证收敛是k阶的.由式(8)可得 其中τn∈[ψ,Wn].另一方面,由式(9)及式(10)可得 令fn=ψ-Wn,bn=Wn+1-Wn,有 其中 由引理3得 进一步可得‖ψ-Wn+1‖≤λ‖ψ-Wn‖k.即{Wn}为k阶收敛.定理证毕. 对于F(t,U)-MUk在U,t∈I上是k-1超凹的情况,有如下结论. (11) (12) 令 (13) 由式(12)可得g(t,X(t),Y(t))≤F(t,X(t)),t∈I,其中V(t)≤Y≤X≤W(t). 考虑初值问题 (14) 以下证明与定理1类似可证,故略. 参考文献: [1]BHASKAR T G,LAKSHMIKANTHAM V.Set differential equations and flow invarianee[J].Appl Anal,2003,82:357-368.DOI:10.1080/0003681031000101529. [2]BHASKAR T G,LAKSHMIKANTHAM V.Lyapunov stability for set differential equations[J].Dynam Systems Appl,2004,13:1-10. [3]LAKSHMIKANTHAM V,LEE S,VATSALA A S.Set-valued hybrid dilfferential equations and stability in terms of two measures[J].J Hybrid Syst,2002,2:169-187. [4]LAKSHMIKANTHAM V,LEE S,VATSALA A S.Interconneetion between set and fuzzy differential equations[J].Noulinear Anal,2003,54:351-360.DOI:10.1016/S0362-546X(03)00067-1. [5]王培光,高纬.集值微分方程初值问题拟线性化方法[J].河北大学学报(自然科学版),2011,31(1):1-6. WANG Peiguang,GAO Wei.Quasilinearization of initial value problem for set differential equations[J].Journal of Hebei University(Natural Science Edition),2011,31(1):1-6. [6]WANG P G,GAO W.Quasilinearization of an initial value problem for a set valued integrodifferential equation[J].Computers and Mathematics with Applications,2011,61:2111-2115.DOI:10.1016/j.camwa.2010.08.084. [7]WANG P G,HOU Y.Generalized quasilinearization for the system of fractional differential equations[J].J Funct Spaces Appl,2013:793263. [8]LAKSHMIKANTHAM V,VATSALA A S.Generalized quasilinearization for nonlinear problems[M].Dordrecht:Kluwer Academic Publishers,1998. [9]MELTON G T,VATSALA A S.Generalized quasilinearization and higher order of convergence for first order initial value problems[J].Dynamic Synamic Systems and Applications,2006,15:375-394. [10]王培光,侯颖,刘静.一类分数阶微分方程的广义拟线性化方法[J].河北大学学报(自然科学版),2011,31(5):449-452. WANG Peiguang,HOU Ying,LIU Jing.Generalized quasilinearization for fractional differential equations[J].Journal of Hebei University(Natural Science Edition),2011,31(5):449-452. [11]KALABA R E,MOHAPATRA R N,VAJRAVELU K,et al.Extension of the method of quasilinearization and rapid convergence[J].Journal of Optimization Theory and Applications,1998,96:667-682. (责任编辑:王兰英) Higher order convergence for set differential equations with initial conditions WANG Peiguang1,LIU Huina2 (1.College of Electronic and Information Engineering,Hebei University,Baoding 071002,China;2.College of Mathematics and Information Science,Hebei University,Baoding 071002,China) Abstract:By using the comparison principle and the method of quasilinearization,two monotone iterative sequences of approximate solutions which converge uniformly and higher order to the solution of the problem were obtained.The results generalize and improve the known ones. Key words:set differential equations;quasilinearization;higher order convergence DOI:10.3969/j.issn.1000-1565.2016.01.001 收稿日期:2015-11-17 基金项目:国家自然科学基金资助项目(11271106);河北省自然科学基金资助项目(A2013201232) 中图分类号:O175.12 文献标志码:A 文章编号:1000-1565(2016)01-0001-06 第一作者:王培光(1963—),男,黑龙江哈尔滨人,河北大学教授,博士生导师,主要从事微分方程与控制理论的研究. E-mail:pgwang@hbu.edu.cn