微重力模拟育种平台运动轨迹的规划研究

吕雨鑫，李伟凯，董晓威（黑龙江八一农垦大学信息技术学院，大庆163319）



微重力模拟育种平台运动轨迹的规划研究

吕雨鑫，李伟凯，董晓威
（黑龙江八一农垦大学信息技术学院，大庆163319）

摘要：在三维空间气浮式模拟微重力育种平台装置的设计中，为了达到控制育种装置的空间运动姿态的目的，就要通过对育种平台运动轨迹进行规划来推导出其运动控制方程，实现电机伺服系统在三自由度上的联动问题，以及气缸在垂直方向上的伸缩位移量问题。这两者协调运动才能使平台按照预先设定的椭圆形轨迹运动。

关键词：运动姿态；电机联动；椭圆形轨迹

黑龙江垦区既是我国重要的商品粮基地，也是全国最大规模的国有农场集群经济区，经过多年的发展建设，垦区自从2006以来其农业现代化发展水平指标已连续八年实现了历史性突破[1]。近几年在航天技术迅速发展的基础上，空间农业成为了农业发展的一个新趋势，但是由于耗资巨大、实验条件有限、环境条件不好控制等问题的存在，使其发展受到很大的制约，因此人们一直致力于研究此类问题的解决办法。随着科学技术的不断发展，人们把空间实验转移到了地面进行实验研究，利用地面的设备来模拟复杂的空间环境条件，这样不仅可以很好的控制实验条件、重复多次试验还大大节约了成本，提高了经济效益。以往人们大多使用的是水平回转器作为地面模拟仪器，但是其只适用于平面二维，为了弥补回转器模拟效果不好、控制精度较低等因素的影响，采用气浮法在三维空间内进行微重力模拟实验[2]。因此在此基础之上创新的设计研究在地面进行空间微重力环境模拟实验的育种装置。规划育种平台的运动轨迹，控制育种装置的空间姿态。

1　微重力模拟育种平台椭圆形轨迹数学模型

微重力模拟育种平台主要由机械和控制两大部分组成。在实际工作中机构实现预定轨迹的运动不仅与机构的几何尺寸有关，而且与控制方法和控制器性能有关[3]。要使平台按照预先设定的轨迹来进行运动，就要控制电机3个自由度上各轴联动问题，同时还要控制垂直方向上所使用气缸运动的伸缩位移量。两者的协调配合才能使平台按既定的轨迹运动。控制系统框图如图1所示。

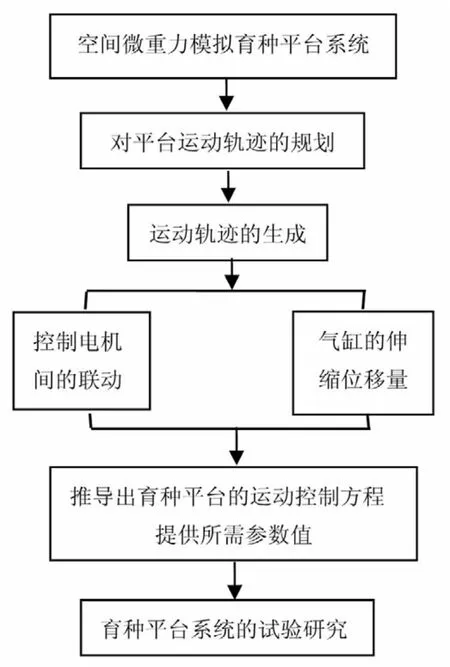
图1　微重力育种平台的运动控制系统框图Fig.1Diagram of motion control system on microgravity breeding platform

运动轨迹是实体运动在空间中的表现，是指育种平台在运动过程中的位移、速度和加速度。分析运动的基本特征对于分析运动轨迹而言是有价值的[4]。在椭圆形轨迹自动旋转过程中，根据轨迹的数学模型可以规划出平台的初始运动轨迹[5]。在实际的运行过程中，再根据实际情况对初始运动轨迹做出修正，最终实现轨迹的闭环反馈控制。其中椭圆形横截面轨迹的数学模型如下图2所示。

图2　育种平台椭圆形横截面运动轨迹的数学模型Fig.2Mathematical model of elliptical cross-section trajectory on breeding platform

由图可知，由3段圆弧拟合而成的1/4平面椭圆形曲线的方程分别为：

当（90°-θ1<θ≤90°）时：

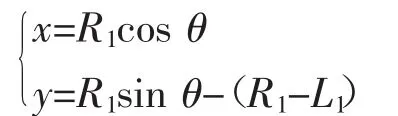
当（0°≤θ<θ2）时：

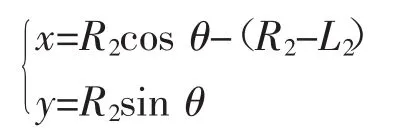
当（θ2≤θ≤90°-θ1）时：

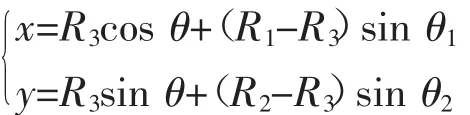
而椭圆形轨迹四个角上的曲率中心可表示为：

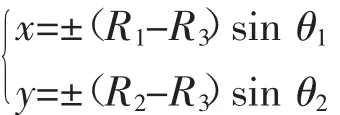
由此可知上、下、左、右四边的曲率中心分别为（0，L1-R1）、（0，R1-L1）、（R2-L2，0）、（L2-R2，0）。

2　微重力模拟育种平台运动速度的控制

根据以上推导出的1/4平面内的椭圆形曲线方程，可知在Σo=[o；x，y]坐标系中，随着椭圆形轨迹的运行过程中轨迹的初始切入点P的位置坐标和时间的关系如下：

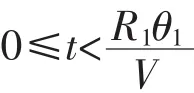
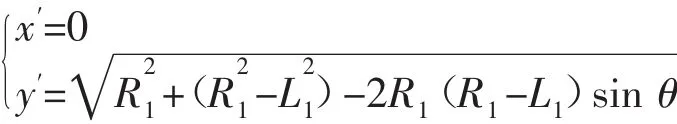
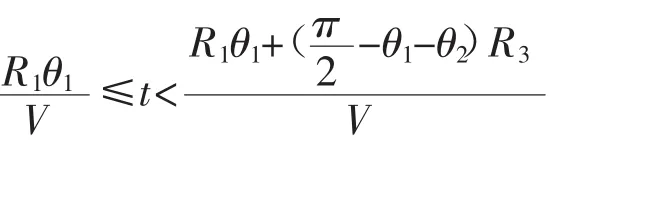
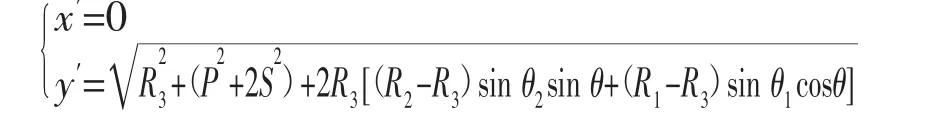
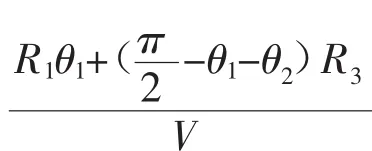
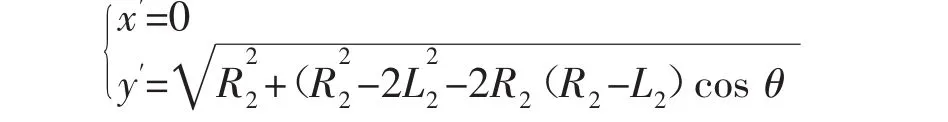
但是为了确保平台在运动过程中速度能够保持恒定，就需要时刻调整育种平台的旋转速度，以保证其与初始运动轨迹接入点P处的线速度能够保持恒定。根据平台的轨迹规划方程及相应的几何变换可得出旋转角速度随时间变化的数学模型，如下图3所示：

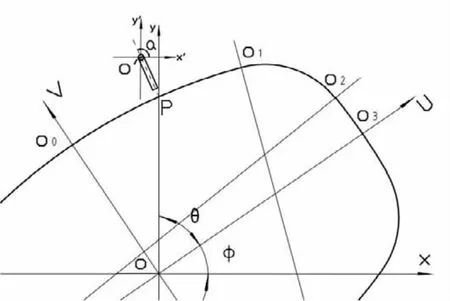
图3　微重力模拟育种平台运动的数学模型Fig.3Mathematical model of breeding platform motion on microgravity simulation

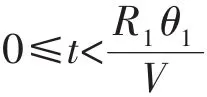
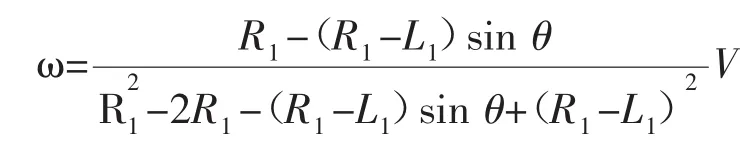
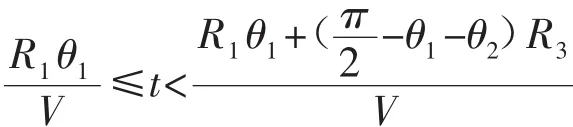
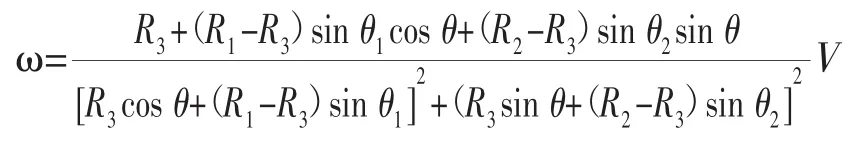
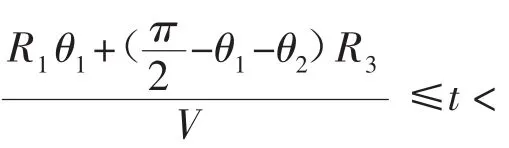
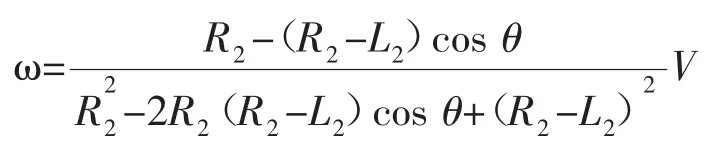
以上椭圆形轨迹模型的建立只是为实际的微重力育种平台运行过程提供了一个初始预设的运动轨迹模型，在实际操作过程中还需要根据检测机构所测出的检测值对其进行实时的修正。

因为平台在按预设轨迹运行过程中弧长是保持恒定的，所以可知在检测机构的坐标系Σo'=[o'；x'，y']中，平台的起始端点位置处与轨迹运行初始点P处的坐标变换为：

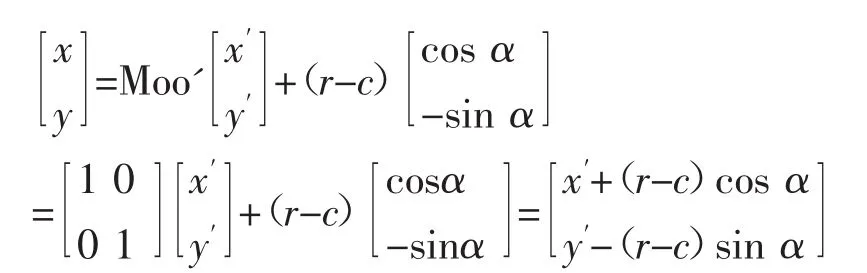
根据以上运动的数学模型可以得出，育种平台的姿态角：

α=θ+φ

其中φ表示平台按照逆时针方向旋转的角度，并且在不同的弧内φ与θ存在着一定的对应关系。

3　微重力模拟育种平台运动轨迹的规划

由于椭圆形截面的几何形状不匀称性，在椭圆形轨迹自动运行过程中，平台的高度、姿态角和水平位置都会随着轨迹的变化而相应的调整。在实际应用中要使育种平台按照一定得速度回转，那么回转中心就可视为几何中心[6]。采用伺服电机作为驱动电机，在控制的过程中通过调节伺服电机的转速来保证育种平台旋转速度的恒定[7]。所以，设平台在运动平面的全局笛卡尔坐标系为Σo=[o；x，y]，P为轨迹的初始位置点，θ为曲线的参数，此时平台的姿态角为α，椭圆形轨迹旋转φ角度后的坐标系为Σo=[o；U，V]，若旋转速度为v，则可得出1/4平面的椭圆旋转过程中育种平台的运动轨迹规划如下为：

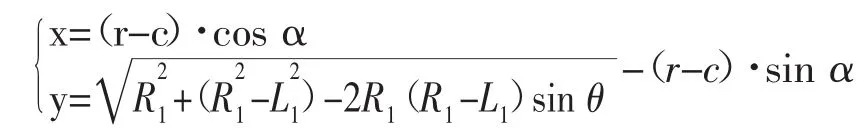
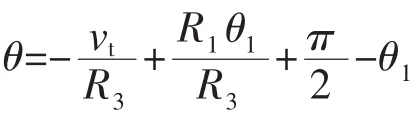
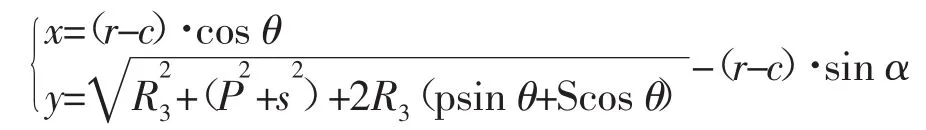
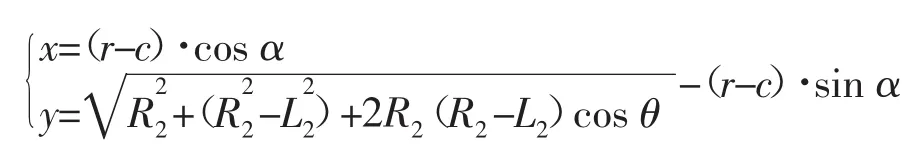
由于椭圆形具有对称性，根据1/4的运动方程就可推导出其余3/4平面的运动轨迹规划方程。

4　结论

根据研究微重力模拟育种平台的运动轨迹的规划问题，设计育种平台是按照预先规划的椭圆形轨迹来运动的，以此来完成对其在空间中运动姿态的控制。但是研究只是提供了一个微重力模拟育种平台在运行过程中初始预设的运动轨迹模型，为了能够验证模型是否可以真的实现，还需要在实际操作过程中根据检测机构所测出的检测值对其进行实时的修正。因此，实时修正的部分是日后进一步研究的内容。

参考文献：

［1］王一夫，王新利.黑龙江垦区农业现代化发展水平分析［J］.黑龙江八一农垦大学学报，2014，26（1）：99-104.

［2］胡文瑞.微重力科学概论［M］.北京：科学出版社，2010.

［3］高岩.工业机器人轨迹规划算法的研究与实现［D］.沈阳：中国科学院，2014.

［4］李达.工业机器人轨迹规划控制系统的研究［D］.哈尔滨：哈尔滨工业大学，2011.

［5］张忠厚，李发跃.椭圆形焊缝全自动埋弧焊装置的设计［J］.焊接技术，1990，32（4）：33-39.

［6］金明新.罐体椭圆截面的近似画法及计算方法［J］.专用汽车，1995，2（8）：29-31.

［7］钱平.伺服系统［M］.北京：机械工业出版社，2005.

Planning of Breeding Platform Trajectory on Microgravity Simulation

Lv Yuxin，Li Weikai，Dong Xiaowei
（College of Information and Technology，Heilongjiang Bayi Agricultural University，Daqing 163319）

Abstract:To design the three-dimensional analog of breeding platform device on flotation microgravity，it was necessary to elicit the equation of motion control through trajectory plan of breeding platform to control the breeding unit’s space motion gesture.This could resolve linkage problem of motor servo system in three degrees of freedom，as well as figure out the amount of cylinder stretching displacement in vertical direction.The platform worked in accordance with preset elliptical trajectory when they had the coordinated motion.

Key words：athletic stance；motor linkage；oval track

中图分类号：Q78

文献标识码：A

文章编号：1002-2090（2016）01-0084-04

doi:10.3969/j.issn.1002-2090.2016.01.019

收稿日期：2014-12-20

基金项目：国家自然基金项目（E201132）。

作者简介：吕雨鑫（1989-），女，黑龙江八一农垦大学信息技术学院2013级硕士研究生。

通讯作者：李伟凯，男，教授，博士研究生导师，E-mail：bynd@263.net.cn。