《相似三角形的性质》教学设计

张建南

中图分类号：G633.6 文献标识码：B 文章编号：1672-1578（2016）05-0394-01

【设计意图】：

本课是华师大版九年级上"相似形"一章的重要内容之一，是在学生学完相似三角形的定义及判定的基础上进一步研究相似三角形的特性以完成对相似三角形的全面研究，它是全等三角形性质的拓展，在圆中有着广泛的应用。同时，相似三角形的性质也是解决有关实际问题的重要工具，根据教学大纲的要求考虑到初三学生的年龄特点和心理水平将理解相似三角形的性质作为本节重点而将探究推导性质作为本节难点。本课通过学生动手作图，探究发现结论，体验成功的乐趣，培养学生探究问题的科学态度，促进创造性思维的发展，使学生尝到学习几何的乐趣，体会到实验几何，快乐几何。同时采用探究性学习方法自主地感受新知，将新知识纳入自己的认知结构中成为有效的知识。

【教学目标】：

（1）探索、归纳并掌握相似三角形对应线段（高、中线、角平分线）比、周长比、面积比与相似比之间的关系，掌握定理的证明方法；提高分析，推理能力。

（2）对性质定理的探究学生经历类比——猜想——论证——归纳的过程，培养学生主动探究、合作交流的习惯和严谨治学的态度，并在其中体会类比的数学思想，培养学生大胆猜想、勇于探索、勤于思考的数学品质，提高分析问题和解决问题的能力。

（3）在学习和探讨的过程中，体验特殊到一般的认知规律；通过学生之间的交流合作，在合作中体验成功的喜悦，树立学习的自信心。

【教学重点】：理解相似三角形的性质。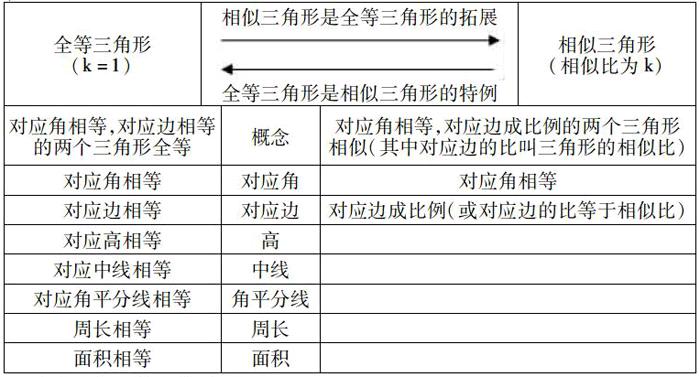

【教学难点】：相似三角形性质定理的探索及推导

【教学过程】：

1.复习提问，温故而知新

请同学们以小组为单位共同回忆以下内容：

（1）.相似三角形与全等三角形的概念及关系；

（2）.全等三角形的性质及已学过的相似三角形的性质；

（3）.利用已有的全等三角形性质，你能推出全等三角形还有哪些性质。

2.实践交流，探索新知

问题1：类比全等三角形的性质，想一想可以从哪几个方面继续研究相似三角形的性质；

从相似三角形对应线段（对应高、对应中线、对应角平分线）、周长及面积继续研究相似三角形的性质。

你是怎么想到这几个方面？主要是类比全等三角形的性质。

问题2：猜一猜，相似三角形还有哪些性质（分别用文字语言与符号语言表示，用符号语言表达时，要画图形）。

性质一：相似三角形对应高、对应中线、对应角平分线以及它们的周长的比等于相似比。

也可能有学生会提出其他错误的结论（如对应高、角平分线、中线相等；面积比等于相似比等），教师暂时不点破，由学生自己去证明后推翻原有的错误结论。

教师提问：你是怎么想到这几方面性质的？

学生回答后教师总结：猜想有类比猜想、归纳猜想（从特殊到一般）及逻辑推理等。

问题3：小组成员分工论证你们得到的猜想（每个同学至少证明其中一个命题）；或推翻、修正猜想，再论证。

这一阶段是本课的重点，主要是先由学生小组分工完成，可能是证明了正确的结论，也可能是推翻了之前的错误，教师主要是展示学生的成果，并给出适当的点评。

归纳出证明步骤：画图、写已知求证，证明

归纳出证明方法：大三角形相似小三角形相似结论

完成了以上两个探索三个问题之后由师生共同总结出：

性质一：相似三角形对应高、对应中线、对应角平分线以及它们的周长的比等于相似比。

性质二：相似三角形的面积比等于相似比的平方。

3.巩固练习，加深理解

3.1已知两个相似三角形一对对应中线的长分别是2cm和5cm，那么它们的相似比为________，对应高的比为_______，如果一对对应角平分线中较短的为3.6cm，则较长的为________。

3.2两个相似三角形对应高的比为7：5。其中一个三角形的周长为70cm，则另一个三角形的周长为________，若其中一个三角形的面积为490 ，则另一个三角形的面积为________.

3.3已知：如图，DE∥BC，AB=30m，BD=18m，△ABC的周长为80m，面积为100m2，

求△ADE的周长和面积？过E作EF∥AB交BC于F，其他条件不变，则△EFC的面积等于多少？平行四边形BDEF的面积为多少？ （写出解答过程）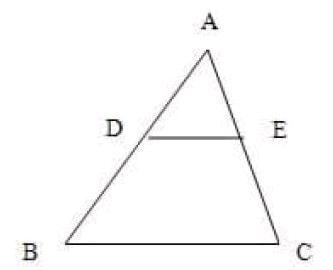

4.回顾反思，畅谈心得

本节课你有何收获？

（1）相似三角形对应高、对应中线、对应角平分线的比及周长比等于相似比。

（2）相似三角形的面积比等于相似比的平方。

（3）对性质定理的探究我们经历：猜想——论证——归纳的过程，其中猜想包括：类比猜想、归纳猜想（从特殊到一般）及逻辑推理。

论证的过程包括：画图，写已知求证，证明等步骤。

5.学以致用，作业布置

必做题：

（1）书本P81：习题第2题

（2）先画出一个边长分别为1、2、3的三角形，然后作出一个面积是它4倍的三角形。

选做题：同步练习P31

【板书合计】：

【课后反思】：本课的教学设计从学生原有的认知出发，通过设置有效问题串，引导学生回忆旧知并建立它们之间的联系，进而以类比思想为主线，从高、中线、角平分线、周长、面积切入，展开相似三角形的性质的探究学习，让学生经历从猜想到论证，最后得出正确结论的过程，体现合情推理与逻辑推理的有机结合。重视学生用文字语言、图形语言、符号语言表述数学结论、论证数学结论的规范性，进一步培养学生的语言表达能力。充分发挥学生的主体性，在生生、师生的互动生成过程中，让学生充分发表自己的见解，展示自己的探索成果，从而形成良好的课堂学习氛围。设计分层次的课堂练习与作业，使不同层次的学生能解答他们力所能及的问题，在原有的基础上得到发展。