活用变式教学对培养学生思维的意义
2016-06-12杜继刚
杜继刚
中图分类号:G648 文献标识码:B 文章编号:1672-1578(2016)05-0361-02
一直以来,几何的教学是中学数学教学的重点也是难点,它有美丽的图形、巧妙的思维、严密的逻辑结构,具有典型的数学美,最能培养人的创造性思维能力。而变式教学可以很好地深化课堂教学效果,发展学生数学思维能力。
1.何谓变式教学
所谓"变式教学",是指"以培养学生灵活转换、独立思考能力为目的,在课堂教学过程中教师精心设计一些不断变更问题情景或者改变思维角度,由简到繁、由易到难的数学问题,使事物的非本质特征时隐时现,而事物的本质特征却始终保持不变的教学形式"。这是一种把学生的思维逐渐引向新的高度的一种教学方法,它实际上是教师有目的地通过"变式"为学生组织了一个引导思维的活动。在这样的教学活动中,"变式"的含义是指变化形式,这里的"形式"可以是知识形成过程中的问题设计、基本概念、定理、公式、例题等具体形式,也可以是如教法、学法等抽象形式。
2.变式教学与培养学生创造性思维的关系
创造性思维是创新能力的核心内容之一。创造性思维的重要品质主要有:独创性、严谨性、发散性、批判性和深刻性、灵活性和敏捷性等。变式教学为培养创造性思维提供了最好的土壤。合理的设计题组,进行变式教学,有助于学生加深对知识的巩固与深化,提高解题技巧及分析问题、解决问题的能力,增强思维的灵活性、变通性和创新性。
如,进行《三角形的外角》教学时,结合知识特点,运用如下变式:
原型:如图1,∠BDC是________外角,∠BDC=______+_______,
∠EFC是________外角,∠EFC=______+_______,
∠EFC是_________外角,∠EFC=_______+______,∠EFC>_________.
说明:原型是三角形外角性质的基本应用。通过考察在图形的识别及应用性质,深化学生对于三角形的外角的理解。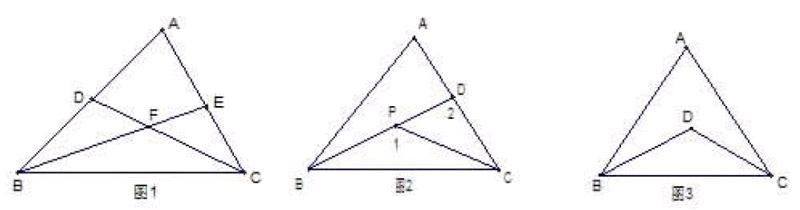
变式一 如图2,P是ΔABC内的一点,则∠A、∠1、∠2的大小关系为_______.
说明:在原型的基础上变化,两次使用外角性质,建立不等关系。
变式二 如图3,点D是ΔABC内的一点,连接BD和CD,证明∠BDC>∠A.
说明:在理解性质的基础上,灵活运用解决问题。在应用过程中,能根据需要选择合适的方法。通过一题多解,深化认知,开拓思路,发展数学思维。
变式三 如图4,∠A=50°,∠B=35°,∠C=25°,求∠BDC的度数。
说明:与变式二"形异而质同"。通过比较,学生在不同情境中运用知识,进一步加深对知识的理解,强化了应用能力,还得到了一个非常有用的结论:∠BDC=∠A+∠B+∠C。
变式四 如图5中,∠1+∠2+∠3+∠4=_______。
说明:可以证明,亦可直接利用变式三中的结论∠BDC=∠A+∠B+∠C。
变式五 如图6,CE是ΔABC的外角∠ACD的平分线,且CE交BA的延长线于E,证明∠BAC>∠B.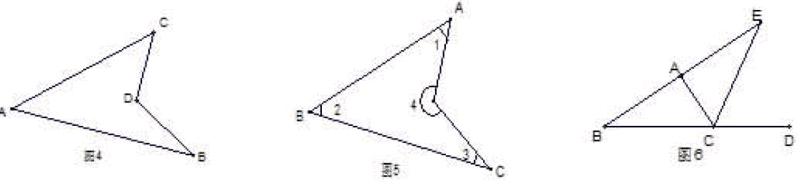
说明:本题难度较之前有提高,考察学生对性质的掌握情况和灵活运用。
小结:"变式教学"既是对教学内容的优化,也是对教学过程的优化。教学中,题组的选择很关键,要让各层次的学生都能够认真思考,积极参与,理解和掌握学习内容,形成自己的理解和认知。课堂中,知识的发生、发展是逐步深化的过程,灵活运用一题多解、多题一解,类比、联想等各种方式,可有效的激发学生的学习热情,培养学生的数学思维。
3.变式教学在实践中的应用
3.1在"概念教学"中采用变式,深化对概念的认识,掌握概念的本质。概念、定理、命题构成了数学大厦的支架。概念是客观事物本质属性在人脑中的反映,学习数学概念、定理,贵在掌握概念、定理的本质属性。设计适当的"概念性变式",可以帮助学生多角度理解问题:由直观到抽象,由具体到一般、排除背景干扰,凸现本质属性和明晰概念的外延。通过概念性变式教学,有利于学生真正理解概念的本质属性,进而建立新概念与已有概念的本质联系。
3.2利用变式教学,激发学生学习数学的兴趣和信心。变式教学的过程,就是一个让学生从易到难,逐步深化,循序渐进地认识问题、解决问题的过程。通过一系列变式引导,让学生在探索、实践、发现的过程中享受成功,在兴奋、愉快的情境中既学到了知识与方法,又培养了思维能力,让学生有信心去面对困难,自己去思考和解决。
从学生的生理心理特点来看,每个学生都有探索和创造的潜能,关键是如何激发他们学习的兴趣、动机和求知欲。巴普洛夫学说告诉我们:在学习活动中,若只有一种分析器连续使用,大脑皮层就容易产生抑制,使学生逐步失去注意,而运用多种分析器则可以提高大脑皮层的兴奋性,……,使注意得以较长时间的保持。运用变式教学能使学生对所学的内容与练习保持浓厚的兴趣,而且让学生体验到运用知识与技能解决问题的乐趣,从中促进智力和能力的提高。
3.3利用变式教学,把握问题本质,培养学生思维的广阔性和深刻性。"思维的广阔性"是指思维活动作用范围的广泛和全面的程度。它表现为思路开阔,能全面地分析问题多方面的思考问题,多角度的研究问题。"思维的深刻性"是指思维活动的抽象程度和逻辑水平。它表现为善于使用抽象概括,理解透彻深刻,推理严密,逻辑性强,并能解决难度较大的问题。数学教学中灵活运用变式的形式,根据数学概念、定理、命题的不同特征、差异和隐含关系等进行具体分析,设计不同的变式问题,一题多解、一法多用,对思维品质的提高有着积极的作用。
变式教学还可利用变式问题探究概念、定理、命题的实质及相互之间的联系,掌握其潜在的意义,而不被一些表面现象所迷惑。能使知识和方法得到迁移,培养学生思维的广阔性和深刻性。
4.变式教学实践中几个应注意的问题
4.1变式教学的阶段性和难度设置。根据学生的认知特点,在编制变式题组时,应注意循序渐进,题目应当有层次,既注意到知识产生、发展的脉络,同时,还要照顾到班级不同层次的学生。分为三个不同的阶段:一、初步练习阶段,指在开始接触变式训练时的适应阶段,主要是让学生掌握基本知识和基本方法;二、熟练掌握阶段,这是在学生已初步掌握基本技能的基础上组织的练习。可采用多种形式的变式题,精心挑选,合理安排,通过训练,使学生达到较高的技能技巧水平;三、灵活应用阶段,这是在学生已经熟练掌握一般练习的基础上进行。此时,可选择一些有一定难度的综合题、技巧题等,并要求学生开始尝试自拟变式题。
4.2变式教学应有明确的目的性。变式教学中,"变"的是形式,"不变"的是数学知识的本质,形式要为本质服务,要立足于教材。这就要求我们要根据不同的教学实际和需要,决定变式教学的形式和手段。教师要根据不同的教学实际和需要钻研教材,围绕教学目标创设适合变式教学的教学环境,这是变式教学的关键。只有明确了实际教学目的,我们才能明确哪些是知识内容的本质特征,哪些是非本质特征,从而明确了什么可以变,什么不可以变。
4.3变式教学的主体是学生,最终目的是培养学生的思维能力。创设变式题组时,要充分考虑到学生的特点,真正为学生解决疑难,使其获得发展。引入要适当,引申要合理,层次跳跃不要太大,让学生跳一跳就能够摘得到。要注意把握学生的思维脉络,在学生已有的认知基础上,使学生不至于感到生硬和突然,使思维平衡和谐地发展。实际教学中,每个学生因其知识结构、经验、学习能力等方面的差异,是有层次差别的。题组的设计要尽可能满足各个层次学生的需求,多让学生主动参与,自我尝试,主动反思问题的解决过程,只有这样,才能真正体现出变式教学的价值,起到培养学生思维能力的作用。
