一种基于DCT域局部能量的多聚焦图像融合算法

梁　聪　唐振华

(广西大学计算机与电子信息学院　广西 南宁 530004)



一种基于DCT域局部能量的多聚焦图像融合算法

梁聪唐振华*

(广西大学计算机与电子信息学院广西 南宁 530004)

摘要为了在无线视觉传感器网络等资源受限的应用中实现图像信息融合，提出一种基于离散余弦变换域DCT(Discrete Cosine Transform)中局部能量的多聚焦图像融合算法。该算法没有采用当前常用的基于对比度和方差的融合准则，而是通过计算图像在DCT域的局部能量，选择局部能量较大的分块实现融合。实验结果表明，该算法能获得良好的主观视觉融合效果，且在互信息、峰值信噪比和空间频率等客观指标上优于常用的基于小波变换的融合算法，计算量与基于DCT域方差的融合算法相比降低约41%～49%，该算法适用于诸如无线视觉传感器网络等资源受限或实时性要求高的应用场合。

关键词图像融合离散余弦变换局部能量视觉传感器网络

0引言

图像融合通过利用待融合图像之间信息的冗余性和互补性，将两幅或多幅图像合成为一幅比任一待融合图像包含更多信息的新图像。图像融合在医学成像、计算机视觉、遥感、气象预报和军事等领域有着广泛的应用前景。作为图像融合的应用之一，视觉传感器网络VSN(visual sensor networks)依靠地理分布不同节点上的视觉传感器来获取周围环境的图像/视频信息，以多跳中继的无线通信方式传输信息，在传感器节点上会涉及图像融合技术。

在VSN中，距离较近的相邻节点通常会获得相同场景下多幅图像信息，但由于这些图像由位置不同的节点获得，拍摄的聚焦点可能不同。对相同场景下的图像信息进行有效地融合，不仅降低网络传输图像信息的数据量，而且能够增强图像的重建质量。由于VSN中节点的能量有限和计算能力受限，应用于其中的图像融合算法除了获得优良的融合性能外，还应具有计算简单和处理速率快等特点，本文提出的算法满足要求。

在基于变换域的图像融合中，小波变换是常用和重要的方法[1-3]。但是基于这些变换的方法通常需要执行大量的复杂计算，耗费过多时间和内存资源，因此并不适用于资源受限的视觉传感器网络。在VSN中，传输图像数据之前通常会经过压缩和融合处理，以减少信息冗余度和降低电能消耗。离散余弦变换DCT作为一种多媒体压缩技术得到了广泛应用，直接在DCT域进行融合处理并不需要大量复杂的编解码操作，从而减少数据处理量与能量消耗，因此采用DCT域的融合算法更为高效。目前，在DCT域进行图像融合的研究并不多。文献[4]提出了一种DCT变换和提升小波变换相结合的融合算法，但是其计算复杂度过高。Tang等人[5]提出了一种利用局部对比度进行图像融合的方法，该方法选择对比度较大的DCT系数用于图像融合，但是计算对比度的过程比较复杂，而且融合图像出现了块效应和模糊现象。鉴于上述方法的不足，文献[6]提出了一种基于方差判断准则的方法，先将输入图像划分为DCT块，分别计算它们的方差，然后选择方差较大的块作为融合图像的DCT块。但是，该方法存在大量的平方运算，同样会耗费很多时间和计算资源，因此也不太适用于无线视觉传感器网络。

为了解决上述方法的不足，本文依据 DCT 变换的性质，提出一种基于局部能量进行图像融合的新算法。该算法选择局部能量较大的块作为融合图像的DCT块，由于运算很简单，因此更适用于资源受限的视觉传感器网络。本文通过主观和客观评价，对比了离散小波变换DWT(discrete wavelet transform)、SIDWT(shift invariant discrete wavelet transform)和基于方差的DCT方法，证明了本文提出的方法更加简单有效。

1基于局部能量的DCT域图像融合算法

1.1离散余弦变换

在离散余弦变换的系数中，从矩阵左上角到右下角依次对应着低频、中频和高频分量，高频系数通常小于低频系数，因而能量主要集中在低频分量。

设x(m, n)为数字图像矩阵，则N×N的DCT变换定义为：

(1)

N×N的IDCT变换定义为：

(2)

1.2算法描述

成像区域内不同深度的对象会引起摄像机不同程度的离焦，多聚焦图像中的模糊区域是由离焦造成的，离焦镜头系统在数学模型上可等效为一个低通系统，清晰图像经过低通滤波，在滤除高频分量和高频能量的同时，图像的总能量会有所损失，因此，总能量可作为判别清晰图像与模糊图像的准则。

本文融合算法的框图如图1所示。在本文算法中，首先将待融合的图像A和图像B分别进行分块DCT 变换，然后分别比较它们对应DCT 系数能量的大小，选择局部能量较大的块作为融合图像的DCT块，最后将融合的DCT块进行逆变换即可得到融合图像。实验发现，图像按像素分块的大小对处理速率与融合质量均有影响，分块较小时，由选择融合的图像块出现的误判会造成较多小面积的块效应，且处理速率较慢；分块较大时处理较快，出现误判的概率降低，但是因此造成的块效应面积会较大。兼顾融合效果和处理速率，本文算法DCT块取16×16。

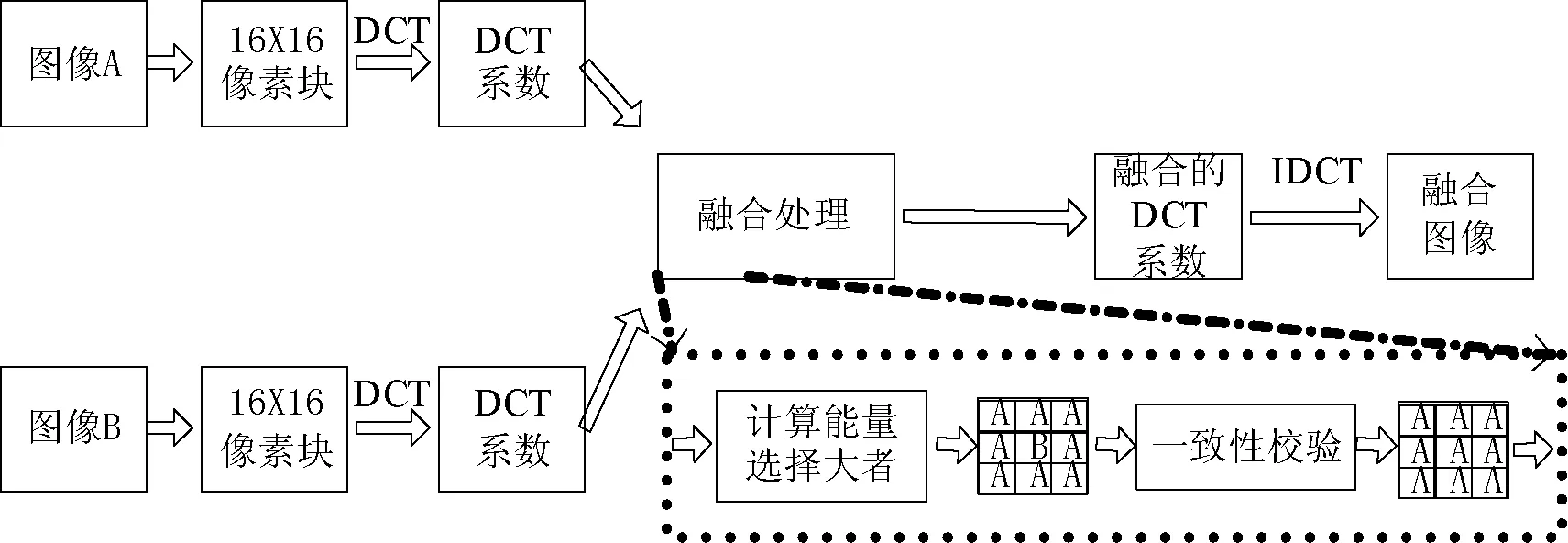
图1　本文融合算法框图

N×N系数矩阵的能量可定义为：

(3)

设x1(m,n)和x2(m,n)表示输入图像，x(m,n)为融合图像，在N×N块中选择能量大者为融合后x(m,n)的DCT块，即：

(4)

在比较能量大小时，可把比较图像A与图像B的d2(k,l)之和改为比较它们的|d(k,l)|之和，这样可避免平方运算，从而降低运算量和系统的能量消耗，即选择图像A和图像B的DCT块中绝对值之和较大者作为融合图像x(m,n)的DCT块，最后经过IDCT变换即可获得融合图像。本文中的融合规则按式(5)给出：

(5)

由于图像本身因素或者噪声的影响，在选择融合的DCT块时可能存在误判而产生块效应，因此有必要对融合后的图像进行一致性校验CV(consistency verification)。该处理过程是，在融合图像的分块区域中，如果处于中间的像素块来自输入图像B，而大多数周围的像素块来自输入图像A，那么可以认为来自输入图像B的像素块因误判而被错误地融合，经过一致性校验后它会被纠正为来自输入图像A相应的像素块。文献[6]使用了均值滤波器进行校验处理，但是由于在滤波器掩模内执行平均运算时可能出现平均“泛化”，因此有时并不能精确地纠正错误融合的像素块。针对此问题，本文使用的中值滤波器能够获得更好的校验效果。因为在融合图像的分块区域中，被错误融合的像素块只有少数一部分，多数像素块都是被正确地融合了，中值滤波器作为一种统计排序滤波器，可以有效地用多数的像素块取代少数的被错误融合的像素块。从后面的实验可以看出，应用中值滤波器进行一致性校验能有效地改善融合效果，实验使用的滤波器掩模大小为3×3。

2实验结果与分析

2.1评价标准

为了更全面地评价本文提出的算法，本实验引入两类客观标准来评价融合效果。第一类是需要原始图像的评价标准。互信息是两个变量之间相关性的度量，可衡量融合图像从输入图像中继承的信息量大小；峰值信噪比是一种基于图像信噪比的评价指标，值越大说明融合效果越好；另外本文引入了文献[7]中结构相似度的评价标准，该方法能够度量两幅图像结构上的失真。第二类评价标准不需要原始图像。由于在实际应用中一般不存在用作参考的理想图像，所以这类评价标准尤显重要。文献[8]提出了一种QAB/F的指标，它给出了融合图像从输入图像获得的边缘信息总量。文献[9]提出的Qw等指标，显示出有多少显著信息从输入图像转入了融合图像。此外本文实验还运用了一些比较常用的评价标准，平均梯度反映了图像中微小细节反差，值越大说明图像越清晰。空间频率反映图像在像素域的总体活跃程度。另外，运行时间可以反映算法的复杂度和耗费的计算资源。

2.2结果与分析

为了便于比较，本文选择目前公认融合效果较好的基于小波变换的融合算法DWT[1]和SIDWT[10]来进行比较，其中小波分解层为3，对应的融合小波系数选择最大原则。为了叙述方便，由式(5)确定的方法称为“本文方法”，而将经过中值滤波器进行一致性校验处理的方法称为“本文改进方法”。文献[6]提出的基于方差的方法记为“DCT+Variance”，进行均值滤波的一致性校验的方法记为“DCT+Variance+Cv”。为了与前面的评价标准相适应，用于实验的图像也有两类，图2带有原始图像，图3没有原始图像。表1和表3分别给出融合算法的各个评价指标，表2是运行时间。本实验仿真环境是Matlab 7.0。

图2　原始图像和融合图像

图3　原始图像和融合图像

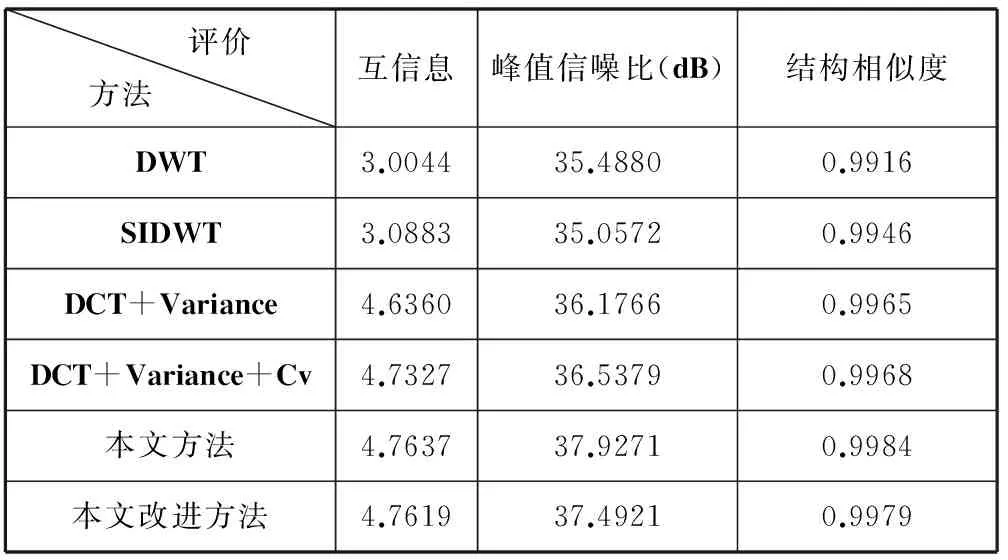
评价方法 互信息峰值信噪比(dB)结构相似度DWT3.004435.48800.9916SIDWT3.088335.05720.9946DCT+Variance4.636036.17660.9965DCT+Variance+Cv4.732736.53790.9968本文方法4.763737.92710.9984本文改进方法4.761937.49210.9979

表2　运行时间　　　　　　　(单位：秒)

从图2可看出，由本文提出的方法获得的(h)和(i)融合效果良好，和DWT、SIDWT方法获得融合图像在视觉效果上并无明显差异。由表1的评价数值看出，本文方法和本文改进方法优于基于小波变换的方法，同时也好于基于方差的方法。上述情况表明，本文提出的方法获得的融合图像能够从待融合图像中获取更多的原始的信息，融合质量更好。同时从表1还看出，是否经过一致性校验处理的融合图像在评价指标上相差不大，但是经过校验处理却能够获得更好的视觉融合效果。

表2给出了本文提出的方法和基于方差方法的运行时间。从表中数据可得出，本文的方法比基于方差方法节省了大约41%～49%的处理时间，尽管处理两个融合图像节省时间仅几秒，但是当整个传感器网络上成千上万个节点在处理数据时，本文提出的方法在降低时间消耗上将会非常可观。另外，本文的方法由于不需要复杂的平方运算，而只是低复杂度的求和运算，所以将会节省更多能量和计算资源，更适用于资源受限的视觉传感器网络。

图3是没有原始图像的情况下进行的对比，从图中可看出本文方法获得的(g)和(h)取得了更好的视觉效果，比如在图4局部放大图中，基于小波的(a)和(b)虽然整体上显得光滑，但是却造成了细微失真和对比度下降，这是因为小波变换在分解和重构图像的过程中会丢失信息；基于方差的(c)和(d)，可以看出存在一些块效应，原因是在这些融合区域错误地选择了输入图像块，同时说明了在亮度变化不明显的区域，基于方差的融合算法表现得不够健壮；本文方法(e)即使在没有经过一致性校验处理的情况下，也取得了良好的视觉效果。另外，加一致性校验模块的方法图(f)比不加模块的图(e)取得更好的视觉效果。表3给出了Qw、空间频率等评价指标，从中看出本文提出的方法和基于方差方法在评价数据上大体相当。

图4　局部放大图像

评价方法 QwQAB/F空间频率平均梯度DWT0.90870.62709.98413.5863SIDWT0.90450.68649.38383.4350

续表3

3结语

本文在离散余弦变换的基础上, 提出了一种基于局部能量的多聚焦图像融合算法，以及使用中值滤波器进行一致性校验的改进算法。该算法依据清晰图像具有较高能量的原理，在DCT域分别计算局部能量，然后选择局部能量较大的图像作为融合图像。实验中运用多种评价标准，将本文算法、基于小波变换以及基于方差的DCT算法进行了比较，结果表明本文算法获得的融合图像更清晰，计算复杂度更低，因此耗费时间和能量更少，特别适用于要求实时处理或资源受限的应用场合。

参考文献

[1] Li H,Manjunath B S,Mitra S K.Multisensor image fusion using the wavelet transform[J].Graphical Models and Image Processing,1995,57(3):235-245.

[2] Shreyamsha Kumar B K.Multifocus and multispectral image fusion based on pixel significance using discrete cosine harmonic wavelet transform[J].Signal,Image and Video Processing,2013,7(6):1125-1143.

[3] 高颖,王阿敏,王凤华,等.改进的小波变换算法在图像融合中的应用[J].激光技术,2013,20(5):690-695.

[4] 聂敏.一种改进的DCT变换图像融合技术[J].科技通报,2012,28(4):178-179.

[5] Tang J.A contrast based image fusion technique in the DCT domain[J].Digit Signal Process,2004,14(3):218-226.

[6] Haghighat M B A,Aghagolzadeh A,Seyedarabi H.Multi-focus image fusion for visual sensor networks in DCT domain[J].Computers and Electrical Engineering,2011,37(5):789-797.

[7] Wang Z,Bovik A C,Sheikh H R,et al.Image quality assessment: from error visibility to structural similarity[J].IEEE Trans Image Process,2004,13(4):600-612.

[8] Xydeas C S,Petrovic V.Objective image fusion performance measure[J].Electron Lett,2000,36(4):308-309.

[9] Piella G,Heijmans H.A new quality metric for image fusion[C]//Proceedings of international conference on image processing,2003,3:173-176.

[10] Rockinger O.Image sequence fusion using a shift-invariant wavelet transform[C]//Proceedings of IEEE international conference on image processing,1997,3:288-291.

A MULTI-FOCUS IMAGE FUSION ALGORITHM BASED ON LOCAL ENERGY IN DCT DOMAIN

Liang CongTang Zhenhua*

(SchoolofComputerandElectronicsInformation,GuangxiUniversity,Nanning530004,Guangxi,China)

AbstractIn order to apply image information fusion to resource-constrained applications such as wireless visual sensor networks, we presented a multi-focus image fusion algorithm, which is based on local energy in discrete cosine transform (DCT) domain. The proposed algorithm doesn’t employ commonly used rule of image fusion based on contrast and variance, but realises fusion by calculating the local energy of image in DCT domain and selecting the blocks with bigger local energy. Experimental results showed that the proposed algorithm could get good subjective visual effect of fusion, and outperformed those usual algorithms based on discrete wavelet transform in objective evaluation indexes such as mutual information, peak signal to noise ratio, space frequency and so on. Moreover, since the calculation decreases by around 41 percent to 49 percent in comparison with the fusion algorithm based on variance in DCT domain, the presented algorithm is suitable for the applications with resource-constrained or high real-time property like visual sensor networks.

KeywordsImage fusionDCTLocal energyVisual sensor networks

收稿日期：2014-12-04。国家自然科学基金项目(61461006，6126 1023)；广西自然科学基金项目(2013GXNSFBA019271)；广西教育厅科研项目(201106LX016)。梁聪，本科生，主研领域：多聚焦图像融合。唐振华，副教授。

中图分类号TP391

文献标识码A

DOI:10.3969/j.issn.1000-386x.2016.05.059