一种改进差分盒维法提取齿环分形特征的研究

赖科学， 陈　朗， 周伟松， 余　坤， 何　涛

(湖北工业大学现代制造质量工程重点实验室， 湖北 武汉 430068)

一种改进差分盒维法提取齿环分形特征的研究

赖科学， 陈朗， 周伟松， 余坤， 何涛

(湖北工业大学现代制造质量工程重点实验室， 湖北 武汉 430068)

[摘要]同步器齿环具有不规则和一定的统计自相似性的特征，可用分形方法中的分形维数对齿环图像进行描述，并将维数作为测量特征实现齿环缺陷识别。差分盒维法计算齿环图像维数时,结果会受到背景和摆放角度的影响，导致正常与缺耳齿环的维数结果存在交叉现象。针对这个问题，在研究和分析差分盒维数法的基础上提出一种改进差分盒维法，即利用概率和图像旋转消除图像背景和被测物摆放角度的影响，提高维数计算精度。通过改进差分盒维法对正常与缺耳齿环的分形维数计算与分析，可消除图像背景和摆放角度对维数产生的影响，实现了用齿环分形维数作为识别特征量对缺陷齿环的识别。

[关键词]同步器齿环； 改进差分盒维法； 分形维数； 缺陷识别

同步器齿环作为汽车变速箱中重要零件，缺齿、缺耳以及齿形不规则是困扰齿环制造质量的重要问题之一，直接影响汽车驾驶的灵巧性、舒适性和平稳可靠性[1-4]，因此，对齿环进行识别检测变得尤为重要。

分形理论被广泛运用到自然学科、工程技术、社会经济、文化艺术等诸多领域[5]。例如：Hua-Rong Peng等[6]用分形理论计算了建筑、钟楼、动物的分形维数(维数)；J.B.Florindo等[7]用分形理论计算了兔子、雨、手掌的维数；Dulan Amarasinghe等[8]用多种分形维数计算方法对放电图像进行维数计算。这些研究对象都不具有严格的自相似性，但存在一定的统计自相似性。

通过对齿环图像观察与分析，发现齿环图像具有不规则和一定的统计自相似性特征。因此，本文用分形理论方法获取同步器齿环缺耳的分形维数，并将其作为测量特征对齿环缺耳缺陷进行识别。计算分形维数的方法很多，差分盒维法由于计算方便被广泛应用。研究发现，传统差分盒维法可以估计齿环图像的分形维数，但是当齿环图像有大量背景且齿环在图像中随机旋转角度摆放时，差分盒维法计算出正常与缺耳齿环的分形维数存在交叉影响，不能够用分形维数作为测量特征对正常与缺耳齿环进行区分。为了解决这个问题，本文在差分盒维法的基础上提出一种改进差分盒维法，以解决齿环图像中存在背景及齿环在图像中随机角度摆放时分形维数不一致的问题。

1基于差分盒维法的分形维数分析

1.1差分盒维法

图 1　差分盒维法

nr(i,j)=l-k+1

(1)

其中：l表示最大像素值落入盒子序数，k表示最小像素值落入盒子序数。所以，在尺度r下测度

(2)

重复上述过程，得到一组不同尺度r下的测度Nr，并对log(1/r)和logNr这组数据进行最小二乘法拟合得到分形维数

(3)

1.2齿环图像分形维数计算

用差分盒维法计算齿环样本1、样本2(图2)分形维数时，将图像上的灰度值作为三维空间中z坐标，从而形成三维空间(图3)。根据式(2)计算样本1在不同尺度r下对应的Nr，对log(1/r)和logNr进行最小二乘法拟合，求得分形维数D=2.2280。同样的方法对样本2进行维数计算，得到分形维数D=2.3026。

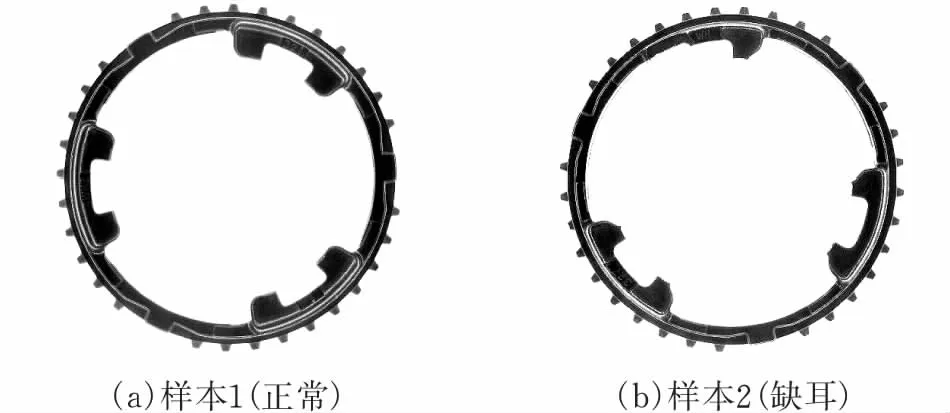
图 2　齿环样本原始图像

(a)样本1灰度三维图

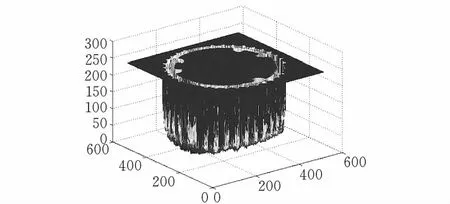
(b)样本2灰度三维图图 3　样本齿环灰度三维图

为了验证差分盒维法对同步器齿环缺陷识别的可靠性，用该方法对9组正常和缺耳齿环样本进行分形维数计算，结果如图4所示。正常组齿环平均维数分别为2.3027，维数波动范围为±0.0522；缺耳组齿环的平均维数为2.2991，维数波动范围为±0.0325。虽然正常组和缺耳组齿环的维数存在差别，但其维数的动态变化范围过大，使得维数存在交叉，所以，传统差分盒维法计算出齿环的维数结果不能用于区分正常和缺耳齿环。

图 4　差分盒维法计算9组齿环维数结果

1.3维数交叉的原因分析

从差分盒维法计算9组正常和缺耳齿环的维数结果可以看出两者之间的维数非常靠近，并且存在维数交叉的情况。该方法计算出维数结果不能区别正常和缺耳齿环的主要原因有以下两点：

1)由于齿环是环形结构且没有占满整个图像，在不同的角度下计算的Nr数值会不同，导致同一齿环在不同角度摆放下会产生不同的分形维数；

2)通过对齿环三维灰度图像(图3)分析，发现齿环图像中存在大量趋于255的背景值，影响了图像维数的计算精度，产生过度覆盖的问题，导致维数计算精度降低。

2改进差分盒维法

改进差分盒维法主要计算步骤为：

1)寻找图像背景的灰度值Gb。具体算法为：统计出每一行像素中出现次数最多的像素值，记为Gi(i为图像中像素的行数)，再统计出Gi中出现次数最多的像素值，记为Gb，并把Gb重新赋值为0。

2)对原始图像分别进行旋转90°、180°和270°(图5)，并用式(2)和式(3)计算不同角度下的测度Nr，可以得到0°、90°、180°和270°这4种角度下r对应的Nr,0、Nr,90、Nr,180和Nr,270数据，并对这四组数据取平均得到平均测度

(4)

(6)

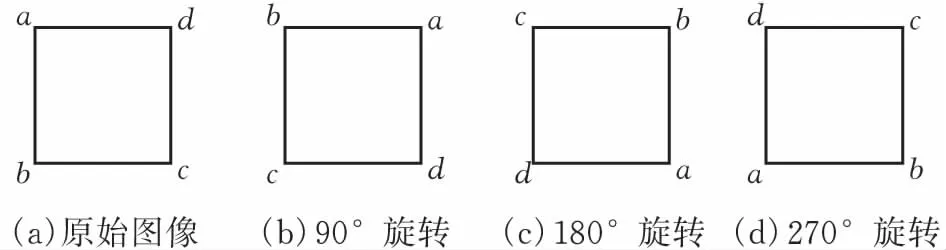
图 5　图像旋转

3改进法计算齿环分形维数及数据分析

通过对样本齿环三维图(图3)分析，发现图像背景中大量的灰度值都趋于255，对式(3)中盒子总数Nr存在干扰。针对这个问题，本文采用概率法找出齿环图像的背景灰度值Gb，并记其灰度值为0，结果如图6所示。

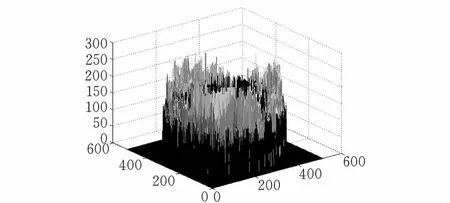
(a)样本1去背景灰度三维图

(b)样本2去背景灰度三维图图 6　去背景后样本齿环

为了进一步验证改进差分盒维法在实际应用中的可靠性，对9组正常和缺耳齿环样本进行维数计算，结果如图7所示，即：正常组齿环平均维数为2.2854，动态范围分别为±0.0033；缺耳组齿环的平均维数分别为2.2917，动态范围分别为±0.0055。改进差分盒维法计算的分形维数动态范围明显小于差分盒维法计算的动态范围，且改进差分盒维法能够实现对正常与缺耳齿环的识别。

表1　样本1、2在不同尺度r下对应的Nr

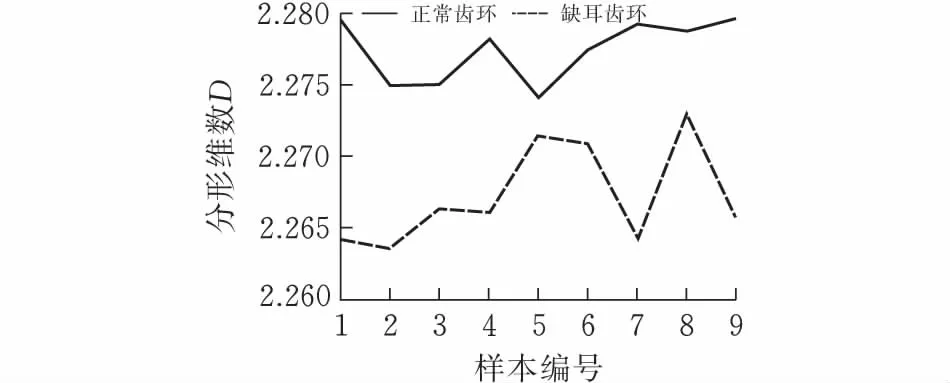
图 7　改进差分盒维法计算9组齿环维数结果

4结论

通过分形几何理论中差分盒维法的研究与分析，本文提出一种基于差分盒维法的改进差分盒维法。该方法通过概率方法和图像旋转的方法解决了图像背景和被测件随机摆放角度对维数的影响。通过用改进差分盒维法和差分盒维法对正常与缺耳齿环维数计算与分析，可得出以下结论：齿环具有一定的分形特征，分形理论可以对齿环维数测量特征进行分析。传统的差分盒维法计算同一图像在不同角度和存在背景的分形维数时会产生较大维数波动，不能精确计算其分形维数，导致传统差分盒维法不能够实现用维数特征对正常与缺耳齿环的识别。改进差分盒维法解决同一齿环在不同角度图像的分形维数不一致的问题，实现了齿环维数作为测量特征对正常和缺陷齿环的识别，并具有一定的稳定性。

[参考文献]

[1]李四年,陈园,叶甲旺,等. 汽车同步器齿环的生产现状与发展前景[J]. 湖北工业大学学报,2012(01):114-116.

[2]陈飞,温彤. 钢质齿环精锻成形工艺研究[J].模具技术,2006(06):39-41.

[3]Tseng C H, Yu C H. Advanced shifting control of synchronizer mechanisms for clutchless automatic manual transmission in an electric vehicle[J]. Mechanism and Machine Theory,2015, 84: 37-56.

[4]Hwanga B, Jeehoon Ahnb, Sunghak Lee. Effects of blending elements on wear resistance of plasma-sprayed molybdenum blend coatings used for automotive synchronizer rings[J]. Surface and Coatings Technology, 2005,194:256-264.

[5]Mandelbrot B B. The fractal geometry of nature[M].New York：Henry Holt and Company, 1983.

[6]Hua-Rong Peng,Lei Li, Qiong-Hua Wang. Property of robustness to size and its realization on fractal dimension[J]. Optik, 2014,125:2205-2209.

[7]Florindo J B， Backesb A R，deCastroc M，et al. A comparative study on multiscale fractal dimension descriptors[J]. Pattern Recognition Letters, 2012,33:798-806.

[8]Amarasinghe D, Sonnadara U， Berg M,et al.Fractal dimension of long electrical discharges[J].Journal of Electrostatics, 2015,73:33-37.

[9]王姮,卜燕,张华,等. 基于分形维数的磁痕图像缺陷检测[J]. 计算机应用研究,2015(02):603-605，612.

[责任编校： 张众]

Rotational on Extracting Fractal Feature of Gear Rings with an Improves Differnential Box-counting Method

LAI Kexue, CHEN Lang, ZHOU Weisong, YU Kun, HE Tao

(HubeiKeyLabofModernManufactureQualityEngin.,HubeiUniv.ofTech.,Wuhan430068,China)

Abstract：synchronizer rings (gear ring) present irregular shape and certain self-similar characteristics, so we can use fractal dimension to describe the gear ring images and achieve defect recognition as a measurement characteristics. When calculating the dimension of gear ring images with differential box-counting method, the results are effected by image background and display angle, leading to the cross phenomenon on dimensions of normal and missing ear gear rings. To solve this problem, this paper proposes a rotational differential box-counting method based on research and analysis of differential box-counting method. This method utilizes probabilistic and image rotation methods to eliminate the effects caused by image background and display angle, and improve the dimension accuracy. Fractal dimension of normal and missing ear gear rings are estimated by the rotational differential box-counting method. The results show that the effects of background and angle are eliminated and fractal dimension can be characterized as a measurement of normal and defective gear ring identification.

Keywords：synchronizer gear ring; rotational differential box-counting method; fractal dimension; defect detection

[收稿日期]2015-10-16

[基金项目]国家自然科学基金(51275158)

[作者简介]赖科学(1990-)， 男，四川隆昌人，湖北工业大学硕士研究生，研究方向为图像处理技术

[文章编号]1003-4684(2016)02-0005-04

[中图分类号]TP391.4

[文献标识码]：A