周期三对角Toeplitz矩阵的求逆算法及其稳定性

蔺小林, 蔺彦玲

(陕西科技大学 文理学院， 陕西 西安　710021)



周期三对角Toeplitz矩阵的求逆算法及其稳定性

蔺小林, 蔺彦玲

(陕西科技大学 文理学院， 陕西 西安710021)

摘要：提出了一种求解周期三对角Toeplitz矩阵逆的新算法，其思想为通过周期三对角Toeplitz矩阵的特殊结构，利用矩阵的LU分解，以及矩阵方程的求解方法，先求出逆矩阵的第一列和最后一列，然后依次求出逆矩阵的其他列.该算法不需要对矩阵的各阶顺序主子式进行限制，同时适用于计算机实现的代数系统.算法稳定性较好并且算法复杂性较低，最后通过数值例子验证了算法的有效性和较强的稳定性.

关键词：周期三对角Toeplitz矩阵; LU分解; 逆矩阵; 稳定性

0引言

在现代数据处理中，往往要求解决一些对角线性方程问题，包括三对角、五对角、七对角，以及三对角Toeplitz、五对角Toeplitz等线性方程问题.早期，便有学者研究了三对角、五对角及七对角线性方程问题，并给出了各种求解对角矩阵的逆矩阵的方法，在文献[1-11]中给出了三对角和五对角矩阵以及其周期对角矩阵和块对角矩阵的逆矩阵，在文献[12-14]中给出了七对角矩阵和广义七对角矩阵的逆，而其中利用LU分解和Doolittle分解进行求解逆矩阵的见文献[3-5,7,9,10,12-14]. 同时，三对角Toeplitz、五对角Toeplitz线性方程问题也在不断研究中，见文献[15-17]. 其中文献[15]先将Toeplitz矩阵扩展为循环矩阵，通过求出循环矩阵的逆以及对循环矩阵的分块求出原Toeplitz矩阵的逆，同时讨论了算法的稳定性.文献[16]给出了对角Toeplitz矩阵逆元素的解析计算表达式.

在以上文献的启发下，本文给出一个求解周期三对角Toeplitz矩阵的逆矩阵的快速稳定算法，该算法适用于多种计算机代数系统，如：Mathematics,Macsyma,Matlab和Mapla等.并且该算法具有较低的复杂度和好的稳定性.

本文其他部分组成结构为：在第1节中，给出求解周期三对角Toeplitz矩阵的逆的求解方法，并讨论了新算法的复杂度；在第2节中，通过2个数值例子验证了算法的有效性，并证明了该算法的稳定性；最后，进行小结.

1主要结论

周期三对角Teoplitz矩阵如下

(1)

其中abc≠0.

定理若n×n阶广义周期三对角矩阵T的顺序主子式Dk≠0，k=1,2,…,n，则T有唯一的LU分解.

T=LU

其中

(2)

(3)

从而，有

(4)

该定理详细证明过程略，可参阅文献[17，18]相关内容.

由T=LU可得以下方程

αi=a, i=1a-βi-1γi, i=2,3,…,n-1a-∑n-1i=1μivi i=nìîíïïïï

(5)

βi=b,i=1,2,…,n-2

(6)

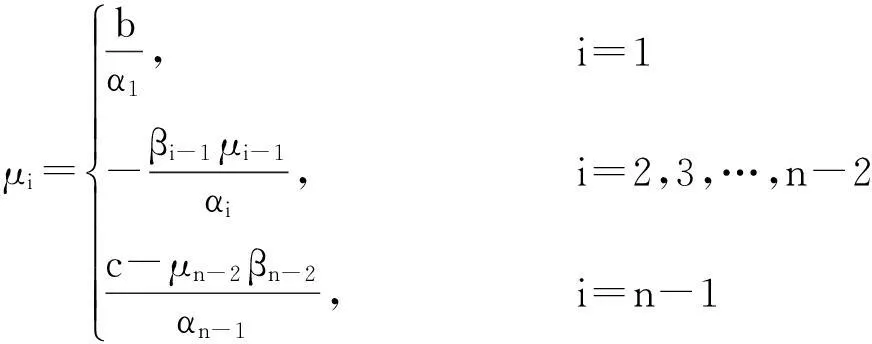
(7)

(8)

(9)

假设矩阵T非奇异且其逆矩阵为

T-1=(S1,S2,…,Sn)

其中Sj表示T-1的第j列，j=1,2,…,n.这里Sj可以写成

Sj=(S1,S2,…,Sn)Ej

其中Ej=(δ1j,δ2j,…,δnj)t,j=1,2,…,n,且δij为Kronecker 符号.

通过T-1T=In(这里的In是n×n单位矩阵)，可以得到以下关系

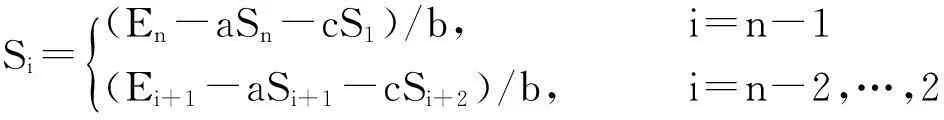
Si=(En-aSn-cS1)/b, i=n-1(Ei+1-aSi+1-cSi+2)/b, i=n-2,…,2{

(10)

由(10)式可以看出，只要求出Sn和S1，便可迭代求出Sn-1,Sn-2,…,S2，以下进行求解Sn和S1.

由于

TT-1=T(S1,S2,…,Sn)=(E1,E2,…,En),

从而由第一个和最后一个方程可得TS1=E1和TSn=En，即L(US1)=E1和L(USn)=En，那么可得出以下四个方程

LY=E1

(11)

US1=Y

(12)

LX=En

(13)

USn=X

(14)

其中Y=(y1,y2,…,yn)t，S1=(s11,s21,…,sn1)t，

X=(x1,x2,…,xn)t，Sn=(s1n,s2n,…,snn)t.

由式(11)得

yi=1, i=1-γiyi-1, i=2,3,…,n-1-∑n-1i=1μiyi i=nìîíïïïï

(15)

由式(12)和(15)可得

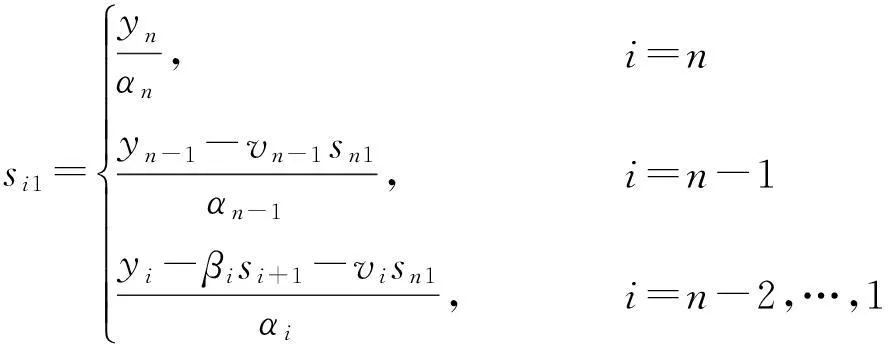
si1=ynαn, i=nyn-1-vn-1sn1αn-1, i=n-1yi-βisi+1-visn1αi, i=n-2,…,1ìîíïïïïïïïï

(16)

同样，根据式(13)和(14)可得

X=(0,0,…,0,1)t

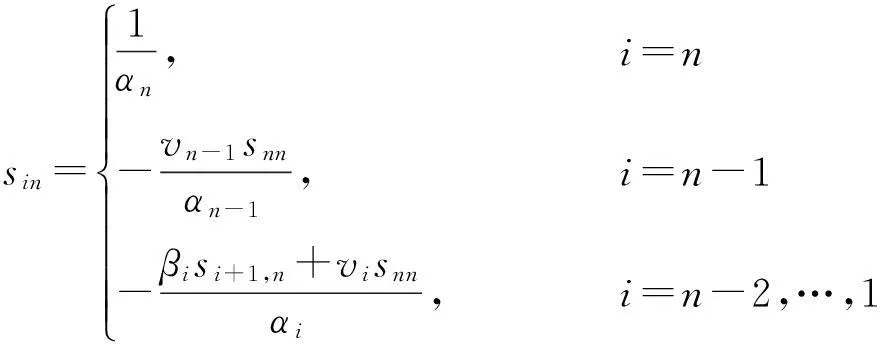
(17)

(18)

因此，将Sn和S1带入式(10)，便可迭代得到T-1的其他列向量Sn-1,Sn-2,…,S2，如此便得出周期三对角Toeplitz矩阵T的逆矩阵.

矩阵T求逆算法

输入：矩阵的阶n，矩阵元素a,b,c；

输出：逆矩阵T-1；

步骤1：当i=1,2,…,n-2时，令βi=b；

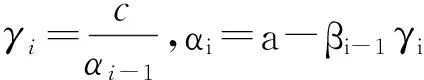
步骤3：令v1=c，当i=2,3,…,n-2时，计算vi=-viγi，并令vn-1=b-vn-2γn-1；

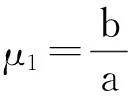
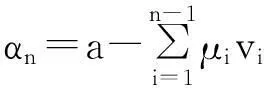
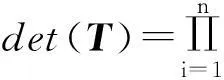
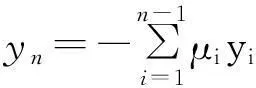
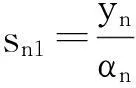
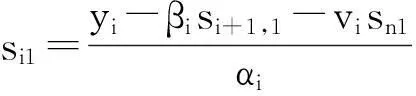
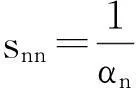
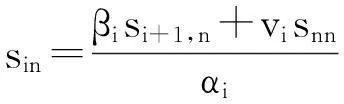
步骤10：将Sn和S1带入式(10)，依次求出Sn-1,Sn-2,…,S2.

算法复杂度

步骤1和步骤10的算法复杂度均为n-2阶，步骤2的算法复杂度为2n-3阶，步骤3至步骤5的算法复杂度均为n-1阶，步骤6至步骤9的算法复杂度均为n阶.综上所述，该算法的算法复杂度为11n-10阶，因此该算法的复杂度仅仅与矩阵的大小n有关，而文献[15]中求三对角与五对角Toeplitz矩阵求逆的算法中的算法2的复杂度为O(nlog2n)阶.

2数值例子

例1考虑6×6周期三对角Toeplitz矩阵

的逆矩阵.

通过矩阵T求逆算法可得

β=(2,2,2,2)

(步骤1)

γ=(0,3,-0.6,1.3637,-1.7368)

(步骤2)

v=(3,-9,-5.4,7.3636,14.7895)

(步骤3)

μ=(2,0.8,-0.7273,-0.8421,1.0471)

(步骤4)

α=(1,-5,2.2,1.7273,4.4737,-11.0118)

(步骤 2,5)

det(T)=-936

(步骤6)

y=(1,-3,-1.8,2.4545,4.2632,-3.3059)

(步骤7)

S1=(-0.09081196581197,0.09508547008547,0.08867521367521,-0.18696581196581,-0.03952991452991,0.30021367521368)

(步骤8)

Sn=(0.09508547008547,0.08867521367521,

-0.18696581196581,-0.03952991452991,

0.300213675368,-0.09081196581197)

(步骤9)

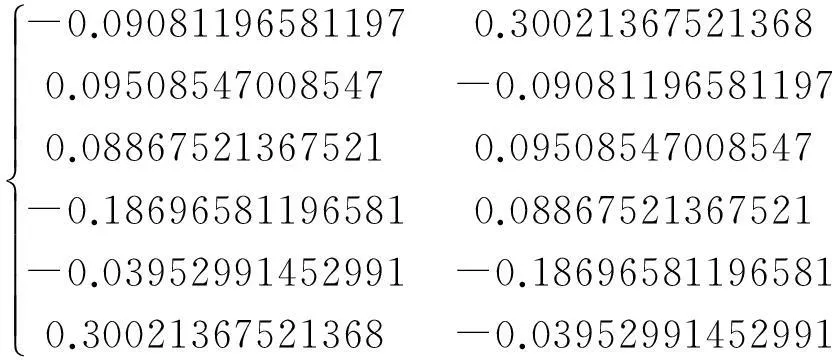
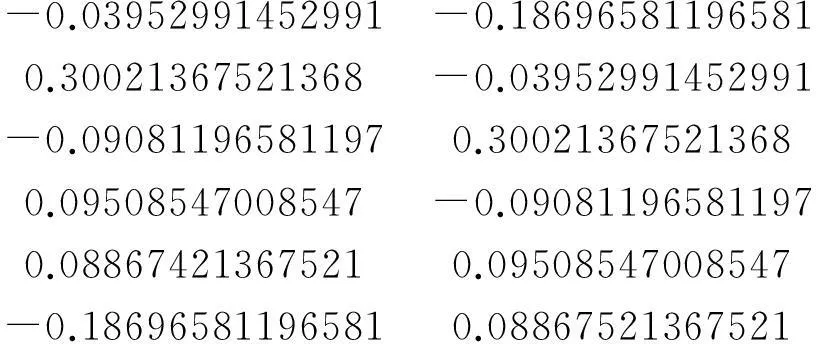
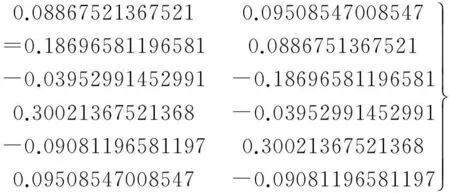
因此，由步骤10可得

T-1=

例2考虑n×n阶的周期三对角Toeplitz矩阵

表1　求周期三对角Toeplitz矩阵各阶

例2的数据表明，对于正常态周期三对角Toeplitz矩阵的逆，矩阵T求逆算法是稳定的.

3结论

本文主要给出了一个求解周期三对角Toeplitz矩阵的快速稳定的新算法，该算法既结合了求解对角矩阵的逆矩阵的LU分解方法，又结合了求解Toeplitz矩阵的逆矩阵的思想，不仅求解出了周期三对角Toeplitz矩阵的逆，同时也保证了算法的高度稳定性.为该类问题的求解提供了新的方法.

参考文献

[1] Ahmed Driss Aiat Hadj,Mohamed Elouafi.A fast numerical algorithm for the inverse of a tridiagonal and pentadiagonal matrix[J].Applied Mathematics and Computation,2008,202:441-445.

[2] M.E.Kanal,N.A.Baykara,M.Demiralp.Theory and algorithm of the inversion method for pentadiagonal matrices[J].J Math Chem,2012,20:289-299.

[3] Emrah Kihc.Explicit formula for the inverse of a tridiagonal matrix by backward continued fractions[J].Applied Mathematics and Computation,2008，197:345-357.

[4] Moawwad El Mikkawy,El Desouky Rahmo.A new recursive algorithm for inverting general periodic pentadiagonal and anti-pentadiagonal matrices[J].Applied Mathematics and Computation,2009,207:164-170.

[5] A.A.Karawia.A computational algorithm for solving periodic penta-diagonal linear systems[J].Applied Mathematics and Computation,2006,174:613-618.

[6] 余承依,陈跃辉.周期三对角矩阵逆的一种新算法[J].数学的实践与认识,2010,40(22):192-198.

[7] 冉瑞生,黄廷祝,刘兴平，等.三对角矩阵求逆的算法[J].应用数学和力学,2009,30(2):238-244.

[8] 唐达.周期三对角矩阵求逆的快速算法[J].上海电机学院学报,2013,16(5):300-304.

[9] Moawwad EI Mikkawy,EI Desouky Rahmo.Symbolic algorithm for inverting cyclic pentadiagonal matrices recursively-derivation and implementation[J].Computer and Mathematics with Applications,2010,59:1 386-1 396.

[10] 冉瑞生,黄廷祝.块三对角矩阵的逆[J].电子科技大学学报,2007,36(2):341-342.

[11] 陈芳,陆全,袁志杰.分块五对角矩阵求逆的快速算法[J].合肥工业大学学报,2008,31(11):1 904-1 907.

[12] Lin Xiao-lin,Huo Pei-pei,Jia Ji-teng.A new recursive algorithm for inverting general periodic sevendiagonal and anti-sevendiagonal matrices[J].Far East Journal of Applied Mathematics,2014,86(1):41-55.

[13] 贾纪腾,蔺小林.广义周期七对角矩阵求逆的新算法[J].纯粹数学与应用数学,2010,26(6):1 040-1 046.

[14]A.A.Karawia.Inversionofgeneralcyclicheptadiagonalmatrices[J].MathematicsProblemsinEngineering,2013(2013):1-9.

[15] 刘刚,黄廷祝.三对角与五对角Toeplitz矩阵求逆的算法[J].纯粹数学与应用数学,2010,26(2):292-299.

[16] 宋以胜，张传定，张书华.三对角、五对角对称Toeplitz矩阵的解析逆阵[J].测绘学院学报，2004,21(2):82-84.

[17]DieleF,LopezL.Theuseofthefactorizationoffive-diagonalmatricesbytridiagonalToeplitzmatrices[J].Appl.Math.Lett.,1998,11:61-69.

[18]RaoS.Appliednumericalmethodsforengineersandscientists[M].Prentice-Hall:UpperSaddleRiver,2002.

【责任编辑：蒋亚儒】

An algorithm for computing the inverse of a periodic tridiagonal toeplitz matrix and the steadiness

LIN Xiao-lin, LIN Yan-ling

(College of Arts and Sciences， Shaanxi University of Science & Technology, Xi′an 710021, China)

Abstract:In this article, we presents a new algorithm for solving a periodic tridiagonal Toeplitz matrix inversion, which is thought by the special structure of a periodic Toeplitz tridiagonal matrix and using the LU factorization,as well as a method for solving the matrix equations.We get the first column and the last column of the inverse matrix firstly,then obtain the others.By using this method, the condition that each principal minor sequence of the matrix must nonzero is unnecessary.What′s more,the algorithm is suited for implementation using computer algebra systems with better algorithm steadiness and low algorithmic complexity.Finally, illustrative examples are given to demonstrates the effectiveness and steadiness of the algorithm.

Key words:a periodic tridiagonal Toeplitz matrix; LU factorization; inverse matrix; steadiness

中图分类号：O151.21

文献标志码：A

文章编号：1000-5811(2016)03-0171-04

作者简介:蔺小林(1961-)，男，陕西洛川人，教授，博士，研究方向：数值计算理论及其应用

基金项目：陕西省科技厅重点实验室科研计划项目(2011HBSZS014)； 陕西科技大学学术团队计划项目(2013XSD39)

收稿日期:2016-03-30