基于时变地震损伤模型的多龄期钢框架结构易损性分析①

王晓飞, 王鹏飞, 贾　虎, 郑伟花, 田　进

(1.南阳师范学院土木建筑工程学院,河南 南阳 473061;2.青岛市公用建筑设计研究院有限公司,山东 青岛 710055)



基于时变地震损伤模型的多龄期钢框架结构易损性分析①

王晓飞1, 王鹏飞1, 贾虎1, 郑伟花1, 田进2

(1.南阳师范学院土木建筑工程学院,河南 南阳 473061;2.青岛市公用建筑设计研究院有限公司,山东 青岛 710055)

摘要：基于时变地震损伤模型提出酸性大气环境作用下多龄期钢框架结构概率地震易损性分析的方法及步骤;考虑服役龄期对钢框架结构抗震性能的影响,分别建立时变概率地震需求模型、时变概率抗震能力模型及时变易损性模型;在概率地震需求分析及概率抗震能力分析的基础上,得到多龄期(20年、30年、40年、50年)钢框架结构的易损性模型及易损性曲线。

关键词：多龄期; 钢框架结构; 时变地震损伤模型; 易损性

0概述

地震易损性分析可以预测结构在不同等级的地震作用下发生各级破坏的概率,对于结构的抗震设计、加固和维修决策具有重要的应用价值[1]。地震易损性研究方法主要包括经验易损性分析方法、试验易损性分析方法、解析易损性分析方法或其中两者的组合方法。在某些地震灾害数据较多的地方,经验易损性是最精确的研究方法,但并不是所有地区都会发生足够多的地震,能让研究人员获得足够多评价结构发生各级破坏概率的数据。试验易损性分析方法是建立在试验研究的基础上,得到的结构破坏评价指标比较可信,但开展试验研究的代价较大。相比较以上两种方法,解析易损性分析方法的最大优点便是快速、经济。

目前,从国内外研究成果[2]中可以归纳出影响建筑结构地震易损性的主要因素有:结构类型、建筑年代(包括建筑设计所依据的规范及建筑服役龄期)、设防烈度、场地类别、层数等。针对各种结构地震易损性的研究已经相当成熟,而考虑服役龄期对建筑结构地震易损性的影响并建立多龄期建筑结构易损性曲线,在目前的地震易损性研究领域尚属空白。鉴于此,本文在郑山锁等[3]提出的时变地震损伤模型的基础上提出了多龄期钢框架结构地震易损性分析方法及步骤,并得到多龄期(20年、30年、40年及50年)钢框架结构的易损性模型及易损性曲线。

1锈蚀钢材损伤退化规律

1.1钢材的起锈时间与锈蚀速率

导致钢结构防腐涂层失效和决定锈蚀速率大小的原因主要有:环境因素、涂层厚度、结构形式及金属表面除锈质量等级等。虽然影响防腐涂层失效的原因很明确,但其失效机理却很复杂,且目前环境变化迅速,很难准确预测涂层的失效起始时间(即钢材的起锈时间)及锈蚀速率。

对多龄期钢框架结构进行易损性分析,需要具体确定钢材的起锈时间和锈蚀速率。因此本文尝试在相关规范及文献数据的基础上,初步估计一个基本符合实际情况的钢材起锈时间及腐蚀速率。

钢结构建筑在建造初期会做防腐处理,防腐涂层保护时间的长短与外部环境类型、防腐涂层的类型与厚度有关。根据《工业建筑防腐蚀设计规范》[4]的规定,钢结构的表面防护应符合表1的规定。

由表1及相关文献[5]确定钢结构防护层的平均使用年限为20年。

根据《金属腐蚀电化学热力学》[6]可以得到碳钢在各类大气中的腐蚀速率,如表2所列。

表2　碳钢在各类大气中的腐蚀速率

由表2及相关文献[7-8],本文认为Q235碳钢在一般城市酸性大气环境中的平均腐蚀速率为0.02 mm/a。

1.2失重率Dw与平均腐蚀速率y之间的关系

为了衡量钢材的锈蚀程度,引入失重率Dw来描述钢材的锈蚀程度。失重率Dw越大则该钢材的锈蚀程度越大,其数学表达式为:

Dw=(W0-W1)/W0

(1)

式中:W0、W1分别为腐蚀前与腐蚀后钢材试件的质量。

(2)

设钢材在酸性大气环境下的平均腐蚀速率为y,单位为mm/a,而钢材的起锈时间确定为服役20年。为方便计算,认为同一框架结构上的框架柱、梁构件均匀锈蚀,那么对于服役t年的钢结构来说,其钢材的平均锈蚀厚度为yt=y·(t-15),对于工字型截面型钢(图1、2),锈蚀构件截面高度hη=b-2yt,宽度bη=b-2yt,则设计截面面积A0的构件在酸性大气环境作用下一定服役龄期t时截面腐蚀面积At可以表示成:

A0=2bta+htw-2twta

(3)

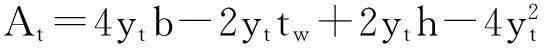
(4)

将式(3)、(4)代入式(2),可得到锈蚀率η与平均锈蚀深度yt之间的关系:

(5)

图1　无锈蚀型钢截面Fig.1　Steel section with no corrosion

图2　锈蚀深度为yt的型钢截面Fig.2　The steel section with corrosion depth of yt

1.3锈蚀对钢材力学性能的影响

环境作用下钢结构锈蚀会引起钢构件截面面积减小、钢材力学性能退化,进而引起钢构件乃至钢结构抗震性能的退化。史炜洲等[9]基于腐蚀钢材力学性能试验,运用最小二乘法线性法对试验结果进行回归,得到受腐蚀Q235B钢材屈服强度和极限强度与其锈蚀率之间的关系:

fy,η/fy=1-0.985 2η

(6)

fu,η/fu=1-0.973 2η

(7)

其中:fy、fy,η分别为钢材锈蚀前后的屈服强度;fu、fu,η分别为钢材锈蚀前后的极限强度。

对于腐蚀前的钢材,弹性模量E取2.06×105MPa;对于锈蚀后的钢材,参照LeeHS等[10]提出的钢筋的弹性模量随锈蚀率下降的公式进行取值。

Eη/E=1-0.75η

(8)

式中:E、Eη分别为钢材锈蚀前后的弹性模量。

将式(5)代入式(6)、(7)、(8),即可获得锈蚀钢材力学性能与钢材平均锈蚀深度yt的关系。

2多龄期钢框架结构地震易损性分析方法步骤

以多龄期钢框架结构整体损伤指数为指标的地震易损性分析方法的基本步骤如下:

(1) 建立正确合理的结构数值分析模型;

(2) 统计分析结构的地震需求参数(损伤指标)与地震动强度之间的关系,即建立结构的概率地震损伤需求模型;

(3) 考虑地震动的随机性,选择足够数量满足条件的地震动记录,进行IDA分析,即对结构进行概率抗震能力分析;

(4) 定义合理的结构损伤破坏状态及相应的损伤破坏极限状态;

(5) 建立结构易损性模型,绘制易损性曲线。

3在役钢框架结构的概率时变地震损伤需求分析

概率地震需求分析主要研究地震动强度与结构反应之间的相互关系,最终建立概率地震损伤需求模型。利用文献[3]中时变地震损伤指标的研究结果,将结构的地震需求参数取为不同的地震损伤指标,对多龄期钢框架结构进行概率地震损伤需求分析,并建立各自的对数线性化地震损伤需求模型。

郑山锁等[3]所建立的锈蚀钢结构地震损伤模型为:

(9)

式(9)中相关参数的确定详见文献[3]。

3.1时变概率地震损伤需求模型

本文的概率地震损伤需求模型中的结构地震需求参数采用的是损伤指标,地震动强度参数采用的是峰值加速度PGA。

文献[11]指出地震需求D的中位值mD和地震动IM之间一般服从幂指数回归关系,且结构的地震需求D与地震能力C均服从对数正态分布:

mD=a(IM)b

(10)

在考虑结构服役时间t对地震易损性的影响时,式(10)的拟合参数a、b及概率地震需求分析的对数标准差βD将变为时间t的函数。因此式(10)可写为:

mD(t)=a(t)(IM)b(t)

(11)

式中:a(t)、b(t)均是考虑服役时间因素的地震需求mD的拟合参数。

将式(11)进行对数变换,可得对数线性化时变概率地震损伤需求模型为:

ln[mD(t)]=ln[a(t)]+b(t)ln(IM)

(12)

令c(t)=ln[a(t)],则式(12)转换为:

ln[mD(t)]=c(t)+b(t)ln(IM)

(13)

结构反应的概率函数D用对数正态分布函数表示,其统计参数的计算如下:

(14)

(15)

3.2概率地震损伤需求分析方法

对结构进行概率地震需求分析最常用的方法是增量动力分析方法(IDA)及云图法[12]。

IDA方法或云图法都是通过对确定性的结构进行一系列地震动作用下的非线性动力反应分析,以考虑地震动“记录对记录(Record-to-Record,RTR)”的不确定性[12],但这两种方法都不能考虑结构自身的不确定性。为了能够同时考虑地震动与结构自身的不确定性,本文采用蒙特卡洛随机模拟方法(Monte Carlo法)与IDA方法相结合的方式对多龄期钢框架结构进行地震损伤需求分析,其分析步骤为:

(1) 按照地震波选取原则[13],选择足够数量的地震波并对其预处理;

(2) 利用Monte Carlo法随机抽样产生不同服役时间的结构随机样本,每一服役时间的结构随机样本数要与地震波数量相同,再将地震波与结构样本随机搭配,生成相同数量的地震波—结构样本;

(3) 对每一个地震波—结构样本进行IDA分析;

(4) 统计每一服役时间结构反应的样本均值。

上述Monte Carlo法与IDA方法相结合的地震损伤需求分析方法的详细流程如图3所示。

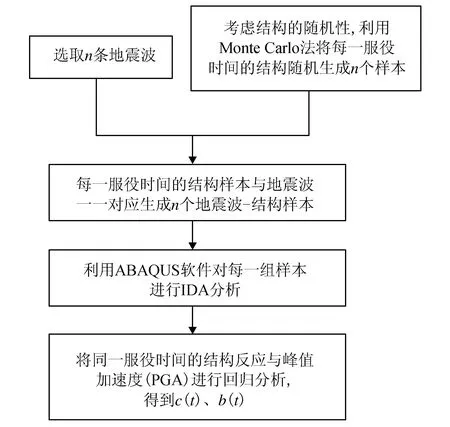
图3　　　Monte Carlo法与IDA方法相结合的　　　地震损伤需求分析流程图Fig.3　　　Flow chart of seismic damage demand analysis by　　　using Monte Carlo method and IDA method

3.3地震波的选取

本文对结构进行增量动力分析(IDA)分析时,根据美国ATC-63(2008)报告[13]的选波原则进行地震波的选择,在美国太平洋地震研究中心(PEER)的强震数据库中,选取20条地震动记录作为输入。所选地震波如表3所列。

表3　地震动记录

对结构进行IDA分析时,需要对上述地震波进行调幅。IDA方法中调幅的原则一般分为等步调幅和不等步调幅。考虑到钢框架结构在多遇地震作用下基本上处于弹性状态,而在罕遇地震作用下处于弹塑性状态,所以本文采用不等步调幅,每个算例结构分析时地震动记录最大加速度峰值依次取为0.07g、0.215g、0.4g、0.62g、0.8g、0.9g和1.0g。

3.4结构不确定性及随机样本的生成

本文主要考虑材料特性随机性,未锈蚀钢框架结构参数的统计特征见表4。利用式(6)、(8)计算锈蚀钢框架结构的钢材屈服强度和弹性模量的标准值,所有锈蚀钢框架结构的钢材屈服后刚度比标准值都取0.02。假设锈蚀钢框架的钢材屈服强度、弹性模量、屈服后刚度比的变异系数及分布类型与未锈蚀结构的完全相同。

表4　算例结构参数的统计特征

根据蒙特卡洛(Monte Carlo)随机抽样,若随机变量服从正态分布,则由式(16)产生随机样本[14]:

(16)

式中:x为服从正态分布的随机变量;μ、σ分别为随机变量的均值和标准差;Ri为[0,1]的伪随机数。对数正态分布的随机变量可通过与正态分布变量的对应关系产生,由式(17)得到服从对数正态分布的样本y:

y=exp(x)

(17)

不同服役时间的结构随机样本可表示成:

(18)

式中:μ(t)为服役时间t时的随机变量均值;δ为随机变量的变异系数;x,Ri的含义同式(16)。

3.5算例的概率时变地震损伤需求分析

3.5.1算例

算例采用文献[3]中的结构算例。框架结构各参数详见文献[3],限于篇幅,文中不再详述。

利用3.2、3.3、3.4节方法在MATLAB软件中生成服役龄期为20年、30年、40年及50年的5层两跨钢框架结构-地震波样本。

3.5.2地震需求分析

对不同龄期(20年、30年、40年、50年)的结构-地震波样本进行IDA分析,所得分析结果见图4。

图4　不同龄期结构整体损伤回归分析Fig.4　Regression analysis of global damage of structures with different ages

不同服役龄期的钢框架结构概率地震损伤需求模型为:

(19)

各式拟合精度分别为0.865、0.913、0.915、0.877。

基于上述IDA分析结果及式(15)可得到不同龄期结构地震需求的对数标准差(表5)。

表5　不同龄期结构地震需求的对数标准差

4在役钢框架结构的概率抗震能力分析

4.1时变概率抗震能力模型

结构的概率抗震能力模型表征的是在给定地震需求水平下,结构发生或超过不同破坏等级的条件概率。在地震易损性分析中,结构能力C通常假设服从对数正态分布,也可称之为概率抗震能力模型(Probabilistic Seismic Capacity Model,PSCM),如下所示[15]:

Fc(mD)=P[D>C|D=mD]=

(20)

同样考虑服役龄期t对钢框架结构抗震性能的影响,式(20)可以变为t的函数,即时变概率抗震能力模型:

Fc[mD(t)]=P[D>C|D=mD(t)]=

(21)

式中:mC(t)和βC(t)分别为服役龄期为t的结构极限状态抗震能力的中位值和对数标准差。

4.2破坏状态的划分与极限状态的定义

文献[3]确定钢框架结构的5个破坏状态及对应这5种破坏状态的损伤指标范围,详见表6。

表6　钢框架结构的损伤指标范围

极限状态为结构的性能水准,相邻破坏状态的临界点即为极限状态。针对以上五个破坏状态可定义4个极限状态:LS1、LS2、LS3、LS4,并在表6的基础上定义极限状态损伤限值(图5)。

图5　钢框架结构破坏状态划分与极限状态定义Fig.5　　　Damage state division and limit state definition　　　of steel frame structure

损伤指标界定的依据不考虑锈蚀影响,由图5可以确定式(21)中的mC(t),4个极限状态钢框架结构抗震能力的中位值分别为0.2、0.4、0.6、0.9。

根据文献[16]确定对数标准差βC(t)为0.25。

5在役钢框架结构的概率地震易损性分析

结构的易损性曲线表示在不同强度地震作用下结构反应D超过破坏阶段所定义的结构承载能力C的条件概率。因为结构地震反应D和结构能力C都服从对数正态分布,所以特定阶段的失效概率可由式(22)确定[17]:

Pf(PGA)=P[D(t)≥C(t)]=

(22)

式中:mD(t)为结构地震反应D的均值,由式(19)表示;标准差βD由表(4)确定;mC(t)为结构能力均值,以结构的损伤为指标,见图5;βC(t)为0.25。

将式(19)及表5各数值代入失效概率式(22),得到结构在不同极限状态、不同地震动强度PGA作用下的失效概率,见式(23),并绘制成易损性曲线(图6)。

(23)

图6给出了不同龄期钢框架结构的地震易损性曲线。将图6中某一特定极限状态下不同龄期钢框架结构的地震易损性曲线绘制在同一张图上,得到图7。由图7可以直观地看出,随着结构服役龄期的增大,钢框架结构在各极限状态下失效的概率均增大。此结果进一步表明不同服役龄期的钢框架结构的抗震性能是不同的,而且抗震性能随服役龄期的增长而退化。

6结论

本文基于腐蚀钢材材性试验结果及钢框架结构时变损伤模型,建立了多龄期钢框架结构易损性分析方法及步骤,并最终获得以结构整体损伤为抗震能力指标的不同服役龄期钢框架结构的易损性曲线。主要结论如下:

图6　不同龄期结构地震易损性曲线Fig.6　Seismic fragility curves of structures with different ages

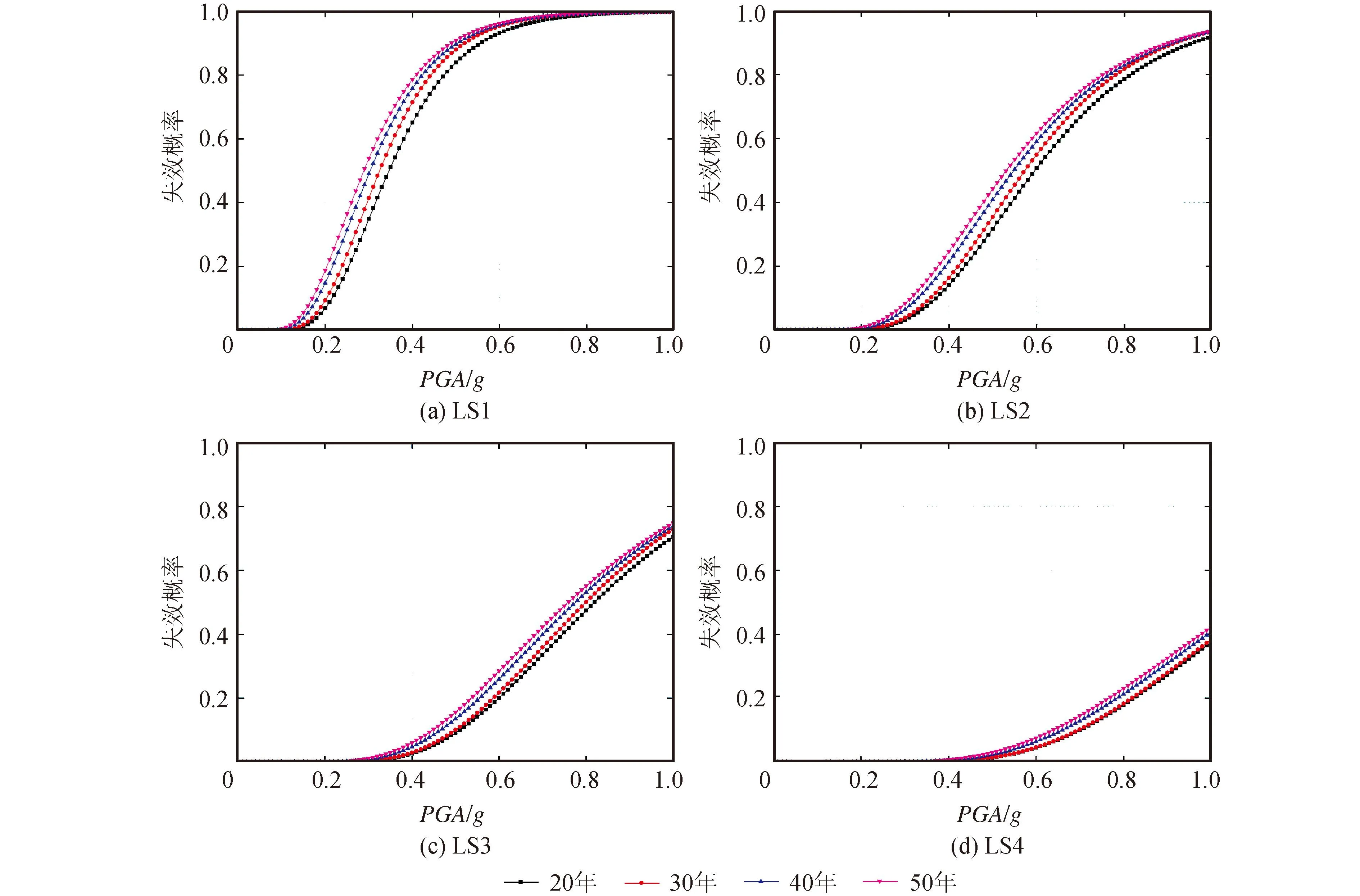
图7　某一特定极限状态下不同龄期结构地震失效概率对比Fig.7　Comparison between seismic failure probabilities of structures with different ages under a given limit state

(1) 考虑服役龄期对钢框架结构抗震性能的影响,分别建立概率时变地震损伤需求模型、概率时变抗震能力模型及时变易损性模型;

(2) 在对结构进行概率时变地震损伤需求分析时,考虑地震动与结构力学性能的不确定性,利用Monte Carlo法随机抽样产生不同服役时间的结构随机样本,每一服役时间的结构随机样本数要与地震波数量相同,再将地震波与结构样本随机搭配,生成相同数量的地震波-结构样本;

(3) 在概率时变地震损伤需求分析及抗震能力分析的基础上,得到多龄期(20年、30年、40年及50年)钢框架结构的易损性模型及易损性曲线。易损性曲线显示服役龄期增长将造成钢结构抗震性能的退化。

参考文献(References)

[1]万正东.RC框架结构基于概率损伤模型的地震易损性与风险分析[D].哈尔滨:哈尔滨工业大学,2009.

WAN Zheng-dong.Seismic Fragility and Risk Analysis of RC Frame Structures Based on Probability Damage Models[D].Harbin:Harbin Institute of Technology,2009.(in Chinese)

[2]李静,陈健云,温瑞智.框架结构群体震害易损性快速评估研究[J].振动与冲击,2012,31(7):99-103.

LI Jing,CHEN Jian-yun,WEN Rui-zhi.Fast Evaluation of Seismic Damage Group Vulnerability for a Frame[J].Journal of Vibration and Shock,2012,31(7):99-103.(in Chinese)

[3]郑山锁,王晓飞,程洋,等.锈蚀钢框架地震损伤模型研究[J].振动与冲击,2015,34(3):144-149.

ZHENG Shan-suo,WANG Xiao-fei,CHENG Yang,et al.Seismic Damge Model of a Corroded Steel Frame[J].Journal of Vibration and Shock,2015,34(3):144-149.(in Chinese)

[4]GB50046-2008,工业建筑防腐蚀设计规范[S].北京:中国计划出版社,2008.

GB50046-2008,Code for Anticorrosion Design of Industrial Constructions[S].Beijing:China Planning Press,2008.(in Chinese)

[5]GB/T15957-1995,大气环境腐蚀性分类[S].北京:中国标准出版社,1996.

GB/T15957-1995,Corrosivity Classification of Atmospheric Environment[S].Beijing:Standards Press of China,1996.(in Chinese)

[6]杨熙珍,杨武.金属腐蚀电化学热力学[M].北京:化学工业出版社,1991.

YNAG Xi-zhen,YANG Wu.Electrochemical Thermodynamics of Metal Corrosion[M].Beijing:Chemical Industry Press,1991.(in Chinese)

[7]刘新,时虎.钢结构防腐蚀和防火涂装[M].北京:化学工业出版社,2005.

LIU Xin,SHI Hu.Anti corrosion and Fireproof Costings for Steel Structures[M].Chemical Industry Press,2005.(in Chinese)

[8]张全成,吴建生,陈家光,等.近海大气中耐候钢和碳钢抗腐蚀性能的研究[J].材料科学与工程,2001,19(2):12-15,25.

ZHANG Quan-cheng,WU Jian-sheng,CHEN Jia-guang,et al.The Study on the Corrosion Resistance of Rust Layer on the Surface of Weathering Steel in Marine Atmosphere[J].Materials Science & Engineering,2001,19(2):12-15,25.(in Chinese)

[9]史炜洲.钢材腐蚀对住宅钢结构性能影响的研究与评估[D].上海:同济大学,2009:1-32.

SHI Wei-zhou.Investigation and Assessment of Influence of Steel Corrosion on Behavior of Residential Steel Structures[D].Shanghai:Tongji University,2009:1-32.(in Chinese)

[10]Lee H S,Noguchi T,Tomosawa F.FEM Analysis for Structure Performance of Deteriorated RC Structures due to Rebar Corrosion[C]/ / Proceeding of the International Concrete under Several Conditions Proceeding of the 2nd International Conference on Concrete under Severe Conditions.Tromso,Norway:E&FN Spon,1998:327-336.

[11]Cornell C A,Jalayer F,Hamburger R O,et al.The Probabilistic Basis for the 2000 SAC/FEMA Steel Moment Frame Guidelines [J].ASCE Journal of Structural Engineering,2002,128(4):526-533.

[12]吕大刚,于晓辉,潘峰,等.基于改进云图法的结构概率地震需求分析[J].世界地震工程,2010,26(1):7-15.

LV Da-gang,YU Xiao-hui,PAN Feng,et al.Probabilistic Seismic Demand Analysis of Structures based on an Improved Cloud Method[J].World Earthquake Engineering,2010,26(1):7-15.(in Chinese)

[13]FEMA P695,Quantification of Building Seismic Performance Factors[S].USA:Applied Technology Council,2009.

[14]郑山锁,田进,韩彦召,等.考虑锈蚀的钢结构地震易损性分析[J].地震工程学报,2014,36(1):1-6.

ZHENG Shan-suo,TIAN Jin,HAN Yan-zhao,et al.Seismic Fragility Analysis of Steel Structure Considering Steel Corrosion[J].China Earthquake Engineering Journal,2014,36(1):1-6.(in Chinese)

[15]于晓辉.钢筋混凝土框架结构的概率地震易损性与风险分析[D].哈尔滨:哈尔滨工业大学,2012.

YU Xiao-hui.Probabilistic Seismic Fragility and Risk Analysis of Reinforced Concrete Frame Structures[D].Harbin:Harbin Institute of Technology,2012.(in Chinese)

[16]Ellingwood B R,Kinali K.Quantifying and Communicating Uncertainty in Seismic Risk Assessment[J].Structural Safety,2009,31(2):179-187.

[17]吕大刚,于晓辉,王光远.基于FORM有限元可靠度方法的结构整体概率抗震能力分析[J].工程力学,2012,29(2):1-8.

LV Da-gang,YU Xiao-hui,WANG Guang-yuan.Global Probabilistic Seismic Capacity Analysis of Structures Based on Form Finite Element Reliability Method[J].Engineering Mechanics,2012,29(2):1-8.(in Chinese)

Seismic Vulnerability Analysis of Multiage Steel Frame Structures Based on Time-varying Seismic Damage Model

WANG Xiao-fei1, WANG Peng-fei1, JIA Hu1, ZHENG Wei-hua1, TIAN Jin2

(1.AcademyofCivilEngineering&Architecture,NanyangNormalUniversity,Nanyang473061,Henan,China;2.QingdaoInstituteofPublicArchitecturalDesignCo.Ltd,Qingdao266071,Shandong,China)

Abstract：In recent years, because of the frequency of earthquakes,steel has been widely used in the construction of civilian residential structures owing to its excellent seismic performance.However,considering that steel structures are widely used,there is a durability problem because of steel corrosion,which has become increasingly serious.Corrosion weakens steel member cross-sections and reduces steel's mechanical properties,ultimately affecting the seismic performance of steel structures.Seismic vulnerability analysis can be used to predict the damage probability at different levels of a structure under earthquakes of different magnitudes.As such,it has an important application value in seismic design,reinforcement,and maintenance decisions regarding structures.Seismic vulnerability research methods include empirical,testing,and analytical methods or a combination of two of these methods.For the most seismic hazard data,empirical vulnerability is the most accurate method,but not all areas experience an adequate number of earthquakes for researchers to obtain sufficient data to evaluate the structural damage probability at all levels.Experimental study methods of vulnerability analysis are also credible,but their costs are relatively high.Compared with the abovementioned two methods,an advantage of the analytical method of determining vulnerability is that it is a rapid and low-cost approach.The main factors that affect the seismic vulnerability of building structures are structural type,architectural age (including specifications and construction period of building design),intensity of fortification,site class,and number of layers.While research on the seismic vulnerability of various structures is quite mature,there has been scant consideration of the impact of service age on the seismic vulnerability of building structures or fragility curves of multiage structures.Based on the time-varying seismic damage model,we propose the use of an analysis method that includes the probabilistic seismic vulnerability steps of multiage steel frame structures under the corrosive action at an acidic atmospheric environment.We consider the influence of service age on the seismic performance of steel frame structures and establish the time-varying probabilistic seismic demand model,time-varying probabilistic seismic capacity model,and time-varying vulnerability model.Based on our analysis of the probabilistic seismic demand and probabilistic seismic capacity,we obtain a vulnerability model and vulnerability curve for multiage (20,30,40,and 50 years) steel frame structures.

Key words：multiage; steel frame structure; time-varying seismic damage model; vulnerability

DOI:10.3969/j.issn.1000-0844.2016.02.0192

中图分类号:TU391;TG172.3+1

文献标志码：A

文章编号:1000-0844(2016)02-0192-09

作者简介：王晓飞(1987- )，女，山东临沂人，讲师，从事建筑结构抗震研究。E-mail：wangxiaofei870102@163.com。

基金项目：校级专项项目(ZX2016009)；国家青年科学基金项目(11304168)

收稿日期:①2015-04-24