一种基于栅格的加权Voronoi图构建普适方法

刘 宝 举，刘 慧 敏，邓 敏，樊 子 德

(中南大学地球科学与信息物理学院地理信息系，湖南 长沙 410083)

一种基于栅格的加权Voronoi图构建普适方法

刘 宝 举，刘 慧 敏，邓 敏，樊 子 德

(中南大学地球科学与信息物理学院地理信息系，湖南 长沙 410083)

Voronoi图是空间分析的一个重要工具。该文将Voronoi区域视为流域，将栅格加权距离视为高程，提出一种顾及非空间属性的能够与ArcGIS无缝集成的Voronoi图生成方法。首先，根据Voronoi图的原始定义直接计算栅格的最小生成元加权距离，并仿D8算法思想，确定每个栅格的流向。然后，提取所有只有流出没有流入的栅格，并对栅格边界进行去噪处理和矢量化，得到Voronoi区域公共边，并生成附生成元属性的加权Voronoi图。最后，基于ArcEngine实现了任意生成元的带有非空间属性的加权Voronoi图。通过对比实验表明，该文所提出的方法能够高精度构建包含任意生成元的加权Voronoi图。

加权Voronoi图；加权距离栅格；流域；生成元

0 引言

Voronoi图是由俄国数学家M.G.Voronoi于1908年提出的一种空间分割算法，表达了在空间分布的若干要素对空间的最短距离剖分。Voronoi图最初用于解决计算几何的凸壳、Delaunay三角剖分、最小生成树等问题[1,2]，由于邻近性、邻接性等特殊性质，其应用迅速扩展到众多领域。而在地理信息学科，Voronoi图作为表达空间邻近关系与空间划分的有力工具，应用于地图综合[3,4]、空间邻近分析[5,6]、空间聚类分析[7]、空间关联规则挖掘[8]等方面。

从算法实现的数据模型角度，Voronoi图生成方法可以分为基于矢量和基于栅格两大类。矢量算法的提出比较早，算法也较多，大都是通过精确的数学计算得到垂直平分线，进而求取Voronoi图，最为典型的是增量构造法[9,10]。这类算法可以得到精准的边界线，时间和空间效率较高，但是其计算过程和数据结构复杂，并且不易于扩展到加权Voronoi图的生成[11]。栅格算法是基于生长元栅格按一定的距离模板向外扩张最终形成Voronoi图，具有代表性的是基于动态距离变换的方法[12,13]。以上算法都是从计算几何的角度出发，生成的Voronoi图不能很好地与GIS结合，限制了在地学领域的应用。近年来，Dong[14]和田松[15]等先后以开发组件的形式探讨了Voronoi图与GIS的集成。但文献[14]方法仅能处理单一生成元，而且Voronoi图有杂质面情况存在，文献[15]方法未考虑生成元的非空间属性，不利于Voronoi的空间分析。此外，ArcGIS软件中Cost Distance和Cost Allocation工具可以实现加权Voronoi图，但误差较大，不能准确体现生成元权重与Voronoi图的关系。为此，本文以shp格式矢量数据作为输入输出，研究了一种顾及非空间属性并能与GIS软件集成的高精度Voronoi图构建方法。

1 基于加权距离栅格的Voronoi图生成策略

利用加权距离栅格构建Voronoi图，首先从单个生成元入手，通过计算每个生成元的加权距离栅格，根据汇流思想可提取Voronoi栅格区域并获得栅格的生成元距离，同时保留生成元非空间属性特征，使之便于空间分析处理。在此基础上，通过Voronoi区域栅格边界锯齿消除算法，以提高生成Voronoi图的精度。

设S={p1,p2,…,pn}为二维欧氏空间(平面)上的点集，Voronoi图是根据最近距离原则对平面进行的一种分割，分割得到的每个区域内部包含一个点，并且区域内所有点到该点的距离均小于到其他点的距离，可表达为：

(1)

式中：d(p,pi)为点p与点pi之间的欧氏距离；点pi(i=1,2,…,n)称为生成元。

根据式(1)，则可得到每个要素的空间影响区域，它是对空间的一个完整划分，亦称为普通Voronoi图，如图1a所示。这种普通的Voronoi图不考虑属性对距离的影响。在实际应用中，每个要素对周围区域的影响程度通常不同。例如，同样是购物点，大商场比小商铺供货能力强，相应的正常服务范围更广。为此，需要构建加权Voronoi图，才能更好地体现每个要素在属性上的差异。

加权Voronoi图与普通Voronoi图的区别是在距离的设置上增加了一个权值(图1b)，可表达为：

(2)

式中：d(p,pi)为点p、pi之间的欧氏距离,i=1,2,…,n;λi为对应点元pi的权重。当λ1=λ2=…=λn时，则对应普通Voronoi图。加权Voronoi图可以很好地模拟不同级别地物的影响范围。

图1 普通Voronoi图和加权Voronoi图

Voronoi图作为一种具有特定结构的矢量多边形，公共边上的点到相邻生成元的距离或加权距离相等。因此，根据距离或加权距离确定Voronoi公共边是构建Voronoi的一个主要途径。距离生成元越远的区域，受到生成元的影响越小，且Voronoi公共边上的点受与之最邻近的两个生成元的影响相等，可见，Voronoi边是不同地物影响能力的等值线。如果对生成元的影响进行量化表达，并用栅格数据表示这种影响值，则可以很好地表示这种影响随距离增长而减小的趋势，这种栅格数据即是加权距离栅格。如图2所示，栅格距离值随着生成元的影响能力而逐渐变化，邻近两点间影响能力相等的栅格点形成线，即是要提取的Voronoi公共边。进而，加权Voronoi区域生成转化为加权距离栅格构建与Voronoi区域提取。

图2 生成元影响能力变化

2 加权距离栅格构建

2.1 单个生成元加权距离栅格计算

对区域进行栅格划分，并用生成元的加权距离表示栅格值，即为加权栅格距离。为构建加权距离栅格，需要从单个生成元入手，计算每一个生成元pi(i=1,2,…,n)的加权距离栅格fi(i=1,2,…,n)，然后将所有生成元的加权距离栅格依据特定关系进行叠加，获得所有生成元的加权距离栅格。

如图3所示，分别表示点、线、面状生成元影响下的加权距离变化。其中，xoy为栅格平面，z轴表示加权距离。加权距离的变化速度与生成元的权值直接相关，权值越大，倾角α越小，距离增长越缓慢，反之亦然。普通Voronoi图中所有生成元对应的α角为45°。随着权重的增大，倾角变小，生成元恒定距离以内的范围扩大。用一过点A且平行于z轴的平面切图3a所示的锥体，得到其纵切面图，如图4所示。图中AK的投影AP表示加权生成元A的影响区域，AK上任意一点D表示生成元A在投影位置C处栅格的加权距离为D的z坐标值。AF对应普通生成元的距离栅格，角β为45°，点E的z坐标值对应普通生成元A在栅格C处的距离值。

图3 单一生成元加权距离栅格示意

图4 单一点生成元加权距离投影

设d((x-x1),(y-y1))为普通距离函数，f(x,y)为加权距离函数，生成元A的权值为ωα，则有：

(3)

式中：x、y分别表示栅格位置坐标，x1、y1分别表示生成元坐标。类似地，可计算其他所有单个生成元的栅格加权距离fi(x,y),i=(1,2,…,n)。这种加权距离采用矢量欧氏距离获得，其精度始终保持在一个像元误差，与传统的依据距离模板扩散生长的模型相比精度更高，避免了因为方向不同产生距离不同和因为距离模板的选择而导致精度不统一的情形，亦保证了后续生成加权Voronoi图的精度。

一般地，要素的几何类型包括点状、线状和面状，对于线状要素，通常将其离散化为多个点进行处理；对于面状要素，首先设置其内部点的加权距离为0，然后将其边界离散化为多个点进行处理。

2.2 多生成元加权距离栅格确定

Voronoi图是多个生成元对区域的分割，如图5所示，多个生成元并存，在Voronoi图对区域的划分中，一个Voronoi区域的内部有且仅有一个对应的生成元，而Voronoi公共边处其所指向的相邻生成元加权距离相等。因此，在计算所有单个生成元的栅格距离值之后，需要确定最小的加权距离，即：

F(x,y)=min(fi(x,y)),i=(1,2,…,n)

(4)

图5 多个生成元距离栅格示意

图6 加权距离栅格示意

3 加权Voronoi区域提取

3.1 区域栅格划分

如图7所示，将栅格加权距离视为高程[16]，由于生成元处的栅格距离值为极小值0，因此，水流汇聚点即为生成元，而汇聚到同一生成元的栅格区域对应该生成元的流域，即Voronoi区域，而相邻流域的分水岭即为Voronoi区域边界，从而，提取出流域并将其转换为矢量面就可以获得相应的Voronoi图。为提取流域信息，需要确定各位置的水流方向，即每个栅格像元水流流出的方向，进而获得水流汇聚情况。

图7 加权距离栅格

引入D8算法思想，按八邻域划分方向，并按照2n(n=0,1,…，7)对八邻域进行编码，如图8所示。根据每个加权距离栅格像元与周围八邻域像元的距离梯度，确定最陡下降方向，作为该栅格的流向，并用流向编码中表示该方向的值对输出像元进行编码，由此，得到流向栅格。然后，从生成元栅格开始逆向搜索汇入栅格，归属为对应的流域，直至为每个栅格分配唯一流域，即可得到流域栅格，完成Voronoi区域划分。

图8 流向编码

Voronoi图是空间分析的重要工具，空间信息和非空间属性信息是空间分析的两个基础，附属非空间属性的Voronoi图更利于空间分析。为此，进行Voronoi区域划分后，为每一个Voronoi面赋予对应生成元的非空间属性，生成带属性值的矢量面结构。

3.2 边界处理

在对每一个栅格确定流域的过程中，由于某些位于分水岭上的特别是多流域交叉点处的栅格的流域归属无法准确确定，所以在将栅格区域转换为矢量格式过程中，某些结点或边界处会生成如图9a所示的杂质面，这种杂质面只有一个像元大小，但形成了区域空洞，同时影响基于Voronoi图的统计分析，因此，有必要在转换为Voronoi区域之前对流域栅格边界进行杂质面去除处理。

分析发现，在流域分区栅格中，当边界上的中心像元与上下左右四邻域像元值均不相同时，会产生杂质面，按照四邻域像元值是否相同分为4种情形，即四邻域分别取2种、3种和4种值的情况，如图10所示。对于四邻域对向相同的情形，如图10e所示，表示汇水流域或Voronoi区域交叉，与实际情形不符，不予考虑。针对图10a-图10d所示的四邻域模板及其旋转形式，用邻域栅格代替中心像元，其中：图10b与图10c所示情形用a代替，图10a所示情形用a或b代替，图10d所示情形用a、b、c、d任一值代替，使得Voronoi图边界存在一个像元的误差。经过代替处理后，转换得到的矢量Voronoi图不包含杂质面，锯齿效应亦得到明显改善，如图9b所示。

图9 流域栅格处理前后生成的Voronoi图

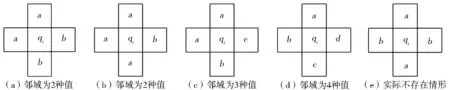
图10 中心像元与四邻域值不同的情形

由以上步骤，通过对研究区域的栅格划分，生成任意生成元的加权距离栅格，根据流域思想提取Voronoi边界，并对Voronoi图进行边界处理，生成加权Voronoi图，最后将生成元专题属性关联到Voronoi图中。这种带有非空间属性的Voronoi图可以直接用于空间分析处理，扩展了其应用。

4 实验与分析

4.1 方法验证

为了验证本文方法的有效性，首先用一组模拟的任意生成元进行实验。如图11所示，该组生成元包括点、线、面3类不同要素，并被赋予不同的权值。采用本文方法，构建其加权Voronoi图(图11b)，并输出加权距离栅格(图11c)。从图中可以看出，本文方法能够生成不同类别生成元的加权Voronoi图，然而，划分栅格的大小不可避免地影响Voronoi图的精度并导致边界的锯齿效应。在计算效率方面，由于涉及处理过程较多无法准确给出时间复杂度，但通过实验证明在250*250的栅格大小情况下，构建包含50个生成元的Voronoi图所耗费时间为50 s左右(i3，2.27GHz，2GB RAM)，随着栅格分辨率的变大，耗费时间也会有所增加。

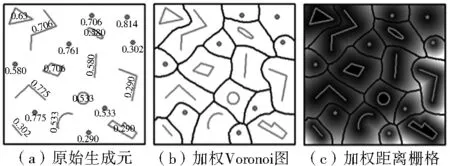
图11 不同生成元加权Voronoi图

为定量分析本文方法的精度效果，设计了第二组实验来检验本文方法的精度。如图12所示，采用6组点状分布生成元数据，每组数据包含14个随机点，用本文方法构建其等权Voronoi图，将其与普通Voronoi图进行对比，选取对应的Voronoi区域的面积误差百分比作为精度评价指标，对本文方法的精度进行检验。表1列出了由6组实验数组计算得到的平均误差与最大误差。从表中可以看出，本文方法的平均误差均在1%以下，具有较高的精度。本文方法在计算栅格距离时，直接采用普通距离作为基准，再进行加权掩膜，与传统的依据距离模板扩散生长的模型相比，避免了栅格距离与生成元方向相关而导致精度不统一的问题，从而提高了最终Voronoi图的精度。需要补充说明的是，可结合应用需要设定加权距离栅格的大小，精度要求越高，设定栅格越小，分辨率的提高还可以有效地避免多生成元共面的情形。

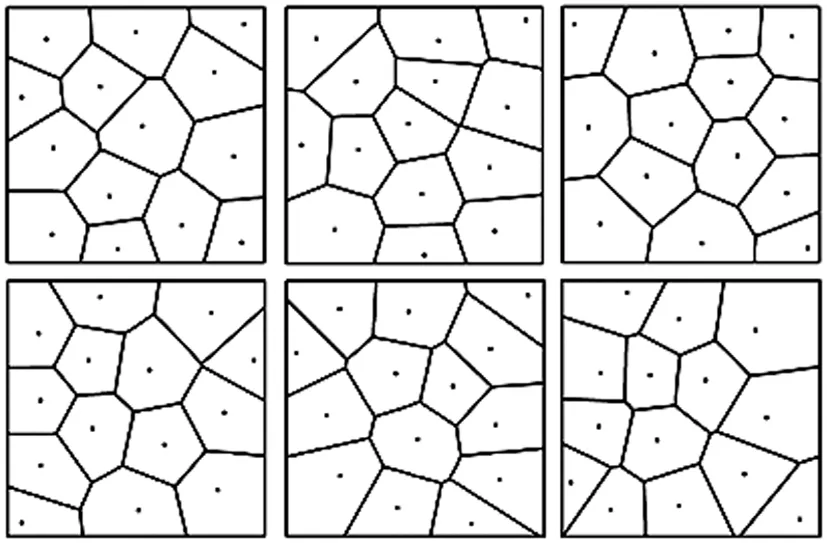
图12 6组随机数据生成的普通Voronoi图

表1 面积误差率

Table 1 Area error rate

第一组第二组第三组第四组第五组第六组最大误差1.788%0.893%1.044%1.558%1.202%0.887%平均误差0.590%0.352%0.462%0.579%0.421%0.336%

4.2 对比分析

ArcGIS中的Cost Distance和Cost Allocation工具也可以实现加权Voronoi图，为了比较其与本文方法的差异，采用图1所示数据进行对比实验，生成结果如图13所示，上标数字表示权重。由于加权距离栅格本身就体现了生成元的影响范围，所以本文方法直接提取加权距离栅格中“分水岭”作为Voronoi边界，而ArcGIS方法通过统计加权距离栅格中各像元到邻近生成元的最小加权距离以确定像元归属，即Voronoi边界上像元到邻近两个生成元的加权距离相等，由于生成元权重和影响范围呈正比，因此这种累加距离必然导致Voronoi边相对靠近权值较大的生成元，弱化了相对重要生成元的影响力。所以当相邻生成元权重相差比较大时，本文方法生成的Voronoi图能够更加准确地体现不同权重生成元的影响区域。

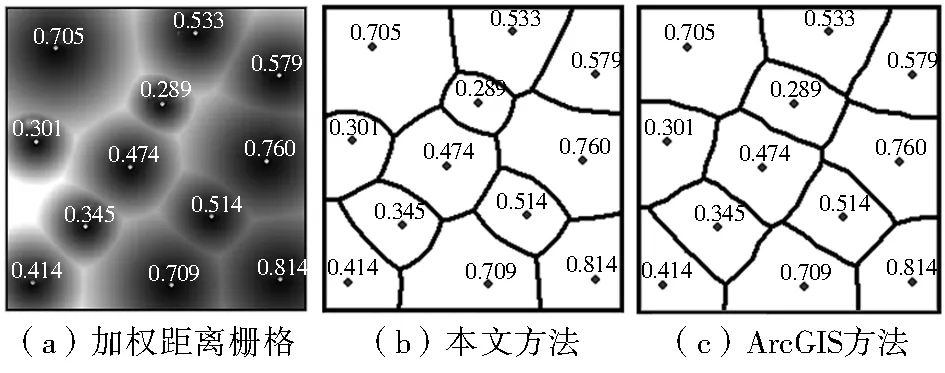
图13 不同方法生成加权Voronoi图

Voronoi图与GIS软件的结合是Voronoi图生成方法广泛推广应用的重要前提，本文基于ArcEngine实现了能够与GIS软件完全集成的Voronoi构建过程。与文献[14]的方法相比，本文方法可以生成任意生成元及其组合的加权Voronoi图，与文献[14]的方法仅能处理单一生成元的情况。为了验证两种方法在实际应用中的效果，采用2013年中国西部七省3.5级以上地震分布点数据作为验证数据，震级作为生成元权重。结果如图14所示，两种方法生成的加权Voronoi图大致相同，但是在细节处理上文献[14]方法生成的Voronoi图在部分边界上有杂质面产生，需要采用本文边界处理方法对其进一步优化处理方可得到平滑边界。

图14 中国西部2013年3.5级以上地震分布Voronoi图

5 结论

本文结合Voronoi图的结构特性，从其基本定义出发，利用普通距离栅格与生成元权值掩膜运算构建加权距离栅格，进而提出了一种加权Voronoi图生成的普适方法，避免了在欧氏距离下扩散模板的选择导致的精度不统一问题[13]，使整个Voronoi图保持同一精度，并有效解决了许多栅格方法存在的锯齿问题。同时，此方法可以与GIS软件完全集成，顾及非空间属性和伴生加权距离栅格的特性使得该方法得到的结果可直接用于GIS的空间分析处理。实验证明，与现有方法相比，本文方法精度高，能够处理任意种类生成元，并且与GIS软件无缝集成，同时有效避免了矢量算法的结构复杂性。另外，该方法产生的任意中间数据和最终生成的加权距离栅格、Voronoi图都可以直接作为软件输入数据进行后续处理。然而，对于各生成元的权重差异很大的情形，还不能较好地生成多孔洞形态的Voronoi图;其次，算法的效率依然较为低下，生成效率和栅格精度难以兼顾，今后需进一步研究其效率优化问题，使其能在精度和效率方面得到共同提高。

[1] OKABE A,BOOTS B,SUGIHARA K,et al.Spatial Tessellations:Concepts and Applications of Voronoi Diagrams[M].2nd,New York:Wiley Press,2000.

[2] DU Q,FABER V,GUNZBURGER M.Centroidal Voronoi tessellations:Applications and algorithms[J].SIAM Review,1999,41(4):637-676.

[3] 闫浩文,王邦松.地图点群综合的加权 Voronoi 算法[J].武汉大学学报(信息科学版),2013,38(9):1088-1090.

[4] 李佳田,康顺,罗富丽.利用层次 Voronoi 图进行点群综合[J].测绘学报,2014,43(12):1300-1306.

[5] LI Z L,HUANG P Z.Quantitative measures for spatial information of maps[J].International Journal of Geographical Information Science,2002,16(7):699-709.

[6] 刘慧敏,邓敏,樊子德,等.地图上居民地空间信息的特征度量法[J].测绘学报,2014,43 (10):1092-1098.

[7] YAN H W,WEIBEL R.An algorithm for point cluster generalization based on the Voronoi diagram[J].Computers & Geosciences,2008,34(8):939-954.

[8] 李光强,邓敏,朱建军.基于 Voronoi 图的空间关联规则挖掘方法研究[J].武汉大学学报(信息科学版),2009,33(12):1242-1245.

[9] 张有会.加权 Voronoi 图画法的研究[J].计算机科学,2001,28(6):126-128.

[10] GONG Y,LI G,TIAN Y,et al.A vector-based algorithm to generate and update multiplicatively weighted Voronoi diagrams for points,polylines,and polygons[J].Computers & Geosciences,2012,42:118-125.

[11] LETSCHER D.Vector Weighted Voronoi Diagrams and Delaunay Triangulations[C].Proceedings of the 19th Annual Canadian Conference on Computational Geometry.2007.

[12] 李成名,陈军.Voronoi 图生成的栅格算法[J].武汉测绘科技大学学报,1998,23(3):208-210.

[13] CHEN J.A raster-based method for computing Voronoi diagrams of spatial objects using dynamic distance transformation[J].International Journal of Geographical Information Science,1999,13(3):209-225.

[14] DONG P.Generating and updating multiplicatively weighted Voronoi diagrams for point,line and polygon features in GIS[J].Computers & Geosciences,2008,34(4):411-421.

[15] 田松,崔希民,孙云华,等.顾及障碍物的一般图形 Voronoi 图及其加权图的 ArcGIS 栅格实现[J].地理与地理信息科学,2014,30(4):42-45.

[16] 艾廷华,禹文豪.水流扩展思想的网络空间Voronoi图生成[J].测绘学报,2013,42(5):760-766.

A General Raster-Based Approach for Generating Weighted Voronoi Diagrams

LIU Bao-ju,LIU Hui-min,DENG Min,FAN Zi-de

(DepartmentofGeographicInformatics,CentralSouthUniversity,Changsha410083,China)

Voronoi diagram plays a very important role in spatial analysis.Existing methods of generating Voronoi diagrams seldom consider the effect of non-spatial attributes,in this case the partition of geographical space is inconsistent with human cognition.To solve this problem,a unified raster-based algorithm is presented for generating weighted Voronoi diagrams in this paper.First,the region is divided into a set of small regular grids,and the weighted distance of each grid generator is calculated based on the original definition of Voronoi diagram.Second,flow direction of each grid is calculated by using an eight direction (abbreviated as D8) flow model,where the weighted distance is regarded as the elevation and the Voronoi region as being a basin.In this situation,the collection of grids which has no any inflow consists of the extract common edges of adjacent Voronoi regions.The weighted Voronoi diagrams are further built with a modification of the common edges by considering non-spatial attributes,which is implemented by means of ArcEngine software.Finally,practical examples are provided to illustrate the advantages of the proposed method in this paper,compared with current methods.

weighted Voronoi diagram;weighted distance grid;watershed;generator

2015-11-23；

2016-04-05

国家自然科学基金项目(41301515)；地理空间信息工程国家测绘地理信息局重点实验室经费资助项目(201413)；中国博士后科学基金(2014M562134)

刘宝举(1989-)，男，硕士研究生，主要从事GIS空间分析研究。*通讯作者 E-mail：lhmgis@163.com

10.3969/j.issn.1672-0504.2016.04.004

P208

A

1672-0504(2016)04-0017-06