一种具有约束的CRM区间回归方法

郭均鹏，赵 茹，李汶华



一种具有约束的CRM区间回归方法

郭均鹏，赵 茹，李汶华

（天津大学 管理与经济学部，天津 300072）

CRM（Center-Range Method，中点半径法）是求解区间数据回归模型的常用方法，其通过分别拟合区间中点和半径进行求解。研究了CRM方法的不足，当区间的中点波动比较大，而区间半径相对较小时，拟合中点和半径可能会导致许多预测区间与样本区间没有任何重叠。针对该问题，在CRM方法基础上，考虑在中点及半径误差平方和最小化的同时，增加一些约束条件，提出一种改进的区间回归方法。对区间回归分析的评价指标进行了研究，主要有均方根误差、决定系数、比率三个方面，选取这些指标用于本文所提出的约束方法的评价。通过蒙特卡洛模拟对约束方法进行评价，并选取2013年5月至2013年6月的沪深300指数和华夏上证50ETF构建区间样本数据，进行实证分析。模拟实验和实证分析都表明约束方法能够有效的减少预测区间和样本区间无任何重复的样本数目，在平均准确率和观测区间包含的预测区间的平均比率方面也具有明显的优势。

回归分析；区间数；约束；中点半径法（CRM）

0 引言

研究因变量与自变量之间的关系，是数据分析、模式识别、数据挖掘、机器学习等许多问题的一个重要任务[1]。回归分析是一种常用的确定因变量与自变量关系的分析方法。传统的回归分析研究，主要是针对传统点数据进行的。近年来，许多学者从模糊数学[2-12]、区间型符号数据分析[13-18]、计算机科学[19]等不同角度，对更为复杂的、涉及到模糊数的情况进行研究。区间数也是一种模糊数，目前区间回归分析已有许多应用[20-22]。

Tanaka et al.[2]最早提出了模糊线性回归的模型及求解方法。模型中的自变量是点数据，因变量和系数是三角模糊数，通过最小化系数的宽度，同时约束预测区间按某种置信水平完全覆盖样本区间，求解一个线性规划来估计模型系数。该方法主要有三个缺陷[3]：一是许多预测系数的半径为零；二是模型的解具有参考点依赖性，当用自变量减去其均值代替原自变量进行回归时，估计系数会发生很大的变化；三是要求置信水平的预测区间完全覆盖该置信水平的样本区间，导致当存在半径较大的观测区间或是存在异常值时，估计系数的宽度也会较宽。针对这些问题，文献[4-6]等提出了不同的改进方法。Sakawa和Yano[7]、Hojati et al.[3]考虑了所有数据均是模糊数的情况。Chen 和 Hsueh[8]基于一种距离准则[23]提出一种数学规划方法，能有效的减少总估计误差，但是当数据量较多时运算效率明显下降。Chen和Hsueh[9]通过取模糊数的截集，将模糊数转化成数值区间，进而通过最小化预测区间与样本区间左右端点差值的平方和求解。Hladíl和Černý[10]提出了一种基于误差分析的回归方法，首先通过传统的针对点数据估计点系数的方法确定区间系数的中点，进而确定半径，将系数扩展成一个区间。该方法根据自变量、因变量的数据类型，进行了三类探讨：自变量和因变量都是点数据；自变量为点数据、因变量为区间数据；自变量和因变量都是区间数据。该方法适用于多种类型的数据，但是需要给误差率设定一个初始值，排除异常值时也是通过主观分析进行，这些导致方法具有不确定性，且难以确定最优结果。李汶华等[22]从误差传递的理论出发,研究基于误差传递的区间型符号数据的回归分析方法。Boukezzoula et. al.[11]为观测数据的中点和半径分别建立模型定义域，作为规划模型的一个约束，提出了一种中点-半径回归方法。

符号数据分析（symbolic data analysis,SDA）[24]通过“数据打包”，实现数据降维，从而实现了对海量数据的快速分析、处理。区间数据是一种常用的符号数据，针对区间型符号数据的回归研究也取得了许多成果。Billard 和 Diday[13]首先提出了线性拟合区间型符号数据的方法，称为CM（Center Method）方法。该方法假设区间的上限、下限具有相同的系数，区间上限、下限的误差和作为区间数的误差，通过最小化误差平方和求解系数。Billard 和 Diday[14]将区间上限、下限分别回归，提出了MinMax方法，从而将一个区间回归问题转化为两个点回归问题。文献[13]中区间的中点和半径是同时考虑的，Lima和Carvalho[1]提出了一种CRM（Centre and Range Method）方法，分别估计区间的中点和半径。CRM方法不能保证区间右端点一定大于左端点，因此，Lima和Carvalho[15]提出了CCRM（Constrained Center and Range Method），在对半径误差进行最小化时，保证半径的系数非负，由于半径是非负的，因此预测的半径也是非负的，从而保证了预测区间的合理性。González-Rodríguez et al.[16]在保证Hukuhara difference[25]存在的情况下，提出了针对区间数的简单线性回归方法。Blanco-Fernández et al.[17]提出一种新的回归模型M，进而给出了模型求解方法。

中点半径法（Midpoint-Radius，MR）和端点法（Endpoint，EP）是区间数据的两种表达方式[11]。相比于EP表达方式，MR方式有许多优势[11]：区间的不确定性（半径）与区间的变化趋势（中点）相分离、许多实际情况中MR表达方式更为自然等。Blanco-Fernández et al.[17]提出的模型M也可看作是采用了MR表达方式，该模型用一个表达式将区间数据的不确定性和变化趋势表示出来。该模型的不足在于，将模型M转化为一般表示方法，即区间数据中点关系和半径关系分别表达时，可知半径关系中的系数和常数项都必须是正值，而实际情况不一定都是如此。CRM、CCRM方法通过分别拟合区间中点和半径进行求解，但是当区间的中点波动比较大，而区间半径相对较小时，拟合中点和半径，会有许多样本区间分布于回归曲线两侧，且与回归曲线有较大的偏离，这可能会导致预测区间与这些偏离回归线较远的样本区间没有任何重叠。以表1中所示数据为例，其对应的样本区间及预测区间如图1所示。可以看出，10个数据中有3个数据的预测区间与样本区间没有任何重合。

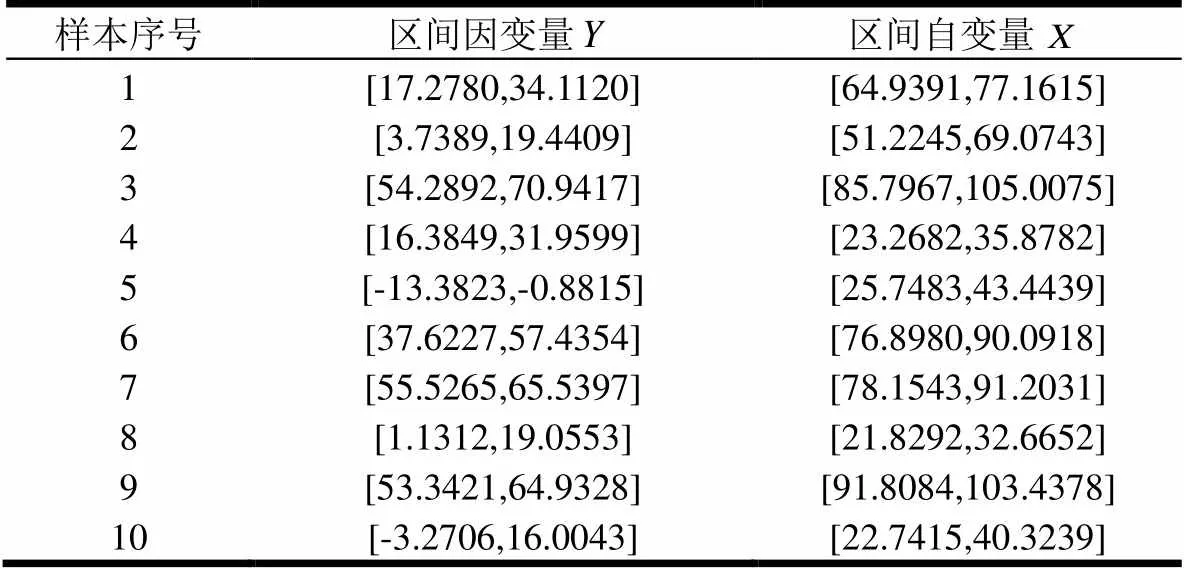
表1 示例数据

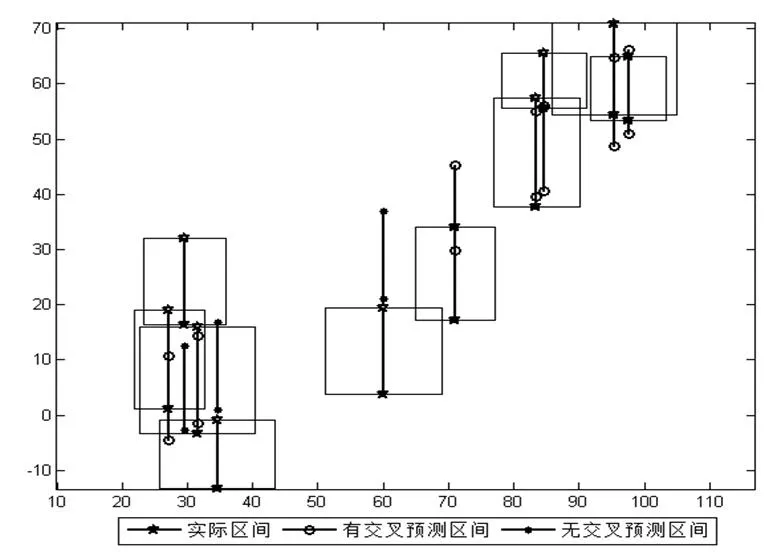
图1 示例数据矩形图

基于上述分析，本文选取中点关系、半径关系分别表示的模型，在CRM方法的基础上，考虑增加一些约束条件，提出一种具有约束的回归方法。为此先对CRM方法进行简介。

1 CRM方法简介

（2）

通过最小化中点及半径误差的平方和求解，如式（3）所示。

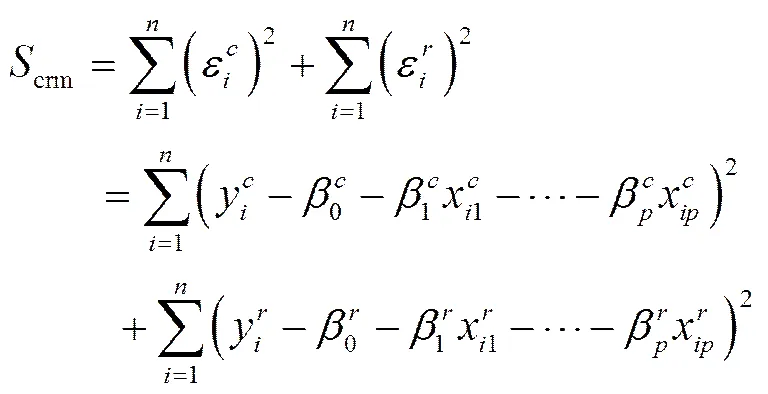
式（1）、（2）也可以用式（4）、（5）表示，其中

，，，，，，

（4）

（5）

（7）

2 一种新的具有约束的回归方法

由引言部分分析可知，M方法不能有效的表达半径线性关系中常数项为负的情况，因此本文选择CRM方法中的模型，即分别构建区间数据中点和半径的线性关系，如式（1）、（2）所示。为使预测区间与样本区间尽可能有重叠，考虑在约束中点及半径误差平方和最小化的同时，增加一些约束条件。Tanaka et al.[2]提出的方法中，要求置信水平的预测区间完全覆盖该置信水平的样本区间，这往往会导致预测区间过大。此外，该方法适用于回归系数、因变量为模糊数、自变量为点数据的情况。本文构建的模型中，自变量和因变量均为区间数据，系数为点数据。为避免预测区间过大，本文适当放松约束条件，拟合时只要求预测区间与样本区间有交叉，而不需要全部覆盖。CCRM方法也是在CRM方法的基础上增加了一些约束条件，但CCRM方法主要是解决预测区间不合理现象，即左端点大于右端点的情况，而本文中的约束方法主要解决的是预测区间与样本区间无交叉的情况。

（8）

其中的约束条件保证了观测样本的预测区间和样本区间有所交叉。和分别是一系列样本的预测区间的右端点和相应的左端点，和分别是相应的观测区间的左端点和右端点，约束条件表明，对于所有样本，都有预测区间右端点值大于或等于相应观测区间左端点值，同时预测区间左端点值小于或等于相应观测区间右端点值，因此约束条件保证了所有样本的观测区间和预测区间有所交叉。

3 模型评价

3.1 评价指标

3.1.1 均方根误差

均方根误差（Root Mean-Square Error，RMSE）是评价区间线性回归方法时常用到的一个指标， Lima和Carvalho[1]分别计算了区间上限和下限的均方根误差，即、，李汶华等[22]基于Hausdorff距离[27]提出一种均方根误差，Chuang[19]同样基于Hausdorff距离[27]，提出了一种区间数的均方根误差计算方法。Bargiela[12]针对模糊数，考虑模糊数的最小值、最大值和中值，提出了一种计算均方根的方法。

3.1.2 决定系数

Lima和Carvalho[1]分别计算了区间上限和下限的相关系数、，Lima和Carvalho[15]针对区间中点和半径分别表达的模型，提出了三种可能的决定系数计算方法。

3.1.3 比率

Hu和He[18]定义了准确率的概念，此外还统计了预测准确率为零的样本的数目。Mehran et al.[3]提出可以通过计算预测区间包含的观测区间的比率，以及观测区间包含的预测区间的比率，来衡量预测区间与观测区间的覆盖程度。

此外，本文还统计了每组数据预测准确率为0的平均样本数目，用表示。

3.2 蒙特卡洛模拟

3.2.1 数据形成

3.2.2 模拟实验

表2 蒙特卡洛模拟的几种情况

实验时，首先生成一组系数，然后生成500组自变量的中点，结合生成的系数，再加上误差项，生成因变量的中点，最后生成因变量及自变量的半径，从而形成500组模拟数据。随机选择其中400组数据作为训练集估计系数，100组作为测试集进行预测，将预测区间与样本区间进行比较，计算三个评价指标。为避免一次模拟的偶然性，重复生成500组模拟数据并计算评价指标的过程100次，进而可以求得100组评价指标，可以对这些指标进行T检测，评价方法在不同方面的优劣性。为避免系数导致的偶然性，再重新生成一组系数，重复上述过程，这样总共进行50次。

3.2.3 实验结果

本文通过T检测对方法进行比较，显著水平为1%。若以方法A不优于方法B为零假设，方法A优于方法B为备择假设，则对于指标，值越大说明方法越差，因此，。而对于和两个指标，值越大说明方法越好，因此，，以及，。若假设方法A和B相同，则零假设为方法A与方法B的指标值相同，备择假设为不相同。表3-表6分别是以约束方法优于、劣于、等同于CRM方法作为原假设进行T检测的结果。

在C2情况下，从表3可以看出，三个指标的拒绝率都在50%以上，时、的拒绝率高达100%，而时的拒绝率也达到了96%，的拒绝率为100%，从表4可以看出，三个指标的拒绝率都是0，说明在各个方面，约束方法都优于CRM方法。再比较表5可以看出，时两方法在均方差误差方面不相同的概率为52%，时为60%，而在、两指标方面大多都是100%。综合三个表的结果可以看出，在、两方面，约束方法都优于CRM方法，在方面，50%以上的情况下，约束方法具有优势，其余情况下，两者基本相同，综合来看，约束方法优于CRM方法。

在C3情况下，从表5可以看出，三个指标的拒绝率都是100%，说明这种情况下，两个方法在所有指标上都不相同，从表3、4可知，、两方面，约束方法表现更佳，而在方面，CRM方法更佳，两者各有优劣。

表6、7分别为C2、C3情况下，以固定参数随机生成的10组实验数据统计的数目。当时，时。通过对比表6、表7可以发现，在C3情况下，也就是误差的变化范围相对于中点的变化范围较大时，通过本文中的约束方法进行预测，能够预测出更多的和样本区间有所交叉的区间，而用CRM方法进行预测，则有约20%以上的预测区间与样本区间没有任何交叉，准确率为0。

综上所述，当区间中点的波动相对于区间宽度较小时，约束方法与CRM方法基本一致；当区间中点的波动相对于区间宽度适中时，约束方法在各方面都优于CRM方法，在预测准确率为0的样本区间数目方面有轻微的优势；当区间中点的波动相对于区间宽度较大时，约束方法在区间均方根误差方面不及CRM方法，但在平均准确率和样本区间包含预测区间的平均比率方面，约束方法都具有明显的优势，在预测准确率为0的样本区间数目方面更具是显著的优势。

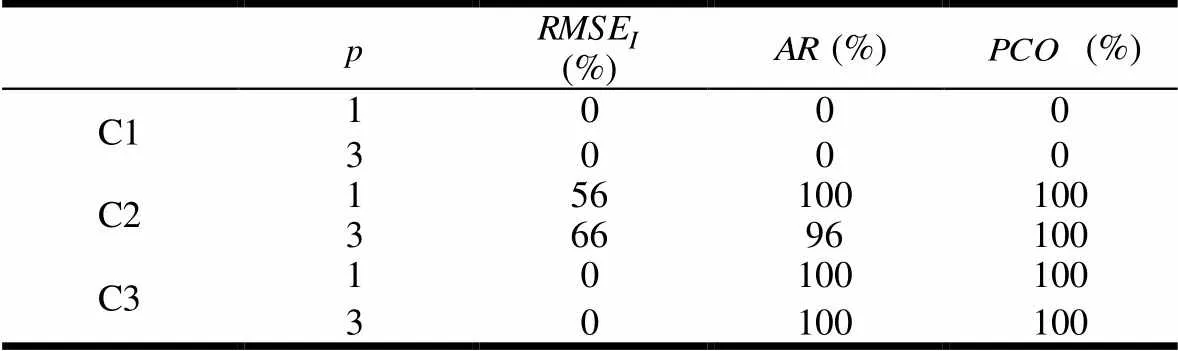
表3 为以约束方法优于CRM方法作为原假设的实验结果

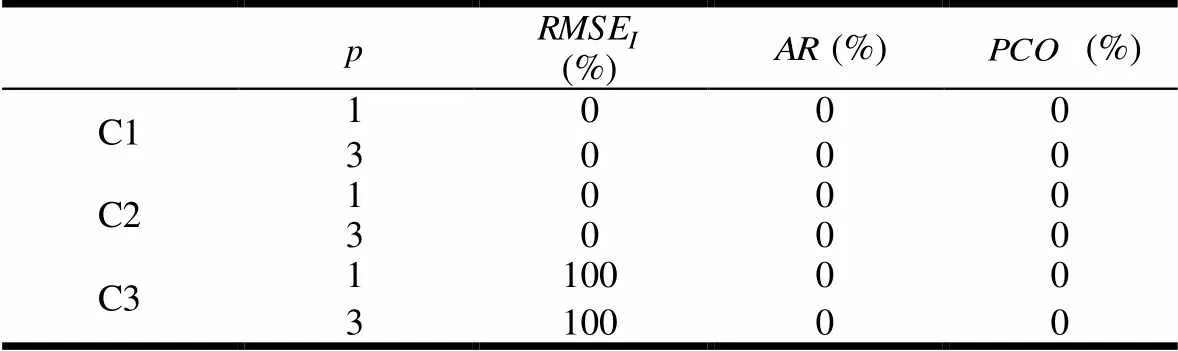
表4 为以CRM方法优于约束方法作为原假设的实验结果

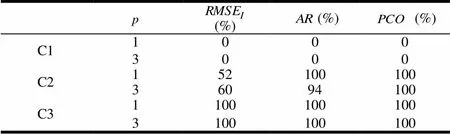
表5 为以CRM方法等同于约束方法作为原假设的实验结果

表6 C2情况下用CRM和约束方法对10组模拟数据进行回归预测的统计结果

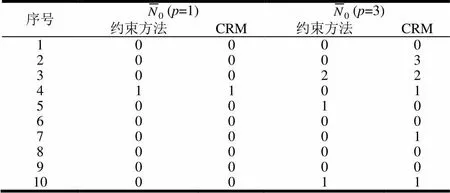
表6 C2情况下用CRM和约束方法对10组模拟数据进行回归预测的统计结果

序号(p=1)(p=3) 约束方法CRM约束方法CRM 10000 20003 30022 41101 50010 60000 70001 80000 90000 100011

表7 C3情况下用CRM和约束方法对10组模拟数据进行回归预测的统计结果

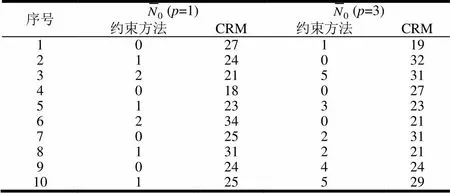
表7 C3情况下用CRM和约束方法对10组模拟数据进行回归预测的统计结果

序号(p=1)(p=3) 约束方法CRM约束方法CRM 1027119 2124032 3221531 4018027 5123323 6234021 7025231 8131221 9024424 10125529

4 实证研究

在进行股指期货套利时，需要通过间接方法，构建现货头寸进行套利交易[28]。ETF基金能够用于构建现货组合，文献[28]的研究表明沪深300指数收益率与华夏上证50ETF、华安上证180ETF等几个基金的收益率具有高度相关性，因此猜测沪深300指数与华夏上证50ETF之间也具有较高的相关性。本文选取2013年5月至2013年6月两个月中每天的沪深300指数与华夏上证50ETF的最大值、最小值作为样本数据，构建区间数据，研究两者之间的线性关系。图3是用样本数据绘制的矩形图，两者之间的线性关系比较明显。

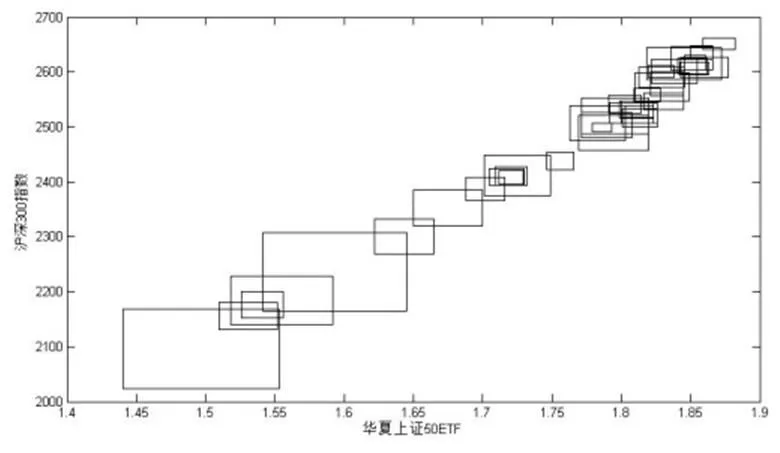
图3 沪深300指数与华夏上证50ETF区间样本矩形图

以沪深300指数区间样本为因变量，以华夏上证50ETF为自变量，分别用CRM方法和约束方法进行区间回归，求得的回归方程如下：

图4、图5分别为用CRM方法和约束方法进行预测的结果，为了避免数据过多导致难以通过图像区分数据，只绘制了15组数据。从图形上看，两个方法预测结果差别不大，都能很好的拟合样本数据。

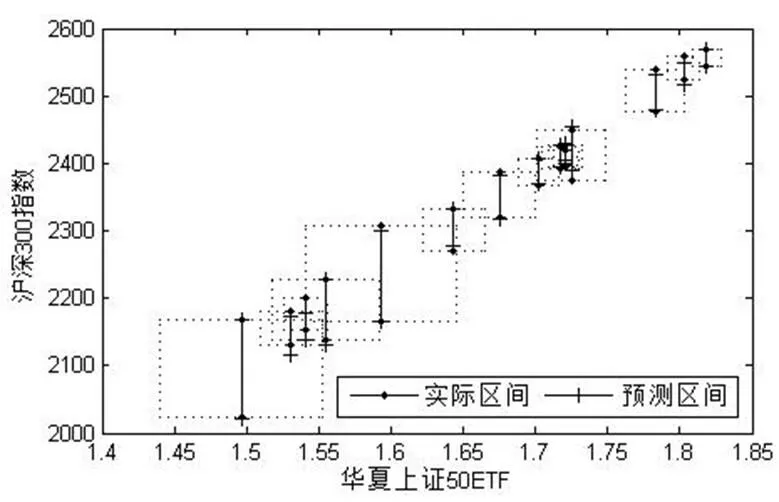
图4 CRM方法预测结果图

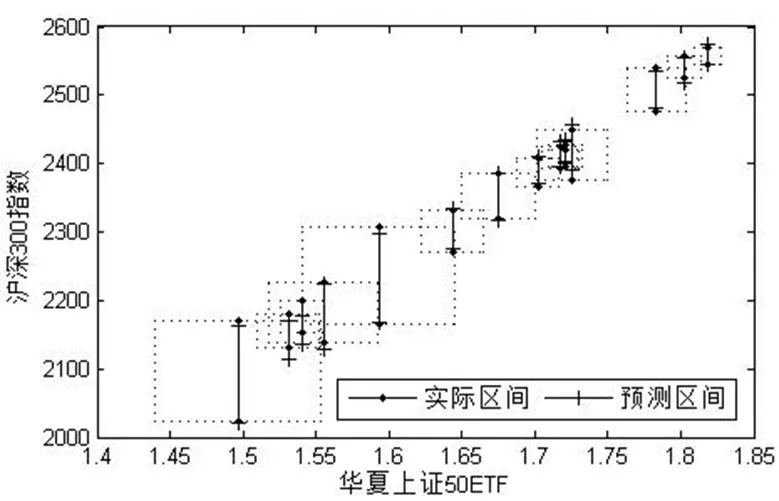
图5 约束方法预测结果图

表8 CRM方法与约束方法回归预测效果评价指标结果

5 结论

本文通过添加约束，对CRM方法进行了改进，以解决区间中点波动较大，而区间半径又相对较窄时，许多预测区间与样本区间没有任何重叠的问题。蒙特卡洛模拟实验以及基于股票市场的实证分析，都显示出了约束方法所具有的优越性。

本文的研究工作有如下可能的研究方向：

（1）当区间样本中存在异常值时，会严重影响预测效果，因此研究如何排除异常值也很有研究意义。

（2）如何在保证预测区间与样本区间尽可能重叠的同时兼顾均方根误差，实现两者之间的平衡。

[1] Lima Neto EA, de Carvalho FAT. Centre and Range method for fitting a linear regression model to symbolic interval data[J]. Computational Statistics & Data Analysis, 2008, 52(3): 1500-1515.

[2] Tanaka H, Uejima S, Asai K. Linear regression analysis with fuzzy model[J]. IEEE Trans. Systems Man Cybern, 1982, 12: 903-907.

[3] Hojati M, Bector CR, Smimou K. A simple method for computation of fuzzy linear regression[J]. European Journal of Operational Research, 2005, 166(1): 172-184.

[4] Savic DA, Pedrycz W. Evaluation of fuzzy linear regression models[J]. Fuzzy Sets and Systems, 1991, 39(1): 51-63.

[5] Tanaka H, Ishibuchi H. Identification of possibilistic linear systems by quadratic membership functions of fuzzy parameters[J]. Fuzzy sets and Systems, 1991, 41(2): 145-160.

[6] Tanaka H, Hayashi I, Watada J. Possibilistic linear regression analysis for fuzzy data[J]. European Journal of Operational Research, 1989, 40(3): 389-396.

[7] Sakawa M, Yano H. Multiobjective fuzzy linear regression analysis for fuzzy input-output data[J]. Fuzzy Sets and Systems, 1992, 47(2): 173-181.

[8] Chen LH, Hsueh CC. A mathematical programming method for formulating a fuzzy regression model based on distance criterion[J]. Systems, Man, and Cybernetics, Part B: Cybernetics, IEEE Transactions on, 2007, 37(3): 705-712.

[9] Chen LH, Hsueh CC. Fuzzy regression models using the least-squares method based on the concept of distance[J]. Fuzzy Systems, IEEE Transactions on, 2009, 17(6): 1259-1272.

[10] Hladík M, Černý M. Interval regression by tolerance analysis approach[J]. Fuzzy sets and systems, 2012, 193: 85-107.

[11] Boukezzoula R, Galichet S, Bisserier A. A Midpoint-Radius approach to regression with interval data[J]. International Journal of Approximate Reasoning, 2011, 52(9): 1257-1271.

[12] Bargiela A, Pedrycz W, Nakashima T. Multiple regression with fuzzy data[J]. Fuzzy Sets and Systems, 2007, 158(19): 2169-2188.

[13] Billard L, Diday E. Regression analysis for interval-valued data[M]. Springer Berlin Heidelberg, 2000: 369-374.

[14] Billard L, Diday E. Symbolic regression analysis[M]. Springer Berlin Heidelberg, 2002: 281-288.

[15] Lima Neto EA, de Carvalho FAT. Constrained linear regression models for symbolic interval-valued variables[J]. Computational Statistics & Data Analysis, 2010, 54(2): 333-347.

[16] González-Rodríguez G, Blanco Á, Corral N, et al. Least squares estimation of linear regression models for convex compact random sets[J]. Advances in Data Analysis and Classification, 2007, 1(1): 67-81.

[17] Blanco-Fernández A, Corral N, González-Rodríguez G. Estimation of a flexible simple linear model for interval data based on set arithmetic[J]. Computational Statistics & Data Analysis, 2011, 55(9): 2568-2578.

[18] Hu C, He LT. An application of interval methods to stock market forecasting[J]. Reliable Computing, 2007, 13(5): 423-434.

[19] Chuang CC. Extended support vector interval regression networks for interval input-output data[J]. Information Sciences, 2008, 178(3): 871-891.

[20] 胡枫, 史宇鹏, 王其文. 中国的农民工汇款是利他的吗?——基于区间回归模型的分析[J]. 金融研究, 2008 (1): 175-190.

[21] 胡枫, 王其文. 中国农民工汇款的影响因素分析——一个区间回归模型的应用[J]. 统计研究, 2007, 24(10): 20-25.

[22] 李汶华, 郭均鹏. 区间型符号数据回归分析及其应用[J]. 管理科学学报, 2010, 13(004): 38-43.

[23] Chen LH, Lu HW. An approximate approach for ranking fuzzy numbers based on left and right dominance[J]. Computers & Mathematics with Applications, 2001, 41(12): 1589-1602.

[24] Bock HH, Diday E. Analysis of symbolic data: exploratory methods for extracting statistical information from complex data[M]. Springer, 2000.

[25] Hukuhara M. Intégration des applications measurables dont la valeur est un compact convexe[J]. Funkcialaj Ekvacioj, 1967, 10: 205-223.

[26] 吴育华,杜刚. 管理科学基础[M]. 天津：天津大学出版社, 2009.

[27] De Carvalho FDAT, De Souza RMCR, Chavent M, et al. Adaptive Hausdorff distances and dynamic clustering of symbolic interval data[J]. Pattern Recognition Letters, 2006, 27(3): 167-179.

[28] 方斌. 沪深300股指期货套利问题的实证研究[J]. 西安电子科技大学学报: 社会科学版, 2010，20(003): 78-85.

A Constrained CRM Regression Method for Interval Data

GUO Jun-peng, ZHAO Ru, LI Wen-hua

( College of Management and Economics, Tianjin University, Tianjin 300072, China)

Regression analysis is a statistical process for determining the relationships among variables. Traditional regression analysis takes point data as the research object. However, there are a large number of data which can’t be observed directly even though their variation intervals are available. For example, the stock index of a day is not a fixed data, because it always changes over time. A variety of methods to estimate the coefficients of interval regression models are studied in fuzzy theory, symbolic data analysis (SDA) as well as computer science. This paper also studies the estimation method for interval data.

Symbolic data analysis is a theory of extracting systematic knowledge from huge data sets. In the framework of SDA, many regression methods have been developed. The Centre method (CM) assumes that the lower and upper bounds of the interval have the same coefficients, and the coefficients can be obtained by minimizing the sum of the square of the lower and upper bound errors. The MinMax method (MinMax) assumes that the coefficients of the lower and upper bounds are different, and they can be estimated separately by applying the Least Square method. The Center and Range method (CRM) uses the mid-points and ranges of the intervals to represent the intervals. Two linear regression relationships are constructed with the center and radius series. The coefficients can be calculated using the Least Square method. CRM performs the best among all these methods. One of the shortcomings of CRM is that the predicted interval may be meaningless, because the predicted radius is less than zero sometimes. The Constrained Center and Ranger method (CCRM) is proposed to solve this problem. In the CCRM, all the coefficients of the radius relationship are non-negative, which can ensure the forecast radius being non-negative.

Another disadvantage of CRM is that it only fits the mid-points and the ranges of the intervals. In addition, it pays no attention to guarantee the prediction interval having overlaps with the sample interval. When the center series errors vary in a large range, there may be many predicted intervals which have no overlaps with the samples. The object of this paper is to solve this problem. A new constrained center and a range of methods are developed by adding some constrains to the CRM. The constraints ensure that the predicted intervals have some overlaps with the sample intervals. The constrained method can be expressed by a nonlinear programming. It is proved that the nonlinear programming is a convex programming. Thus, it can be solved through the K-T conditions. To evaluate the method, this paper studies the current main evaluating indicators. We summarize three kinds of measures, which are the Root Mean Square Error, the Coefficient of Determination and the Ratio. Some indicators are used in the paper, which are the root mean square error of the interval (), the average accuracy rate (), the average percentage of predicted intervals contained in the observed intervals (), as well as the average number of forecasts with 0% accuracy ().

Both Monte Carlo simulations and empirical analysis are used to evaluate our method. In the Monte Carlo simulation experiments, both simple regression (=1) and multivariate regression (=3) are considered. In each circumstance, three conditions are considered. The main difference of these conditions is the ranges of the errors. The results show that the larger the range of the errors, the better the new method performs in the measures,and. The results of simple regression are different from the results of multivariate regression. The linear relationship between CSI 300 and 50ETF is studied in the paper. The results indicate that the new method outperforms CRM in all the measures except the. In a word, The Monte Carlo simulations and the empirical analysis show that the constrained method performs better or the same in the aspects of,and. Sometimes the constrained method has better results than the CRM method in all the measures.

When there are some outliers in the samples, the new constrained method may not perform well. Thus, how to identify outliers and remove them are important research topics. Besides, how to achieve a balance between guaranteeing the overlaps and obtaining a loweris another topic worth studying.

regression analysis; interval; constraint; center and range method(CRM)

中文编辑：杜 健；英文编辑：Charlie C. Chen

O212.4

A

1004-6062(2016)04-0196-07

10.13587/j.cnki.jieem.2016.04.025

2013-07-12

2014-05-25

国家自然科学基金资助项目（71271147，71003072）；天津大学自主创新基金资助项目（2014XS-0024）

郭均鹏(1973—)，男，山东潍坊人；天津大学管理与经济学部教授，博士生导师，研究方向：管理科学，符号数据分析。