越库配送车辆调度问题的自适应遗传算法研究

缪朝炜，苏瑞泽，张 杰



越库配送车辆调度问题的自适应遗传算法研究

缪朝炜1，苏瑞泽1，张 杰2

（1. 厦门大学管理学院，福建厦门361005；2. 广东财经大学工商管理学院，广东广州510320）

本文研究的是带有车辆容量限制以及时间窗口约束的越库配送车辆调度问题，该问题旨在通过车辆与仓门的合理分配来实现越库内部货物的最优调度从而达到高效的运作目标。由于该问题是强NP难的问题，本文基于遗传算法的思想，设计了单点交叉算子和两点交叉算子，并采用“交叉行为自适应选择机制”设计了一种自适应遗传算法来进行求解。在数值实验中，本文将该自适应遗传算法与分别采用单种交叉算子的遗传算法进行算法性能的比较，通过大量不同规模的数值算例的结果对比发现在这三种算法中，采用自适应机制的遗传算法在最终解的质量上总体表现最好，表明该算法对于求解此类问题具有良好的性能，同时也表明该自适应机制对于提升算法性能上具有显著的促进作用。

遗传算法；自适应机制；越库；车辆调度

0 引言

在今天全球竞争日趋激烈的环境下，如何既能降低物流成本又能够保证货物的及时配送，这是许多企业都非常关注的问题。越库技术集库存管理策略与配送策略为一体，被各类企业应用于优化物流配送网络以达到降低库存水平，提高库存周转率，提升顾客服务水平的目的，如沃尔玛、Home Depot, Costco, Canadian Tire以及FedEx等企业都成功的实施了越库技术。现如今虽然越库的使用较为广泛，但对其还没有一个统一的定义。Gue[1]把越库当成是一种零担运输，只具备接发货物功能的转运中心。Napolitano[2]认为越库是一种几乎跨越仓储生命周期的运作策略，它通过设备将收到的货物和其他将运至同一地点的货物整合一起，尽可能快的运送给客户，不进行长期存储。对于越库的分类，之前文献已经提出了很多方法。如Yan和Tang[3,4]分别研究了前配送越库与后配送越库以及它们分别的适用环境。Shaffe[5]和Napolitano[2]根据产品所处的阶段，将越库分为制造型越库，分销型越库，零售型越库及机会型越库。另外，对于越库作业问题的研究范围较广，从战略层面到单个越库的运作层面，都有相关的研究成果，如：(1)越库的选址：Axsater[6,7]研究设施选址以及相关的越库策略（比如如何通过处理货物达到快速转运的目的）；(2)多越库的配送网络：Lim等人[8]研究了供应商和顾客带有时间窗口约束的越库运输网络模型；Miao等人[9]研究了带有时间窗口的多越库系统下固定路径车辆运输调度问题；(3)越库的布局：Bartholdi和Gue[10,11]研究了越库系统的最佳布局，并研究了特定布局下如何减少劳动力成本；(4)越库内部资源分配问题：Yu和Egbelu[12]研究了一个无库存容量限制的越库系统中如何调度进出车辆。Miao等人[13]考虑了类似于航空港中登机口分配的越库仓门分配问题，考虑了每一到达越库的车辆都被赋予一个服务的时间窗口，并给出了该问题的优化算法；(5)越库内部货物调度作业：Chen和Lee[14]提出一类需要找到一个最佳出入口车辆序列以使得总运作时间最少的越库调度模型，他们把该问题转化成经典的两台机器两个任务集的最小化最大完工时间问题，并给出多项式近似算法对该模型进行求解。由于目前不管是企业界还是学术界对越库方面的应用和研究都十分重视，越库方面相关的研究成果丰硕，因此在本文中不再一一赘述，有关越库方面的研究成果可以参阅Boysen和Fliedner[15]以及Jan 等人[16]的两篇关于越库研究的非常系统的文献综述。

本文研究了带有车辆容量限制以及时间窗口约束的越库配送车辆调度问题，该问题旨在通过车辆与仓门的合理分配来实现越库内部货物的最优调度从而达到高效的运作目标。与已有的文献不同的是，本文研究的问题不仅考虑了越库的容量限制，而且还考虑了车辆装载容量限制，而以往的研究往往只考虑前者甚至两者都不考虑，大大降低了研究该问题的实践意义，因为在实际越库运作中，车辆容量是非常重要的限制条件，对越库内部的优化调度以及运作绩效有着直接影响。对于此类越库运作问题，由于大部分都属于强NP难题，因此研究的重点在于如何设计高效的启发式算法来求解，如Miao 等人[13]针对考虑越库内部作业时间的车辆库门分配问题分别设计了GA和TS两种启发式算法。Vahdani和Zandieh[17]针对越库车辆调度问题的不同启发式算法的效果进行对比，并且利用数值实验证明每种启发式算法的稳健性。此外，陈峰和宋凯雷[18]、俞亮和陈峰[19]以及强瑞等人[20]也分别针对几种不同的越库物流以及车辆调度问题设计了高效的启发式算法进行求解。由于本文研究的越库车辆调度问题同样属于强NP难问题，因此基于遗传算法的思想，文中设计了单点交叉算子和两点交叉算子，并采用“交叉行为自适应选择机制”设计了一种自适应遗传算法来进行求解；最后通过大量不同规模的数值算例将该自适应遗传算法与分别采用单种交叉算子的遗传算法进行算法性能的比较，以此来分析不同算法的效率以及这种自适应机制的有效性。

1 问题描述与模型

本文研究的越库的常见结构如图1所示，该越库带有平行的两排库门，分别为货物的入库门与出库门，货物由入库车辆运送到越库，然后根据不同客户的需求，在操作区将货物进行重新分配，最后由出库车辆进行物流配送，在越库内部操作会引发相关的运作费用。实际问题中常会遇到由于库门资源以及车辆运输容量的制约，导致有些货物无法及时配送，这些货物将会短暂存储在越库中具有一定容量的临时存储区，此时将会带来额外的成本，比如仓储费用以及延迟发货成本等等，根据此类问题建模的常用方法，将其统一定义为惩罚成本。此外，实际操作中常会给每辆车辆分配特定的时间窗口，该做法可以有效的提高越库的利用率，但是也大大增加了实际工作的复杂性。本文采用的时间窗口由车辆的到达与离开时间来定义，要求每一辆入库（出库）车辆只能在给定的到达和离开时间内占用一个入（出）库门。同时，文中考虑了越库内转运、分拣、包装所需的越库内部操作总时间，并假设这个时间与入库门与出库门的相对位置有关，因为相对位置离的越远，则时间消耗越长，而且越库内部操作时间约束会影响内部调度转运方案的可行性，例如出库车辆A停靠在出库门a，要求配送停靠在入库门b的入库车辆B上面的部分货物，那么出库车辆A的离开时间必须晚于入库车辆B的到达时间和从入库门b到出库门a的越库内部操作总时间之和，这样入库车辆B才可能将货物装配到出库车辆A上，否则就会导致货延迟配送，同样会引发相应的惩罚成本。综上所述，在库门资源有限、车辆运载能力以及时间窗口限制等诸多实际限制条件下，研究如何合理的进行车辆库门分配以及货物调度，使得包括越库内部货物调度引发的运作成本以及由于延迟配送而引发的惩罚成本在内的总成本最小化问题是非常具有实践意义的。

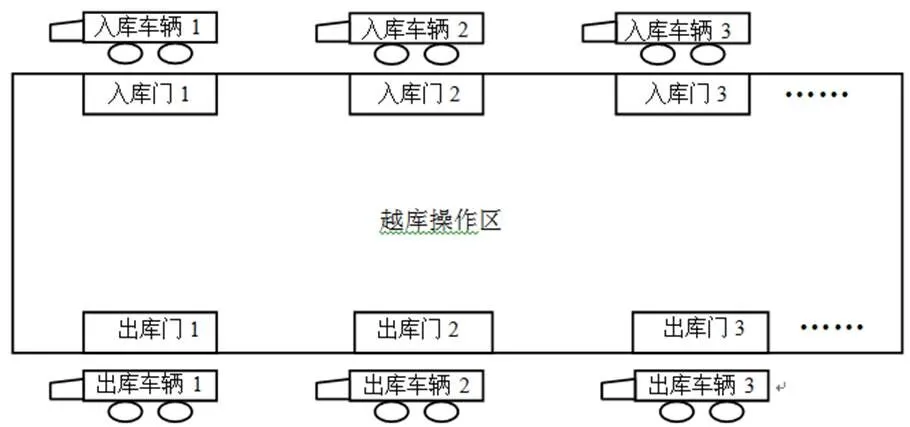
图1 越库结构

针对上述问题本文构建了0-1整数规划模型，首先介绍模型的参数符号如下：

决策变量定义如下：

目标是为了使总成本最小化，即运作成本与惩罚成本的总和最小。具体线性规划模型如下：

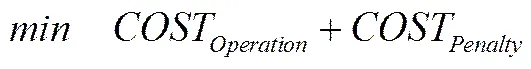
其中

(2)

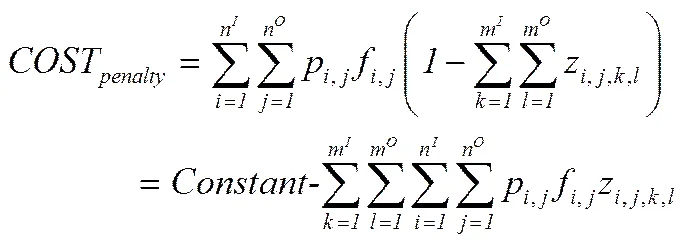
因此目标函数可以被改写成为下式：

(4)

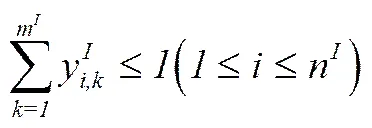
(6)

(7)

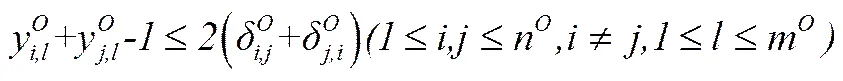
(9)

(10)

(12)

(13)

在上述模型中，约束条件（5）和（6）保证了每辆车至多只能分配一个库门；约束条件（7）和（8）表示每个库门在每一个时间点至多被一辆车占用；约束条件（9）给出了决策变量间内在的逻辑关系；约束条件（10）和（11）分别给出了出库车辆的运载容量限制以及越库临时存储区的容量限制条件；约束条件（12）给出了当车辆间货物转运可行时越库内部操作时间与车辆时间窗口之间需满足的条件；约束条件（13）给出了决策变量的取值范围。

2 自适应遗传算法设计

2.1 解结构设计

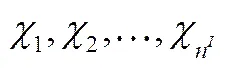
2.2 初始解生成

初始解对启发式算法的求解效果有很大的影响，质量高的初始解能够极大地提升搜索速度，因此在本文中，我们不采用随机产生初始解的方法，而是通过启发式策略分阶段产生初始解。由于入库车辆的入库门分配策略与出库车辆的出库门分配策略有着紧密的联系，因此在生成初始解时我们制定了以下5条规则：①先分配入库车辆的库门，后分配出库车辆的库门；②尽可能使每一辆车都能分配到库门；③尽可能较早的给所载货物总的惩罚成本较高的入库车辆分配库门；④尽可能降低批量大的货物的转运成本；⑤入库车辆库门分配完成后，尽可能先给所载货物总量较大的出库车辆分配库门。在给出具体初始解的生成步骤之前，先介绍相关参数如下：

：入库车辆；

：出库车辆；

：分配给入库车辆的入库门；

：分配给出库车辆的出库门；

此外，入库车辆库门优先选择概率和出库车辆库门优先选择概率分别由（14）和（15）式确定，从式(14)可以看出，入库车辆所载货物总的惩罚成本越高，其优先选择库门的概率越大。从式(15)可以看出，当入库车辆确定时，越大，相应的出库车辆的优先选择库门的概率越大。

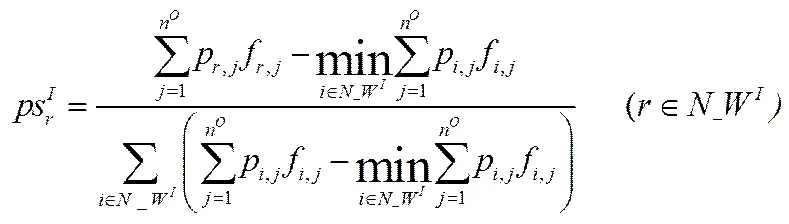
(15)

通过（14）和（15）式选定入库车辆和出库车辆以后，根据（16）和（17）式给出的概率确定入库门和出库门。

(17)

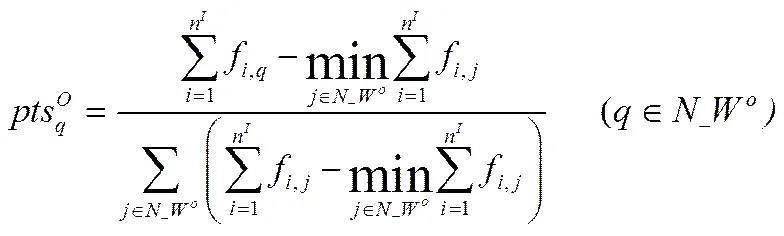
(19)

(20)

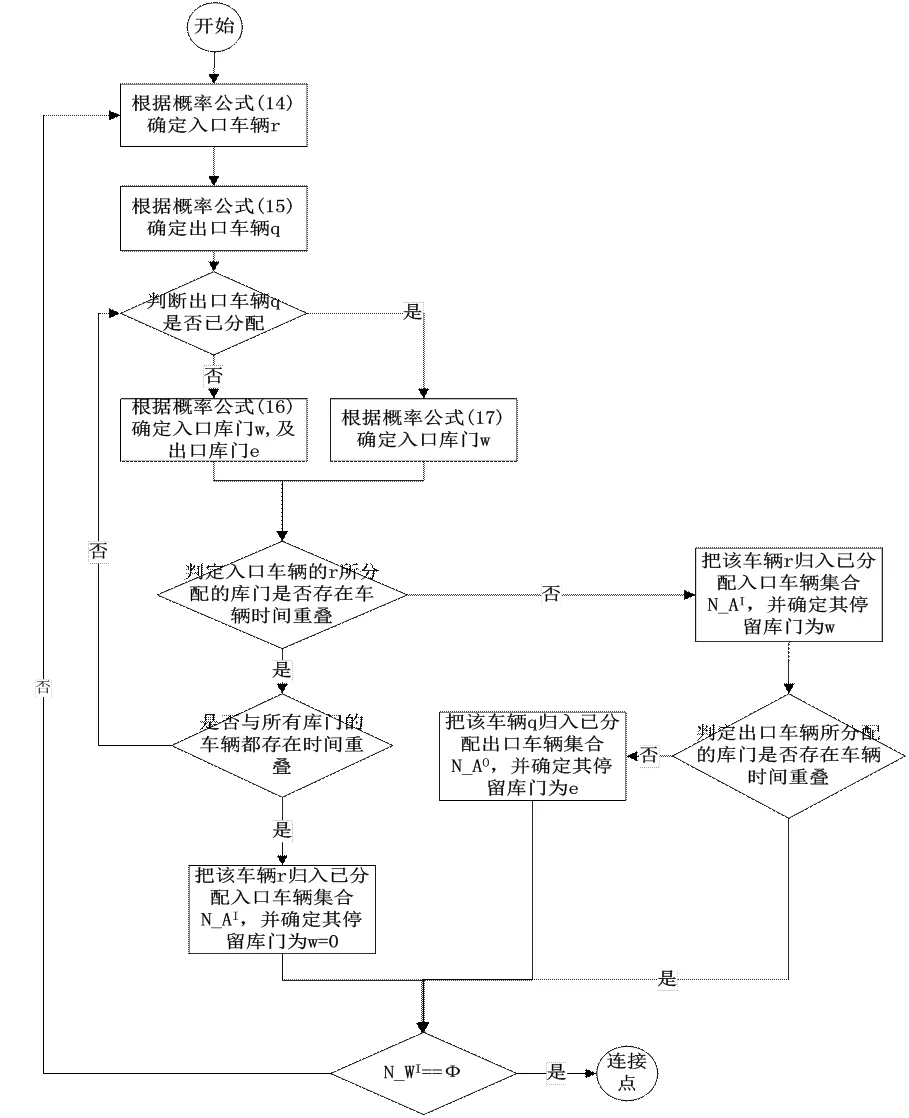
图1 入库车辆库门分配流程图

图2 出库车辆库门分配流程图

具体的入库车辆和出库车辆的库门分配流程如图2与图3所示。当库门分配结束后，还无法得到该问题的最终可行解，因为还必须制定内部货物的转运方案。基于贪婪算法的思想，采用单位价值贪婪策略，按的值对已分配库门的入库车辆的货物进行降序排列并依次分配给出库车辆，从而得到最终的可行解。

2.3 交叉算子

（1）单点交叉（SPCO）

单点交叉是遗传算法中最基本也是最常用的交叉算子，若个体基因位之间的联系较为紧密，并能提供较好的个体性状，那么单点交叉对个体模式的破坏较小，但其产生的新个体与父代的个体相似性较强，不易于维持种群的多样性。其步骤就是随机选取两个染色体作为父代，并随机生成一个交叉点，互换两个基因片段，形成两个新的个体[13]。具体如下所示，比如随机生成的交叉点是4。

随机选取两个染色体：

Parent1: X1 X2 X3 X4 X5 X6 X7 X8 X9

Parent2: Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9

生成新的个体：

Child1: Y1 Y2 Y3 Y4 X5 X6 X7 X8 X9

Child2: X1 X2 X3 X4 Y5 Y6 Y7 Y8 Y9

（2）两点交叉(DPCO)

两点交叉与单点交叉相比，在交叉过程中，所交叉的基因片段选择更大。其步骤是随机选取两个染色体作为父代，随机生成为两个交叉点，互换两个交叉点之点的基因片段，形成两个新的个体[20]。比如随机生成的交叉点是3和7，则

随机选取两个染色体：

Parent1: X1 X2 X3 X4 X5 X6 X7 X8 X9

Parent2: Y1 Y2 Y3 Y4 Y5 Y6 Y7 Y8 Y9

生成新的个体：

Child1: X1 X2 X3 Y4 Y5 Y6 X7 X8 X9

Child2: Y1 Y2 Y3 X4 X5 X6 Y7 Y8 Y9

但由于本文问题的特殊性，即分为入口车辆和出口车辆两部分，所以对两点交叉增加一个限制条件，即两个交叉点必须一个在入口车辆部分的基因段，而另一个必须在出口车辆的基因段。

2.4 变异算子

变异算子能为个体进化提供新的基因，使整个算法搜索能够探查到之前没有搜索的区域，是保持群体多样性、防止出现“早熟”的重要手段，是提高使算法跳出局部最优解的有效方法。

本文采用车辆的库门互换的变异方法[13, 20]，即对每个个体以给定的变异概率进行选取，然后对选中需要变异的个体，随机选取两个入（出）库门a和b，将分配给库门a的车辆分配给库门b，将原本分配给库门b的车辆分配给库门a。需要特别注意的是随机选取的库门必须是同一种库门，即都是入库门或者都是出库门，否则无法互换。

举个实例，假如交叉完后产生的新个体的入库门分配如下：

Child: 1 3 2 3 4 5 3 4 5

对其进行变异，假设随机选取的两入库门为3和4，那么对其他进行变异之后：

New Child: 1 4 2 4 3 5 4 3 5

采用该变异方法是考虑模型的特点，即对车辆进行库门分配时，受到车辆时间窗口的影响，采用库门互换的变异方法不但达到了变异的效果，而且可以保证变异后的新个体仍是可行解。

2.5 自适应机制

遗传算法中的各种算子的选择等对算法本身的效果影响很大，如交叉算子，虽然很多学者对单点交叉、多点交叉等算子的性能做了分析，但并不能有效的预测各种交叉算子使用的效果，因此Spears[21]认为采用自适应机制是最好的选择。本文采用的自适应机制属于对交叉行为的自适应选择，即采用何种交叉算子的选择。

单点交叉算子能够较好的保存父代的优良模式，但也因此降低了进化能力。两点交叉与单点交叉相比，在交叉过程中，所交叉的基因片段选择更大，对父代的基因结构破坏相对更大，但却可以提高寻找新优良模式的能力。因此可以考虑采用自适应机制，让算法自动选择交叉算子，尽可能的保留这两种交叉算子的优点。该自适应算子设计思路是根据单点交叉及两点交叉的特点，当交叉的父代个体适应度值大时，采用单点交叉的概率大；当交叉的父代个体适应度值小时采用两点交叉的概率大。因此本文结合神经网络中的神经元激活函数sigmoid函数[22]，采用一种反馈学习策略，如式(21)和(22)所示，其中、分别指每次采用两点交叉与单点交叉的概率；A取值9.903438；、、分别指群体中适应度的最大值、平均值以及当前个体的适应度值。对系数做多次实验，发现取值0.5的效果相对较好。

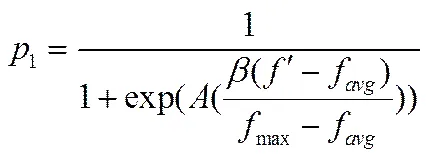
(22)

3 数值实验

本文通过随机生成数据的方法对不同规模的问题进行了大量的数值实验，主要目的是通过数值实验结果对比自适应遗传算法与分别采用单种交叉算子的遗传算法的性能，分析这三种算法的效率以及该自适应机制的有效性。实验在MS-Windows XP，Pentium 4 2.93GHz，1G内存的环境下测试。

3.1 数据生成与参数设定

数值实验中将算例分为三类，分别是小规模、中规模和大规模，算例的规模由入库车辆的数量、入库门的数量、出库车辆的数量以及出库门的数量来区分。入库车辆的服务时间窗口的开始时间，结束时间。对于出库车辆，，。库门与库门之间的运作时间是根据它们之间的相对距离来设置的，将正对的两个库门之间的运作时间设为2，相邻的库门之间运作时间设为1。运作成本，惩罚成本，车辆之间的需要运送的货物量，出口车辆的载重量限制，，越库临时库存容量限制，其中。遗传算法的参数设定如下：总的迭代次数104，最优解最大的重复代数100，种群规模400，每一代的交叉次数800，变异概率取0.1。

3.2 实验结果

数值实验分两个部分，首先验证本文设计的启发式策略分段产生初始解的方法相对于随机初始解生成方法的有效性，然后对比采用不同交叉算子的遗传算法的性能，以此验证自适应机制对提升算法性能的有效性。

为了验证本文设计的启发式初始解生成方法相对于随机初始解生成方法的有效性，本文按照车辆与仓门的不同数量选取了三个组合，每个组合含3个算例，每个算例分别采用上述两种初始解生成方法各产生1000个初始解，通过比较这些初始解的平均适应度值来分析两种方法的有效性。表1给出了具体的实验结果，虽然在问题规模很小的时候，随机生成初始解的方法的表现相对优于启发式方法，这主要是因为此时解空间小，随机生成方法有较大的概率选取到较优的初始解；然而随着问题规模的增大，解空间以几何级数扩大（这也是此类组合优化问题的一大特点），此时随机方法的劣势突显，而启发式方法由于采取了特定的选取规则，能够在众多的解中寻找到质量更好的初始解，对于此类组合优化问题具有良好的适用性，从数值实验结果也能够看出总体而言启发式方法优于随机方法。此外，在越库实践中，车辆和仓门的数量往往较多，问题规模也较大，因此启发式初始解生成方法在实践中也更加适用。

下面为了对比采用不同交叉算子的遗传算法的性能，生成三类不同规模的算例，每一类同样按照车辆与仓门的不同数量分成6组，每组各做10次随机实验。表2～表4给出了每组10次随机实验分别采用自适应机制、单点交叉以及两点交叉的遗传算法求解得到的平均实验结果，包括平均目标函数值以及平均求解时间（以秒为单位）。从表2～表4可以看出，对于不同规模的问题，算法的表现对比结果是一致的，都是自适应算法优于单点交叉，单点交叉优于两点交叉。因此，自适应遗传算法对于求解该问题是有效的，而且自适应机制对于提升算法性能有显著的效果。

表1 启发式初始解与随机法初始解的平均适应度值对比

表2 小规模问题数值实验结果

表3 中规模问题数值实验结果

表4 大规模问题数值实验结果

4 结论

本文研究了带有车辆容量限制以及时间窗口约束的越库配送车辆调度问题，该问题旨在通过车辆与库门的合理分配来实现越库内部货物的最优调度从而达到高效的运作目标。本文基于遗传算法的思想，采用了单点交叉算子和两点交叉算子的 “交叉行为自适应选择机制”设计了一种自适应遗传算法来进行求解。数值实验结果表明，采用自适应机制的遗传算法在最终解的质量上的表现要优于单独采用单点交叉算子或者两点交叉算子，说明自适应遗传算法对解决该问题的高效性，同时也表明该自适应机制对于提升遗传算法性能上具有显著的促进作用。

[1] Gue, K.R., The effect of trailer scheduling on the layout of freight terminals [J]. Transportation Science 1999, 33(4): 419–28.

[2] Napolitano, M., Making the move to cross docking-a practical guide [M]. Warehousing Education and Research Council, 2002.

[3] Yan, H., Tang, S. L., Pre-distribution and post-distribution crossdocking operations [J]. Transportation Research Part E, 2009, 45(6): 843-859.

[4] Yan, H., Tang, S. L., Pre-distribution vs. post-distribution crossdocking with transshipments [J]. Omega, 2010, 38(34):192-202.

[5] Shaffer, B.. Implementing the crossdocking operation [J]. IIE Transaction, 2000, 30(5):20-23.

[6] Axsater, S., New decision rule for lateral transshipments in inventory systems [J]. Management Science, 2003, 49(9):1168–1179.

[7] Axsater, S., Evaluation of unidirectional lateral transshipments and substitutions in inventory systems [J]. European Journal of Operational Research, 2003, 149(2):438–447.

[8] Lim, A., Miao, Z., Rodrigues, B., Xu, Z. Transshipment through crossdocks with inventory and time windows [J]. Naval Research Logistics Quarterly, 2005, 52 (8):724–733.

[9] Miao, Z.W., Yang, F., Fu, K., Transshipment service through crossdocks with both soft and hard time windows constraints [J]. Annals of Operations Research, 2012, 192: 21-47.

[10] Bartholdi, J.J., Gue, K.R., The Best Shape for a Crossdock [J]. Transportation Science, 2004, 38(2):235-224.

[11] Bartholdi, J.J., Gue, K.R., Reducing labor costs in an LTL crossdocking terminal [J]. Operation Rearch, 2000, 48(6):823-832.

[12] Yu, W., Egbelu, P.J., Scheduling of inbound and outbound trucks in cross docking systems with temporary storage. European Journal of Operational Research, 2008, 184(1):377–396.

[13] Miao, Z.W., Lim, A., Ma, H., Truck dock assignment problem with operational time constraint within crossdocks [J]. European Journal of Operational Research, 2009, 192(1): 105-115.

[14] Chen, F., Lee, C.Y., Minimizing the make span in two-machine crossdocking scheduling [J]. European Journal of Operations Research, 2009, 193(1):59-72.

[15] Boysen, N., Fliedner, M., Cross dock scheduling: Classification, literature review and research agenda [J]. Omega, 2010, 38(6):413-422.

[16] Jan, V.B., Paul, V., & Dirk, C., Cross-docking: State of the art [J], Omega, 2012, 40: 827-846.

[17] Vahdani, B., Zandieh, M., Scheduling trucks in cross-docking systems: Robust meta-heuristics [J]. Computers and Industrial Engineering, 2010, 58(1):12-24.

[18] 陈峰, 宋凯雷, 越库物流调度问题及其近似与精确算法 [J], 工业工程与管理, 2006, (6): 53-58.

[19] 俞亮, 陈峰, 最小化误工个数的越库调度模型与启发式算法 [J], 上海交通大学学报, 2009, (12): 1984-1988.

[20] 强瑞, 缪朝炜, 吴为民, 供应网络中越库转运中心仓门分配问题研究 [J], 管理工程学报，2011, (1): 209-215.

[21] Spears, W.M., Adapting crossover in evolutionary algorithms [C]. In: McDonnell, J.R., Reynolds, R.G., Fogel, D.B. (Eds.), Proceedings of the Fourth Annual Conference on Evolutionary Programming. MIT Press, Cambridge, MA, 1995: 367–384.

[22] 邝航宇, 金晶, 苏勇, 自适应遗传算法交叉变异算子的改进 [J]. 计算机工程与应用, 2006,42(12): 93-96.

An Adaptive Genetic Algorithm for the Truck Scheduling Problem in the Crossdock Distribution Center

MIAO Zhao-wei1, SU Rui-ze1, ZHANG Jie2

(1. School of Management, Xiamen University, Xiamen 361005, China;2. School of Business Administration, Guangdong University of Finance and Economics, Guangzhou 510320, China)

As a just-in-time (JIT) logistics technology, crossdock refers to the operation of pickup-delivery and order-dealt activities at any intermediate points between upstream suppliers and downstream customers. Those intermediate points include transshipment warehouse or distribution center. They are used to achieve the elimination of goods storage, which can be temporarily stored and generally not more than one or two days, and can greatly reduce response time and inventory cost as well. Crossdock is increasingly being used to optimize the distribution network of supply chain, which can significantly reduce company's inventory levels by integrating inventory management strategy and distribution strategy. Thus, crossdock can reduce not only inventory management cost and cargo loss rate, but also speed up cash flow. It is reported that many well-known multi-national companies, such as Wal-Mart, Unilever, Dell, and Cisco, have implemented this technique successfully. The truck scheduling strategy plays a very important role in operations within the crossdock distribution center, which has a significant impact on the operational efficiency of crossdock. A good truck scheduling strategy can increase operational efficiency, improve customer service level, and reduce the total cost.

Because crossdock-related problems are a hot topic in both academic and industrial areas nowadays, there is a lot of related research works in the previous literatures, which can be mainly divided into five categories: (1) the facility location problem of crossdocks; (2) the network flow problem in a multiple-crossdock distribution system; (3) the layout design problem within a crossdock; (4) the resource allocation problem within a crossdock; (5) the scheduling problem within a crossdock. In this paper, we try to extend the truck scheduling problem in a crossdock and consider the capacity constraint of outbound trucks as well as that of the crossdock. In reality, the number of inbound/outbound docks is limited, and the distance between inbound and outbound docks is different, and the amount of transshipment cargos and the time window for each inbound/outbound truck is different. Therefore, it is important to schedule these trucks to guarantee the number of trucks assigned to a door as many as possible so that cargos can be transshipped as many as possible and the transfer distance inside the crossdock can be minimum. These considerations will have a great impact on the efficiency and cost of crossdock operations. This paper tries to find a truck scheduling with a minimum cost under the time windows and capacity constraints of outbound truck and crossdock in order to increase the efficiency of crossdock operations.

In the first part, we introduce this truck scheduling problem including constraints, assumptions, notations as well as decision variables, by which we propose a 0-1 Integer Programming Model. This kind of optimization problem is NP-hard in the strong sense. As a result, we try to develop a genetic algorithm by adopting single-point crossover (SPCO) and double-point crossover (DPCO) adaptively to solve it.

In the second part, we introduce the steps of designing our adaptive genetic algorithm. We design the chromosome and adopt heuristic method to obtain a group of initial solutions at first rather than generate them randomly in order to obtain good quality ones because the quality of the initial solutions will influence the efficiency of the genetic algorithm greatly. SPCO and DPCO are developed as well as probability mutation operator. After that, an adaptive scheme is proposed to adopt the two crossover operators adaptively.

The third part is numerical experiments, where we compare the performance of the adaptive genetic algorithm with those adopting SPCO and DPCO, respectively. We not only show the generation procedure of those parameters, but also develop three categories experiments including large, medium and small scale instances respectively. The results show that the adaptive genetic algorithm has the best performance in terms of final near-optimal solution quality in all scenarios. These findings mean that the proposed adaptive genetic algorithm is a good way to solve this kind of truck scheduling problem. Moreover, it shows that this adaptive scheme can improve the efficiency of the genetic algorithm for this problem.

In summary, this paper tries to resolve the truck scheduling problem with the time windows and capacity constraints of outbound truck and crossdock, and develops an adaptive genetic algorithm to solve it. The numerical experiments show that our algorithm outperforms the others with a single crossover operator. This suggests that this adaptive genetic algorithm is an efficient way to solve this kind of problem.

genetic algorithm; adaptive scheme; crossdock; truck scheduling

中文编辑：杜 健；英文编辑：Charlie C. Chen

F224.3

A

1004-6062(2016)04-0166-07

10.13587/j.cnki.jieem.2016.04.021

2013-12-28

2014-05-26

国家自然科学基金资助项目（71371158，71301032）；教育部“新世纪优秀人才支持计划”资助项目（NCET-10-0712）；中央高校基本科研业务费资金资助项目（2012221011）。

缪朝炜（1980—），男，福建福州人；厦门大学管理学院教授，研究方向：物流与供应链管理。