平均跟踪的一些性质
2016-06-05刁素兰吴红英
刁素兰,吴红英
(1.广州大学数学与信息科学学院,广东广州510006;2.怀化学院数学与计算科学学院,湖南怀化418008)
刁素兰1,吴红英2
(1.广州大学数学与信息科学学院,广东广州510006;2.怀化学院数学与计算科学学院,湖南怀化418008)
研究了0.5-平均跟踪的一些性质.我们证明了:如果f是满射且有0.5-平均跟踪性质,则f是链传递的.如果f是等度连续满射且有0.5-平均跟踪性质,则f是拓扑遍历的.
跟踪性质;平均伪轨;拓扑遍历;链传递
1 引言与预备知识
设(X,f)是一个拓扑动力系统(简称动力系统),是指(X,ρ)是一个紧致度量空间,其中ρ表示X上的一个度量,f∶X→X是一个连续满射.跟踪性质在动力系统中扮演着重要的角色.1980年,Blank[1,2]引进了平均跟踪性质的概念并证明了某些摄动双曲系统具有平均跟踪性质.自从平均跟踪的概念问世以来,我们观察到两个现象.其一,平均跟踪性质受到了较多学者的关注[3-7].其二,越来越多新的跟踪概念出现[6,8-10].
设Z+是非负整数集.设A⊂Z+,用|A|表示集合A的基数.用d(A)表示集合A的上密度,用d(A)表示集合A的下密度,用d(A)表示集合A的密度.
设x0=x,x1,…,xn=y∈X,δ>0.对任意的i∈{0,1,…,n-1},如果ρ(f(xi),xi+1)δ,则称序列x0,x1,…,xn为映射f的从x到y长度为n的δ-链.称映射f是链传递的,是指对任意的两个点x,y∈X和任意的δ>0,都存在一条从x到y的δ-链.
设(X,f)是一个动力系统.U,V⊂X,记N(U,V)={i∈Z+∶U∩f-i(V)≠Ø}.称映射f是传递的,是指对任意两个非空开集U,V⊂X,有N(U,V)≠Ø.称映射f是拓扑遍历的,是指d(N(U,V))>0.



这时,也称点z,ε-平均跟踪ξ.
定义1.1设(X,f)是一个动力系统,q∈[0,1),称f具有平均跟踪性质,是指对任意的ε>0,存在δ>0,使得对f的每一条δ-平均伪轨,存在点z∈X,满足
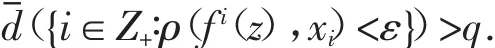

D.Ahmadi Dastjerdi在[8]引进了遍历伪轨的d-跟踪(d-跟踪)的概念.称映射f具有d-跟踪性质(d-跟踪性质),如果对任意的ε>0,存在δ>0,使得映射f的每一条δ-遍历伪轨都能够被X中的某点沿着下密度大于0(上密度大于0.5)的时间集ε-跟踪.
D.AhmadiDastjerdi在[8]中证明了:若映射f有d-跟踪性质(或d-跟踪性质),则f是链传递的.
称x∈X是f的一个稳定点,如果对任意的ε>0,存在δ>0,对每一个y∈B(x,δ)和每一个正整数n,有ρ(fn(x),fn(y))<ε.称f是Lyapunov稳定(或等度连续)的,如果X中每一个点都是稳定点.
称映射f是拓扑遍历的,如果任意两个非空开集U,V⊂X,N(U,V)有正上密度.文[12]证明了:如果f是一个Lyapunov稳定(等度连续)映射且有平均跟踪性质,则f是拓扑遍历的.
文[10]引进了平均伪轨的部分跟踪概念.称映射f具有q-平均跟踪性质,如果对任意的ε>0,存在δ>0,使得映射f的每一条δ-平均伪轨都能够被X中的某点沿着下密度大于q的时间集ε-跟踪.
本文将继续研究平均伪轨的部分跟踪性质.本文的主要结果为:如果f是满射且有0.5-平均跟踪性质,则f是链传递的(见定理2.2).如果f是等度连续满射且有0.5-平均跟踪性质,则f是拓扑遍历的(见定理2.3).
2 主要结果的证明
我们还需要下面的引理.
引理2.1设A,B⊂Z+,如果d(A)+d(B)>1,则d(A∩B)>0[9].
定理2.2设(X,f)是一个动力系统.如果映射f是满射且有0.5-平均跟踪性质,则f是链传递的.




定理2.3设(X,f)是一个动力系统.如果映射f∶X→X是一个等度连续的满射,并且具有0.5-平均跟踪性质,则f是拓扑遍历.
证明设U,V是X中的两个非空开集.我们选取x∈U,y∈V,取ε>0,满足B(x,ε)⊂U,B(y,ε)⊂V.由于f是等度连续的,则对上述ε>0,存在δ>0,使得当ρ(f(x,y)<δ时,对任意n∈Z+,有ρ(fn(x),fn(y))<ε.

定义序列如下:


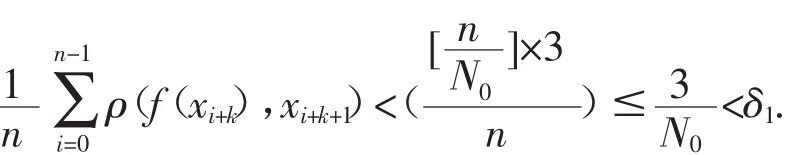
令

因此由引理2.1,d(J)x>0,d(J)y>0.选取i0∈JX,0≤k0≤N0-1,使得fi(0
z)∈B(f-k(0x),δ).对任意j∈Jy,且j≥i0+ k0,存在0≤mj≤N0-1,使得f(jz)∈B(f-m(jy),δ).由于f是等度连续的,因此有

注意到0≤mj≤N0-1,故d(N(U,V))>0,所以f是拓扑遍历的.
[1]M.L.Blank.Metric properties of-trajectories ofdynamical systems with stochastic behaviour[J].Ergodic Theory Dynam.Systems,1988(8):365-378.
[2]M.L.Blank.Deterministic properties of stochastically perturbed dynamical systems(Russian)[J].Teor.Veroyatnost.i Primenen.,1988,33(4):659-671.
[3]M.Kulczycki,D.Kwietniak and P.Oprocha.On almost specification and average shadowingProperties[J].Fund.Math,2014(224):241-278.
[4]D.Kwietniak,P.Oprocha.Anote on the average shadowingpropertyfor expansive maps[J].TopologyAppl,2012(159):19-27.
[5]Y.Niu.The average-shadowingpropertyand strongergodicity[J].J.Math.Anal.Appl,2011(376):528-534.
[6]P.Oprocha,D.A.Dastjerdi and M.Hosseini.On partial shadowingofcomplete pseudo-orbi-ts[J].J.Math.Anal.Appl,2013(404):47-56.
[7]J.Park,Y.Zhang.Average shadowingproperties on compact metric spaces[J].Commun.Korean Math.Soc.,2006(21):355-361.
[8]D.Ahmadi Dastjerdi,M.Hosseini.Sub-shadowings[J].Nonlinear Anal,2010(72):3759-3766.
[9]A.Fakhari,F.H.Ghane.On shadowing:ordinaryand ergodic[J].J.Math.Anal.Appl,2010(364):151-155.
[10]汪火云,曾鹏.平均伪轨的部分跟踪[J].中国科学,2016(3).
[11]R.Gu.On ergodictyofsystems with the asymptotic average shadowingproperty[J].Comput Math Appl,2008(550):1137-41.
[12]R.Gu.The average shadowingpropertyand topological ergodicity[J].J.Comput.Appl.Math,2007(206):796-800.
Some Properties of 0.5-average Shadowing
DIAO Su-lan1,WU Hong-ying2
(1.Department of Mathematics and Information Science,Guangzhou University,Guangzhou,Guangdong 510006;2.Department of Mathematics,Huaihua University,Huaihua,Hunan 418008)
In this paper,the authors studied some properties of the 0.5-average shadowing.We proved that if the map f is a surjection and has 0.5-average shadowing property,then it is chain transitive;If the map f is equicontinuous and has 0.5-average shadowing property,then it is topologically ergodic.
shadowing property;average pseudo-orbit;topologically ergodic;chain transitive
O189.11
A
1671-9743(2016)11-0018-03
2016-06-07
国家自然科学基金资助课题(11471125);广州大学数学与信息科学学科群重点学科建设项目.
刁素兰,1990年生,女,广东河源人,硕士研究生,研究方向:代数;吴红英,1974年生,女,湖南张家界人,副教授,研究方向:拓扑学与数值计算.
