基于特征提取的低信噪比拉曼光谱去噪方法研究

范贤光、王秀芬、王 昕*、许英杰、阙 靖、王小东、何 浩、李 韦、左 勇

1. 厦门大学航空航天学院、福建 厦门 361005 2. 北京长城计量测试技术研究所国防科技工业第一计量测试研究中心、北京 100095

基于特征提取的低信噪比拉曼光谱去噪方法研究

范贤光1、王秀芬1、王 昕1*、许英杰1、阙 靖1、王小东1、何 浩1、李 韦1、左 勇2

1. 厦门大学航空航天学院、福建 厦门 361005 2. 北京长城计量测试技术研究所国防科技工业第一计量测试研究中心、北京 100095

为了提高拉曼光谱检测系统的时间分辨率、常常需要采用较短的采样积分时间、此时带有分子结构振动谱的有用拉曼信号可能完全淹没在噪声中、严重影响信号的进一步分析、因此有必要对测量所得的光谱信号进行噪声消除处理。传统的消噪方法是基于信号与噪声在频域或统计特性之间的差异、通过平滑滤波或取平均值的方法来消除噪声、一般适用于噪声强度不高的情况、对于信噪比较低的情况处理效果并不理想。针对传统去噪方法的不足、从信号重构的角度、利用基于小波变换的谱峰识别、半峰宽检测提取光谱特征参数、再利用最小二乘拟合的方法、能够有效地提取淹没于强噪声背景下的有用拉曼信号。在仿真中、运用该算法得到的光谱曲线光滑、峰位置准确、信噪比改善明显。在实验中、分别利用该方法处理头孢呋辛酯片和罗红霉素拉曼光谱数据、得到了清晰的谱峰位置、幅值及半峰宽信息、实现了对短积分时间、强噪声背景的拉曼信号的有效还原、提高了检测系统的时间分辨率。仿真和实验结果表明、该方法需要调整参数少、易于实现、在信噪比比较低的情况下依然能够得到良好的去噪效果、为进一步分析光谱数据提供准确可靠的信息。

拉曼光谱； 去噪； 谱峰识别； 半峰宽

引 言

拉曼光谱(Raman spectroscopy)是一种基于拉曼散射效应的散射光谱[1]、由印度物理学家Raman发现。拉曼光谱技术具有非侵入、无损伤和无辐射等优点、是一种强有力的分析工具、正广泛地应用于生物领域的活体分析[2-3]、食品安全检测[4-5]、材料生产[6]和毒品快速检测[7]等领域。拉曼检测系统中的噪声主要由CCD散粒噪声、暗电流噪声、读出噪声等组成。在拉曼光谱的实际应用过程中、为了观察快速变化的动态过程、如观察肿瘤细胞的分裂过程等、需要采用较短的积分时间(如0.5 s)以提高光谱测量的时间分辨率。此时、获得的拉曼信号中、带有被测物质的指纹信息谱很容易淹没于强噪声背景下。因此、需要通过一定的方法对强噪声背景的拉曼光谱进行去噪处理、同时、也提高了检测系统的时间分辨率。

传统的拉曼光谱信号噪声消除方法有很多、如移动窗口平均平滑法、经验模态分解(empirical mode decomposition、EMD)等。这些算法都能在一定程度上实现拉曼光谱信号的噪声消除、然而也同样存在各自的问题。移动窗口平均平滑法、基于信号和噪声统计特性之间的差异、其基本假设是噪声为零均值噪声、通过对原始信号取平均值达到提高信噪比的目的、是消除噪声最常用方法。通过选择一个宽度为奇数2ω+1的平滑窗口、以中心波长点k为参照点从左到右移动窗口、将窗体覆盖区域内所有测量的平均值代替中心波长点对应的测量值、直至完成所有点的平滑、该方法平滑窗口宽度ω影响平滑结果、宽度太小、平滑效果不佳、宽度太大、则平滑掉特征峰信息、造成光谱失真； 且存在边界问题。对于宽度为数2ω+1的平滑窗口、光谱左右两端各有ω个点不能被处理。

EMD将信号分解成有限个由高到低、时间尺度由小到大的本征模态函数(instrinsic mode function,IMF)分量及单一趋势项、缺少严格的数学根据、更多的是一种基于经验的判断、且停止准则难以确定、同时存在端点效应、模态混叠效应、算法稳定性并不高。

传统消噪方法适用于噪声强度不高的情况、对淹没于强噪声背景下的拉曼信号效果不佳。因此、本文提出一种基于特征提取的光谱去噪方法。首先、通过对原始拉曼信号进行小波变换、搜索脊线进行谱峰位置和强度检测、然后基于信号与噪声在不同分解尺度的不同形态获取半峰宽、最后根据获得的峰值和半峰宽进行最小二乘拟合、从而实现强噪声背景下的拉曼信号信噪分离。

1 理 论

1.1 基于脊线提取的谱峰识别

采用连续Mexian Hat小波变换进行谱峰识别、该小波定义如式(1)所示。

(1)

对拉曼信号f(x)做连续Mexian Hat小波变换有

=f(x)*φa(b)

(2)

其中、a为伸缩因子、b为平移因子、φ*表示φ的共轭。Wf(a，b)正比于f(x)与标准差为a的高斯概率密度函数卷积的二阶导。由于拉曼光谱近似为高斯函数形式、其二阶导数在谱峰位置必然表现为局部极大值。同一谱峰在不同尺度上的局部极大值位置相近、该局部最大值随小波尺度变大而变大、且当尺度与峰的大小接近的时候达到最大、如图1所示、小波系数的三维图呈现山脊的形状、搜索出小波系数矩阵中的脊线即可识别出谱峰[8-9]。

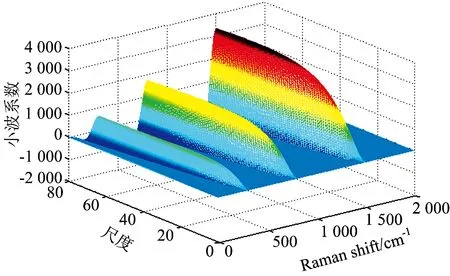
图1 CWT系数的脊线图

小波脊线的提取有两种最基本的方法、即基于小波系数的模极大值或相位信息的提取方法[10]。理论上讲、以小波变换的相位变换涉及到相位求导、噪声非常敏感、只有在比较高信噪比下才能准确提取信号小波变换的脊线。因此本文根据模值信息提取小波脊线Carmona方法、通过有小尺寸的极大值向大尺寸蔓延的方式进行脊线搜索。在获得脊线中选取顺利连接到最大尺度的脊线、运用阈值法剔除由于噪声引起的强度较弱的部分、留下的部分的最大尺度点即为识别的峰值点。由于噪声强度大、在提取的谱峰中可能存在由噪声引起的“假峰”、由于噪声的零均值随机性、故采用参照平均信号的方式剔除部分假峰。

另外、对信号进行小波变换时、要求信号是无限长的、对于有限长信号、存在一个边界延拓问题[11]。基线产生两端干扰峰、因此采用边界元素复制法、延拓两端的信号长度。

1.2 半峰宽检测

半峰宽是指峰高一半处的宽度、峰宽则代表谱峰两侧观测拐点处所做的两条切线与基线的两交点之间的距离。目前、主要采用以Harr小波为母函数的连续小波变换求导的方法进行峰宽检测、但是理论上讲、该方法得到的既不是峰宽也不是半峰宽、而是一个与谱峰相近的宽度。另外、对积分时间短、信噪低的拉曼信号进行哈尔小波变换、得到的波形平滑度很差、因此峰宽检测误差也很大。

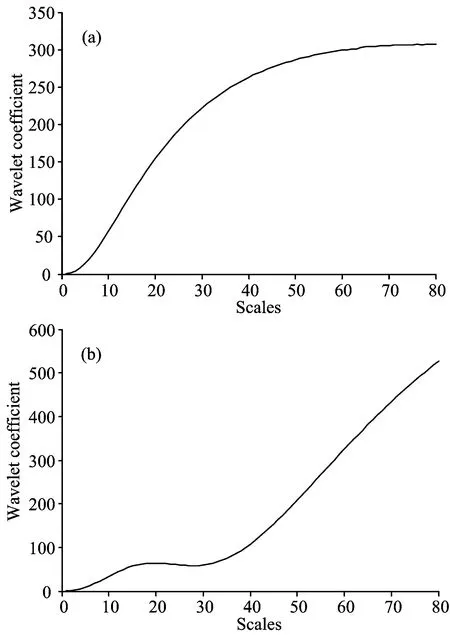
图2 不同尺度下、单峰(a)和重叠峰(b)的小波系数

本文采用文献[12]所述的方法求取半峰宽。图2(a)和(b)分别为单峰处和重叠峰处小波变换局部极大值随尺度变化的曲线。对于单峰、当尺度较小时、局部极大值随着尺度的增加而较快的增大、直到尺度与谱峰宽度相匹配、由于受到基线的影响、局部极大值随尺度的变化趋于平缓、利用这点我们可以估计单峰的谱峰宽度[12]。对于重叠峰、当尺度增大到一定程度时、由于受到相邻谱峰的影响、小波系数会呈现下降趋势、为了避开基线及相邻峰对峰位的干扰、我们找到峰位置处的全部尺度的极大值、选取符合要求的第一个或第二个极大值作为半峰宽。

1.3 基于最小二乘的信号重构

最小二乘法是一种由观测数据估算线性模型中未知参数的方法,其基本思想是选择估算量使得模型输出与实际测量输出之差的平方和达到最小、能有效避免正负误差相抵、且数学处理方便。

基于谱峰的位置、强度和半峰宽信息、利用最小二乘法对原始拉曼信号进行重构。首先、单个拉曼峰可近似为高斯峰[13-14]、即

(3)

式中、γG为高斯峰的半宽、w为峰位置、v为拉曼位移。

考虑拉曼光谱本身的荧光背景、拉曼光谱可以表示为N个高斯峰G(v，[γGi，wi])(i=1,2,…,N)、基线B(v)及拟合残差的累积形式r(v)、即

(4)

其中、ai为拉曼谱峰拟合系数、φB为基线拟合系数。

具体拟合步骤如下：

(1) 根据峰值检测和峰宽检测步骤确定的峰值点个数m、确定拉曼峰高斯拟合函数个数N=m；

(2) 根据谱峰识别获取的峰位置Peak[i](i=1,2,…,N)和半峰宽检测获得的各峰的半宽Halfwidth[i](i=1,2,…,N)、按照式(4)创建光谱曲线拟合表达式。其中、采用二次多项式B(v)=b0+b1v+b2v2拟合拉曼光谱的基线。

(3) 构造正规方程组、求解各项系数a1、a2、…、aN、b0、b1、b2、即得重构的拉曼光谱表达式。

2 仿 真

根据光谱硬建模理论及拉曼谱峰近似高斯峰的假设[15]、采用高斯函数簇的线性组合逼近实际拉曼光谱曲线、构建的仿真拉曼光谱曲线如图3(a)所示、峰位置、峰幅值及半峰宽参数见表1所示。对仿真信号加上强度为60 dB噪声后的信号如图3(b)所示。采用本文算法对上述加噪信号进行处理、峰值检测小波分解尺度为scales=1∶32、捕捉到的峰位置为Peak=[300,802,1 499]、半峰宽检测中获取的半峰宽Halfwidth=[13,5,13]。图3(c)中实线部分为算法处理后的信号、虚线为仿真理想信号、作为评价算法性能的参考信号。

表1 仿真信号参数表

如图3(c)所示、采用本算法处理的信号与理想仿真信号基本上重合、谱线平滑、识别的谱峰位置准确、基本保留了信号的谱峰强度、且峰形合理。

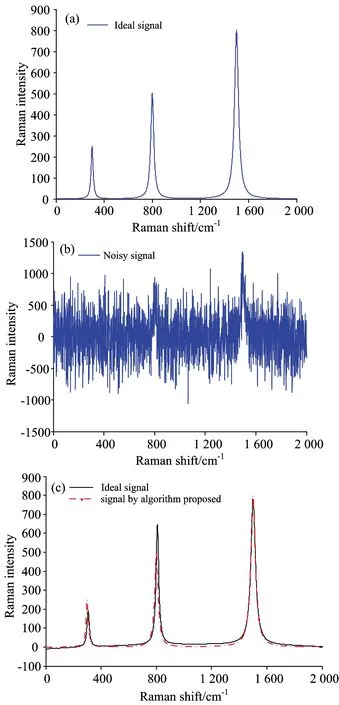
图3 仿真信号(a)、噪声信号(b)和仿真信号与去噪信号比较图(c)

Fig.3 Ideal simulation signal (a),noisy signal (b)and Comparison between ideal signal and signal by algorithm proposed (c)

采用信噪比(SNR)和均方误差(MSE)评价算法性能、信噪比和均方误差定义如式(5)和式(6)所示。

(6)

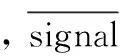
表2 处理前后信号的SNR和MSE

3 实验部分

3.1 材料及仪器

本文采用nanophoton公司开发的第三代拉曼成像系统拉曼-11分别测量头孢呋辛酯片(积分时间0.2 s)和罗红霉素(积分时间1 s)。

3.2 结果分析

利用本文算法分别对头孢呋辛酯片(cefuroxime axetil tablets,CA)和罗红霉素(roxithromycin、RC)的拉曼光谱进行处理。

图4(a)为头孢呋辛酯片(积分时间为0.2 s)的原始测量信号、图4(b)为采用本文算法重构出的去噪信号。其中、峰值检测算法中、小波变换尺度为scales=1∶32、得到的峰值点为PeakCA=[71,335,487,604]、HalfwidthCA=[7,6,14,15]。

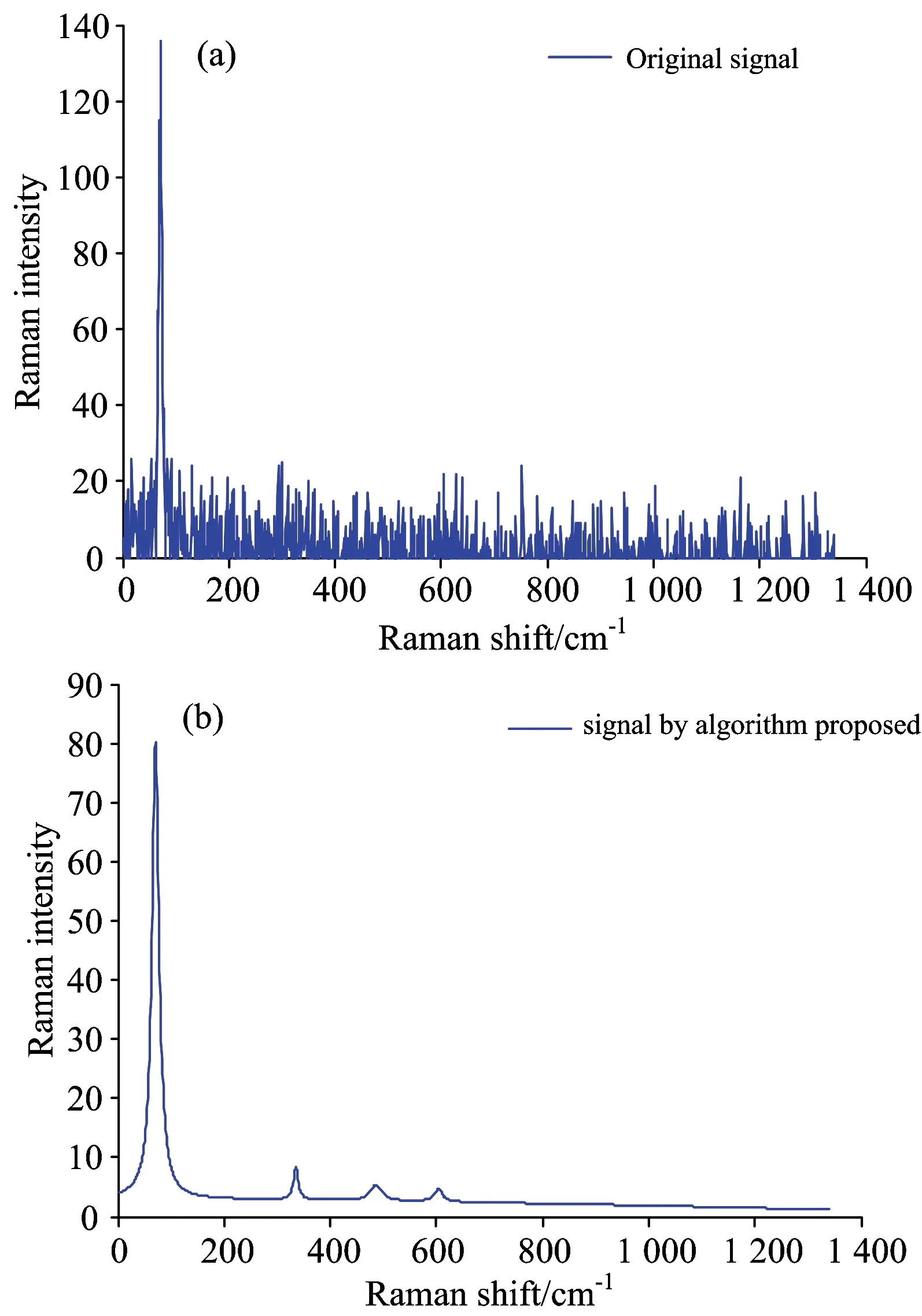
图4 头孢辛酯片原始拉曼信号(积分时间：0.2 s、a)和本文处理后的信号(b)

Fig.4 Original Raman signal of Cefuroxime Axetil Tablets with 0.2 s integration time(a)and signal by algorithm proposed(b)

图5(a)为罗红霉素(积分时间为1 s)的原始测量信号、图5(b)为采用本文算法重构出的去噪信号信号。其中、峰值检测算法中、小波变换尺度为scales=1∶16、得到的峰值点分别为: PeakRC=[52,104,181,529]、HalfwidthRC=[14,13,8,8]。

由图4(a)、图5(a)可以看出、带有被测物质头孢呋辛酯片和罗红霉素指纹谱峰信息已经完全淹没在噪声背景中、我们无法从原始测量拉曼光谱中提取出可供进一步分析的有用信息。由图4(b)、图5(b)可知、采用本文算法重构的光谱信号峰形合理、谱线光滑、峰位置、幅值及半峰宽信息清晰、实现了对短积分时间、强背景噪声拉曼信号的还原、提高了检测系统的时间分辨率。

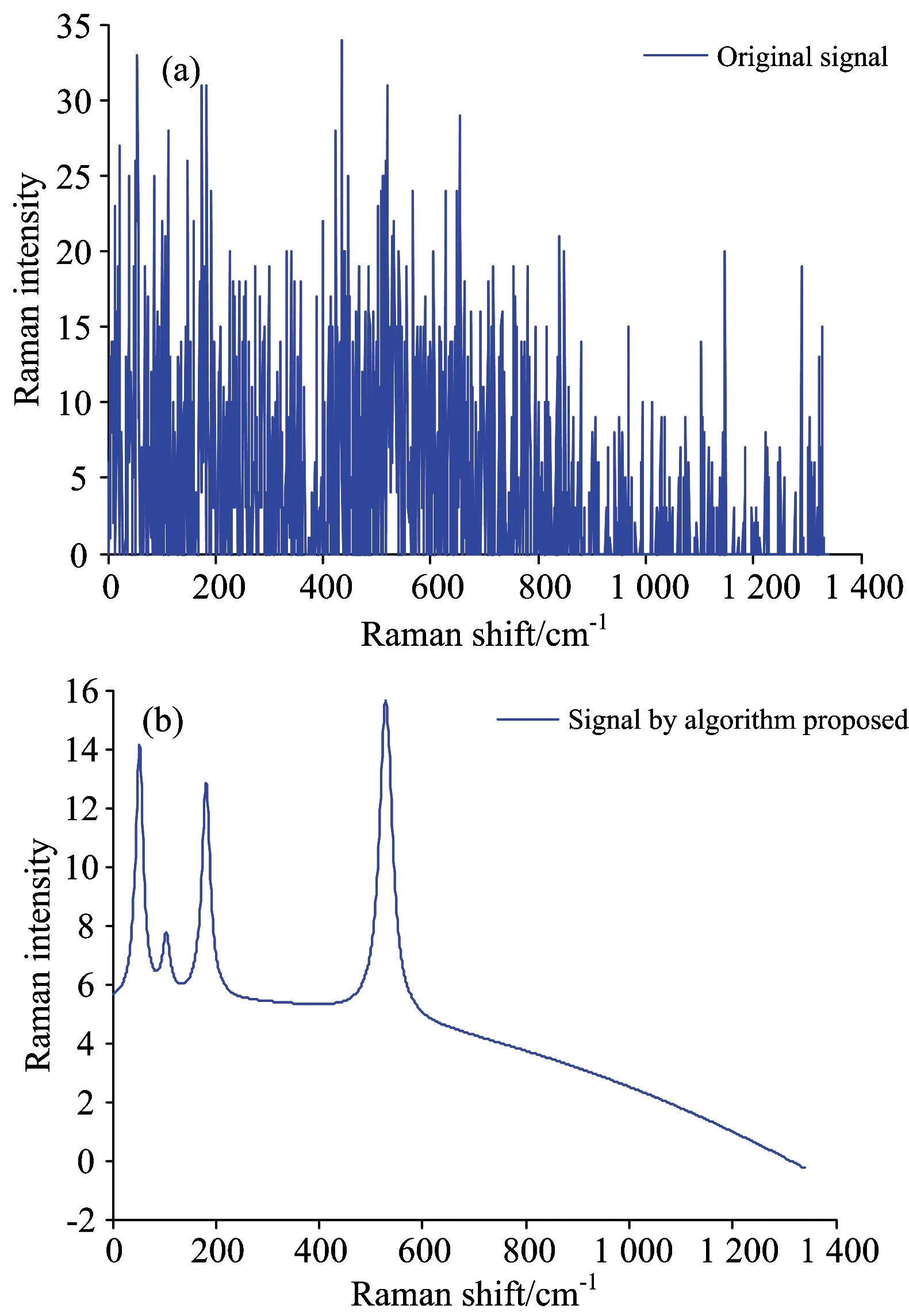
图5 罗红霉素原始拉曼信号(积分时间：1 s、a)和本文处理后的信号(b)

Fig.5 Original Raman signal of Roxithromycin with 1 s integration time (a) and signal by algorithm proposed (b)

为了比较本文方法与传统去噪方法、利用移动窗体平均平滑法处理图4(a)所示的头孢呋辛酯片信号和图5(a)所示的罗红霉素信号、结果如图6所示。移动窗体平均平滑法的窗体宽度对平滑效果影响很大、且没有相应的准则指导选取。经过多次试验、移动窗体平均平滑法采用的窗体宽度为15时平滑效果相对较好。由图6可以看出经过移动窗体平均平滑法处理后的信号仍存在明显的尖峰噪声、信噪比低、带有被测物质分子振动的谱峰信息仍旧无法直观获取、而采用本文算法处理的信号谱线平滑、信噪比改善明显、谱峰信息直观清晰。

综上所述、通过对原始信号取平均值的方法提高信噪比的传统去噪方法对于背景噪声强、信噪比低的拉曼信号去噪效果并不理想、处理得到的光谱曲线仍旧存在明显的噪声，

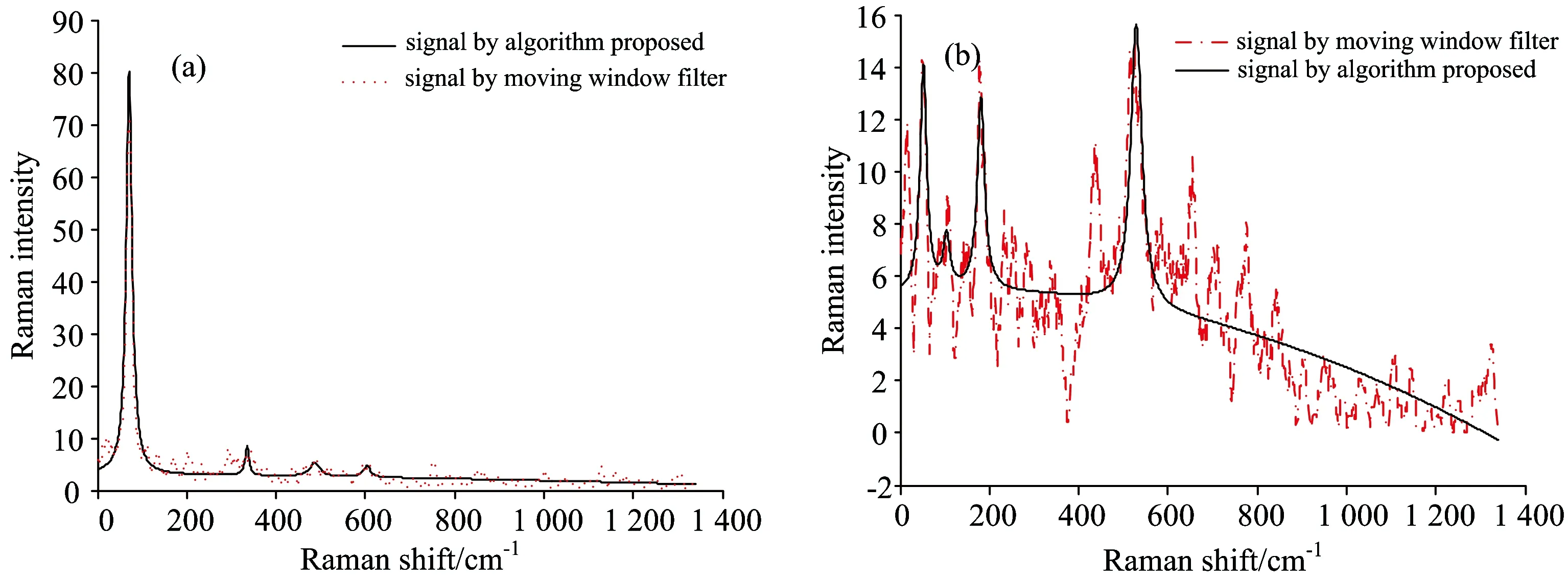
图6 算法处理结果对比(本文算法和移动窗口滤波)、头孢辛酯片(a)和罗红霉素(b)

信噪比改善不大、仍旧无法提取出被测物质的有效信息。而本文提出的基于特征提取的信号重构方法、能够对被强噪声背景淹没的信号实现有效的噪声消除、获取的拉曼光谱曲线平滑、信噪比改善明显、峰位置定位准确、谱峰强度也得到了很好的保留。

4 结 论

提出了一种基于特征提取和信号重构的强噪声背景下的拉曼光谱噪声去除方法。该算法先利用连续Mexian Hat小波变换进行谱峰识别、然后根据峰位置附近小波变换系数随尺度变化规律、提取拉曼谱峰半峰宽、最后根据获取的峰位置和半峰宽、采用高斯函数作为拟合函数、利用最小二乘拟合进行光谱重构、实现了强噪声背景下的拉曼光谱信噪分离、能够有效地提取淹没于强噪声背景下的拉曼信号。与传统的基于噪声去除方法相比、本文提出的算法能够在信噪比较低情况下、有效地重构出被强背景噪声淹没的拉曼信号、大大提高了检测系统的时间分辨率。此外、本文提出的算法调整参数少、易于实现、能够很好地与现有的拉曼仪器软件相结合。

[1] WEI Na,FENG Xu-qiao,ZHANG Xiao-fang,et al(韦 娜,冯叙桥,张孝芳、等). Spectroscopy and Spectral Analysis(光谱学与光谱分析),2013,33(3): 694.

[2] Keng H C,Hiro-o H、Shinsuke S. The Royal Society of Chemistry,2011,47(33): 9423.

[3] NIU Li-yuan,LIN Man-man,LI Xue,et al(牛丽媛,林漫漫,李 雪、等). Laser & Optoelectronics Progress(激光与光电子学进展),2012,49(6): 063001.

[4] Jagtiani A V,Sawant R,Carletta J. Measurement Science and Technology,2008,19(6): 1.

[5] Ismail H B,Havva T T,Hüseyin E G,et al. Royal Society of Chemsitry,2015,5: 56606.

[6] WU Juan-xia,XU Hua,ZHANG Jin(吴娟霞,徐 华,张 锦). Acta Chimica Sinica(化学学报),2014,72(3): 301.

[7] WANG Lei,GUO Shu-xia,DAI Yin-zhen,et al(王 磊,郭淑霞,戴吟臻、等). Chinese Journal of Analytical Chemistry(分析化学研究学报),2015,43(1): 33.

[8] Du P,Kibbe W A,Lin S M. Bioinformatics,2006,22(17): 2059.

[9] JIANG Yong-hua,MO Xiao-qiang,YOU Jia-yi,et al(蒋永华,莫小强,尤佳伊). China Measurement &Test(中国测试),2013,39(3).

[10] CHEN Yun-gu,SU Ben-yue(陈蕴谷,苏本跃). Chinese Journal of Quantum Electronics(量子电子学报),2012,29(6): 665.

[11] FENG Lin,JING Yi-chen,MEI Lin-li. Journal of Propulsion and Power(推进与动力杂志),2004,20(2): 319.

[12] DENG Xian-lai,JI Guo-yi(邓先来,纪国宜). Noise and Vibration Control(噪声与振动控制),2012,3: 72.

[13] JIANG Cheng-zhi,SUN Qiang,LIU Ying,et al(姜承志,孙 强,刘 英、等). Acta Optica Sinca(光学学报),2014,34(6): 299.

[14] LI Jin-rong,DAI Lian-kui,RUAN Hua(李津蓉,戴连奎,阮 华). CIESC Journal(化工学报),2012,63(7): 2128.

[15] LI Jin-rong,DAI Lian-kui,WU Xiao-li(李津蓉,戴连奎,武晓莉). Chinese Journal of Analytical Chemistry(分析化学),2014,42(10): 1518.

*Corresponding author

Research of the Raman Signal De-Noising Method Based on Feature Extraction

FAN Xian-guang1、WANG Xiu-fen1、WANG Xin1*、XU Ying-jie1、QUE Jing1、WANG Xiao-dong1、HE Hao1、LI Wei1，ZUO Yong2

1. School of Aerospace Engineering,Xiamen University,Xiamen 361005,China 2. Changcheng Institute of Metrology & Measurement,The 1st Metrology &Measurement Research Centre of National Defense Science Industry of China,Beijing 100095,China

To improve time resolution of the Raman measurement system,we need to adopt short scanning time. In this case,the weak Raman signal with vibrational spectrum of the molecular structure is easily to be buried by the high background noise,which influences the further analysis seriously. So it is necessary to de-noise the raw Raman signals. Conventional methods manage to de-noise signal by means of smoothing or averaging based on the difference between signal and noise in frequency characteristic or statistical features. They are commonly applied in the situation where the background noise is not so strong,and cannot give satisfactory results to the Raman signals with low signal-to-noise ratio. In this paper,the algorithm proposed detects peak positions and get peak half-width based on wavelet transform,and then reconstructs the Raman signals by least square fitting algorithm with characteristic parameters obtained,which extracts the useful signal from high background noise efficiently. In the simulation,the Raman curve fitted by the proposed algorithm was smooth,and the peak positions obtained were accurate,so the signal-to-noise ratio improved significantly. In the experiment,we adopted this algorithm to de-noise the tested Raman signal of Cefuroxime Axetil Tablets and Roxithromycin,respectively. The peak positions,peak half-width and amplitude were obtained and proved to be accurate. Therefore,the useful pure Raman signal could be recovered from the high background noise efficiently by the proposed algorithm,which improved the time resolution of Raman system. Both the simulation and the experiment showed that the proposed method could be easily performed with only a few parameters. Comparing with conventional methods,it could achieve satisfactory results under high background noise and provide accurate and reliable information for further analysis.

Raman spectroscopy; De-noise; Peak detection; Peak half-width

Aug. 31,2015; accepted Dec. 11,2015)

2015-08-31、

2015-12-11

国家自然科学基金项目(21503171)、中央高校基本科研业务费项目(20720150091、20720150094)、福建省高端装备制造协同创新中心资金项目资助

范贤光、1980年生、厦门大学航天航空学院仪器与电器系副教授 e-mail: fanxg@xmu.edu.cn *通讯联系人 e-mail: xinwang@xmu.edu.cn

TH744.1

A

10.3964/j.issn.1000-0593(2016)12-4082-06