基于Monte Carlo法对厚大矿体首采采场生产能力的验证
2016-06-05任青云云南延发矿业科技有限公司云南昆明65000湖南有色金属研究院湖南长沙4000
刘 彬,任青云(.云南延发矿业科技有限公司,云南昆明 65000;.湖南有色金属研究院,湖南长沙 4000)
基于Monte Carlo法对厚大矿体首采采场生产能力的验证
刘 彬1,任青云2
(1.云南延发矿业科技有限公司,云南昆明 650200;2.湖南有色金属研究院,湖南长沙 410100)
根据黑龙江某钼铅锌矿可行性研究报告,对该矿的首采采场进行生产能力的验证。运用蒙特卡罗法对该矿生产能力进行验证,主要包括可布置的矿块数量和新中段准备时间。结果表明,蒙特卡罗法在分析可信度验证有很好的优势,且验证结果与可行性报告结果相一致。
Monte Carlo;首采采场;生产能力验证
根据大兴安岭地区某钼铅锌矿床开采生产进度计划,计划2015年投产,年生产能力达到300万t,2016年年生产能力递增到500万t,2017年上部系统达产,年生产能力达到750万t。根据主要开拓系统和辅助开拓系统的掘进速度,上述生产能力的实现只能依靠上部系统开采来实现。而根据该矿的《可行性研究报告》,设计上部年生产能力为100万t,为此,需对上部系统首采区方案开展课题研究,以满足该矿床开采生产进度计划的要求。
据可研报告,上部系统采用上行式开采,首采中段为224~284 m,集中运输水平为200 m,采用中深孔分段落矿嗣后充填采矿法开采。而根据上部系统主要开拓井巷的掘进速度,在2015年前,无法形成这种开拓系统,且该上部系统首采区方案无法满足该钼铅锌矿床开采生产进度计划的要求。邓秉德[1]等人应用蒙特卡罗方法分析洪涝灾害的危险性。蒙特卡罗法对测量的不确定度的评定已经有大量的研究[2~6]。因此,基于蒙特卡罗法对不确定性因素的广泛应用,本文结合实际情况应用蒙特卡罗法对其首采采场的生产能力进行可信度验证。
1 Monte Carlo原理
蒙特卡罗法[7](Monte Carlomethod)是以概率和统计的理论、方法为基础的一种计算方法,将所求解的问题同一定的概率模型相联系,用电子计算机实现统计模拟或抽样,以获得问题的近似解,故又称统计模拟法或统计试验法。Monte Carlo方法的实质是通过大量随机试验,利用概率论解决问题的一种数值方法,基本思想是基于概率和体积间的相似性。Monte Carlo在计算的中间过程中出现的数是随机的,但是它要解决的问题的结果却是确定的。
Monte Carlo的基本思想是:当所求解问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。
在解决实际问题的时候应用Monte Carlo主要有两部分工作,首先用Monte Carlo模拟某一过程时,需要产生各种概率分布的随机变量;最后用统计方法把模型的数字特征估计出来,从而得到实际问题的数值解。
将Monte Carlo分为三个步骤:
1.依据概率分布ψ(x)不断生成随机数x,并计算f(x)。由于随机数性质,每次生成的x的值都是不确定的,为区分起见,可以给生成的x赋予下标。如xi表示生成的第i个x。生成了多少个x,就可以计算出多少个f(x)的值。
2.将这些f(x)的值与期望的值y进行比较,如果f(x)>y,则结果n加1(开始n=0)。
3.到达停止条件后退出。常用的停止条件是设定最多生成N个x,数量达到后即退出。
2 首采中段生产能力可信度验证
矿山生产能力,是指矿山企业在正常时期可能达到的单位时间(年或日)内生产的产品数量。一般用年产量表示,也有用日产量表示的。
在确定矿山生产能力时要考虑的主要因素有:(1)矿床开采自然条件:储量、品位、矿床产状及分布等;(2)国民经济对该种矿产原料的需求情况;(3)矿区开采技术经济条件:投资,水、电、设备供应,外部运输等。
最后确定的矿山生产能力应该在以上几个条件同时允许的范围内。按技术可能性确定生产能力的方法有两种:按可布矿块数和按新水平准备。将首采区选在350 m,对首采区生产能力可信度进行验证。
2.1 按可布矿块数的生产能力验证
2.1.1 基于不确定理论的计算公式
首采区段选在350 m,各主要回采工艺不同时进行考虑,同时回采矿块数确定生产能力按式(1)计算:

式中:A为矿山中段年生产能力/t·a-1;N为生产中段可布的矿块总数,取40~70个;k为矿块利用系数,取0.10~0.25;q为矿块生产能力,取0.2×104~0.4×104t/d;z为副产矿石率,取5%~20%;E为地质影响系数,取0.8~1.0;t为年工作日,t=330 d。
首采中段矿块布置如图1所示,可布置的块矿数经计算大致范围为40~70块;由于采用大直径深孔嗣后充填采矿法,且矿山矿块布置得比较密集,矿块的利用系数比较低,参考相似大型金属矿山资料选择矿块利用系数取0.10~0.25;设定矿块的生产能力为3 600 t/d,但受到开采条件和工程设备的影响,矿块生产能力有一定的波动性,本设计矿块生产能力取值在2 000~4 000 t/d比较合适;该矿山是钼铅锌多金属大型矿山,在300 m标高以上矿体夹石含量比较高,副产矿石率波动比较大,在这里取5%~20%范围较合理;该矿山处在东北地区,由于地质构造和温度等原因对矿山开采有一定的影响,取地质影响系数0.8~1.0。
2.1.2 参数的随机取样
生产中段可布的矿块数、矿块利用系数、副产矿石率、矿块生产能力和地质影响系数都是不确定性的。现在约束范围内随机取20 000个关于N、k、z、E、q的序列数(i=1~20 000),见表1(表中取部分数据)。

表1 不确定参数N、k、z、E、q随机取样
2.1.3 基于Monte Carlo生产能力可信度的数值模拟
设功能函数f(x)等于按可布矿块数确定的中段生产能力A,用f(x)表示A,即:

式中:xi表示生成的第i个x,生成了多少个x,就可以计算出多少个f(x)的值。计算f(xi)的值,利用循环语句编制[程序1],设计计算满足条件的x个数m:m初始赋值为0。
程序中,y是f(xi)要满足的条件,分别代表首采中段的年生产能力300万t,500万t,750万t。最后计算满足y条件的x个数为m,得到满足条件的概率,见式(4):


图1 矿块布置图
式中:j=1,2,3,分别代表首采中段的年生产能力大于300万t,500万t,750万t的序号。按式(3)计算,分别得到首采中段的年生产能力大于300万t,500
万t,750万t的可信度指标,结果见表2。

表2 根据可布矿块数验证矿山首采中段年生产能力可信度
综合表1随机取样的结果和分析结果表2,当首采区设在350 m,按新中段准备时间验证年生产能力达到300万t的生产规模设计要求的可信度均达到99.9%以上,完全可以满足300万t/a的生产能力;年生产能力达到500万t的生产规模的平均可信度均达到93.6%,可以满足500万t/a的生产能力;年生产能力达到750万t的生产规模设计要求的平均可信度均为69.9%,要达到年生产能力750万t,就必须加大掘进量,这需要投入较多的人力物力,增加成本。
2.2 按新中段准备时间进行验证
2.2.1 基于不确定理论的计算公式
为保证矿山能持续生产,必须使新阶段开拓、采准等准备时间小于开采一个阶段所需的时间,因此,矿山生产能力受到新阶段准备时间的限制。新阶段开拓、采准等准备时间,根据设计矿山实际采用的机械水平和掘进工作条件及技术管理水平等情况,通过排采掘进度计划得出。
由于设计时间较短,对新中段的巷道布置工程量参考首采中段巷道布置工程量,首采中段巷道布置如图2所示。石门斜坡道s1长882 m,两条穿脉巷道s2长802 m,回风石门s3长57 m,运输大巷s4长600 m,回风大巷s5长588 m。
当穿脉巷道掘进好以后运输大巷和回风大巷就可以同时掘进。该矿山一年工作11个月,计算新阶段准备时间T按公式(5)计算,中段生产能力按公式(7)计算:

式中:A为中段生产能力/万t·a-1;T为新阶段准备时间/a;v为井巷掘进速度/m·月-1,取100~170;Q为生产中段可利用矿量,2 334.3万t;α为综合回收率,取85%~95%;β为矿石贫化率,取5%~15%;E为地质影响系数,取为0.8~1.0;ω为超前系数,取1.2~1.5。

图2 开拓巷道布置图
根据所设计的井巷掘进进度和掘进所用的凿岩、运输设备,井巷掘进的速度开始时比较慢,后期会逐步提高,故取井巷掘进速度在100~170 m/月;超前系数值视矿床埋藏要素稳定情况而定,矿床埋藏要素稳定,有用矿物分布均匀,ω=1.2~1.5。
2.2.2 参数的随机取样
现随机在约束范围内取20 000个关于α、E、β、ω、v的数据,见表3(表中取部分数据)。

表3 不确定参数α、E、β、ω、v随机取样
2.2.3 基于Monte Carlo生产能力可信度的数值模拟
设功能函数f(x)等于按新中段准备时间确定的中段生产能力A,即:

用式(9)代替式(3),并将运行结果代入式(4),得到按新中段准备时间验证首采中段的年生产能力时,年生产能力分别大于300万t,500万t,750万t的可信度指标,结果见表4。
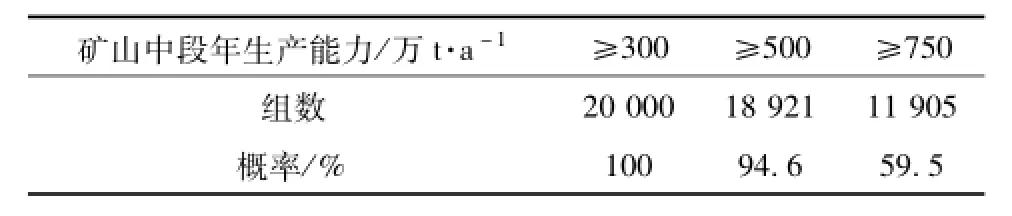
表4 根据新中段准备时间验证矿山首采中段年生产能力可信度
综合表3随机取样的结果和分析结果表4,当首采区设在350 m,按新中段准备时间验证年生产能力达到300万t的生产规模设计要求的可信度均达到99%以上,完全可以满足300万t/a的生产能力;年生产能力达到500万t的生产规模的平均可信度均达到94.6%,可以满足500万t/a的生产能力;年生产能力达到750万t的生产规模设计要求的平均可信度均为59.5%,要达到年生产能力750万t,就必须加大掘进量,这需要投入较多的人力物力,增加成本。
3 结 论
本文针对生产能力验证的多个不确定性因素,应用Monte Carlo法原理对不确定性因素进行随机取样,运用电子计算机实现统计模拟或抽样的计算。从两个方面的多个不确定性因素进行随机抽样分析,以确定生产能力达标的可信度的分析,根据Monte Carlo法的统计结果表明,该矿在现有的条件下,达到300万t/a的可信度接近100%,达到500万 t/a的生产能力的可信度分别为93.6%和94.6%,因此300万t/a和500万t/a在现有的条件下完全可以达到。然而,达到750万t/a的生产能力的可信度分别为69.6%和59.5%,因此如果要达到750万t/a的生产能力,必须加大掘进量,这需要投入较多的人力物力,增加成本。可以采用两个中段同时开采,加强掘进工作,保证掘进设备的完好率,提高掘进速度,保证采掘平衡。
综上所述,Monte Carlo法在进行多个不确定性因素的分析具有较大的优势,且适于计算机编程,为用户提供了方便,经本例运行,已验证其实用性和准确性。
[1] 邓秉德,庞晓波,黄妙棋.基于蒙特卡罗模拟方法的城市内涝灾害风险分析[J].统计观察,2015,20:111-115.
[2] 陈怀艳,曹芸,韩洁.基于蒙特卡罗法的测量不确定度评定[J].电子测量与仪器学报,2011,4(25):301-308.
[3] 王伟,宋明顺,陈意华,等.蒙特卡罗方法在复杂模型测量不确定度评定中的应用[J].仪器仪表学报,2008,29(7):1 446-1 449.
[4] 李筠,祝勇.Monte Carlo方法在测量不确定度评定中的应用[J].仪器仪表学报,2006,27(6):1 282-1 283.
[5] 刘文文,葛乐矣.基于蒙特卡罗方法的虚拟仪器测量不确定度评估[J].电子测量与仪器学报,2007,21(3):56-60.
[6] 崔孝海,曲璐.蒙特卡罗方法在微波功率测量不确定度分析中的应用[J].计量学报,2008,29(1):77-79.
[7] 雷桂媛.关于蒙特卡罗及拟蒙特卡罗方法的若干研究[D].杭州:浙江大学,2003.
The Validation of Production Capacity of Large and Thick O re Body First Stope Based on M onte Carlo M ethod
LIU Bin1,REN Qing-yun2
(1.Yunnan Yanfa Mining Technology Co.,Ltd.,Kunming 650200,China;2.Hunan Research Institute of Nonferrous Metals,Changsha 410100,China)
According to the feasibility study report of a lead-zinc mine in Heilongjiang province,validate the mining design and production capacity of first stope.The mine production capacity was validated by the Monte Carlo method.Themainly aim is to validate the number of ore block and newmiddle preparation time.The results show that the Monte Carlo method has a good advantage for the analysis of reliability verification.And the verified result is consistentwith the results of feasibility report.
Monte Carlo;first stope;production capacity validation
TD853.2+5
A
1003-5540(2016)02-0010-04
2016-03-10
刘 彬(1986-),男,助理工程师,主要从事矿山设计、研究工作。
