“随机信号分析”课程中功率谱及估计的研讨

刘明骞， 李兵兵， 郭万里

(西安电子科技大学 通信工程学院， 陕西 西安 710071)

“随机信号分析”课程中功率谱及估计的研讨

刘明骞， 李兵兵， 郭万里

(西安电子科技大学 通信工程学院， 陕西 西安 710071)

本文首先分析“随机信号分析”课程中功率谱密度和自相关函数，然后分别介绍了功率谱的估计方法，并以实验为例说明功率谱的估计方法，最后以无线通信系统中OFDM信号的带宽估计为例，说明功率谱估计方法在实际工程中的应用。本文对于功率谱及其估计的教学有一定的指导作用，并且有助于学生更好地理解理论和工程应用。

随机信号分析；功率谱；维纳辛钦定理；功率谱估计

0 引言

功率谱及其估计是“随机信号分析”课程教学中的重要部分，对于工程应用中谱估计有着重要的指导意义[1-3]。

关于功率谱的教学，重点在于理解功率谱密度的定义和性质、掌握功率谱密度与自相关函数的关系、功率谱估计的方法及其运用。在理论教学和实验教学中，学生普遍反映功率谱估计的方法难以掌握和应用。

笔者认为，在功率谱的教学中不能脱离实际的工程应用背景，在“随机信号分析”课程教学中，展开功率谱及功率谱估计的研讨是有必要的。

1 功率谱

1.1 功率谱密度

由实平稳过程X(t)的样本函数x(t)构造一个截尾函数xT(t)，其表达式为

(1)

对样本函数x(t)在时间区间(-T,T)内求其时间平均功率为

(2)

其中，Fx(ω,T)为xT(t)的傅里叶变换。令T→∞，则x(t)在(-∞,∞)上的平均功率为

(3)

其中，等号右边表达式被称作函数x(t)的平均功率谱密度，简称功率谱密度[1]。将上述关于确定函数x(t)的功率谱密度的概念推广到随机过程X(t)，可得随机过程X(t)的功率谱密度为

(4)

上述的功率谱密度SX(ω)又称为“双边谱密度”，对ω的正负值都是有定义的。在工程上为了便于实际测量，常根据平稳过程的SX(ω)的偶函数性质把负频率范围内的谱密度折算到正频率范围内，从而定义“单边谱密度”GX(ω) ，表示为

(5)

单边谱密度有时也称为物理谱，GX(ω)和SX(ω)之间的关系如图1所示。一般在讨论到功率谱密度时，若不加说明，则指双边谱密度。

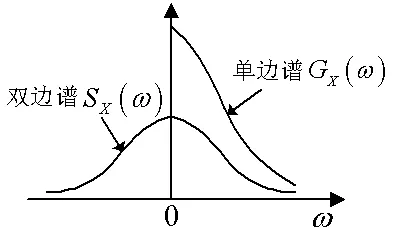
图1 单边谱和双边谱之间的关系

1.2 功率谱密度与自相关函数的关系

对于平稳过程X(t)，其自相关函数RX(τ)和功率谱密度SX(ω)是一对傅里叶变换：

(6)

在此假设RX(τ)满足绝对可积的条件，这就是维纳—辛钦定理[4]。

利用自相关函数RX(τ)和功率谱密度SX(ω)均为偶函数的性质，可将式(6)写成另外一种形式：

(7)

在实际问题中，一些平稳过程的自相关函数或功率谱密度的傅里叶变换或逆变换通常是不存在的，若利用δ函数的傅里叶变换的性质，就可解决此问题。

2 功率谱的估计

功率谱密度函数表示随机信号各频率成分的功率分布情况，在随机信号处理中应用广泛。功率谱的估计方法一般分为两大类：一类是线性估计法，又称经典法，线性估计法是有偏的谱估计方法，功率谱的分辨率随数据的长度增加而提高，主要包括自相关法、自协方差法和周期图法等经典谱估计以及AR模型的现代谱估计[4]。另外一类是非线性估计法，非线性估计方法大多是无偏的谱估计方法，可以获得高的谱分辨率，主要包括最大似然法、最大熵法等[5]。

2.1 功率谱的线性估计法

功率谱的线性估计法可以分为经典谱估计和现代谱估计。下面我们以周期图法为例来介绍经典谱估计方法。

周期图法通过计算x0,x1,…,xN-1的离散傅里叶变换X(ejω)，再取其幅频特性平方乘以1/N作为功率谱估计，其表达式为

(8)

(9)

由于经典谱估计不是功率谱的一致估计，而且当N值愈大时起伏更加激烈， 因此需要对此进行改进。在实际应用中，功率谱估计改进的途径大致有两种：一种是对同一过程作多次周期图估计，再加以平均；另外一种是用加窗的办法对单一功率谱估计加以平滑。

2.2 功率谱的非线性估计法

功率谱的非线性估计法主要包括最大似然法、最大熵法等。下面我们以最大似然法为例来简单介绍非线性估计方法。

让信号通过一个滤波器，通过选择滤波器的参数使所关心的频率的正弦波信号能够无失真地通过，同时，使所有其他频率的正弦波通过这个滤波器后输出的均方值最小。在这个条件下，信号经过这个滤波器后输出的均方值就作为其最大似然法的功率谱估值。

3 功率谱估计的实验设计

在此，给出一个功率谱估计的实验，通过该实验使学生能掌握几种功率谱分析方法并能进行对比，以便学生能够学以致用。

实验的参数设置为：输入信号为方波信号x(t)，方波信号基频为1 kHz，幅值为1 V，n(t)为白噪声，其中输入信号的时域波形图如图2所示。自选Matlab或C/C++仿真软件之一编程和仿真。

通过周期图法和最大似然法编写仿真程序并正确地运行程序，用波形图来表示出仿真的结果，对这两种功率谱估计的方法进行比较分析，总结它们各自的特点。

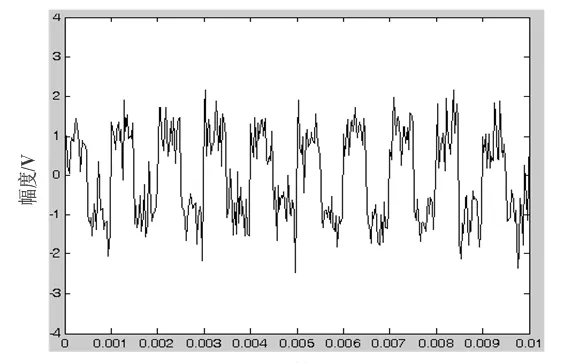
图2 输入信号的时域波形图

4 功率谱估计的应用

学生在学习功率谱的定义和性质，以及功率谱估计理论的过程中，往往希望教师能够说明其在工程或科研实践中的应用，从而实现理论与实际的结合。本部分以无线通信系统中OFDM信号的带宽估计为例，说明功率谱估计方法的工程应用。

OFDM信号的带宽估计主要涉及三个步骤：步骤一是估计OFDM信号的功率谱；步骤二是消噪处理；步骤三是OFDM信号带宽的计算，其中步骤二和步骤三可以参考文献[4]和[5]，步骤一的OFDM信号的功率谱估计可以采用上述的线性估计方法，本文分别以修正的平均周期图法和AR模型的现代谱估计方法为例进行分析说明。

4.1 修正的平均周期图法(Welch 法)

将长度为N的数据x(n),n=0,1,…,N-1分成L段，每段有M个数据，第i段数据表示为

xi(n)=x(n+iM-M), 0≤n≤M，1≤i≤L

(10)

然后把窗函数w(n)加到每一个数据段上，求出每一段的周期图，第i段的周期图为

体育课不同于文化课，它大多是室外课，或多或少会有一些突发事件发生，对于这些突发事件的处理，老师要灵活机智，以敏税的眼光和机智的语言引导学生，巧妙地应对和化解课程教学中的各种“意外”，让学生以大无畏的精神迎难而上，提高学生积极参与体育运动的热情。

(11)

式中，U被称为归一化因子，

(12)

将每一段的周期图之间近似看成互不相关，最后功率谱估计为

(13)

对式(13)求统计平均，得到

(14)

式中，

(15)

通过该方法可估计出OFDM信号的功率谱，如图3所示[7]。

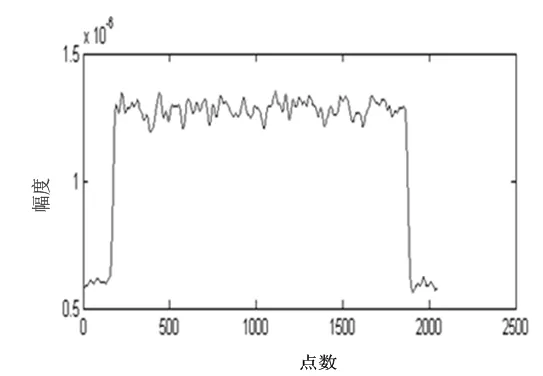
图3 基于Welch法的OFDM功率谱估计

4.2 AR模型的现代谱估计方法

(16)

其中x(n),n=1,2…,N是长度为N的数据，w(n)是均值为0，方差为σ2的白噪声序列，m为AR模型的阶数，ak(k=1,2,…,m)为AR模型的参数。由式(16)可得AR模型的转移函数为

(17)

则得到AR模型功率谱估计表达式为

(18)

其中，ω为角频率.

在此，利用AIC准则作为AR模型的定阶准则估计阶数m[6]；采用伯格法估计AR模型的参数ak和白噪声序列的方差σ2[4]；则按AR模型进行OFDM信号的功率谱估计，其仿真结果如图4所示[7]。

图4 基于AR模型的OFDM功率谱估计

5 结语

本文分析了功率谱密度与自相关函数的关系以及功率谱的线性估计法和非线性估计法。由分析可见，功率谱及其估计涉及到维纳辛钦定理和信号检

测估计理论。功率谱及其估计内容教学中，不但需要理论教学，而且需要加强实验举例和实际的工程应用，让学生能够学以致用，从而能够更好地对理论内容进行理解和应用。

[1] 李兵兵，马文平，田红心等编. 随机信号分析教程[M]. 北京: 高等教育出版社, 2012年7月

[2] 蔡剑华，王先春. 基于LMD-Teager变换的功率谱估计[J]. 上海: 中国激光, 2015, 42(3): 0315001-1-0315001-7

[3] 李静威，全厚德. 脉冲噪声条件下的相关熵谱估计 [J]. 北京: 信号处理, 2014, 30(8): 944-948

[4] 高西全，丁玉美. 数字信号处理(第3版)[M]. 西安: 西安电子科技大学出版社, 2008年8月

[5] 赵树杰,赵建勋. 信号检测与估计理论[M]. 北京: 清华大学出版社, 2005年11月

[6] T.J. Ulrych and M. Ooe. Autoregressive and Mixed Autoregressive-Moving Average Models and Spectral[C] Nonlinear Methods of Spectral Analysis, New York, 1983:73-125.

[7] 刘明骞，李兵兵，王婧舒. 多径信道下的OFDM信号带宽盲估计 [J]. 武汉: 华中科技大学学报(自然科学版), 2011, 39(10): 79-82

Discussion on Power Spectrum and Estimation of Random Signal Analysis Course

LIU Ming-qian, LI Bing-bing, GUO Wan-li

(SchoolofTelecommunicationsEngineering,XidianUniversity,Xi'an710071,China)

This paper firstly analyzes the power spectrum density and the autocorrelation function in Random Signal Analysis course. And then, the estimation methods of the power spectrum are introduced and illustrated by experiments respectively. Finally, the bandwidth of OFDM signal in wireless communication system is estimated as an example to illustrate the application of the power spectrum estimation method in practical engineering. This paper has some guidance to the teaching of power spectrum and its estimation, and it is helpful for the students to better understand the theory and engineering application.

random signal analysis; power spectrum; Wiener-Khintchine theorem; power spectrum estimation

2015-07-06;

2015-09- 27

西安电子科技大学教学质量提升计划项目(5050011401)

刘明骞(1982-)，男，博士后，讲师，主要从事随机信号分析教学、通信信号处理和认知无线电的研究，E-mail：mqliu@mail.xidian.edu.cn

G423

A

1008-0686(2016)03-0084-04