山区非规则梁桥地震易损性分析研究

吴立人

(安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088)

山区非规则梁桥地震易损性分析研究

吴立人

(安徽省交通规划设计研究总院股份有限公司，安徽 合肥 230088)

地震作用下，山区非规则梁桥的震害明显高于常规梁桥，采用地震易损性分析方法能够较好地获得山区非规则梁桥在不同地震水准作用下的地震响应规律及其震害机理，从而实现更加有效的桥梁抗震设计。

桥梁抗震；山区；非规则梁桥；地震易损性分析

0 引 言

在山区和丘陵地带,由于地势起伏较大,使得各桥墩高度差异、跨径差异等均显著大于平原地区。因此,山区和丘陵地带存在大量的非规则梁桥。非规则梁桥由于存在高模态效应的影响,使其遭受到的地震响应和震害要比规则梁桥更大,即山区非规则梁桥的地震易损性更大,这在历次震害资料中都得到了充分体现,例如2008年的汶川地震[1-4],大量的非规则梁桥发生了严重震害甚至倒塌,造成了重大的次生灾害,严重阻碍了抗震救灾。因此,本文将基于性能的桥梁抗震设计理论及其地震易损性分析方法应用于山区非规则梁桥的抗震设计[5-8],以期提高设计有效性和合理性。

1 桥梁实例

本文以安徽省某山区高速公路上的一座非规则六跨连续梁桥作为算例桥梁,跨径组合为6×30 m,具体见图1。桥梁上部结构为30 m预应力混凝土组合箱梁。下部结构中,1号桥墩采用独柱墩,直径为2.4 m,桩基采用双排桩;其余桥墩均采用双柱墩,直径1.4 m,单排桩基础;桥台采用柱式桥台,直径1.5 m,单排桩基础;墩台桩基均按嵌岩桩设计,桩径均为1.5 m。

在算例桥梁有限元模型中,主梁采用弹性梁柱单元模拟,桥墩采用考虑沿单元长度分布塑性的基于力的非线性梁柱单元进行模拟,桥墩截面采用纤维单元进行离散,考虑了几何非线性(P-Δ效应)和材料非线性。算例桥梁纵桥向采用板式橡胶支座和聚四氟乙烯滑板式橡胶支座,在地震作用下可采用双线性的恢复力-位移模型,并利用零长度单元模拟支座。通过土弹簧考虑土-结构相互作用,利用零长度单元模拟土弹簧。算例桥梁的有限元模型见图2。

通过结构动力特性分析可知,在纵桥向,第一阶模态的质量参与系数最大,为0.766;在横桥向,第三阶和第五阶模态的质量参与系数较大,分别为0.643和0.131。因此,算例桥梁作为非规则连续梁桥,在纵、横桥向均存在一定的高模态效应,且横桥向更显著一些。

图1 算例桥梁立面图

图2 算例桥梁有限元模型

2 概率地震危险性分析

本文主要针对算例桥梁纵桥向的地震易损性进行分析,故选择第一阶模态周期所对应的谱加速度Sa(T1)作为地面运动强度参数(IM)进行工程场地的概率地震危险性分析,并获得分别对应于50年50%、50年10%和50年2%超越概率的一致危险性反应谱,见图3。同时,根据一致危险性反应谱分别选择了三组与之相匹配的实际地震波,分别模拟不同超越概率的地震动。

在地震工程学中,50年50%、50年10%和50年2%超越概率下的地震风险水平对应的平均回归期分别是72 a、474 a和2 475 a,由于IM服从对数正态分布,根据回归期与IM在对数空间的线性拟合可以获得工程场地的地震风险曲线,见(1)式,即地震风险模型。因此,根据图4中的线性拟合可以获得算例桥梁工程场地的地震风险曲线,即

λ(IM)=0.000 006 22(IM)-2.485 73。

(1)

其中,k0和k为回归系数。

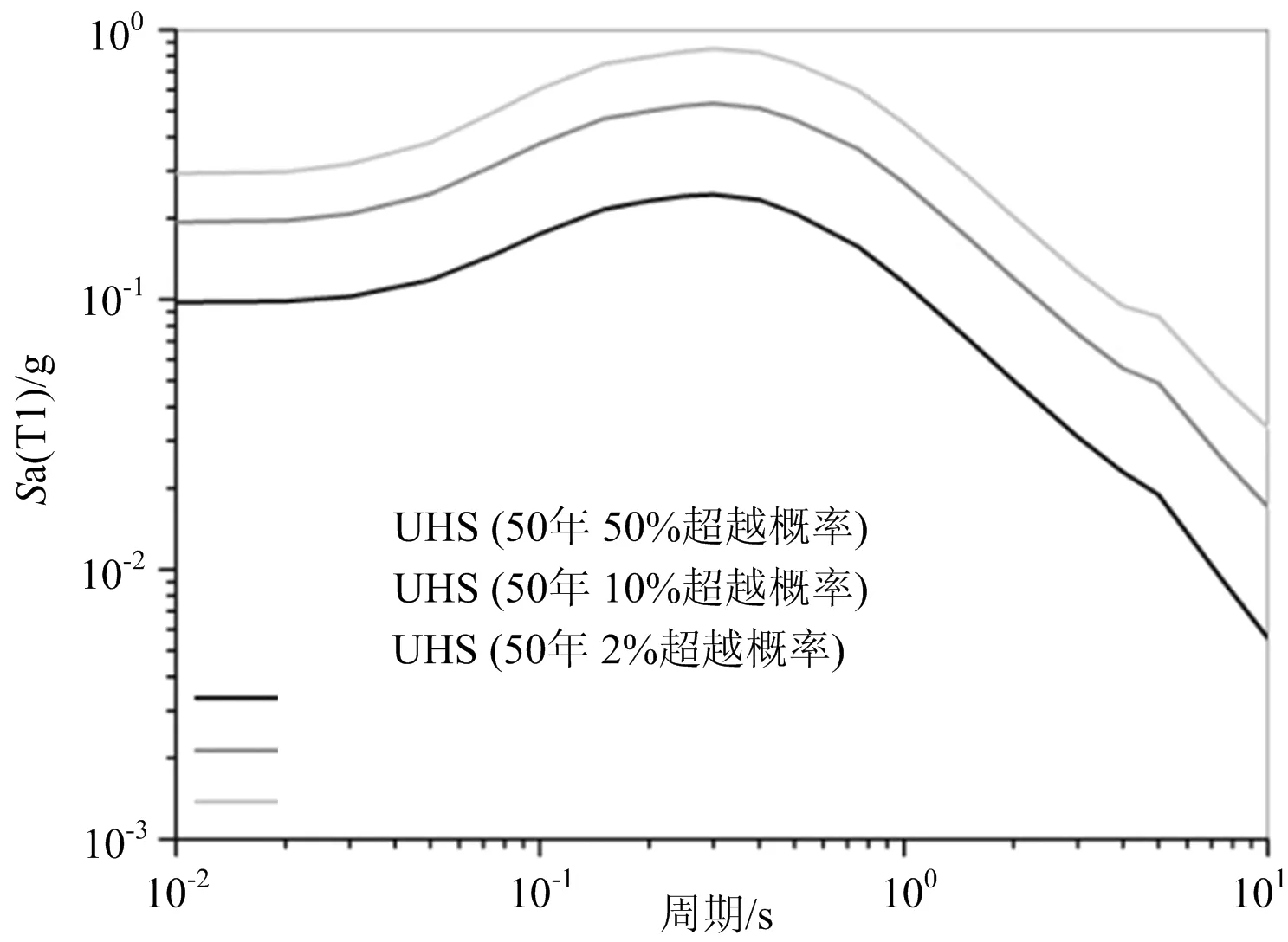
图3 工程场地一致危险性反应谱

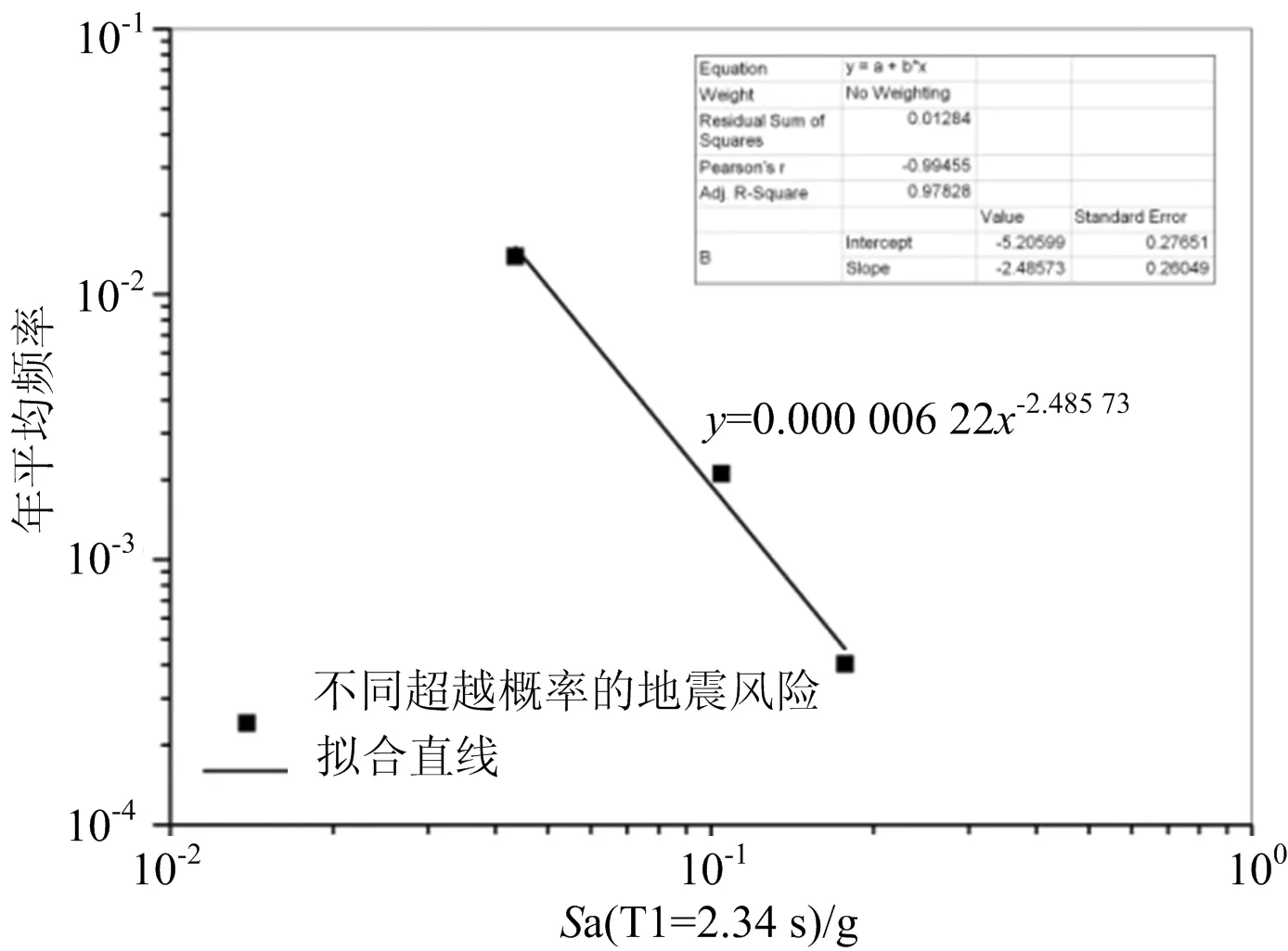
图4 工程场地的地震风险曲线

3 概率地震需求分析

采用对应不同超越概率的三组实际地震波作为输入地面运动,对算例桥梁进行非线性动力时程分析,从而获得桥梁在不同地震水准作用下的地震响应,即工程需求参数(EDP,Engineering Demand Parameter)。本文选择墩顶漂移比作为工程需求参数,建立EDP风险曲线,其定义为墩顶的最大绝对位移与桥墩高度之比,反映了桥墩结构在地震作用下的最大变形能力,见(2)式。

(2)

其中,d为墩顶漂移比;|u|max为整个地震过程中墩顶的最大绝对位移;H为墩高。

在地震工程与结构抗震领域,特定IM水平下EDP的概率分布假定服从对数正态分布,因此,在概率地震需求分析中,需要将EDP表示为IM的函数,见(3)式,即在不同IM水平下对EDP的均值预计,可通过IM和EDP在对数坐标系内的线性拟合获得,见图5,本文只列出了1#桥墩的拟合直线,其他桥墩的拟合方法相同。

(3)

其中,a和b分别为回归系数。

因为EDP假定服从对数正态分布,故EDP超越某一特定值的概率可以用(4)式表示。

(4)

结合公式(1)和(4),可以获得在特定地震动强度水平(IM)下,桥梁地震响应超越某一特定值的概率,具体见公式(5)。通过IM和EDP的数学关系即(3)式,可以直接推导(5)式的解析解,从而获得EDP风险曲线,具体见(6)式。

(5)

(6)

通过以上计算,获得了算例桥梁各墩顶漂移比的EDP风险曲线,具体见图6。通过图6可以很清晰地获得各桥墩墩顶漂移比超越不同数值的概率,同时也可以对不同桥墩的地震响应大小进行对比分析。

图5 1#桥墩墩顶漂移比与Sa(T1)的拟合直线

图6 墩顶漂移比风险曲线

4 地震易损性曲线

桥梁地震易损性曲线表示在不同地震动强度水平下,结构地震需求Sd达到或超越不同破坏状态所对应的特定反应值Sc(即结构抗震能力)的条件概率,见(7)式。由于在本文中采用墩顶漂移比作为EDP,故仍将采用墩顶漂移比对桥墩的不同破坏状态进行定义,具体见表1所列。由于在结构抗震领域,假定Sc和Sd服从对数正态分布,故不同破坏状态下的失效概率Pf可以进一步转化为标准正态分布形式,具体见(8)式,其中Sd可用(3)式计算。

表1 桥墩破坏状态定义

(7)

(8)

其中,Pf为超越某一特定破坏状态的概率;Sc为结构抗震能力;Sd结构地震需求;βc和βd分别为结构地震需求和抗震能力的对数标准差。

根据美国HAZUS 99规定,当易损性曲线以谱加速度Sa作为自变量时,(βc2+βd2)1/2可取为0.4;以PGA作为自变量时,(βc2+βd2)1/2可取为0.5。因此,算例桥梁各桥墩超越不同破坏状态的概率即地震易损性曲线,具体见图7,文中只列出了各桥墩达到轻微破坏和中度破坏的地震易损性曲线,起到说明作用。

图7 各桥墩达到不同破坏状态的超越概率

通过分析地震易损性曲线可知:① 1#独柱墩在大震作用下几乎不可能发生严重破坏或倒塌。② 3#固定墩在地震作用下的易损性最大。③IM越大,高墩位移越大,也越容易发生以弯曲为主的破坏。因此,如果要采取抗震加固措施或制定震后维修计划时,首先应该针对固定墩进行,其次是高墩,然后是矮墩,而1#独柱墩抗震性能较好,但要注意其是否会发生剪切破坏或弯剪破坏。

5 结束语

采用地震易损性分析方法，能够获得在地震作用下有关桥梁地震响应规律及其震害机理的重要信息，并能直接应用于桥梁抗震设计。例如:① 某一构件在不同地震动强度水平下达到或超越各破坏状态的概率，即达到不同破坏状态的可能性。② 某一构件达到特定破坏状态所需要的地震动强度水平。③ 能够获得各种构件在不同地震动强度水平下的破坏顺序及其震害规律，从而为抗震设计和抗震构造措施的设置提供了重要的参考依据，有效提高了山区非规则梁桥的有效性和合理性。

[1] 杜修力，韩 强，李忠献，等. 5.12汶川地震中山区公路桥梁震害及启示[J].北京工业大学学报，2008, 34(12):1270～1279.

[2] 赵国辉，刘健新.汶川地震桥梁震害分析及抗震设计启示[J].震灾防御技术，2008, 3(4):363～369.

[3] 王东升，孙治国，郭 迅，等.汶川地震桥梁震害经验及抗震研究若干新进展[J].公路交通科技，2011, 28(10):44～53.

[4] 王东升，郭 迅，孙治国，等.汶川大地震公路桥梁震害初步调查[J].地震工程与工程振动，2009, 29(3):84～94.

[5] Mackie K, Stojadinovic B. Fragility curves for reinforced concrete highway overpass bridges [A]. 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 2004.

[6] Hesameddin A,Eduardo M.Probability-based seismic response analysis [J]. Engineering Structures. 2005(27):1151～1163.

[7] Kevin M，Bozidar S. Seismic Demands for Performance-Based Design of Bridges [R]. Pacific Earthquake Engineering Research Center, College of Engineering University of California, Berkeley. PEER Report 2003/08.

[8] Lee, TH，Mosalam KM.Probabilistic seismic evaluation of reinforced concrete structural components and systems [R]. Pacific Earthquake Engineering Research Center, College of Engineering University of California, Berkeley. PEER Report 2006/04.

2016-11-02；修改日期：2016-12-01

吴立人(1957-)，男，江苏宜兴人，安徽省交通规划设计研究总院股份有限公司教授级高工．

U448.21;U442.55

A

1673-5781(2016)06-0779-04