基于风险偏好的PPP项目风险分担博弈模型

邵钰 王祖和

(山东科技大学经济管理学院,山东 青岛 266590)

基于风险偏好的PPP项目风险分担博弈模型

邵钰 王祖和

(山东科技大学经济管理学院,山东 青岛 266590)

基于风险偏好，在参与双方对彼此的信息、偏好都了解的情况下，运用完全信息静态博弈模拟解决由单方承担的风险问题。对于需要双方共担的风险则运用完全信息动态博弈模型——讨价还价模型，由此确定双方的最优分担比例。运用博弈的相关知识构建PPP项目中的风险分担模型，尤其当双方需要共同分担某一风险时，通过求解动态博弈的纳什均衡得出较为合理的风险分担比例。

PPP；风险偏好；风险分担；博弈

0 引言

公私合作(Public-Private-Partnerships，PPP)指吸引社会资本投入到基础设施的建设或提供某种公共物品或服务。政府以及代表着社会资本的私人部门通过组建项目公司的模式，进行项目的设计、融资、建设等，项目建成后以特许经营的形式，将项目的部分或者全部交由私人部门经营管理。这一融资模式的应用大大解决了我国财政预算的不足，同时也满足了我国对基础设施的需求。

“利益共享、风险共担、长远合作”是PPP项目模式的三个主要特点[1]。近些年，随着PPP项目融资模式的发展，风险分担问题随之而来，公平合理的风险分担是PPP项目成功的重要因素之一。目前在风险分担的过程中，还没有形成一种系统、科学的项目风险分担方法，存在着风险分担不合理，公私双方承担的风险比例与自身的实际不相符的问题。本文将针对这些问题展开研究。

1 研究现状

何涛等基于合作博弈理论，依据参与双方的风险偏好，提出了PPP项目风险分担过程中政府和私人部门之间的最优合作博弈模型[2]。李林等在参与方地位非对称的情况下，利用讨价还价博弈理论构建了PPP项目风险分担的讨价还价模型，并得出相对应的子博弈精炼纳什均衡[3]。朱向东等将项目风险主体设定为项目所有者、关联方和项目公司三方，基于此建立静态博弈风险分担模型[4]。葛果等建立三个主体的动态博弈模型，并给出基于风险偏好的三方合作博弈支付矩阵，由此计算出项目的风险分担决策解[5]。

2 风险分担原则

无论PPP项目的风险是单独由一方承担，还是双方共担某一风险，在合理公平的分担过程中都需要遵循一定的风险分担原则：①风险偏好系数大的一方所承担的风险比例较大；②风险承担比例与风险收益相匹配；③承担的风险要控制在一定范围内。

3 基于风险偏好的博弈模型

3.1 静态博弈模型的构建

模型的基本要素：

参与人：政府部门P方,代表社会资本的Q方。

得益:双方针对某一风险，在项目完成时的风险收益。

策略：针对某一风险双方都有(承担、不承担)两种策略。

对于P方：RP=R1×V-C1×V；对于Q方：RQ=R2×V-C2×V。R1-C1=X1为P方的风险偏好系数；R2-C2=X2为Q方的风险偏好系数。

P方、Q方在完全信息静态博弈下的得益矩阵如下：

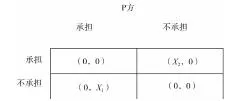
由此可以得出：

当X1>0,X2<0时，只有一个纳什均衡，即：Q方承担风险，P方不承担。

当X1<0,X2>0时，只有一个纳什均衡，即：P方承担风险，Q方不承担。

当X1>0,X2>0或X1<0,X2<0时没有唯一的纳什均衡点，这时需要双方对风险进行共同承担。

3.2 动态博弈模型的构建

模型的基本要素：

参与人、得益与静态博弈一致。

策略：针对某一风险双方分担的比例。

规则：可以由P方先出价，也可以由Q方先出价，这里假设P方先出价。

讨价还价模型基本假设条件：

(1)双方都知道彼此的策略及对某风险的偏好情况，属于完全信息动态博弈。

(2)风险初始值设为1。

(3)P、Q双方都是理性人，都不希望谈判破裂。

(4)针对P方承担风险的比例P，及Q方承担的风险比例1-P展开讨价还价。

第一种情况：当X1>0,X2>0时。

此时风险的发生会给双方带来风险收益。讨价还价过程中随着谈判时间的延长，项目风险不断变化，风险收益不断降低，设P、Q双方的风险折损系数分别为δ1,δ2(0<δ<1)。同时在讨价还价过程中，每一阶段都需要花费大量的人力、物力资源，因此设一次讨价还价的双方的成本都为c。

第一回合：

P方提出承担比例为：P1、1-P1，Q方同意则结束。此时P、Q双方承担风险分别为：P1、1-P1；P方的风险收益为：RP1=X1P1-c，Q方的收益为：RQ1=X2(1-P1)-c。Q方不同意，则进行第二回合的讨价还价。

第二回合：

Q方提出承担比例为：P2、1-P2，P方同意则结束。此时P、Q双方承担风险分别为：δ1P2、δ2(1-P2);P方的风险收益为：RP2=X1δ1P2-2c，Q方的收益为：RQ2=X2δ2(1-P2)-2c。P方不同意,则进行第三回合的讨价还价。

第三回合:

P方提出承担比例为：P3、1-P3，Q方同意则结束。此时P、Q双方承担风险分别为：δ12P3、δ22(1-P3)；P方的风险收益为：RP3=X1δ12P3-3c，Q方的收益为：RQ3=X2δ22(1-P3)-3c。Q方不同意,则进行第四回合的讨价还价(图1)。

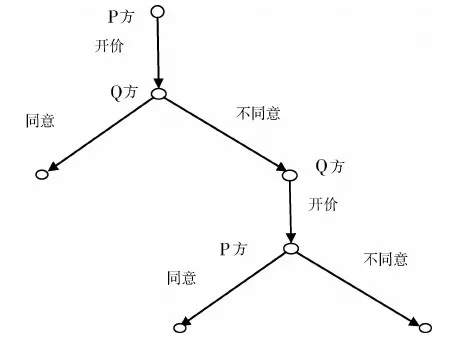
图1 P、Q双方讨价还价过程图

由于该模型是无限博弈模型，而在无限的讨价还价过程中，逆推点从第一回合开始和从第三回合开始结果都是一样的[6]。根据这一思路对PPP模式的讨价还价模型进行解答。

而对于三个回合的讨价还价过程，将第三回合作为逆推归纳的起点。第三回合，P方的风险收益为：RP3=X1δ12P3-3c；Q方的收益为：RQ3=X2δ22(1-P3)-3c。逆推至第二回合，为了避免谈判进入第三回合，Q方在第二回合的策略应该使得P方在该回合中的风险收益大于等于其在第三回合中的风险收益，同时也使得自己的风险收益最大化。因此，在第二回合中Q方的最优策略为

RP2=RP3

X1δ1P2-2c=X1δ12P3-3c

即

(1)

进而逆推至第一回合，P方的策略应该使得Q方在该回合中的风险收益大于等于其在第二回合的风险收益，同时使得自己的风险收益最大化。因此，第一回合中P方的最优策略为

RQ1=RQ2

X2(1-P1)-c=X2δ2(1-P2)-2c

即

(2)

由于第一回合与第三回合作为逆推点的结果都是一样的，由此可知

P1=P3

(3)

根据式(1)～式(3)可得P方分担比例为

(4)

Q方分担比例为：1-P*。

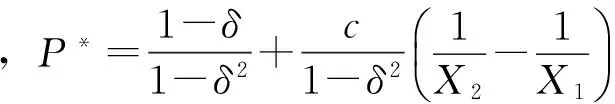
第二种情况：当X1<0,X2<0时。

此时风险的发生会给双方带来风险损失。在讨价还价过程中，随着谈判时间的延长，项目风险不断增大，风险损失不断增加，设P、Q双方的风险折损系数分别为δ1,δ2(δ>1)。同时一次讨价还价的成本为c。

第一回合，P方的风险损失为：CP1=-X1P1+c，；Q方的风险损失为：CQ1=-X2(1-P1)+c。

第二回合，P方的风险损失为：CP2=-X1δ1P2+2c，；Q方的风险损失为：CQ2=-X2δ2(1-P2)+2c。

第三回合,P方的风险损失为：CP3=-X1δ12P3+3c，；Q方的风险损失为：CQ3=-X2δ22(1-P3)+3c。

同理，逆推至第二回合，为了避免谈判进入第三回合，Q方在第二回合的策略应该使得P方在该回合中的风险损失小于等于其在第三回合中的风险损失，同时也使得自己的风险损失最小化。因此，在第二回合中Q方的最优策略为

CP2=CP3

进而逆推至第一回合，P方的策略应该使得Q方在该回合中的风险损失小于等于其在第二回合的风险损失，同时使得自己的风险损失最小化。因此，第一回合中P方的最优策略为

CQ1=CP2

并可得出P方分担比例为

Q方分担比例为：1-P*。

P*的表达式与X1>0,X2>0时的表达式一致，说明无论风险偏好都为正还是都为负，双方最优策略的均衡表达式都一样，即：将风险损失降到最低或将风险收益最大化时，最优分担比例与双方的风险偏好的关系是一定的。

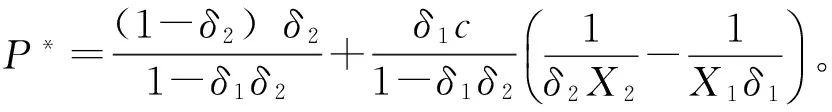
4 个案分析

青岛地铁X号线是青岛市地铁轨道交通规划中的一条线路，该线路全长约60km，有地下站点40座，是主城区连接黄岛及城阳区的骨干线路。该线路总投资403亿元，项目资本金约161.2亿元，由青岛市政府与中选社会投资人共同投资设立“青岛城市发展1号基金”，合作期限为25年。

笔者向与项目密切相关的人员咨询，通过采取问卷调查、面谈等方法，了解到该项目实施过程中可能遇到的风险有：政治法律变更、政府审批延误、税收调整等政治法律风险；通货膨胀、利率外汇变动等金融风险；工程建设、技术复杂、完工等建设风险；市场需求、运营、类似项目竞争等市场风险；地质文物、土地获得、环保等环境风险；地震、火灾、不可抗力等自然风险。通过对数据的分析，得出以下相关参数(表1)。

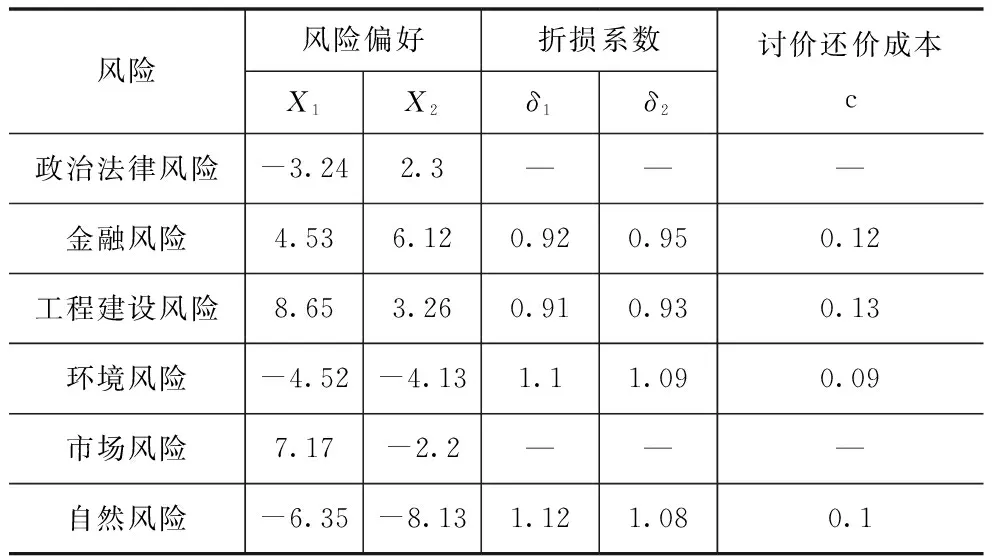
表1 地铁X号线项目风险相关参数

通过相关博弈可得，政治法律风险由政府单独承担，市场风险由代表社会资本的私人部门承担，而金融、环境、自然、工程建设等风险需要双方共担，双方分担的比例需进行下一步讨论。

假设讨价还价过程是由P方先出价，对于金融风险，X1>0,X2>0，根据式(4)可得出：P方承担的最佳比例为P*=0.34，则Q方承担1-P*=0.66。

对于工程建设风险，X1>0,X2>0，得出P方承担的最佳比例为P*=0.61，则Q方承担1-P*=0.39。

对于环境风险，X1<0,X2<0，得出P方承担的最佳比例为P*=0.46，则Q方承担1-P*=0.54。

对于自然风险，X1<0,X2<0，得出P方承担的最佳比例为P*=0.37，则Q方承担1-P*=0.63。

这几类风险只是整个项目中的几个具有代表性的风险类型，而项目中还有其他一些显性的或者隐形的风险，同时每个风险也可细分为多个更具体的风险，在项目实施过程中需要更加详细的划分比例，这里不再多加描述。

5 结语

本文运用静态博弈、动态博弈的相关知识构建了PPP项目中的风险分担模型，尤其当双方需要共同分担某一风险时，通过求解动态博弈的纳什均衡可以得出较为合理的风险分担比例，同时也符合风险偏好系数大的一方分担较多的风险。在参与双方之间达成协议，使得双方的风险损失降到最低，获取较高风险收益，使得双方实现共赢局面，精诚合作，促进项目的成功。

[1] Akintoye A，Beck M，Hardcastle C.Public-private partnerships：managing risks and opportunities[M].Oxford：Blackwell Science，2003.

[2] 何涛，赵国杰.基于随机合作博弈模型的PPP项目风险分担[J].系统工程,2011(4):88-92.

[3]李林,刘志华,章昆昌.参与方地位非对称条件下PPP项目风险分配的博弈模型[J].系统工程理论与实践,2013,33(8):1940-1948.

[4]朱向东,肖翔,征娜.基于三方博弈模型的轨道交通PPP项目风险分担研究[J].河北工业大学学报,2013(2):97-101.

[5]葛果,侯懿.基于风险偏好的PPP项目风险分担的三方博弈模型[J].四川理工学院学报:自然科学版,2015,28(1):87-91.

[6]谢识予.经济博弈论[M].2版.上海：复旦大学出版社，2002.PMT

2016-04-27