斜入射椭圆余弦波对直立防波堤的波浪渗流作用*
2016-06-05朱梦华詹杰民陈瑞志
朱梦华,黄 华,詹杰民,张 敖,郭 霖,陈瑞志
(中山大学应用力学与工程系,广东 广州 510275)
斜入射椭圆余弦波对直立防波堤的波浪渗流作用*
朱梦华,黄 华,詹杰民,张 敖,郭 霖,陈瑞志
(中山大学应用力学与工程系,广东 广州 510275)
基于椭圆余弦波的浅水波理论,结合对Biot波浪渗流固结理论的推广应用,给出了固立于可渗透海床上的直立防波堤在浅水波斜入射条件下的反射波问题的数学解,并据此通过特征函数展开法推导了浅水波引起的海床内渗流压力的解析解式,同时计算了作用于防波堤底部的浅水波波浪渗流浮托力和倾覆力矩且与水平波浪力和力矩进行了比较。计算结果表明,在一定条件下,椭圆余弦波的波浪渗流载荷与波浪的直接载荷可能具有相同量级。浅水波入射角、海水和渗流条件以及防波堤几何条件等因素的相对变化对波浪渗流载荷均存在一定的影响,其中对渗流倾覆力矩的影响更为明显。椭圆余弦波理论所给波浪渗流载荷的估值明显高于浅水条件下Airy波理论的对应估值,反映了水波非线性因素的影响效应。
椭圆余弦波;直立防波堤;斜入射与反射;可渗透海床;波浪渗流载荷
直立型防波堤是近岸工程应用最为广泛的一种防波堤形式,它的稳定性不仅取决于自身的重量和波浪冲击力,还与其底部可能承受的波浪渗流作用密切相关[1]。当防波堤固立于可渗透海底上时,往复的波浪水压力通过海底使得海床内土体超静空隙水压力变化,形成海床内渗流压力。所以,对于固立于可渗透海床上的防波堤,除考虑波浪作用外,一般还需要考虑波浪所致渗流压力对其底部的作用[2]。朱梦华等[3]、邹志利等[4]采用Airy波模型和Biot波浪渗流固结理论对直立式防波堤底基下海床中波浪渗流压力进行了解析求解。倪寅等[5]对多孔海床在波浪作用下渗流特性进行了数值模拟。曾昭銮等[6]应用Airy波模型对均匀海中的大直径透空圆柱上的波浪渗流力进行了解析研究。黄华等[7]对二层海中固立圆柱的波浪渗流作用问题进行了解析研究。陈瑞志等[8]对作用于透空复合圆柱的波浪渗流力进行了解析计算。黄华等[9]对二层海中的大直径透空圆环墩柱所受的波浪绕射力和波浪渗流力进行了计算。
上述关于波浪渗流作用的研究大多采用线性波模型,然而防波堤属近岸工程结构,所处水域主要为浅水区。当波浪从深水传入浅水后,波面形状将发生变化:波峰变陡,波谷变平,呈现出非线性波的特征。李奇等[10]应用非线性波理论解析计算了波浪对固立墩柱底部的波浪渗流作用。试验和理论研究表明,当波长与水深之比以及波高与水深比超过一定值时,波浪更适合采用椭圆余弦波等浅水波模型来予以描述。Isaacson[11]应用椭圆余弦波一阶理论对单一直柱的浅水波绕射作用进行了计算。朱梦华等[12]采用相同方法对直立防波堤的波浪力问题进行了研究。邱大洪等[13]应用椭圆余弦波理论研究了浅水立波对直墙的作用。徐云峰等[14]研究了椭圆余弦波作用下海床的响应问题。李奇等[15]采用椭圆余弦波模型对透空圆环柱的绕射问题以及波浪渗流问题展开了解析计算。Su Ming-de等[16]采用相同方法对对直立双柱的波浪绕射问题做了相关研究。
本文将椭圆余弦波一阶分量模型推广应用于Biot的波浪渗流固结理论中,应用特征函数展开法,推导了斜入射椭圆余弦波对固立于浅水区可渗透海床上的直立防波堤的波浪反射势解,并据此推导了由浅水波引起的海底下海床内渗流压力分布的解析解。所得结果是对已有的直立防波堤Airy波渗流理论的推广和拓展。通过对防波堤底部承受的波浪渗流浮托力和倾覆力矩的实际计算,并与Airy微幅波理论进行比较,揭示了浅水波条件下直立防波堤对斜入射波浪的反射作用规律以及由其引起的对防波堤底部的渗流作用规律。计算结果有效反映了浅水波非线性因素变化对波浪渗流载荷的可能影响。另外在波浪场和波浪渗流压力场的解析求解过程中,本文选用斜入射的水波入射条件,相比正入射而言更具普适性,且更接近实际波浪入射条件。
1 椭圆余弦波对防波堤的反射解
对于大尺度水下结构物,由于边界层厚度较小,海水可视为理想不可压缩无粘流体,且运动无旋,故波浪作用只需考虑水波绕射影响。再考虑水下结构固立于可渗透弹性海床上,依据Biot固结理论的相关假设[1],可设定立于海床上结构与海床间无相对滑动,海床内土体各向同性、可渗透且具有弹性性质,而海床底部不可渗透,无变形。由于一般情况下海床内渗流速度相远小于海底波浪场水流速度,故在绕射波浪场的求解中可不考虑海床内渗流对其影响,仍保留海底密实的固面条件。
图1所示为固立于浅水中可渗透海床上的无限长直立型防波堤,设水深为d,海床厚度为h,防波堤宽度为b,防波堤受到斜入射椭圆余弦波的作用,进而发生反射,其中入射角为α。可设浅水波反射波浪场流域为Ω,将波浪渗流压力场划分为V1、V2和V3三个区域。

图1 固立于浅水区中可渗透海床上的直立型防波堤Fig.1 Vertical breakwater resting on permeable seabed in shallow water
对于理想的无黏流体,设液体不可压缩且运动是无旋的,则对于在重力作用下的流体的波动可以应用速度势Φ来进行分析。设速度势总势、入射势和反射势分别为Φ、Φi和Φr,则对应波势的边值问题的一般提法为:
(1)
(2)
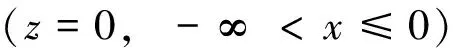
(3)

(4)

(5)

(6)
式中,η为波面;另反射波势φr须满足x=-∞处的辐射条件。
(7)
(8)
(9)
(10)
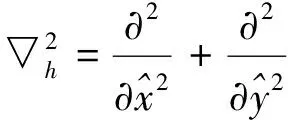
(11)

(12)
再将式(11)和(12)代入式(9),可得:
(13)
进一步采用摄动展开法,令
(14)
将式(14)代入式(13),归并σ0阶,可得:
(15)
对于二维正入射平面波,方程(15)的解为右行波解,即有χ0=χ0(x-ct)=χ0(kx-ωt),其中c、k和ω分别为波速、波数和波频。对与χ0相对应的椭圆余弦波一阶入射有量纲波势φi0(为方便计,仍写为φi)进行数学求解[6],可得:
(16)
式中,q=K(κ)(kx-ωt)/π;γ=E(κ)/K(κ);K(κ)和K(κ)分别为第一、二类完全椭圆积分;κ′2=1-κ2;cnq为雅克比椭圆函数,而模量κ由方程κ2K2(κ)=3π2H/4k2d3确定;另H表示波高,ω表示波频。
对上式积分,并将涉及cnq的积分项进行傅里叶级数展开,可得:
(17)
对于二维斜入射平面波,推广应用平面波一般理论,可得相应解式为:
(18)
式中,r为位置矢量,即r=(x,y);k为波数矢量,且k=(kx,ky)=(kcosα,ksinα)。

(19)

(20)
应用特征函数解法,结合考虑防波堤侧表面条件式(6),可得斜入射条件下椭圆余弦波一阶分量反射势和相应总势为:
(21)
(22)
(23)
(24)
2 椭圆余弦波引起的渗流作用解
本文将椭圆余弦波的浅水波模型推广应用于直立防波堤的波浪渗流作用问题研究。设海底下存在厚度为h的海床,海床底面不可渗透,斜入射浅水波遇到直立防波堤发生反射,海底处波浪压强为Pw=Re(pw),其中
(25)
如图1所示将渗流压力场划分为vj(j=1,2,3)三个区域。由Biot固结理论,海床内渗流压力场满足孔隙水压控制方程[1]。对应椭圆余弦波作用下直立型防波堤波浪渗流压力边值问题的提法为:
(26)
(27)
(28)
(29)
(30)
式中,vj(j=1,2,3)表示划分的三个不同渗流压力分布区域,且在界面上满足:

(31)

(32)

(33)
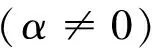
(34)
(35)
(36)
式中,
(37)
利用各渗流压力区交界面匹配条件式(31)和式(32),并根据函数系

(39)
(40)
(41)
式中,
(42)
由式(34)或(35)对防波堤底部积分,可得到椭圆余弦波作用下直立防波堤底部单位长度波浪渗流浮托力Fv=Re(fv)与倾覆力矩Mv=Re(mv),其中:
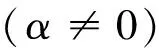
(43)
(44)
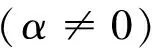
(45)
(46)
3 算例与分析
为方便计,图中以符号F统一代表防波堤单位长度水平波浪力或渗流浮托力幅值,以符号M统一代表防波堤单位长度水平波浪力矩或渗流倾覆力矩幅值。实算中,对所算的防波堤侧面单位长度上最大水平波浪力和力矩分别按因子ρg(H/2)d和ρg(H/2)d2进行无量纲化。对所算防波堤底部单位长度上所受最大浮托力和倾覆力矩分别按因子ρg(H/2)b和ρg(H/2)b2进行无量纲化。此外,在计算中引入参数λ,即λ=(4κ2/3π2)K(κ)=H/k2d3,它表示水波非线性影响因子,可以有效反映波浪特征与水深的相对变化所产生的水波非线性特征效应变化对波浪作用的可能影响。
图2为直立防波堤单位长度最大无量纲浅水波水平波浪力和力矩(不随入射角变化)随水波非线性影响参数λ的变化趋势结果。图中f1=F/ρg(H/2)d,m1=M/ρg(H/2)d2,分别表示单位长无量纲水平波浪力和力矩幅值。如图可见,波浪力和力矩幅值随着参数λ的增大而增大,说明浅水波非线性因素的增强将随之增大波浪对防波堤的直接作用。
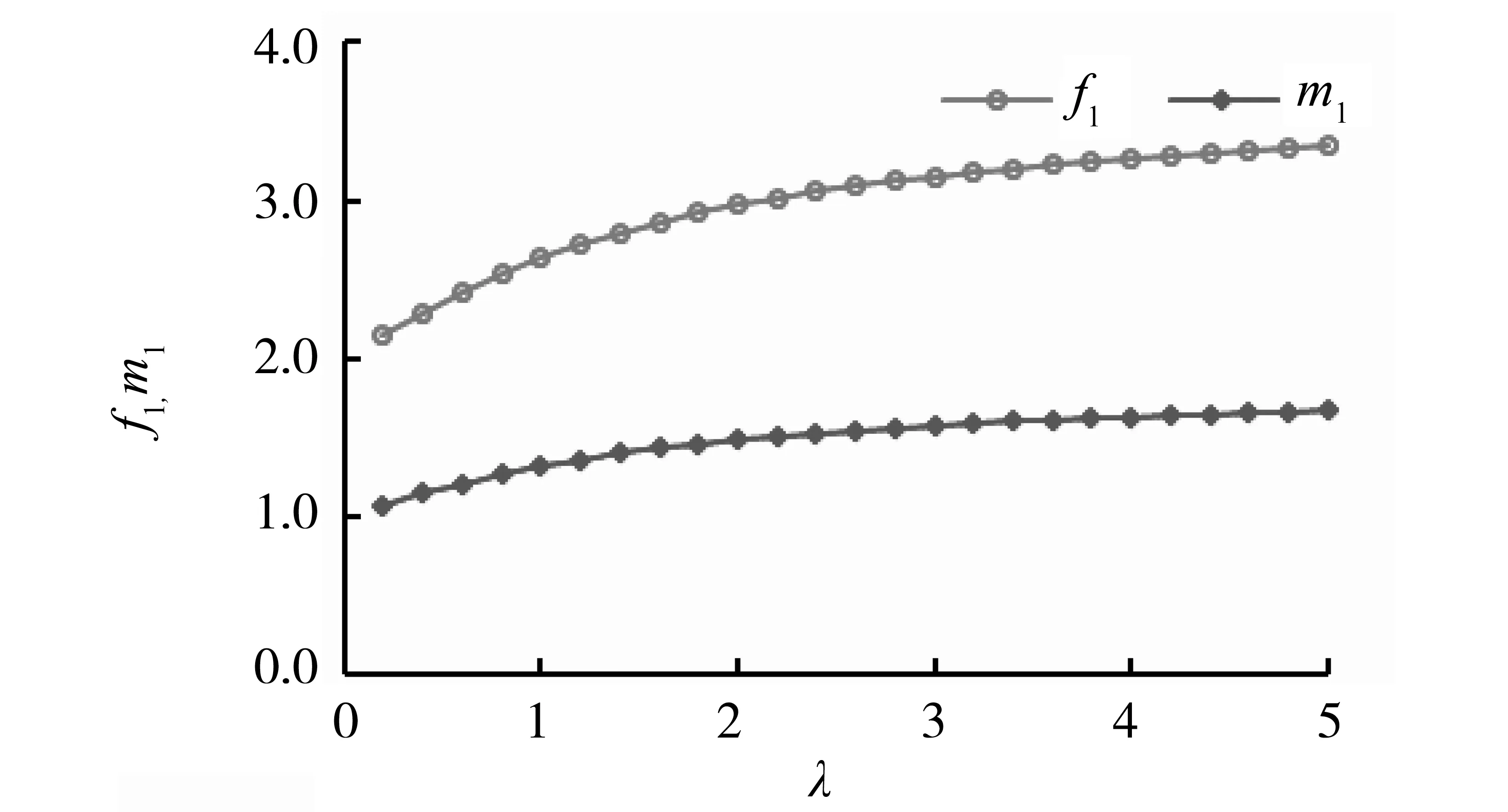
图2 最大无量纲水平波浪力和水平波浪力矩Fig.2 The maximum dimensionless horizontal wave force and moment
图3为Airy微幅波理论对防波堤单位长度最大无量纲波浪力和力矩的计算结果。按Airy微幅波理论算式[11],结果与入射角度大小无关。当kd取值较小时,即为微幅波理论在浅水条件下的计算值。将图3对应kd较小值的波浪力和力矩幅值与图2椭圆余弦波一阶分量理论计算结果相比较,可见椭圆余弦波理论所算结果明显大于微幅波理论的对应算值,由此说明在一定的浅水条件下,椭圆余弦波理论对波浪直接作用的预测更趋于合理可靠。

图3 Airy波理论计算的最大无量纲水平波浪力与力矩Fig.3 The maximum dimensionless horizontal wave force and moment given by Airy wave theory
图4和图5为海床综合特性系数不同取值下防波堤底部单位长最大无量纲浮托力及倾覆力矩随参数kb的变化结果,其中Cs=0对应海床不变形及孔隙水不可压缩情形。由图中可以看出,最大无量纲浮托力及倾覆力矩随kb呈单调递减趋势。在相同条件下随参数Cs的减小,浮托力幅值与倾覆力矩幅值均随之增大,当Cs=0时,浮托力和倾覆力矩幅值达至最大。据此,在随后针对其它不同参数对渗流载荷影响的计算中,均考虑Cs为零的情形。

图4 最大无量纲浮托力Fig.4 The maximum dimensionless uplift force

图5 最大无量纲倾覆力矩Fig.5 The maximum dimensionless overturning moment
图6和图7为不同入射波角度下防波堤底部单位长度最大无量纲浮托力和倾覆力矩随参数kb的变化结果。如图所示,斜入射浅水波的入射角度变化对防波堤底部的波浪渗流作用具有明显的影响。其中正入射(入射角为零)对应最大渗流载荷幅值,随着入射角的增大,浮托力和倾覆力矩幅值均随之减小,而减小的幅度随入射角增大随之降低。
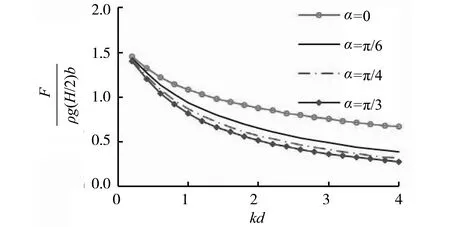
图6 最大无量纲浮托力Fig.6 The maximum dimensionless uplift force
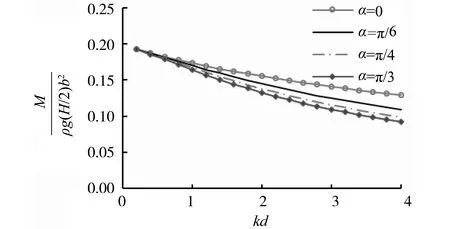
图7 最大无量纲倾覆力矩Fig.7 The maximum dimensionless overturning moment
图8和图9为防波堤堤宽和海床厚度之比不同取值下单位长度防波堤最大无量纲浮托力及倾覆力矩随参数kb的变化结果。如图所示,堤宽和海床厚度比的变化对无量纲浮托力幅值与倾覆力矩幅值的影响不大,相对而言,对倾覆力矩幅值更为明显一些。随着堤宽与海床厚度比的减小,渗流载荷幅值略为下降。
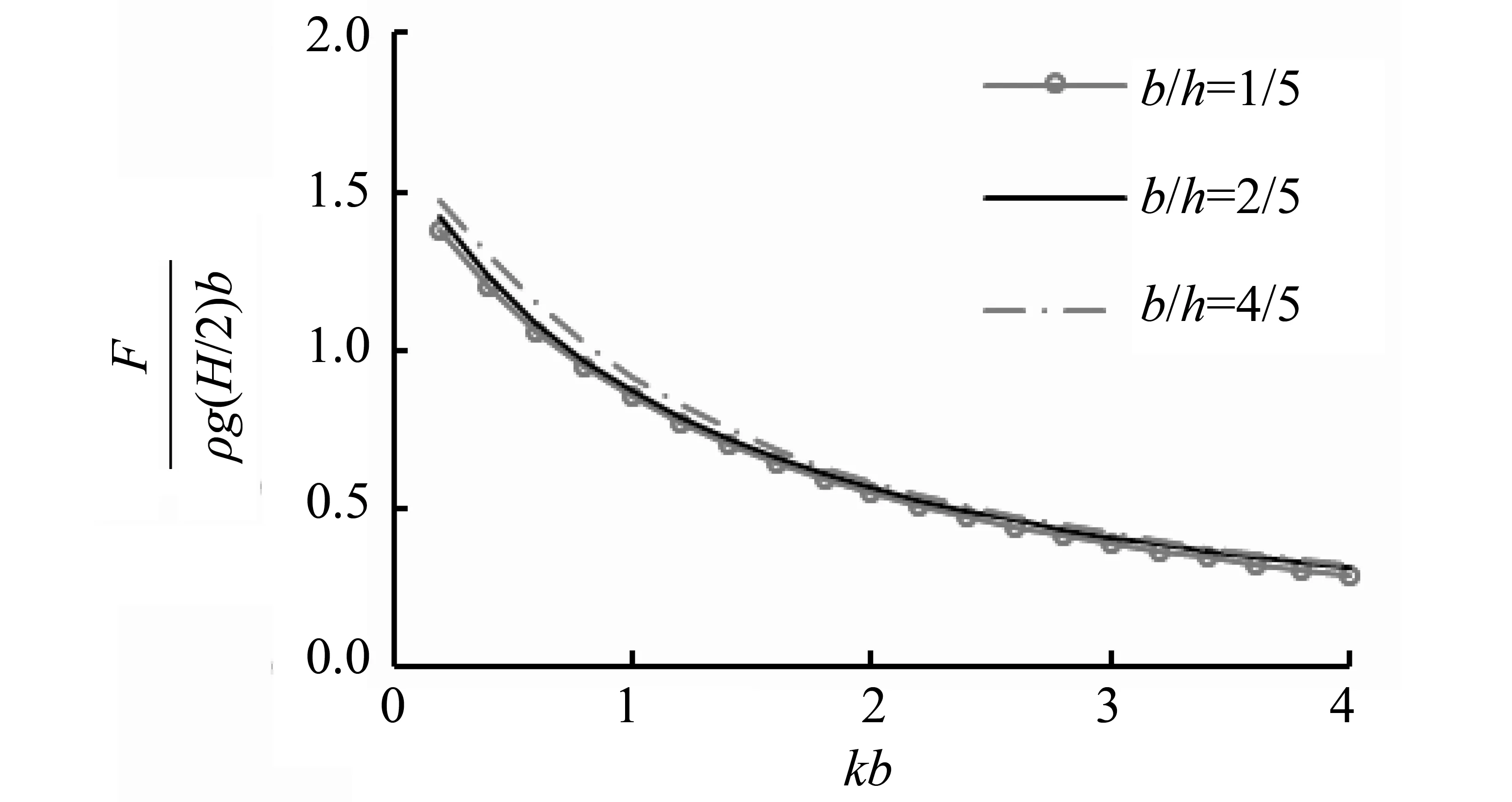
图8 最大无量纲浮托力Fig.8 The maximum dimensionless uplift force
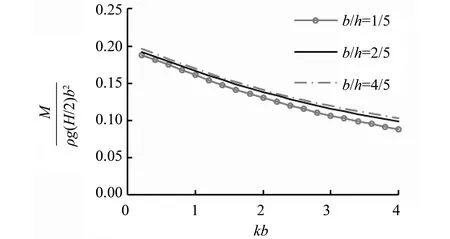
图9 最大无量纲倾覆力矩Fig.9 The maximum dimensionless overturning moment
图10与图11为椭圆余弦波理论与浅水条件下Airy微幅波理论所算单位长无量纲浮托力及倾覆力矩幅值的比较结果。如图所示,由椭圆余弦波一阶分量理论所算波浪渗流载荷结果明显大于浅水条件下微幅波理论的对应算值。由此说明在波浪渗流作用的计算中,相比Airy微幅波理论,椭圆余弦波理论同样更趋于合理可靠。此外,随着浅水波非线性特征参数λ的增加,无量纲浮托力及倾覆力矩幅值也随之有所增加,反映了浅水波非线性因素变化对波浪渗流作用具有一定影响。

图10 椭圆余弦波与Airy波对应的最大无量纲浮托力比较Fig.10 Comparison of dimensionless uplift force for cnoidal wave theory and Airy wave theory

图11 椭圆余弦波与Airy波对应的最大无量纲倾覆力矩比较Fig.11 Comparison of dimensionless overturning moment for cnoidal wave theory and Airy wave theory
图12和图13为防波堤单位长最大无量纲浮托力及倾覆力矩与水平波浪力及力矩的对比结果。结果表明:在一定条件下,浮托力及倾覆力矩幅值可以接近甚至超过水平波浪力及力矩幅值,由此说明在防波堤的实际工程设计中,对波浪引起的海床内渗流压力产生的对防波堤底部的渗流载荷也必须充分加以考虑。

图12 最大无量纲浮托力与水平波浪力比较Fig.12 Comparison between the maximum dimensionless wave force and uplift force

图13 最大无量纲倾覆力矩与水平波浪力矩比较Fig.13 Comparison between the maximum dimensionless wave moment and overturning moment
4 结 论
本文将椭圆余弦波一阶分量理论与Biot波浪渗流固结理论相结合,推广特征函数展开法,给出了复杂浅水波斜入射条件下固立于可渗透弹性海床上的直立防波堤的反射波浪场与波浪引起的海底下海床内渗流压力的解析解,从而对浅水条件下Airy波理论的波浪渗流作用的微幅波计算理论加以了有效地推广。通过对波浪直接作用和波浪渗流作用进行实算与比较,以及对椭圆余弦波理论与Airy波理论相应结果进行比较,揭示了斜入射椭圆余弦波引起的对防波堤底部的波浪渗流作用的各种变化规律。
计算结果表明,由椭圆余弦波一阶分量理论所算的防波堤单位长直接波浪载荷幅值和波浪渗流载荷幅值均明显大于由Airy微幅波理论所算结果,由此说明在浅水条件下的防波堤波载计算中,对应一定的海况条件采用椭圆余弦波理论较Airy微幅波理论更趋于合理可靠。此外,海床不变形及孔隙水不可压缩情形(Cs=0)对应的波浪渗流载荷最大,这与Airy微幅波理论所算结论基本一致。至如浅水波入射角度的变化对单位长防波堤水平波浪力(矩)幅值虽无影响,但对波浪引起的单位长防波堤渗流力(矩)幅值有明显影响,正入射浅水波将产生对防波堤底部的最大渗流作用。结果进一步表明浅水波非线性特征参数λ的变化对防波堤的渗流作用也具有一定影响,其中对渗流倾覆力矩的影响更为明显一些。通过对波浪直接载荷与波浪渗流载荷计算结果的对比,说明波浪渗流力(矩)幅值可能接近甚至超过水平波浪力(矩)幅值,表明在对波浪与防波堤相互作用问题的考虑中,波浪引起的渗流作用不容忽视。在防波堤实际设计中,采用椭圆余弦波浅水波模型预测波浪直接载荷以及波浪渗流载荷是可行合理和更为可靠的。
[1] 李玉成,滕斌. 波浪对海上建筑物的作用[M]. 北京:海洋出版社, 2002: 15-18.
[2] 邱大洪. 波浪渗流力学 [M]. 北京: 国防工业出版社, 2006: 193-203.
[3] 朱梦华,黄华,詹杰民,等. 斜入射水波对直立防波堤的波浪渗流作用[J].水运工程,2015,9(507):16-22.
[4] 邹志利,邱大洪. 直立式防波堤基底波浪渗流压力解析解[J]. 水动力学研究与进展, 1992,7(3):295-302.
[5] 倪寅,郑永来,钟佳玉. 多孔海床在波浪作用下渗流特性数值模拟[J]. 武汉工业学院学报, 2009, 28(3):55-58.
[6] 曾昭銮,黄华,詹杰民,等. 固立于可渗透弹性海床上透空型圆柱的波浪渗流力[J]. 中北大学学报(自然科学版), 2010,31(4):327-330.
[7] 黄华,曾昭銮,詹杰民,等.二层海中立于可渗透海床上的大直径墩柱的波浪渗流力[J]. 中山大学学报(自然科学版), 2011, 50(2): 36-41.
[8] 陈瑞志,黄华,詹杰民,等. 作用于透空复合圆柱的波浪渗流力的解析计算[J]. 中山大学学报(自然科学版), 2015, 54(3):1-9.
[9] 黄华,许潇楠,詹杰民,等. 作用于二层海洋中大直径透空圆环墩柱上的波浪渗流力[J]. 中山大学学报(自然科学版),2013,52(5):6-13.
[10] 李奇,黄华,詹杰民,等. 孤立波引起的对固立墩柱底部的波浪渗流作用[J]. 热带海洋学报,2013,32(5):42-47.
[11]ISSACSONMdeStQ.Shallowwavediffractionaroundlargecylinder[J].JournaloftheWaterway,Port,CoastalandOceanDivision,ASCE. 1977, 103:69-82.
[12] 朱梦华,黄华,詹杰民,等. 椭圆余弦波对透空直立防波堤波浪力解析计算[J].人民黄河, 2015,37(11):36-42.
[13] 邱大洪,贾影,减军. 椭圆余弦波与直墙的相互作用[J].水利学报, 1996(9):11-21.
[14] 徐云峰,夏小和,王建华,等. 椭圆余弦波作用下海床的响应[J].上海交通大学学报,2013,47(10):1580-1584.
[15] 李奇,黄华,詹杰民,等. 作用于透空圆环墩柱的浅水波绕射波浪力与波浪渗流力[J]. 中山大学学报(自然科学版),2013,52(3):23-29.
[16]SUMingde,PANYu.Atheoreticalinvestigationonthewaveforcesonthemultiplecylindersinshallowwater[J].AppliedMathematicsandMechanics,1987,8(4):377-387.
Oblique incidence cnoidal water wave-induced seepage effects on vertical breakwater
ZHUMenghua,HUANGHua,ZHANJiemin,ZHANGAo,GUOLin,CHENRuizhi
(Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China)
Based on cnoidal wave theory and expanding Biot consolidation theory, the mathematical solutions to the problems of oblique incidence shallow water wave reflected by vertical breakwater resting on permeable elastic seabed are given, and accordingly the analytical solutions to the shallow wave-induced seepage pressure are derived by applying the eigenfunction expansion approach. Then the wave-induced uplift force and overturning moment caused by the seepage pressure on the bottom of vertical breakwater are accordingly evaluated and compared with horizontal wave force and moment. The evaluating results demonstrate that in certain condition, the wave-induced seepage loads may have same order of magnitude as the direct wave loads. The variation of incident wave angle, sea water and seepage condition, and structure geometry condition may have some influence on wave-induced seepage loads, especially on wave-induced seepage overturning moment. The cnoidal wave-induced seepage loads are obviously larger than those predicted by Airy wave theory for shallow water, it denotes that the cnoidal wave theory can reflect wave nonlinear effects.
cnoidal wave; vertical breakwater; oblique incidence and reflection; permeable seabed; wave-induced seepage loads
10.13471/j.cnki.acta.snus.2016.04.007
2015-12-09
广东省协同创新与平台环境建设专项资助项目(2014B090904066);广东省公益研究与能力建设专项资助项目(2015A020216008)
朱梦华(1990年生),女;研究方向:水波动力学;通讯作者:黄华;E-mail:tsyhh1982@163.com
O
A
0529-6579(2016)04-0039-08
