自起动实心转子永磁电机性能分析计算与优化
2016-06-04姚丙雷陈伟华
张 健, 窦 娜, 程 源, 姚丙雷, 陈伟华
[1. 北京新能源汽车股份有限公司,北京 102606;2. 国核电力规划设计研究院,北京 100095;3. 山西长治供电公司,山西 长治 046000;4. 上海电器科学研究所(集团)有限公司,上海 200063]
自起动实心转子永磁电机性能分析计算与优化
张健1,窦娜2,程源3,姚丙雷4,陈伟华4
[1. 北京新能源汽车股份有限公司,北京102606;2. 国核电力规划设计研究院,北京100095;3. 山西长治供电公司,山西 长治046000;4. 上海电器科学研究所(集团)有限公司,上海200063]
摘要:针对现阶段单纯基于磁路法计算精度相对不高的问题,研究了磁路法和时步有限元法的优势和不足。以一台22kW实心转子永磁电机为例,分别采用两种方法计算了在空载情况下电机的气隙磁密、空载感应电势以及负载情况下的起动转矩、最小转矩等性能指标;并对该样机部分性能指标进行实测。对比实测与计算结果表明,有限元方法准确可靠。进而试算了在不同气隙大小及不同磁钢宽度时电机的性能,提出改进方案,为永磁电机的优化设计提供了重要参考。
关键词:自起动永磁电机; 磁路法; 时步有限元法; 优化设计
0引言
自起动实心转子永磁同步电动机(以下简称永磁电机)具有起动性能好、功率因数高、效率高、气隙磁密波形易于优化以及转子机械强度高等优点,在一些长期连续运行的场合替代传统的异步电机具有较大的节能优势,因此得到越来越广泛的应用[1-2]。
实心转子一般采用焊接加工,常见的实心转子电机结构中,一般气隙长度设计得较大,势必增加永磁体用量,加大起动电流倍数。文献[3]研究了气隙大小和永磁体厚度对转矩脉动的影响,最终确定了转矩脉动较小的气隙大小及永磁体宽度。文献[4]采用有限元法计算了实心转子永磁同步电动机在不同的气隙长度条件下的气隙磁密、空载反电动势、功率因数、效率和起动转矩等。为了得到合适的气隙磁密,并使漏磁系数保持在适宜值,还要考虑到尽可能减少永磁体的用量。这需要在保证性能的前提下,合理地选择永磁体厚度,以降低电机的制造成本[5]。
传统的基于磁路的电机设计方法,简单快捷,具备一定的设计精度,至今仍是电机领域实际工程的主要设计方法之一。但是,现有的基于磁路法的永磁电机模型无法准确计算谐波分布、起动特性等,而以时步有限元为代表的数值解法,可以得到很高精度的数值解。本文分别采用磁路法与时步有限元法对一台22kW实心转子永磁电机进行计算,分析了永磁电机在不同的永磁体厚度及气隙大小下对气隙磁密、空载感应电势及转矩等的影响,通过对比,得出使永磁电机性能指标较好的永磁体尺寸及气隙大小。根据计算结果对该样机提出改进方案。
1永磁电机性能计算方法
1.1磁路法
基于磁路法的电机计算程序能以很快的速度计算出电机的总体性能,具备一定的设计精度。尽管基于磁路的计算方法在异步电机、较大型的同步电机分析中,可以得到较为满意的精度,但对于结构复杂的永磁电机,特别是小型永磁电机的分析,磁路不均匀且存在着多种饱和与非线性因素,会引入较大的计算误差,所以采用有限元方法就十分必要,特别是在研究永磁电机的起动过程[1-2]。
1.2有限元方法
文献[6-7]对场-路与定转子间动动直接耦合的时步有限元法做了详细介绍。该方法将整个计算过程划分为若干个时步,每个时步计算完成之后,使用重剖分法处理发生相对运动的气隙层,建立了以转子端环电流为状态变量的转子回路方程,通过求解方程得到相应的变量。该计算模型基于如下假定条件[7]:
(1) 使用2D平面场仿真3D场,端部电感电阻等参数以由磁路法计算得到的集中参数确定;
(2) 永磁体材料忽略其磁滞效应,由给定的BH曲线确定其特性,忽略温度变化对永磁体剩磁的影响;
(3) 激励源是理想三相电压源,忽略线路阻抗的影响。
电机内电磁场瞬态边值问题如式(1)所示:
(1)
式中: Ω——求解区域;
Γ1——磁场的边界,定子外圆和转子内圆的边界,此边界以外区域无磁场分布;
Γ2——永磁材料与铁心的交界线,该线上将被赋以电流用来模拟永磁磁场,该电流的电流密度由δs表示;
μ——求解区域内各材料的磁导率。
由于永磁电机三次谐波磁场以及感生的三次电势的存在,永磁电机多用星接方式接线,在考虑因饱和与谐波效应等因素可能导致的三相电流不对称的情况,列定子电路方程如式(2)所示。
(2)
式中: r——定子绕组的相电阻;
Ls——定子端部漏抗;
e——感应电势。
考虑电机的机械运动方程的转子方程如下:
(3)
式中: Te——气隙电磁转矩;
Jm——系统的总体转动惯量,包括转子自身的转动惯量和负载的转动惯量;
Ωm——机械角速度;
Tm——负载转矩;
θm——转子转过的机械角度。
将方程组(1)~(3)联立,即可完整地表达永磁电机总体方程,具体表达式以及求解方法,可参见文献[7]介绍,在此不再赘述。
2永磁电机性能计算与测试
该样机整体结构截面局部视图如图1所示。
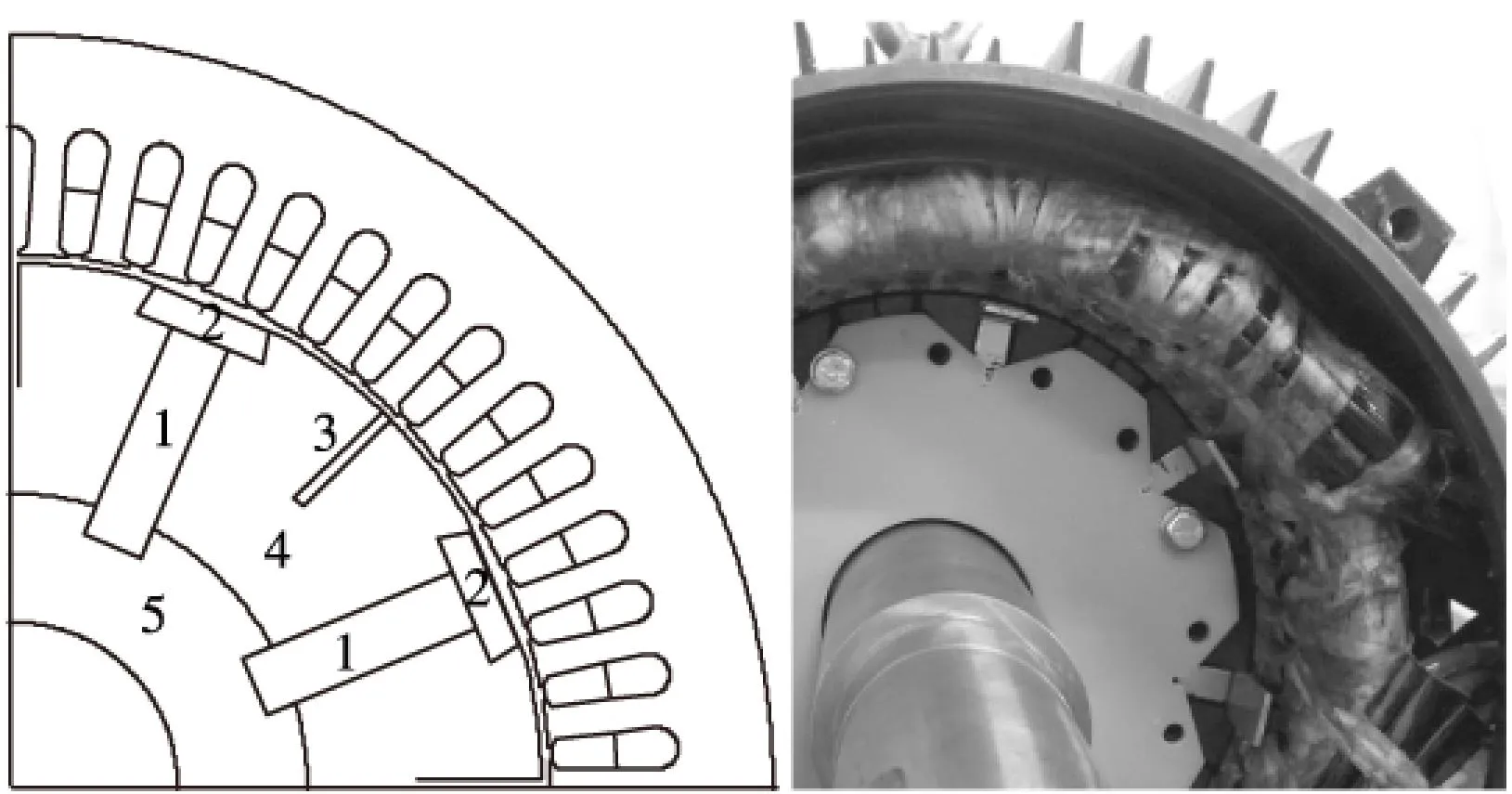
图1 样机截面局部视图
在图1中: 1—永磁体,一对极下均只有一块永磁体,按切向磁化方向布置;2—起动导条,兼起到槽楔的作用,端部使用铝板连接,该导条为燕尾形结构,上下底边长分别为13mm和17mm,厚8mm;3—小槽铜板,与端环焊接,宽1.5mm,长20mm;4—由实心钢做成的转子铁心,可以根据需要将表面加工成不同的形状,达到优化气隙磁密的效果;5—不锈钢轴套,内径40mm,外径80mm,除了起动焊接固定磁极的作用以外,还起到隔磁作用,得到较小的漏磁系数。表(1)列出了样机的其他关键参数。
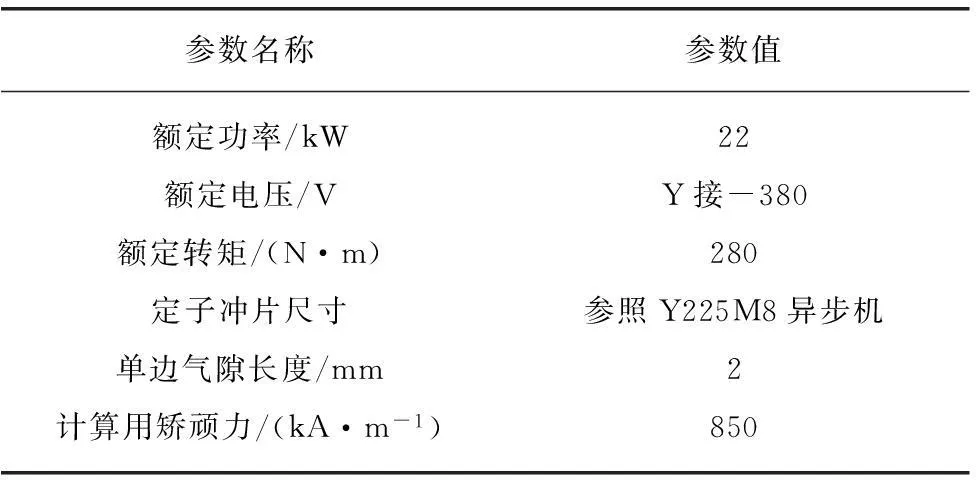
表1 样机关键参数
2.1基于“路”的永磁电机性能计算
首先使用Ansoft软件中采用磁路法计算的RMxprt模块对该样机进行空载起动计算[8],其性能如图2所示。
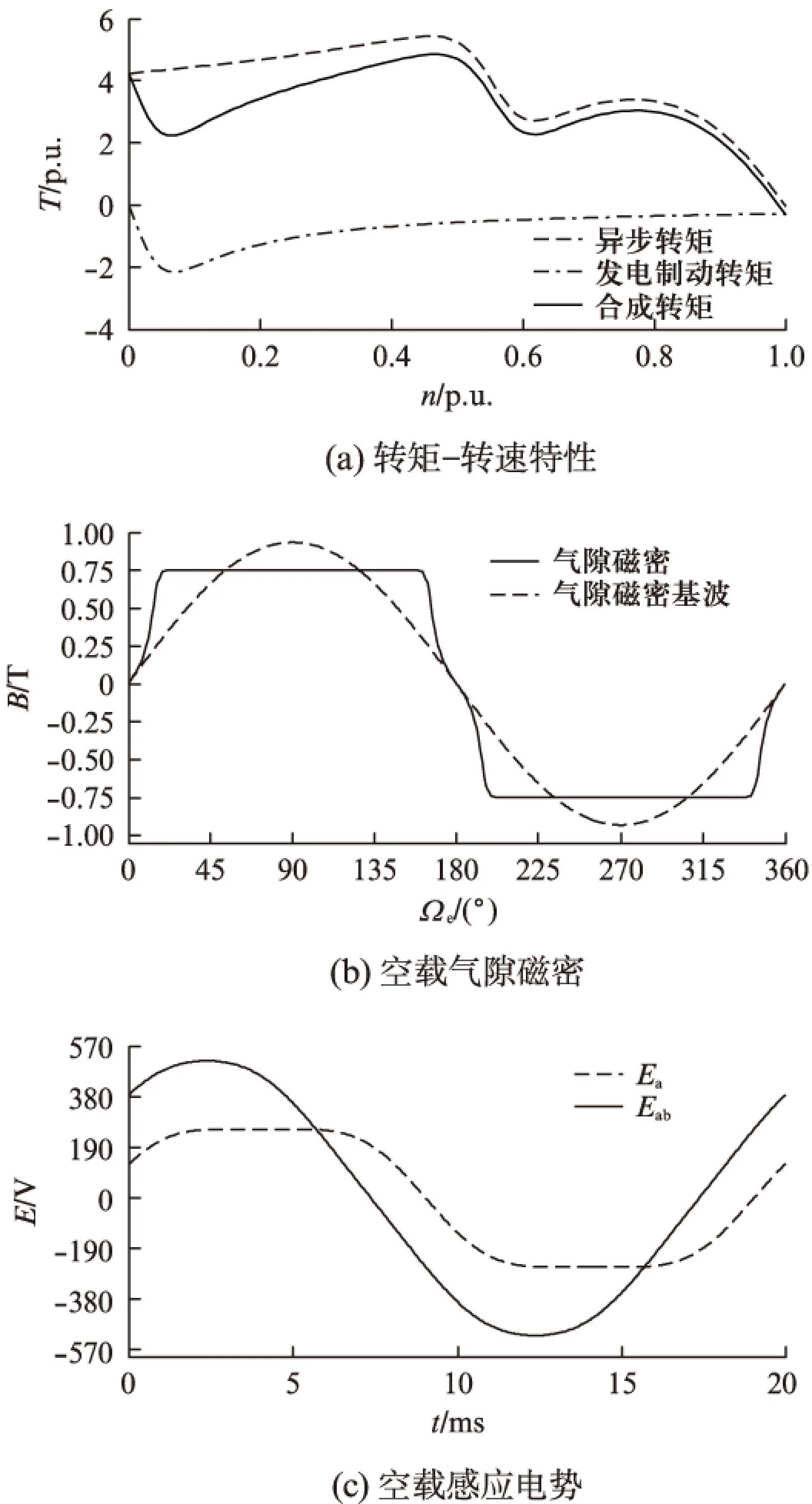
图2 永磁电机磁路计算结果
由图2可知,使用磁路法计算得到的堵转转矩约为4.26倍额定转矩,最小转矩约为2.26倍额定转矩;空载气隙磁密呈现平顶波形,平均磁密为0.655T,基波磁密最大值为0.935T;空载感应相电势亦呈现平顶波形,而线电势则接近于正弦波,且基波有效值为370.7V。
虽然磁路法计算速度快、方便调整结构尺寸等诸多优点,但也存在着设计结构选择空间较小,不适用于复杂磁路结构,无法准确考虑饱和非线性等诸多不足。因此在使用磁路计算得到总体性能的基础上,再用有限元方法详细分析其电磁性能。
2.2基于“场”的永磁电机性能计算
永磁电机的转矩转速特性曲线(T-n)基于“场”的计算与磁路法相比有较大不同,文献[9-10]介绍了一种以似稳态法分别在不同转速下计算转矩的方法。该方法可以较为准确地计算出T-n曲线,但耗时极长;同时该文献还介绍了一种基于数据处理方法求取T-n曲线的方法,本文利用该方法计算了样机起动过程T-n曲线,如图3(a)所示。
空载气隙磁密的计算,是指计算得到在定子绕组开路情况下气隙磁密的法向分量Bn,由有限元计算时得到的是各节点的矢量磁位Az利用式(4)即可得到Bn,如图3(b)所示。
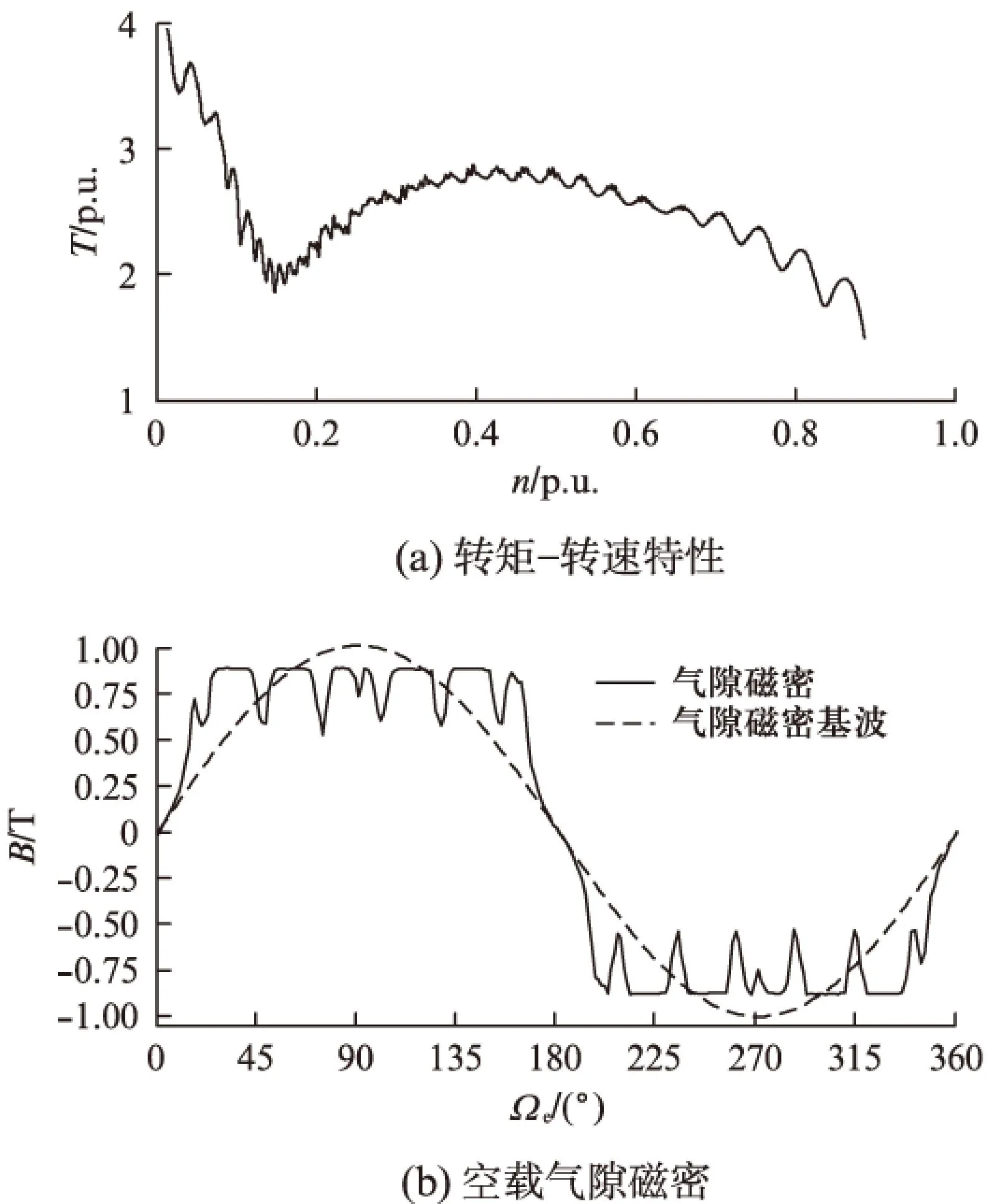
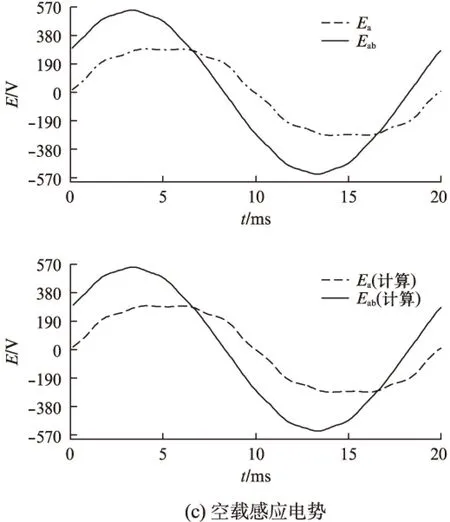
图3 永磁电机时步有限元计算结果
(4)
空载感应电势,是由有限元计算得到的节点矢量磁位Az利用式(5)计算得[7]:
(5)
其中: K是一个总体系数矩阵,由绕组不同方式等多因素共同决定,对于每一种绕组连接方式,都是一个固定的矩阵;Δe是每个单元的面积;np表示绕组线圈边即导流区域所包含的单元总数;Ai、Aj、Am则表示三角形单元的三个节点的矢量磁位(对于2D场来说,是矢量磁位的Z轴分量,一般称用Az表示)。以照前述的时步法有限元计算过程,通过对时间进行离散,可以求得其感应电势波形,如图3(c)所示。
由图3可知,该电机的堵转转矩(起动转矩)平均值约为3.98倍额定转矩,最小转矩约为1.97倍额定转矩;空载气隙磁密平均值0.687,基波磁密最大值为0.983T;空载感应相电势接近平顶波形,而线电势接近于正弦波,且基波有效值为385.6V。
对比图2和图3发现,采用“路”与“场”两种方法计算出的空载气隙磁密基波相近,但磁场计算时得到了磁路法无法得到因定转子开槽所引起的齿谐波。
2.3样机实测
为了检验计算结果,利用实验室永磁电机综合测试平台[11]对样机进行了测试。本测试平台使用一套高性能DAQ设备,由美国NI公司同步数据采集卡、LEM公司霍尔型电流传感器、Kistler公司双量程转矩传感器,配合LabVIEW编程组成。该平台既可以测试常规的稳态运行工况下的运行特性,还可以实时测试记录电机起动过程中的动态转矩转速以及电压电流波形。首先,测试空载感应电势波形,如图4(a)所示。其次,对样机进行负载起动测试,在永磁电机起动过程中,电磁转矩是一个急剧波动的动态转矩,无法直接从曲线上读取指标性转矩值,需要对曲线进行相应的处理[9]。当以50Hz工频电源对永磁电机进行直接起动时,可以近似地取20ms时间区间进行平均处理,在转速较低的阶段也具有一定的精度。起动过程转矩如图4(b)所示。
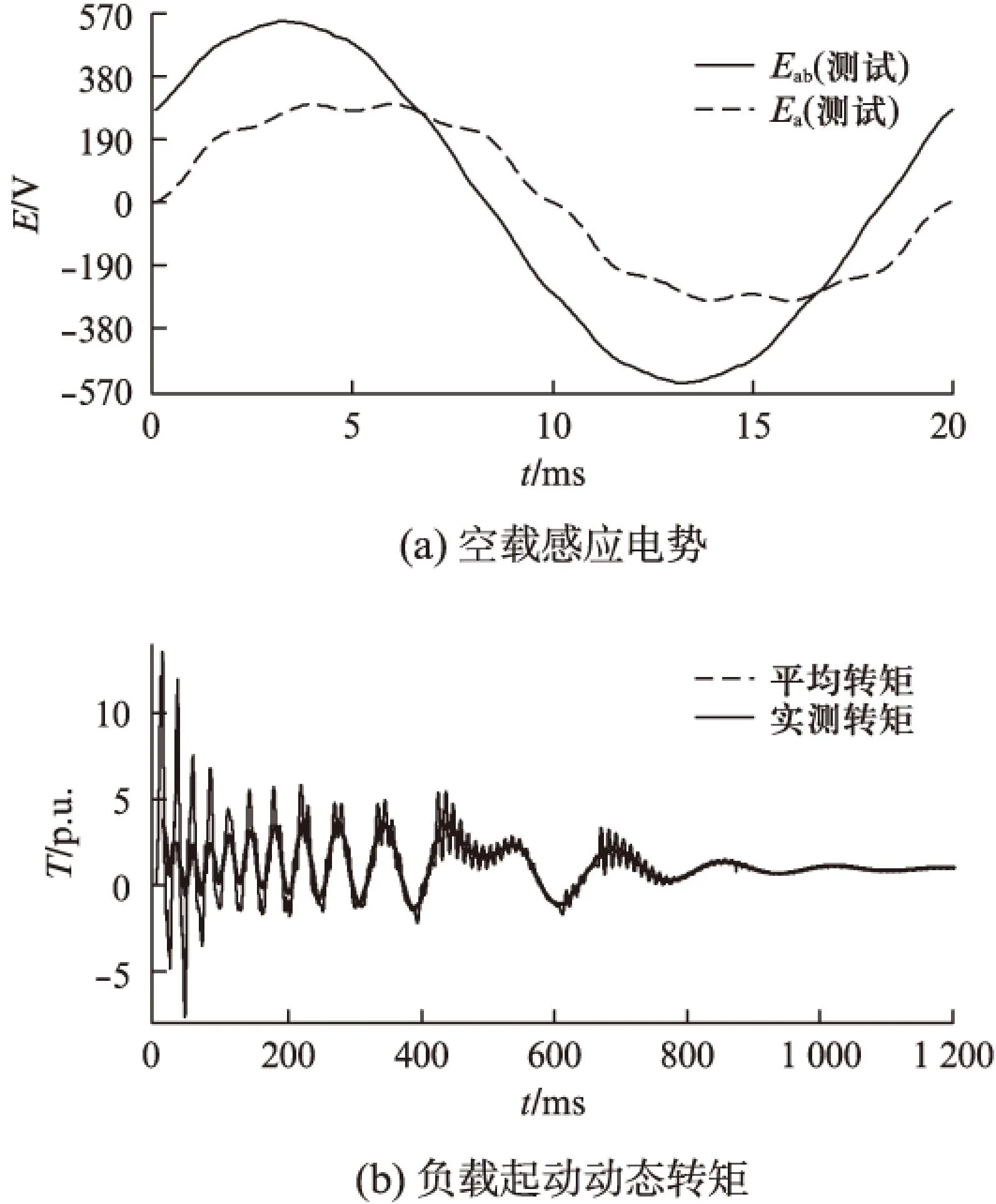
图4 样机实测结果
由图4可知,该样机的空载感应电势基波有效值为383.1V,起动转矩约为3.86倍额定转矩。
3计算与测试结果对比分析
将两种计算结果及实际测试结果对比如表2所示。表2中,Bav为气隙平均磁密,B1m指气隙磁密基波最大值;E0为空载感应线电势的有效值;Tst、Tmin均为标幺值,基值为电机的额定转矩280N·m。
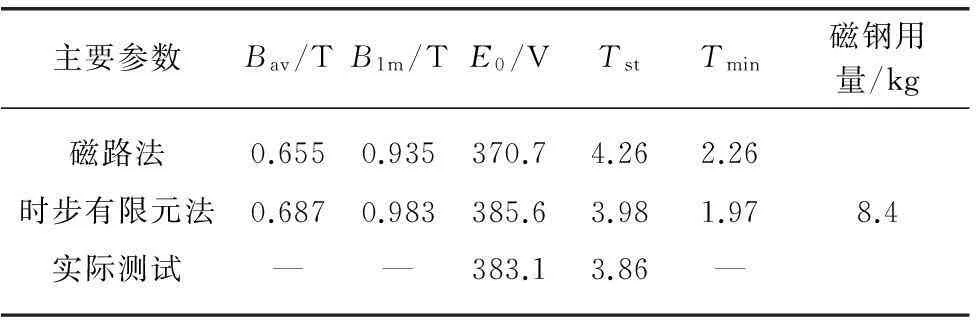
表2 计算及测试结果对比
注: 气隙2.0mm磁钢宽13mm。
受测试条件限制,气隙磁密波形难以测试,最小转矩的测试,需要在较低转速下给样机加载较大转矩,同样存在一定困难。现仅就空载时部分起动指标以实测数据为基准进行对比。空载感应电势计算结果,磁路法偏差为3.2%,有限元法偏差为0.6%;起动转矩计算结果,磁路法计算偏差为10.4%,有限元法偏差3.1%,说明时步有限元计算比较可靠。
4样机局部尺寸调整计算
为了验证该样机是否合理,能否以更低的成本达到较好的性能,以实际样机尺寸为基础,通过协调调整气隙大小和磁钢宽度,分别计算了不同的改进方案。计算结果见表3~4。
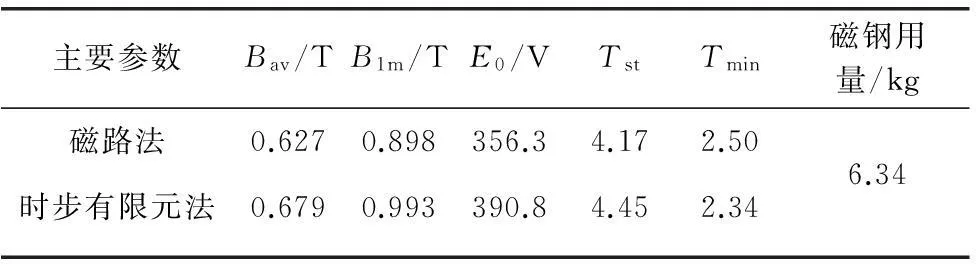
表3 尺寸调整方案1性能计算
注: 气隙1.5mm磁钢宽10mm。
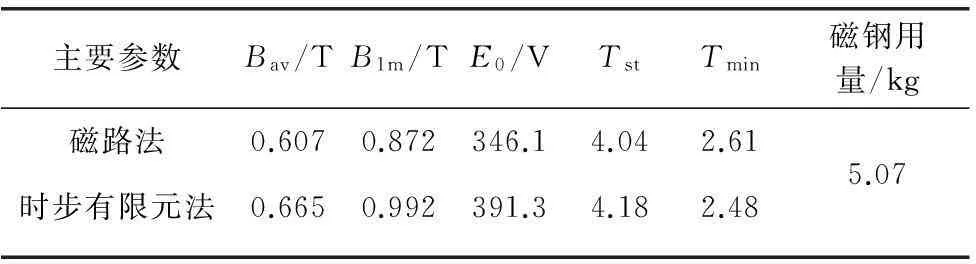
表4 尺寸调整方案2性能计算
注: 气隙1.2mm磁钢宽8mm。
表3、表4与表2中各项符号意义相同。对比表2~4发现,在表2所对应的结构中由于磁钢较厚、气隙较大,在起动过程中起动转矩较大,但最小转矩较小。随着气隙的减小,磁钢用量减少,起动转矩增大,最小转矩则大大增加。较大的最小转矩有利于提高电机在大转动惯量、重负载条件下的起动能力。由分析可知,表3所对应的模型方案是一种比较经济适用的方案。
5结语
在常用的自起动永磁电机性能计算方法方面,首先对比分析了磁路法和时步有限元法的优势及不足,并分别使用磁路法和有限元法计算了一台样机的性能。对样机部分性能指标进行实测,将实测结果与计算结果作对比分析,说明采用有限元方法计算是比较可靠的。最后试算了在不同气隙大小以及不同磁钢宽度时电机的性能,提出了改进方案,为永磁电机的优化设计提供了重要参考。
【参 考 文 献】
[1]唐任远.现代永磁电机理论与设计[M].北京: 机械工业出版社,1997.
[2]GIERAS J F, WING M. Permanent magnet motor technology-design and applications[M]. New York: Marcel Dekker INC., 2002.
[3]王晓远,马涛.永磁体和气隙对双凸极永磁电动机转矩脉动的影响[J].微电机,2007,40(8): 26-30.
[4]乔鸣忠,张晓锋.实心转子永磁同步电动机气隙长度与性能研究[J].微特电机,2008(4): 12-14.
[5]王鑫,李伟力,程树康,等.实心转子永磁同步电动机起动性能[J].电机与控制学报,2007,11(4): 349-353.
[6]李志强.自起动永磁电机动态过程的有限元分析与实验研究[D].北京: 华北电力大学,2009.
[7]胡敏强,黄学良.电机运行性能数值计算方法及其应用[M].南京: 东南大学出版社,2003.
[8]赵博.Ansoft12在工程电磁场中的应用[M].北京: 中国水利水电出版社,2010.
[9]张健,罗应立,陈伟华,等.自起动永磁电机最小转矩的时步有限元计算[J].电机与控制学报,2011,15(3): 80-85.
[10]张健.永磁电机性能及参数数值计算与实验研究[D].北京: 华北电力大学,2012.
[11]李志强,曹彦朝,张健,等.永磁电机微机综合测试系统[J].电机与控制应用,2009,36(3): 57-61.
引领技术发展趋势报道经典实用案例反映行业最新动态
Solid Rotor Line-Start Interior Permanent Magnet Synchronous Motor Optimal Design
ZHANGJian1,DOUNa2,CHENGYuan3,YAOBinglei4,CHENWeihua4
(1. Beijing Electric Vehicle Co., Ltd., Beijing 102606, China;2. State Nuclear Electric Power Planning Design & Research Institute,Beijing 100095, China;3. Changzhi Power Supply Company of Shanxi Province, Changzhi 046000, China;4. Shanghai Electrical Apparatus Research Institute(Group) Co.,Ltd.,Shanghai 200063, China;)
Abstract:To determine the no-load parameters and the starting-up capability of a Line-start Permanent-magnet Synchronous Motor (LSPMSM) are the fundamentals of a motor optimization design process. It was commonly recognized that the magnetic circuit method had a lower accuracy compared to FEA method, the advantages and disadvantages of the two methods were all analyzed taking a 22kW LSPMSM as an example. The two methods were applied to analysis the no-load air-gap flux density, back-EMF, starting-up torque and the minimum torque during the starting-up process. It was confirmed that the FEA method had a sufficient accuracy by comparing the test results and the analyzed ones. And then, the FEA method was used to optimize the air-gap length and the width of magnet, a new topology was worked out having better performance. The analysis method and the analyzed results could be treated as important references for a further optimization design.
Key words:line-start permanent magnet motor; magnetic circuit method; time-stepping FEM; optimal design
收稿日期:2015-09-06
中图分类号:TM 351
文献标志码:A
文章编号:1673-6540(2016)04- 0066- 05
作者简介:张健(1983—),男,工程师,研究方向为电动汽车驱动电机设计与性能评估。
