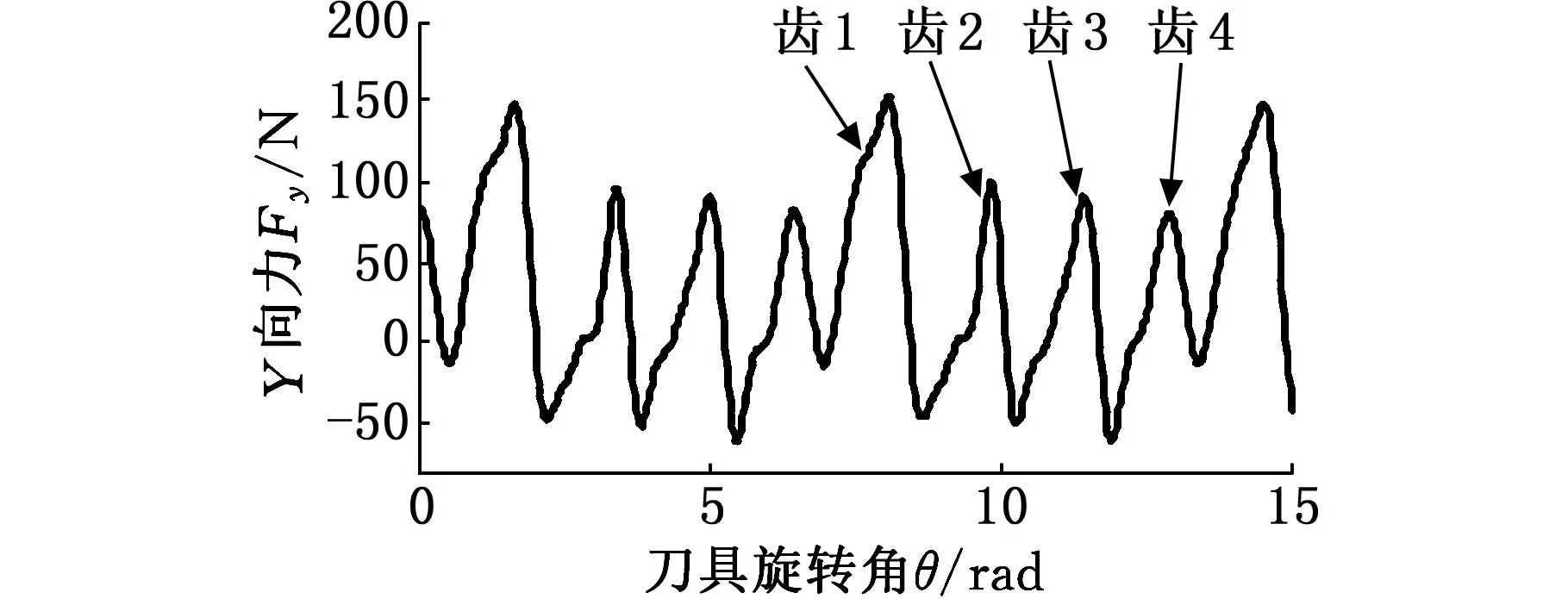
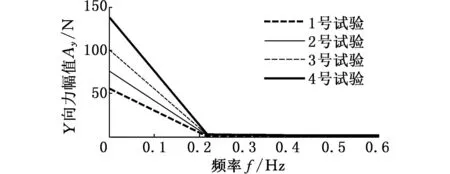
平底立铣刀在多刃切削时的切削力变化规律研究

刘　璨　吴敬权　刘焕牢　谭光宇

广东海洋大学，湛江，524088



平底立铣刀在多刃切削时的切削力变化规律研究

刘璨吴敬权刘焕牢谭光宇

广东海洋大学，湛江，524088

摘要：为揭示平底立铣刀在多刃铣削时的切削力变化规律，理论推导了多刃切削的水平方向公称切削力的数学表达式，发现这些公称切削力是旋转角的简谐函数，其常数项与同时参与切削的刃数成正比。将切削力表达式的系数做归一化处理，采用仿真方法，得到各常用齿数平底立铣刀在单刃、多刃连续切削时的公称切削力量纲一均值和刀齿频率幅值，结果表明：切削宽度方向的公称切削力均值在多刃切削时显著增大，而其刀齿频率幅值在多刃切削时有时增大，有时减小。开展了4齿平底立铣刀的切削测力试验，试验结果与理论推导和仿真结果相符。研究结果表明：与单刃连续切削相比，多刃切削的切削宽度方向的静态切削力显著增大；多刃切削在水平方向存在着更平稳和更不平稳两种可能；偶数齿铣刀的多刃切削最平稳。研究结论可为铣削加工中优选浸入角参数提供参考。

关键词：立铣刀；多刃切削；切削力；平稳；浸入角

0引言

立铣刀通常有多个刀齿，瞬时切削的刀刃数与铣刀齿数和浸入角相关。

令铣刀的齿数为z，浸入角为β。在立铣刀切削时，若β小于2π/z，则立铣刀不同刀刃的切削在时间上不连贯，为断续切削，在每个切削刃切入或切出工件时，切削力在最大值和0之间的过渡时间很短，对工艺系统的冲击较大。

在立铣刀连续切削时，若β等于2π/z，则在任意瞬时只有单个刀刃参与切削；若β等于2nπ/z (n为正整数，且n≥2)，则在整个切削过程中参与切削的刃数不变；若β的值介于2π/z和2nπ/z之间，则在整个切削过程中参与切削的刃数将交替变化。例如，4齿立铣刀在浸入角为π时为两刃连续切削，而当浸入角介于π/2和π之间时为两刃-单刃交替切削。

多刃同时参与切削可提高加工效率，但多刃切削力和单刃切削力可能有较大差异。Bobrenkov等[1]认为铣削力的高频成分的强度随同时参与切削的刀齿数增多而减弱。Kim等[2]进行了6齿面铣刀的切削力仿真，仿真结果显示，两刃-单齿交替切削时的切削力峰峰值大于单刃断续切削时的切削力峰峰值。Hwang等[3]进行了某种工况下的面铣刀在两刃和单刃切削时的切削力仿真，仿真结果显示，两刃切削时水平方向的切削合力均值和切削宽度方向的切削力峰峰值均比单刃切削时的大，而进给方向的切削力峰峰值比单刃切削时的小。李沪曾等[4]发现工艺系统的自激振动在端铣刀多刃切削时可能增强。袁平[5]发现，在3齿直刃立铣刀全宽槽铣时，进给方向的切削力比单刃铣削时有所减小，4齿立铣刀的水平方向的公称切削力表达式为常数，但他只以某些多刃切削特例为研究对象，没有探索多刃切削的通用切削力特征。

切削力对加工表面误差有重要影响[6]，而多刃切削力的变化规律尚有很多不清晰之处，本研究拟以刃数不变的多刃连续切削为对象，探索其与单刃连续切削两者的切削力差异。为便于阐述，下文所述单刃切削均指单刃连续切削，多刃切削均指刃数不变的多刃连续切削。

1理论推导

1.1单刃切削的切削力数学表达式

以逆铣为例，刀具和工件的平面几何关系如图1所示，点O为刀具轴心线；β为刀具浸入角；刀刃按顺时针方向排序，θi为第i 刃的旋转角；FR(θi)、FT(θi)分别为旋转角为θi时第i刃施加于工件的瞬时径向力和切向力。在笛卡儿坐标系中，切削力可分解为X、Y两个水平方向的分力和轴向分力，文献[7-9]的实测切削力数据都显示轴向切削力远小于水平方向切削力。本研究仅以水平方向切削力为对象。

令X和Y向的正方向如图1所示。若忽略刀具螺旋角的影响，则第i刃施加于工件的水平方向分力为

图1　立铣刀逆铣示意图

(1)

Fiy(θi)=-FR(θi)cosθi+FT(θi)sinθi

(2)

FR(θi)=KRazh(θi)

(3)

FT(θi)=KTazh(θi)

(4)

h(θi)=hN(θi)+hE(θi)

(5)

其中，Fix(θi) 、Fiy(θi)分别为第i刃施加于工件的X向力和Y向力；KR、KT分别为径向力和切向力的系数；az为切削深度；h(θi)为切削厚度；hN(θi)、hE(θi)分别为公称切削厚度和刀具偏心导致的切削厚度增量。

按照Tlusty等[10]的理论，公称切削厚度的计算公式为

hN(θi)=ftsinθi

(6)

式中，ft为每齿进给量。

按照刘璨等[11]的推导，刀具偏心导致的切削厚度增量的计算公式为

(7)

式中，ρ、α分别为刀具的偏心距和偏心角；z为刀具的刀刃数。

将式(3)～式(7)代入式(1)、式(2)得

Fix(θi)=FixN(θi)+FixE(θi)

(8)

Fiy(θi)=FiyN(θi)+FiyE(θi)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

式中，FixN(θi)、FiyN(θi)分别为第i刃施加于工件的X向和Y向公称力；FixE(θi)、FiyE(θi)分别为第i刃施加于工件的X向和Y向偏心力。

对于确定的刀具与工件组合，在每齿进给量ft和切削深度az不变的情况下，系数Kftaz/2为常数，将其归一化为1。同理，同一把刀具的刀齿数和偏心尺寸可视为常数，若切削过程中不换刀具，则系数2Kρazsin(π/z)也为常数，将其归一化为1。则式(10)～式(13)可写为

FixN(θ)=sinφ+sin(2θi-φ)

(16)

(17)

FiyN(θi)=cosφ-cos(2θi-φ)

(18)

(19)

1.2多刃切削的公称切削分力数学表达式

1.2.1数学表达式推导

由式(16)、式(18)可知，参与切削的第i+j个刀刃施加于工件的X向、Y向公称切削力表达式为

F(i+j)xN(θi)=sinφ+sin(2θ(i+j)-φ)

(20)

F(i+j)yN(θi)=cosφ-cos(2θ(i+j)-φ)

(21)

(22)

式中，θj、F(i+j)xN(θj)、F(i+j)yN(θj)分别为参与切削的第i+j个刀刃的刀具旋转角、X向公称切削力和Y向公称切削力。

令同时参与切削工件材料的刀刃数为m，则多刃切削时工件所受水平方向公称切削分力为

msinφ+ANsin(2θi-φ+γN)

(23)

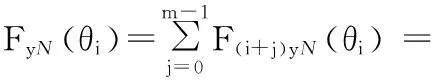
mcosφ-ANcos(2θi-φ+γN)

(24)

式中，FxN(θi)、FyN(θi)分别为多刃切削时工件所受X向、Y向公称切削力；AN、γN分别为表达式中简谐函数的系数和相位。

1.2.2数学表达式分析

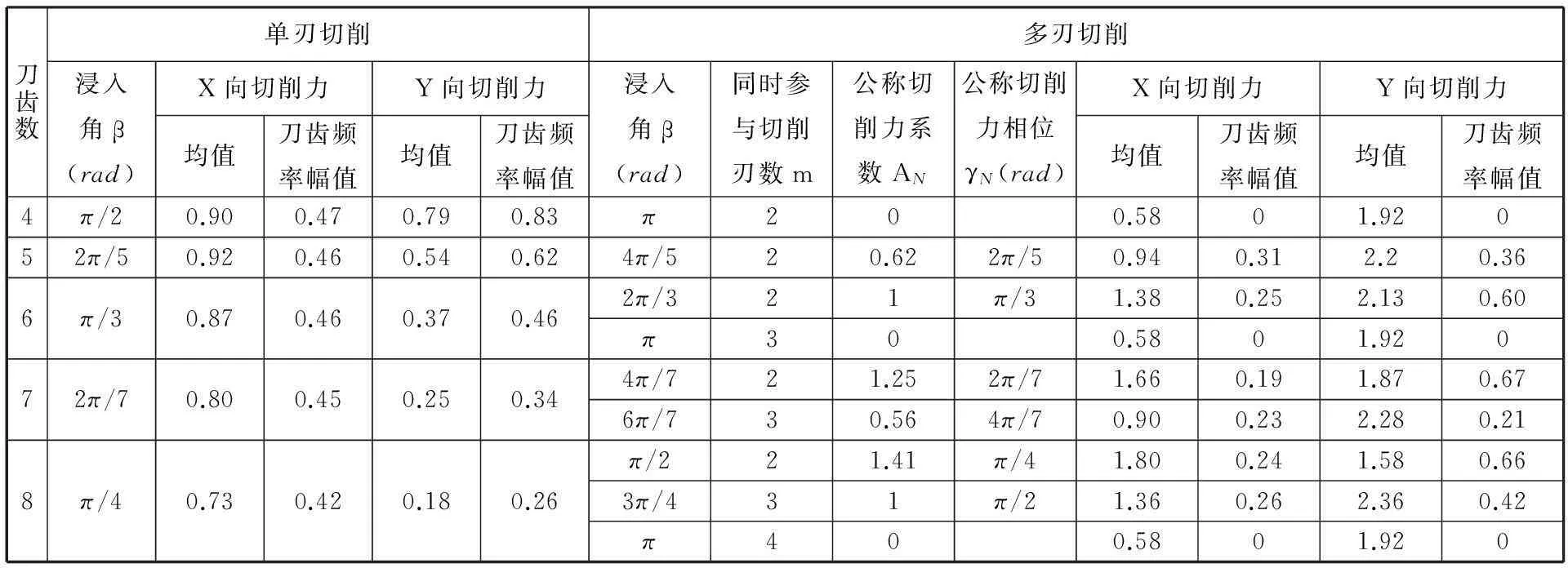
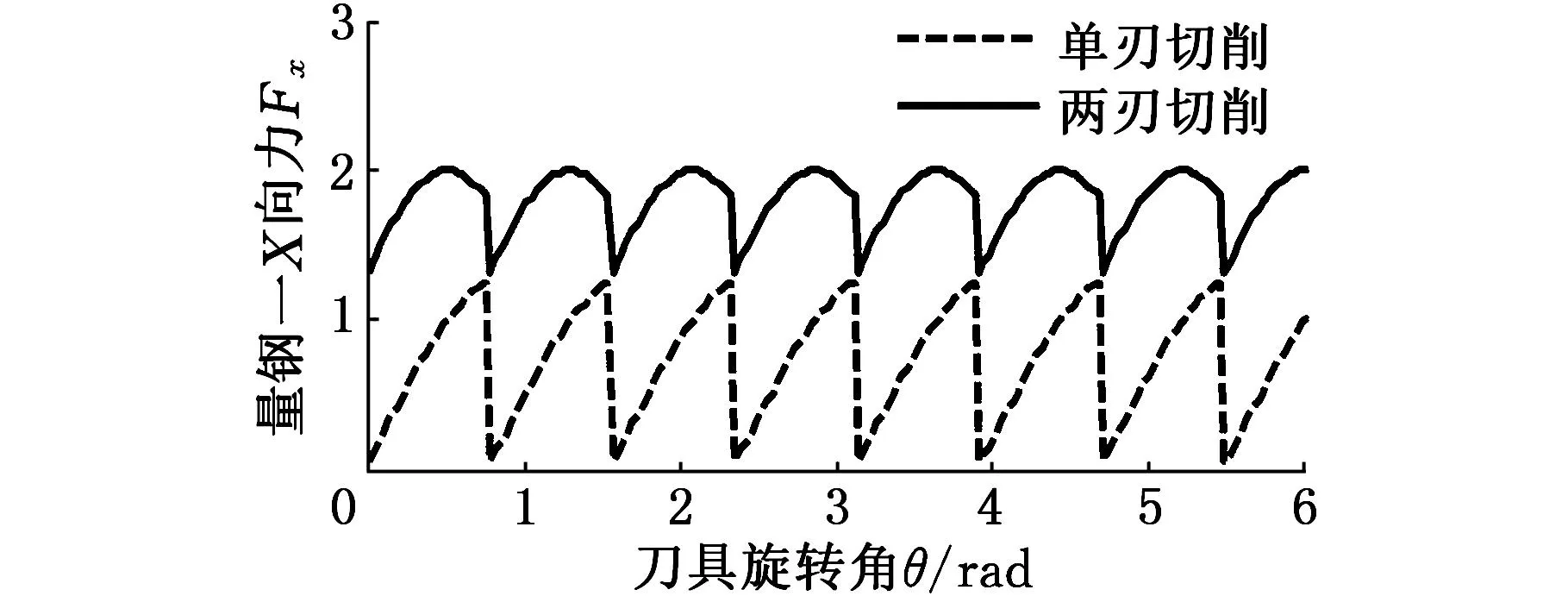
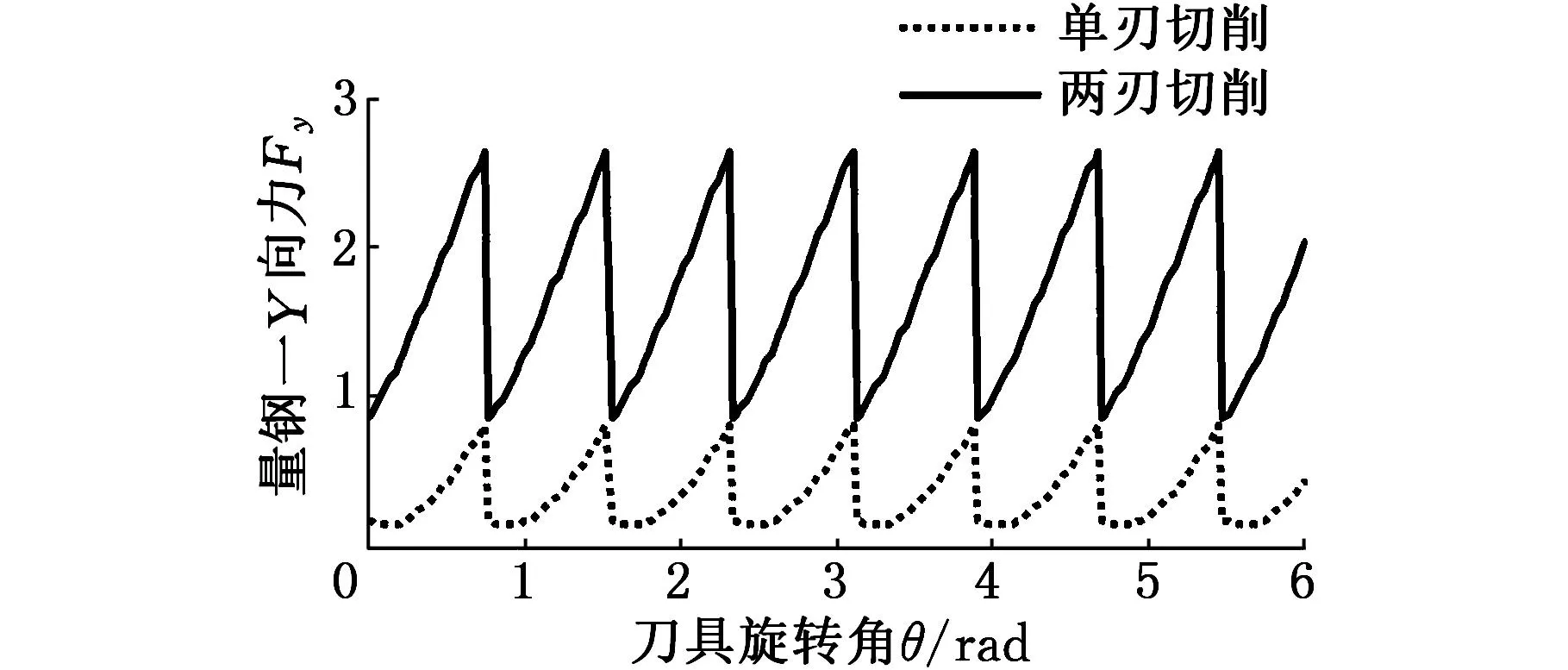
在刀具和工件确定后，φ的值将保持不变，则由式(16)、式(18)、式(23)、式(24)可见：①多刃切削的水平方向公称切削分力FxN(θi)、FyN(θi)与单刃切削的水平方向公称切削分力FixN(θi)、FiyN(θi)为相同频率的简谐函数，但两者的简谐函数系数和相位可能不同；②多刃切削时水平方向公称切削分力的常数项msinφ、mcosφ与同时参与切削的刃数m成正比；③由于tanφ小于1(如Janez等[12]、Engin等[13]研究得出tanφ约为0.3)，因此，sinφ

1.2.3多刃切削力数学表达式的参数推导

同时参与切削的刃数m与铣刀齿数z、浸入角β相关，本研究根据式(23)式、式(24)进一步做数学推导，确定各常用齿数平底立铣刀的FxN(θi)、FyN(θi)的具体表达式。

例如，对于6齿平底立铣刀，在2刃同时参与切削时，推导出其水平方向的公称切削分力表达式为

(25)

(26)

常用平底立铣刀为2～8齿，在β∈(0π]范围内，2齿立铣刀不存在多刃切削的工况，3齿立铣刀只存在单刃和两刃交替切削的工况，只有4～8齿立铣刀才存在完全多刃切削的工况。将推导得到的4～8齿平底立铣刀的水平方向公称切削力的函数系数AN和相位γN的值列于表1。

表1　铣削实验的切削参数4～8齿平底立铣刀的切削力仿真结果

1.3水平方向的公称切削力及其幅频谱仿真

用MATLAB软件编程的方法，模拟4～8齿平底立铣刀在单刃切削和多刃切削时的水平公称切削分力及其幅频谱。模拟参数为：铣刀齿数z为4～8，同时切削的刃数m为1～4，主轴转速1080r/min，采样频率4320Hz，tanφ=0.3[12-13]。用式(16)、式(18)模拟单刃切削力数据，采用1.2节中推导得到的多刃切削力表达式模拟多刃切削力数据。各工况下的浸入角、同时参与切削的刃数、水平方向切削分力及刀齿频率幅值见表1。

例如，对于8齿立铣刀，当浸入角β=π/4时为单刃切削，当β=π/2时为两刃切削，模拟得到这两种切削方式的水平方向切削分力及其幅频谱。图2所示为8齿立铣刀在单刃切削和两刃切削时的X向和Y向切削力及其幅频谱。

(a)X向切削力

(b)X向切削力幅值

(c)Y向切削力

(d)Y向切削力幅值图2　公称切削力及其幅频谱仿真 (z=8)

仿真得到4～8齿立铣刀在单刃切削和多刃切削时的水平方向切削力均值、刀齿频率的幅值，将其和对应的浸入角、同时参与切削的刃数列于表1。

由图2a、图2c可见，8齿立铣刀两刃切削时的水平合力显著大于单刃切削时的水平合力。可计算出8齿立铣刀在模拟条件下的刀齿频率为144Hz，由图2b、图2d可见，在刀齿频率处，X向的两刃切削力幅值小于单刃切削力幅值，而Y向的两刃切削力幅值大于单刃切削力幅值。

由表1可见，与单刃切削力相比，多刃切削力的特点有如下变化规律：

(1)在X方向，多刃切削力的均值可能比单刃切削力的均值更大，也可能更小。这是因为在旋转角小于π/2时和旋转角大于π/2时，X方向的切削力方向相反。若两个刀刃的旋转角分别为小于π/2和大于π/2，则其合力比单刃切削力小；若两个刀刃的旋转角都小于π/2，则其合力比单刃切削力大。表1显示出的增大和减小的分布规律与这一原因吻合。

(2)在Y方向，多刃切削力的均值显著比单刃切削力的均值大。这是因为在旋转角小于π/2时和旋转角大于π/2时，单个刀刃的Y向切削力的方向相同，所以，无论同时参与切削刀刃的旋转角如何分布，它们的Y向合力都比单刃切削时的Y向合力大。切削力均值是切削力的静态力，这一规律表明多刃切削时Y向静态分力显著增大。

(3)Y向切削力在多刃切削时与单刃切削时的比值大于切削刃数m，而式(24)显示水平切削分力的常数项与m成正比，两者的差异原因在于水平切削分力不是完整周期的简谐函数，其均值与常数项的相关性强，但不等于常数项。

(4)多刃切削时，Y向切削力均值大于X向切削力均值，在很多情况下远大于X向切削力均值。这是因为Y向多刃切削力常数项为mcosφ，X向多刃切削力常数项为msinφ，mcosφ≫msinφ，而常数项是均值的主要组成部分。例如，以2刃切削、tanφ=0.3计， mcosφ≈1.92，msinφ≈0.58。

(5)在多刃切削时，X向切削力的刀齿频率幅值比单刃切削时的小；Y向切削力的刀齿频率幅值有时显著小于单刃切削时的刀齿频率的幅值，而有时显著大于单刃切削时的刀齿频率的幅值。这是因为：① 对于4～8齿立铣刀，在1个刀齿周期内，单刃切削的刀刃旋转角最小为0，最大在π/4和π/2之间；多刃切削时，一个刃的旋转角与单刃切削相同，其他刃的旋转角在π/4和π之间。②单个刀刃的X向切削力在刀刃旋转角为0和π/2时约为0，在刀刃旋转角为π/4时约为最大值，在刀刃旋转角小于π/2时和大于π/2时方向相反。③单个刀刃的Y向切削力在刀刃旋转角为0和π时约为0，在刀刃旋转角为π/2时约为最大值，在刀刃旋转角小于π/2时和大于π/2时方向相同。因此，结合①、②可得，与单刃切削相比，多刃切削时X向切削力在一个刀齿周期内的动态变化程度要小；结合①、③可得，当较多的同时参与切削刀刃的最大旋转角小于π/2时，与单刃切削相比，多刃切削时Y向切削力在一个刀齿周期内的动态变化程度要大，而当较多的同时参与切削的刀刃的最大旋转角大于π/2时，多刃切削时Y向切削力在一个刀齿周期内的动态变化程度要小。表1显示的刀齿频率幅值增大和减小的分布规律与这一原因吻合。刀齿频率是动态力的主要频率成分，这一规律表明多刃切削时Y向动态力可能显著增大，也可能显著减小。

1.4变刃数连续切削的切削力变化规律探讨

只有浸入角取某些特定值时，在整个切削过程中才有单刃或多刃连续切削，而在其他取值时，都是断续的单刃切削，或变刃数的连续切削。例如，对于4齿立铣刀，浸入角β∈(π/2，π)时，为两刃-单刃的连续切削。在变刃数时，若浸入角接近多刃切削时的浸入角值，则因为切削工况接近多刃切削，切削力的变化规律将与多刃切削时相似；反之，则切削力的变化规律将与多刃切削时的差异较大。浸入角的边界取值尚需在后续研究中进一步明确。

对于4齿立铣刀，由式(18)、式(24)和表1可见，两刃切削的Y向切削力为常数2cosφ，等于单刃切削的Y向切削力最大值，因此在两刃-单刃切削时，Y向切削力的峰峰值将小于等于单刃切削时的峰峰值，即Y向切削力的变化较小，与单刃连续切削相比，变刃数切削将更平稳。

2试验

用φ10mm四齿硬质合金立铣刀在铣削加工中心上切削45钢材料。用北航SDC-C4F型测力系统(包括应变式测力仪、应变放大器和测力软件)同时测量X向、Y向和轴向三个切削分力，测力系统的灵敏度为66.66N/V。逆铣，空气冷却，切削深度0.5mm，每齿进给量0.12mm，主轴转速1080r/min，变切削宽度，采样频率4320Hz。切削宽度及对应的浸入角列于表2。可计算出实验的主轴旋转频率为18Hz，刀齿频率为72Hz。

表2　切削宽度及对应的浸入角

经225Hz低通滤波处理后，1号试验和4号试验的Y向切削分力数据如图3a和图3b所示，1～4号试验的Y向切削力均值及其刀齿频率幅值如图3c和图3d所示。

1号试验为单刃切削。单刃切削时，各刀齿的公称切削力波形相同，而图3a所示各齿的实测力大小不同。4号试验为双刃-单刃交替切削。4齿刀具在双刃切削时，公称力为常值，而图3b所示的切削力波形近似为台阶状。这些波形差异的原因在于实际切削力不仅包括公称力，还包括偏心力。不同刀齿的偏心力不相等，因此图3a的各刀齿实测Y向切削力不相同；各刀齿的理论偏心力的波形呈台阶状排列，因此图3b的切削力波形近似为台阶状。

由图3c和图3d可见，随着浸入角增大，即两刃切削的时间占比增大，Y向切削力的均值显著增大，而其刀齿频率的幅值显著减小，这和表1显示的切削力变化规律相符，也和1.4节所得的4齿立铣刀的变刃数切削力变化规律一致。

(a)1号试验的Y向切削力

(b)4号试验的Y向切削力

(c)Y向切削力的均值

(d)Y向切削力的刀齿频率幅值图3　实测Y向切削力及其幅频谱

3结论

(1)理论上，X、Y方向公称切削力的常数项与同时切削的刃数成正比。然而由于这些切削力不是完整周期的简谐信号，实际上多刃切削力均值与同时参与切削的刃数没有正比关系。

(2)多刃切削的Y向力均值大于X向力均值，表明多刃切削在切削宽度方向的静态力更大。

(3)与单刃切削相比，多刃切削的X向切削力的刀齿频率幅值总是减小的，而其Y向切削力的刀齿频率幅值有时减小、有时增大，这表明在水平方向，存在着多刃切削比单刃切削更平稳和更不平稳两种可能性。

(4)以表1为依据选择适当的浸入角，可提高4～8齿平底立铣刀的切削平稳性。常用的4齿、6齿、8齿平底立铣刀都存在动态公称切削力为0的浸入角，采用这些刀具和浸入角的切削最平稳。

(5)4齿立铣刀的2刃-单刃切削在切削宽度方向上比单刃切削更平稳。

参考文献：

[1]Bobrenkov O A, Khasawneh F A, Butcher E A, et al. Analysis of Milling Dynamics for Simultaneously Engaged Cutting Teeth[J]. Journal of Sound and Vibration, 2010, 329: 585-606.

[2]Kim G D, Chu C N. In-process Tool Fracture Monitoring in Face Milling Using Spindle Motor Current and Tool Fracture Index[J]. Int. J. Adv. Manuf. Technol., 2001, 18:383-389.

[3]Hwang J H, Oh Y T, Kwon W T, et al. In-process Estimation of Radial Immersion Ratio in Face Milling Using Cutting Force[J]. Int. J. Adv. Manuf. Technol., 2003, 22:313-320.

[4]李沪曾, 张国红, 魏衡. 多齿端铣切削振动的计算机仿真[J]. 同济大学学报, 2000, 28(1):55-59.

Li Huzeng, Zhang Guohong, Wei Heng. Computer Simulation of Cutting Vibrations in Face Milling with Multiblade Cutter[J]. Journal of Tongji University, 2000, 28(1):55-59.

[5]袁平. 采用多刃铣刀的航空铝合金高速加工过程的数值模拟与实验研究[D]. 杭州: 浙江大学. 2008.

[6]Salgado M A, López de Lacalle L N, Lamikiz A, et al. Evaluation of the Stiffness Chain on the Deflection of End-mills under Cutting Forces[J]. Int. J. Mach. Tools Manuf., 2005, 45: 727-739.

[7]Krüger M, Denkena B. Model-based Identification of Tool Runout in End Milling and Estimation of Surface Roughness from Measured Cutting Forces[J]. Int. J. Adv. Manuf. Technol., 2013, 65:1067-1080.

[8]Sun Yujing, Sun Jie, Li Jianfeng, et al. Modeling of Cutting Force under the Tool Flank Wear Effect in End Milling Ti6Al4V with Solid Carbide Tool[J]. Int. J. Adv. Manuf. Technol., 2013, 69:2545-2553.

[9]李炳林, 胡于进, 王学林,等. 基于斜角切削理论的立铣切削力预测研究[J]. 中国机械工程, 2011, 22(19):2283-2288.

Li Binglin, Hu Yujin, Wang Xuelin, et al. Cutting Force Prediction Based on Oblique Cutting Theory in End Milling[J]. China Mechanical Engineering, 2011, 22(19):2283-2288.

[10]Tlusty J, Macneil P. Dynamics of Cutting Forces in End Milling[J]. Annals of the CIRP, 1975, 24(1):21-25.

[11]刘璨, 吴敬权, 李广慧,等. 基于单刃铣削力峰值的铣刀偏心辨识[J]. 机械工程学报, 2013, 49(1): 185-190.

Liu Can, Wu Jingquan, Li Guanghui, et al. Identification of Mills Eccentricity Based on Peak Force of Single Edge[J]. Journal of Mechanical Engineering, 2013, 49(1):185-190.

[12]Janez G, Martin K, Klaus W. Mechanistic Identification of Specific Force Coefficients for a General End Mill[J]. Int. J. Mach. Tools. Manuf., 2004, 44:401-414.

[13]Engin S, Altintas Y. Mechanics and Dynamics of General Milling Cutters—Part I: Helical End Mills[J]. Int. J. Mach. Tools. Manuf., 2001, 42:2195-2212.

(编辑苏卫国)

Study on Variation Regulation of Cutting Forces in Multi-edge Cutting with Flat End Mills

Liu CanWu JingquanLiu HuanlaoTan Guangyu

Guangdong Ocean University, Zhanjiang, Guangdong, 524088

Abstract:For revealing the regularity of cutting force varying in multi-edge milling with flat end mills, the mathematical expressions of nominal cutting forces in horizontal directions were deduced, and these cutting forces were found to be harmonic functions of rotational angle, their constants were in proportion to the numbers of simultaneously cutting edges. With normalizing the coefficients of cutting force expressions, and applying simulation method, the dimensionless means and amplitudes at tooth frequency of nominal cutting forces for flat end mills with common flute were obtained. The simulation results show that: in multi-edge cutting, the means of nominal cutting force in radial depth direction prominently increases, while its amplitudes at tooth frequency either increase or decrease. Experiments of cutting and force measuring for 4-flute flat end mill were done, the results agree with those of mathematically deduction and simulation. Research results imply that, comparing with single-flute continuous cutting, the static cutting force in radial depth direction of multi-edge cutting will prominently increase; in horizontal directions, multi-edge cutting may be more or less stable; the multi-edge cutting with even-flute mills may be especially stable. Research results can be used in milling for selecting immersion angle optimally.

Key words:end mill; multi-edge cutting; cutting force; stability; immersion angle

收稿日期：2015-10-08

基金项目：国家自然科学基金资助项目(51375099,51375100)

中图分类号：TH161

DOI：10.3969/j.issn.1004-132X.2016.10.012

作者简介：刘璨，男，1971年生。广东海洋大学工程学院副教授、博士。研究方向为机械加工过程的监测控制。吴敬权，男，1980年生。广东海洋大学工程学院实验员。刘焕牢，男，1967年生。广东海洋大学工程学院教授、博士。谭光宇(通信作者)，男，1957年生。广东海洋大学工程学院教授、博士。