飘浮基两杆柔性空间机械臂的振动分析与振动抑制

于潇雁，陈　力

(1．福州大学机械工程及自动化学院，福州 350116；2．福建省高端装备制造协同创新中心，福州 350116)



飘浮基两杆柔性空间机械臂的振动分析与振动抑制

于潇雁1,2，陈力1

(1．福州大学机械工程及自动化学院，福州 350116；2．福建省高端装备制造协同创新中心，福州 350116)

摘要:对载体位置无控、姿态受控的飘浮基两杆柔性空间机械臂操作过程中的振动进行了分析，并提出了对振动进行有效抑制的方法。首先利用拉格朗日方程并结合系统总质心定义，得到系统的动力学方程。然后对该系统操作过程中的振动进行了分析。接着利用奇异摄动法，将两杆柔性空间机械臂系统分解为一个关于载体姿态、杆件关节轨迹跟踪的慢变子系统和一个描述柔性臂变形的快变子系统。以此为基础，提出了一个由慢变控制项和一个快变控制项组成的复合控制器，使得机械臂在操作过程中跟踪上载体姿态和关节期望轨迹的同时柔性臂的振动得到了有效的抑制。该控制方案的显著优点为不需要测量反馈载体的位置、移动速度、移动加速度。

关键词:飘浮基柔性空间机械臂；载体姿态受控；奇异摄动法；振动分析；振动抑制

1引言

在未来的空间操作作业中，空间机器人将扮演着重要的角色，其应用将减少宇航员舱外活动的危险和载人航天的费用，因此各国研究人员对空间机器人进行了广泛的研究[1-5]。由于工作地点是太空这一特殊环境，空间机器人系统的机械臂与载体之间存在着强烈的动力学耦合问题，其动力学和控制问题远比地面固定基机器人来得复杂。为了节省发射费用，空间机械臂系统需越来越轻，从而导致机械臂的柔性越来越大。由于刚性运动和柔性振动的相互作用，每一个关节的控制力矩不但要保证跟踪上关节期望运动轨迹，同时要控制相应的柔性臂的振动，使得控制漂浮基柔性空间机器人要比相应的刚性空间机器人复杂得多。

目前对空间机械臂的研究主要集中在刚性空间机械臂和刚柔混合的空间机械臂。Walker[6]和马保离等[7]讨论了载体位置无控、姿态受控空间机械臂的自适应控制问题。Gu等[8]对载体位置和姿态均不受控制的情形，提出了自适应控制的标准形式增广法。陈力[9]则给出了带滑移铰空间机械臂惯性空间的复合自适应控制方案。洪昭斌等[10]利用奇异摄动理论实现了刚柔混合的飘浮基空间机械臂的模糊控制。

从节省控制燃料、增加空间机器人系统的有效使用寿命、减少发射费用的角度考虑，使用载体位置、姿态均不受控制的空间机器人系统将非常必要。但为了保证通信设备、视觉设备和太阳能帆板正常工作，空间机器人系统的载体必须保持一定的姿态，因此空间机器人系统也常设计为载体位置不控、姿态受控的形式。本文对载体位置不控、姿态受控的飘浮基柔性空间机械臂操作过程中的振动进行了分析，并提出了对振动进行抑制的方法。首先利用拉格朗日方程并结合系统总质心定义，得到系统的动力学方程；然后对该系统操作过程中的振动进行了分析；接着利用奇异摄动法，将柔性空间机械臂系统分解为一个关于载体姿态和杆件关节轨迹跟踪的慢变子系统和一个描述柔性臂振动快变子系统。以此为基础，提出了一个由慢变控制项和快变控制项组成的复合控制器。其中，慢变控制项实现载体姿态、杆件关节轨迹跟踪控制。柔性臂快变控制项使柔性臂振动得到有效的抑制。

2机械臂动力学建模

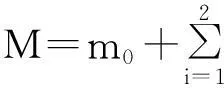
图1　飘浮基柔性空间机械臂系统Fig.1　A planar flexible free-floating space manipulator

建立平动的惯性坐标系(O-xy)，设各分体在(x,y)平面作平面运动，θ0、θ1和θ2分别为系统载体姿态及机械臂关节铰的相对转角，载体和柔性臂B1、B2的质心OCi(i=0,1,2)相对于惯性坐标系原点O的矢径为ri。

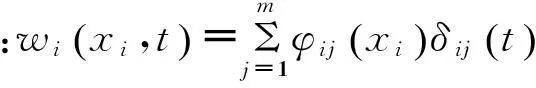
由系统位置几何关系及利用系统总质心定义，载体质心矢径r0可表示为式(1)：

(1)

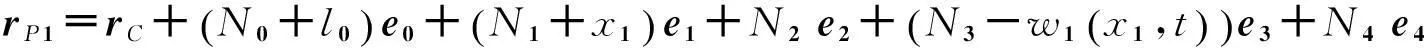
(2)

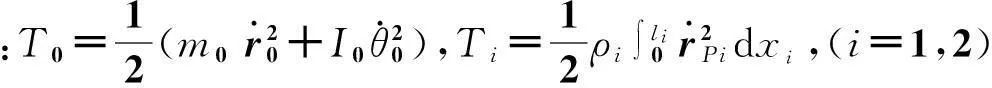
忽略太空中的微重力，整个系统的总势能V为式(3)：

(3)

可以得到系统的Lagrange函数 L=T-V。根据第二类Lagrange方程，可以推导得到这个载体位置不控、姿态有控的柔性空间机械臂系统的动力学方程如式(4)：

(4)

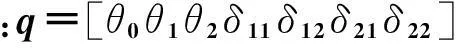
3机械臂操作过程中的振动分析

(5)

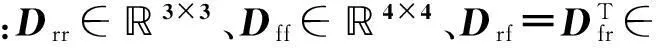
由于Dff可逆，由(5)式第二式可得式(6)：

(6)

将(6)式代入(5)式第一式得到式(7)：

(7)

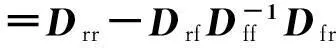
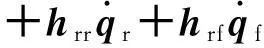
设计基于模型的控制律如式(8)：

(8)

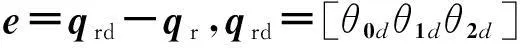
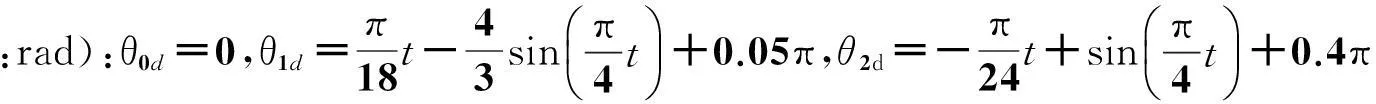
仿真运动初始值均取为：δ11(0)=δ12(0)=0 m，δ21(0)=δ22(0)=0 m，θ0(0)=0.1 rad，θ1(0)=0.05π-0.1 rad，θ2(0)=0.4π+0.2 rad，整个追踪过程所用的时间t=10 s。控制器的参数Kd=Kp=diag([40,40,40])。

仿真结果如图2—图7所示。图2为机械臂载体姿态角、关节铰的轨迹跟踪图；图3、图4分别为柔性杆1一阶、二阶振动模态；图5、图6分别为柔性杆2一阶、二阶振动模态；图7为系统的输入力矩。

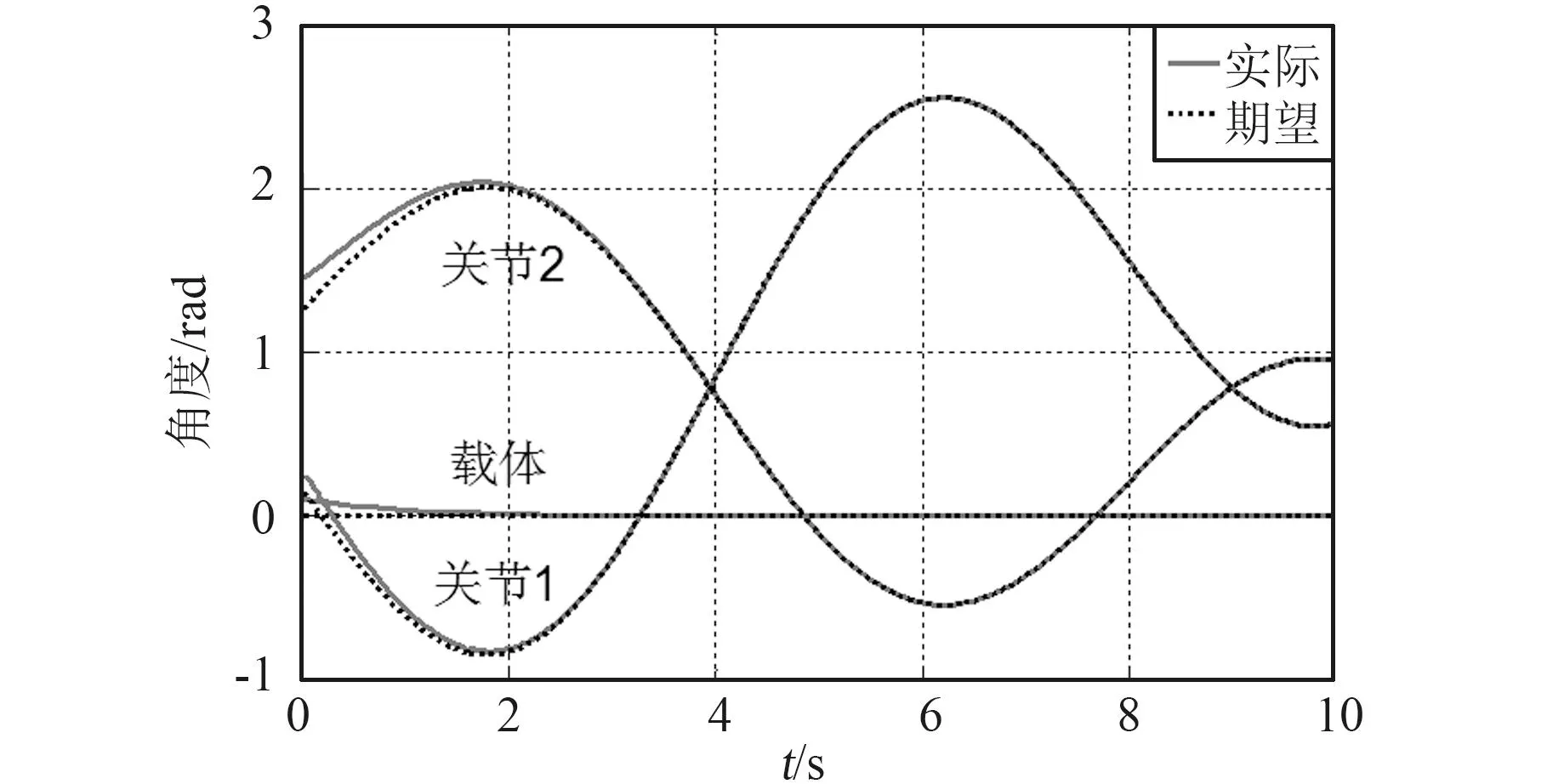
图2　系统载体姿态、关节的轨迹跟踪图Fig.2　Comparison between the actual angular trajectory and the desired one of the base attitude and the joints

图3　杆1一阶振动模态Fig.3　The first vibration mode of link 1

图4　杆1二阶振动模态Fig.4　The second vibration mode of link 1

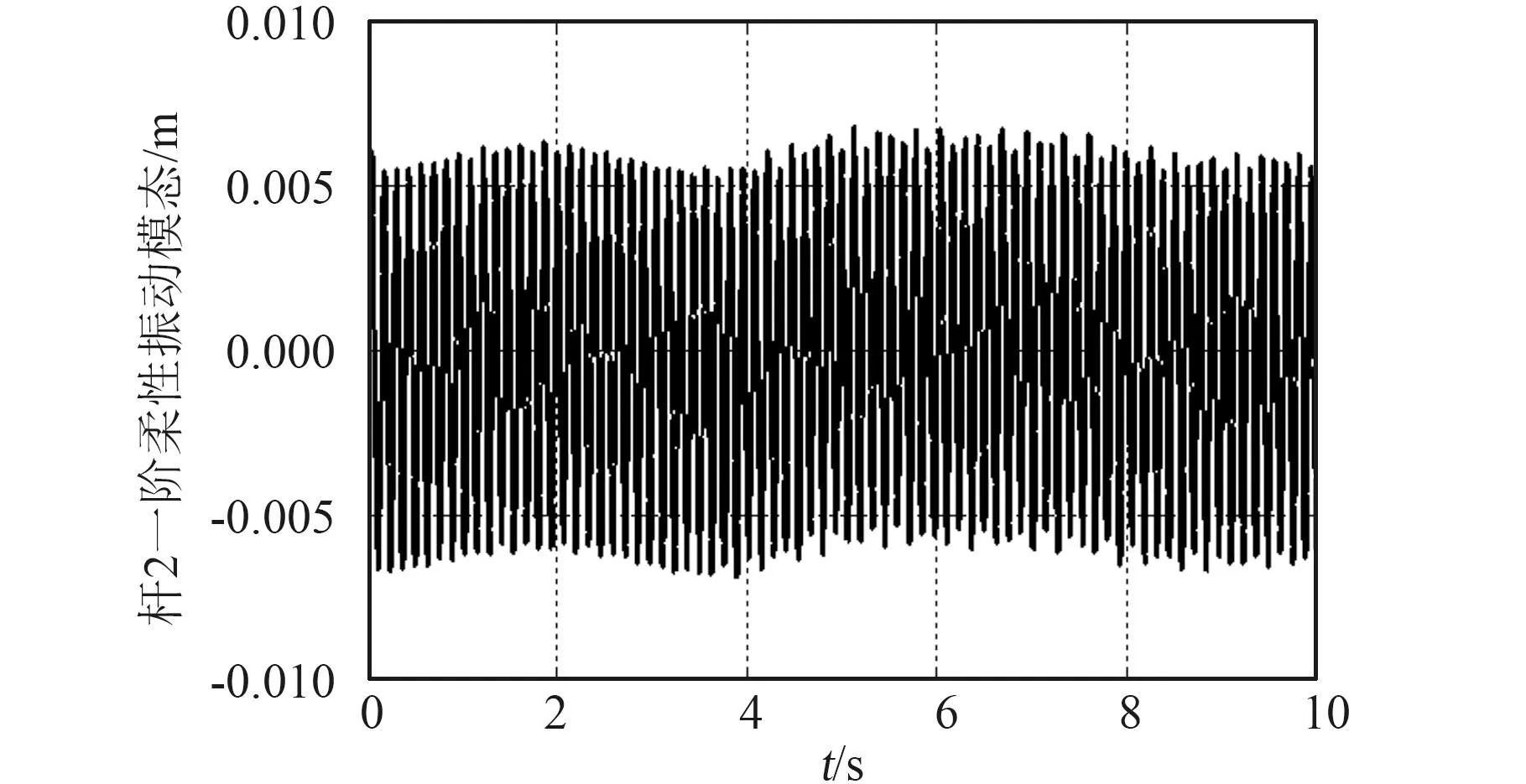
图5　杆2一阶振动模态Fig.5　The first vibration mode of link 2

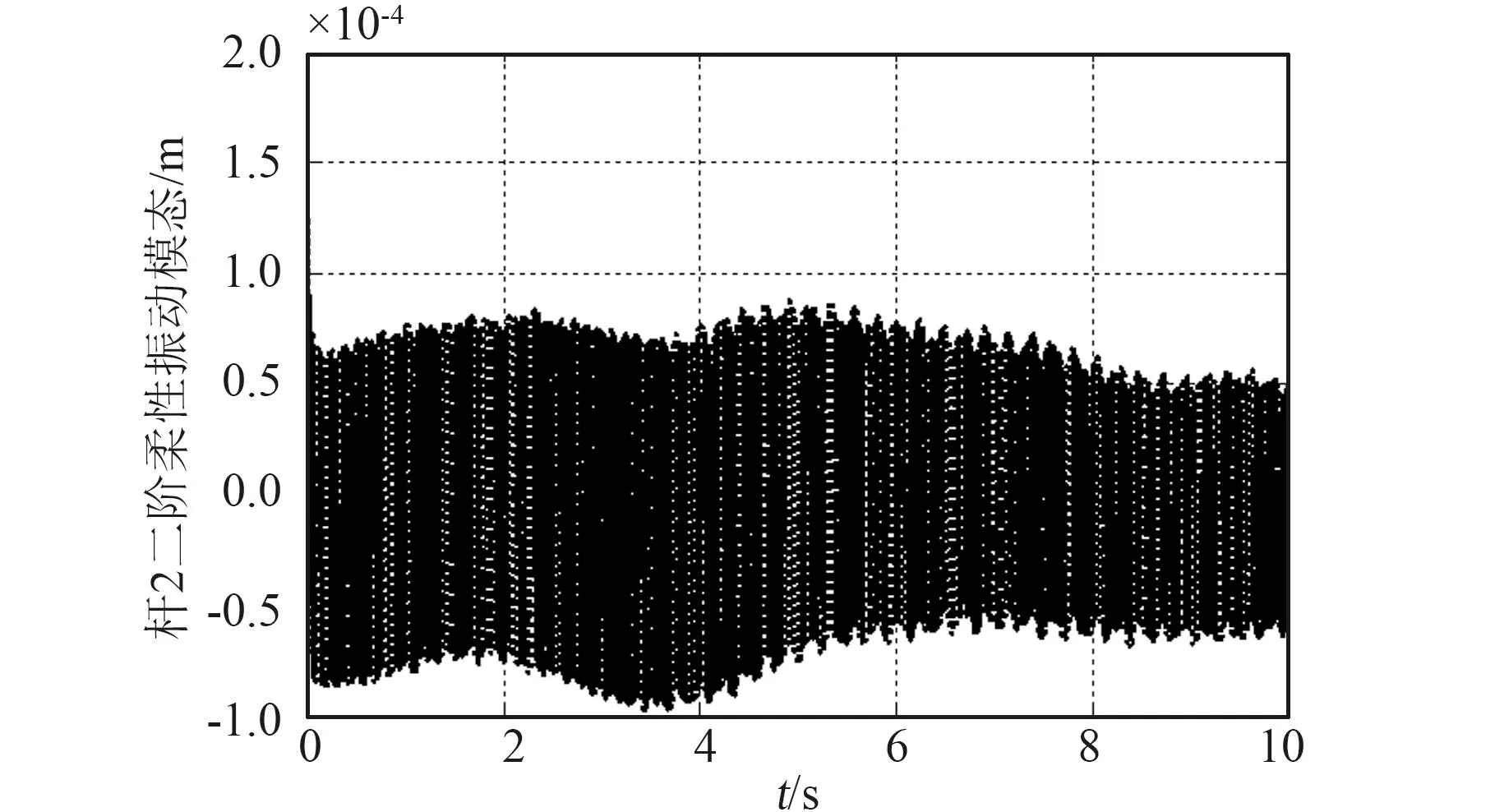
图6　杆2二阶振动模态Fig.6　The second vibration mode of link 2

图7　输入力矩Fig.7　The input torque

从仿真结果可以看出，在有着较大初始误差的情况下，PID控制能够使载体姿态、机械臂关节轨迹快速而稳定地追踪上期望运动轨迹。但是系统始终存在比较大的振动。为了消除柔性臂的振动，提高柔性空间机械臂的操作性能，有必要对柔性臂的振动进行抑制。

4机械臂操作过程中的振动抑制

由于与载体姿态和关节铰的运动相比，柔性杆的振动为高频振动，所以载体姿态、关节轨迹跟踪控制和柔性臂的振动抑制的时间尺度是可以通过奇异摄动理论[12]分开考虑的。

4.1动力学模型的奇异摄动分解

由于系统惯性矩阵D是对称、正定的，因此其逆矩阵可定义为式(9)所示N：

(9)

式中：

则式(5)可以写为式(10)：

(10)

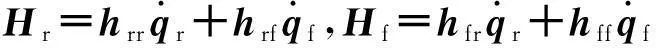
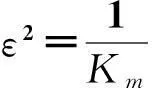
(11)

为了得到漂浮基柔性空间机械臂的慢变子系统，设(11)式中的ε等于零，那么可得式(12)：

(12)

由(12)式第二式可得式(13)：

(13)

(14)

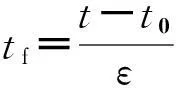
令ε=0并利用(12)式中的第二式，可得快变子系统近似表达式如式(15)：

(15)

(16)

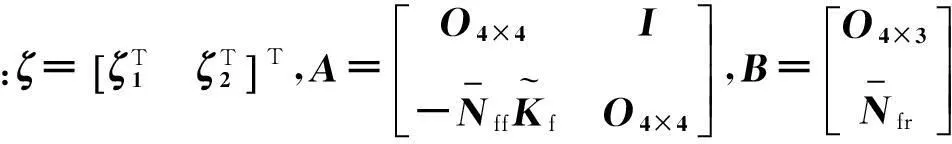
4.2振动抑制的复合控制器设计

对于式(17)所示的慢变子系统，设计基于模型的控制律：

(17)

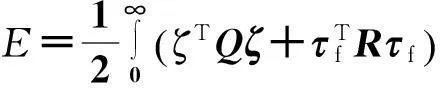
(18)

其中P为Ricatti方程PA+ATP-PBR-1BTP+Q=O的解。

仿真结果如图8～13所示。图8为机械臂载体姿态角、关节铰的跟踪位置误差图，图9、图10分别为柔性杆1一阶、二阶振动模态，图11、图12分别为柔性杆2一阶、二阶振动模态，图13为系统的输入力矩。

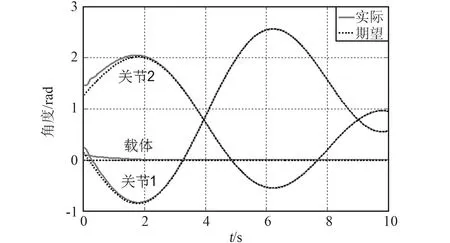
图8　系统载体姿态、关节的轨迹跟踪图Fig.8　Comparison between the actual angular trajectory and the desired one of the base attitude and the joints

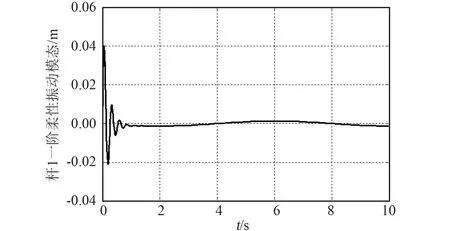
图9　杆1一阶振动模态Fig.9　The first vibration mode of link 1

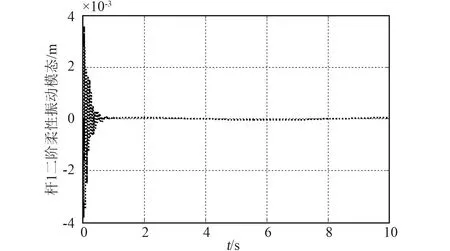
图10　杆1二阶振动模态Fig.10　The second vibration mode of link 1

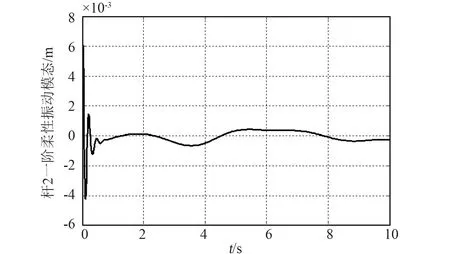
图11　杆2一阶振动模态Fig.11　The first vibration mode of link 2

图12　杆2二阶振动模态Fig.12　The second vibration mode of link 2

图13　输入力矩Fig.13　The input torque

从仿真结果可以看出，在有着较大初始误差的情况下，所设计的基于奇异摄动理论的复合控制器能够快速跟踪上载体姿态、关节铰期望轨迹，同时也使柔性臂的振动得到了有效的抑制。

5结论

1)本文利用拉格朗日方程并结合系统总质心定义，建立了一个具有两个柔性臂的飘浮基空间机械臂系统动力学模型。

2)在有较大初始误差的情况下，对飘浮基柔性空间机械臂进行PID控制，使载体姿态、机械臂杆件关节轨迹快速而稳定地追踪上机械臂期望的运动轨迹。但是系统始终存在比较大的周期性振动。

3)利用奇异摄动法，将这个柔性空间机械臂系统分解为一个慢变子系统和一个柔性臂快变子系统。对慢变子系统设计PID子控制器跟踪载体姿态和关节期望轨迹，对柔性臂快变子系统设计一个最优线性子控制器来抑制柔性臂的振动。然后将慢变子控制器与柔性臂快变子控制器组合成一个复合控制器。在有着较大初始误差的情况下，这个基于奇异摄动理论设计出的复合控制器能够快速跟踪上载体姿态、机械臂关节期望轨迹，同时也使柔性臂的振动得到了有效的抑制。这种方法可以推广到具有任意个柔性杆的飘浮基空间机械臂系统中。

参考文献(References)

[1]BoumansR.,HeemskerkC.TheEuropeanroboticarmfortheInternationalSpaceStation[J].RoboticsandAutonomousSystems, 1998, 23(1): 17-27.

[2]GarneauM.Spaceintheserviceofsociety:acanadiancasestudy[C]//Proceedingsof2ndInternationalConferenceonRecentAdvancesinSpaceTechnologies,Istanbul,Turkey, 2005. 1-6.

[3]NohmiM.Developmentofspacetetheredautonomousroboticsatellite[C]//Proceedingsof3rdInternationalConferenceonRecentAdvancesinSpaceTechnologies,Istanbul,Turkey, 2007. 462-467.

[4]HolcombLB,Montemerlo,MD.NASAautomationandroboticstechnologyprogram[J].IEEEAerospaceandElectronicSystemsMagazine, 2009, 2(4): 19-26.

[5]YoshidaK.Achievementsinspacerobotics[J].IEEERoboticsandAutomationMagazine, 2009, 16(4): 20-28.

[6]MichaelW.Adaptivecontrolofspace-basedrobotmanipulators[J].IEEETransactionsonRoboticsandAutomation, 1992, 7(6): 828-835.

[7]马保离, 霍伟. 空间机器人系统的自适应控制[J]. 控制理论与应用, 1996, 13(2): 191-197.

MaBL,HuoW.Adaptivecontrolofspacerobotsystem[J].ControlTheoryandApplications, 1996, 13(2): 191-197.(inChinese)

[8]GuYL,XuYS.Anormalformaugmentationapproachtoadaptivecontrolofspacerobotsystems[J].JournaloftheDynamicsandControl, 1995, 5(3): 275-294.

[9]陈力. 带滑移铰空间机械臂惯性空间轨迹的复合自适应跟踪控制 [J]. 空间科学学报, 2003, 23(1): 60-67.

ChenL.Compositeadaptivecontrolofspacemanipulatorsystemwithprismaticjoint[J].ChineseJournalofSpaceScience, 2003, 23(1): 60-67.(inChinese)

[10]洪昭斌, 陈力. 漂浮基柔性空间机械臂基于奇异摄动法的模糊控制和柔性振动主动控制.机械工程学报[J]. 2010, 46(7): 35-41.

HongZB,ChenL.Activevibrationcontrolandfuzzycontroloffree-floatingspaceflexiblemanipulatorbasedonsingularperturbationtheory[J].JournalofMechanicalEngineering, 2010, 46(7): 35-41.(inChinese)

[11]LucaAD,SicilianoB.Closed-formdynamicmodelofplanarmultilinklightweightrobots[J].Systems,ManandCybernetics,IEEETransactionson, 1991, 21(4): 826-839.

[12]KokotovicP,KhalilHK,O′reillyJ.SingularPerturbationMethodsinControl:AnalysisandDesign[M].Cambridge,MassachusettsUSA:AcademicPress, 1986: 56-71.

Vibration Analysis and Suppression of Free-floating Space Manipulator with Two Flexible Links

YU Xiaoyan1,2, CHEN Li1

(1.School of Mechanical Engineering and Automation, Fuzhou University, Fujian 350116, China;2. Fujian Provincial Collaborative Innovation Center for High-end Equipment Manufacturing,Fuzhou University, Fuzhou 350116, China)

Abstract:A free-floating flexible space manipulator with two flexible links was presented in this paper. The dynamical Lagrange equation was established and the flexible links’ vibration was analyzed. Then a singularly perturbed model was formulated and applied to the design of a reduced-order controller. This controller consists of a rigid control component and a fast control component. The rigid subsystem controller will track the desired trajectories of the base attitude and the joints. The flexible-link fast subsystem controller will damp out the vibration of the flexible links. Numerical simulations showed that the links’ vibration was stabilized effectively with good tracking performance.

Key words:free-floating flexible space manipulator; controlled base attitude; singular perturbation approach; vibration analysis; vibration suppression

收稿日期：2014-09-12；修回日期：2016-04-27

基金项目：国家自然科学基金(11372073，11072061)；福建省自然科学基金(2016J01228)

作者简介：于潇雁(1974-)，女，博士，副教授，研究方向为机构学、空间机器人系统动力学与非线性控制。E-mail：cool09@163.com

中图分类号：TP241

文献标识码：A

文章编号：1674-5825(2016)03-0354-07