量子计算机概述
2016-06-03杨洪应
杨洪应
摘 要 众所周知,计算机的发明为许多进行大量计数字运算的问题提供了一条捷径,其能力是一般的人工无法比拟的。但是有的问题是经典计算机无法解决的,运用量子计算却能很快的解决。本文将对量子计算机做一个简单介绍。
关键词 量子信息 量子比特 量子计算机 Shor算法
中图分类号:O561 文献标识码:A
0引言
半导体工业在过去的几十年发展表明:计算机的中央处理器在每1-2年就会增长一倍,芯片上的集成的晶体管数目更是呈指数形式增长。在不远的将来每个芯片上的晶体管将会超过十亿个,这样的增长速度使得半导体的加工变得越来越困难。另一方面,随着纳米技术的发展,今后计算机的储存尺度单位将是原子级别的。当人们把这些器件加工到原子尺度程度的时候,就应该用量子理论来描述这些性质。量子理论作为描述微观世界的理论,它具有与经典理论有许多的不同之处,甚至和我们日常经验发生矛盾。
在1994年Peter Shor首次提出一种具体的量子大数因子分解加密算法,这个对RSA等公钥密码系统的安全性来说是一个挑战。随后在1996年,Grover发现了Grover迭代算法,它能求解某些解典计算机不能解决的问题,如经典的NPC问题。除此外,利用量子不可克隆实现保密通信,可以防止通信过程中被监听。这些性质使得量子通信具有广泛地应用前景而成为一个较热的课题。量子信息和量子计算已被我国列入“十三五”重大研究课题。
1量子比特
在经典的计算机里,基本的构造单元是比特。不论是用电子管来实现的一个比特还是用晶体管来实现的比特,其基本原理都要遵从牛顿力学定律。在一个经典的计算机里,其储存量是用比特的多少来衡量的。它的运算速度可有单位时间内比特的转换数目来决定。
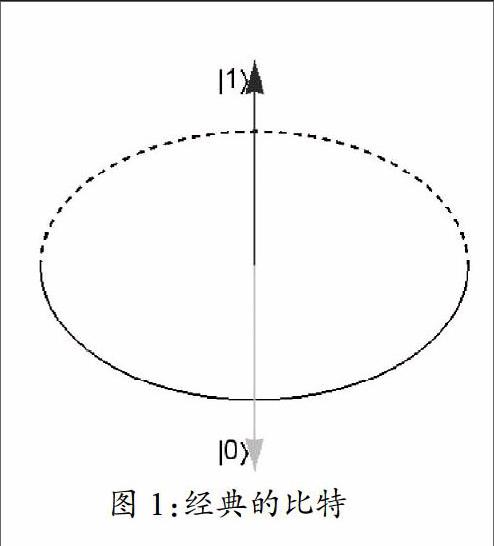
在图1中可以看到,经典的比特实质是就是两个点10>和11>,所以在储存的时候也只能是10>和11>。因此我们想要提高其运行速度就受到了原理上的限制。首先是我们在追求速度时,就需要不断地提高微电子元件的集成度,小型化的电子器件必然会受到量子极限尺寸的限制。其次就是由于经典计算机的操作是不可逆的,由热力学原理知道,计算芯片必然发热,这是提高经典计算机的计算能力主要障碍。最后就是经典计算机不具备内在的并行运算。通过连接更多的计算资源来解决并行运算是比较复杂且难以实现的。
2量子比特
量子比特是计算信息科学里一个重要的概念,是量子计算机的基本单元,因此在这里我们对它做一个详细的介绍。
量子比特其可以对应量子力学里一个粒子态的叠加,对于一个自旋为1/2的粒子,其本征态为两种定态 ,单粒子的叠加态可表示为
| >= |1>+ |0> (1.1)
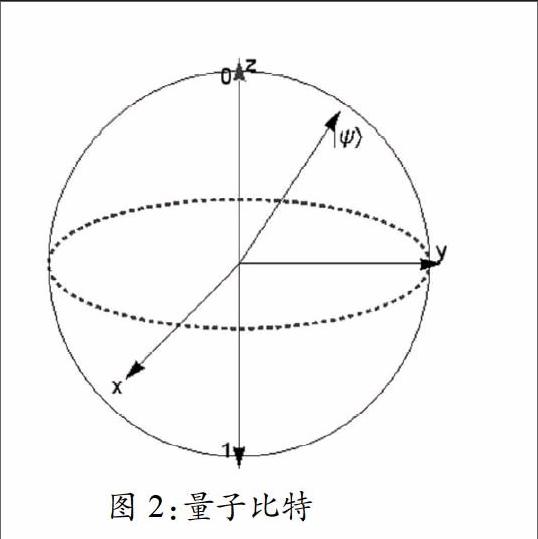
这里的 , 为任意复数,其分别对应两个定态在叠加态中所占的比例,如果 =0或者是 =0 时,叠加态就转化为定态,两个系数的模方 分别代表粒子状态在每一个定态中的几率。Bloch球面中则表示在量子力学里一个一把态的叠加。我们可以看到,经典的两个比特只是Bloch球面中一种特殊的情况,其被Bloch球面所包围。而量子态在三维的坐标中表示出来就是Bloch球面上的一个点。所以一个量子比特有无穷个态,每个态对应Bloch上的一个点,对量子比特进行操纵,就是把Bloch球面上的一个点移到另外的一个点,这个操纵是一个幺正变换。
3量子计算机
从(1.1)式我们可以看到,经典计算机是只是量子计算机的特例,量子计算机是经典计算机的推广,这一推广使得其计算能力成指数倍的增长。对于由量子力学原理所支配的量子计算机来说,原则上制约着经典计算机计算能力的原理都不存在,首先因为构成量子计算机的一些芯片实质上就是量子器件。其次是量子计算是由一系列幺正演化来完成的,所以这是一个可逆的过程,不存在耗热问题。最后就是量子计算是建立在量子叠加态基础上的,所以具有并行性运算能力。因而某些在经典的计算机里需要进行指数倍运算,在量子计算机里却只需进行多项式分解运算。
其实,在早期(1982年)就有人预想到了量子元件的计算能力比经典的元件强很多,不过在这个时期并没有受到人们的关注。直到20世纪初Shor首次提出Shor算法后使得量子计算机有了现实意义,即能对现行信息安全所依仗的大数因子分解难题进行有效的破解。从此以后就有越来越多的科研工作者开始关注量子计算机,关心和探讨适合量子元件运算规律的算法。
要实现量子计算过程,大致有一下三个步骤:
首先是初态的制备,在经典的计算机中,进行一个有用的计算最重要的要求是制备期望的输入。同样在量子计算机里,我们将芯片中的各个比特制备在某个特定的量子态上,这个过程中要求比特保持良好的量子相干性,以便保证量子叠加态能够一直成立。
其次是去实施完成所预想的各种可逆幺正变换,这些幺正变换就是我们通常所说的各种操作。在量子计算机里,人们相信量子计算机和经典计算机一样,都是由一系列的基本的逻辑运算组成。目前已经证明任何的量子计算都可以通过一个基本量子逻辑门集的组合来完成。
最后就是信息的读取,对量子器件进行测量来读出计算结果。需要注意的是,量子力学所掌握的是关于微观系统的规律是一种统计规律,它只能告诉我们在某个时刻一个微观系统的各个物理量取不同值的概率。在大多数时候,我们得到的末态有可能也是一个量子叠加态,所以我们测量的结果一般都是概率性的。量子计算通常要重复多次才能得到比较明确的结果。
4量子算法
在Shor算法为提出以后,人们意识到这将对当今广泛应用着的公匙密码体系的安全性构成严重的威胁,因为它能实现大数因子分解。
通常来说,RSA公匙密码体系中,密码的生成方式是这样的:第一步是去寻找两个大的质数m,n,计算Q=mn的值以及欧拉函数 (Q)=(m 1) (n 1)。第二步是在区间1≤e≤ (Q)随机选择一个和 (Q)互质的整数,计算模 (Q)下的逆元d=e-1mod (Q);最后一步是定义公匙私匙(M,e)是d。
由此可知,RAS公匙密码的安全性完全取决于大整数n的质因数分解的困难性,目前经典计算机是不能破解的。而在物理上,Shor量子算法是有效的,Shor算法是对大数因子分解的一种有效的算法:其复杂程度随着问题的规模只是多项式的增加。
5结论
在本文我们介绍了经典的比特和量子比特。经典的比特只是Bloch球上的两个点,而量子比特则是Bloch球上的所有点。可以看出,经典比特只是量子比特的一种特例。同时我们也讨论了经典的计算机和量计算机,量子计算机所执行的是一个可逆幺正演化且具备并行运算的能力,使得量子计算机能解决经典计算机所不能解决的问题,尤其是对大数因子的分解。量子计算机是目前量子信息科学中最重要的研究领域之一,这将是目前以及未来一段时间内科学家门所要研究的重点。
参考文献
[1] Shor P W.Scheme for reducing decoherence in quantum computer memory,Phys.Rev.A.1995,52(4):2493-2496.
[2] Geover L K,Quantum computers can search rapidly by using almost any transformation.Phys.Rev.Lett.1998,80(19):4329-4332.
[3] M.A.Nielsen and I.L.Chuang,Quantum Computation and Quantum Information (Cambridge University Press,U.K,2000)
[4] 曾谨言.量子力学(卷二)[M].科学出版社,2007
[5] 梁九卿.量子物理新进展[M],科学出版社,2011.
