类谐波积谱基音周期检测算法

梅铁民，付天娇,朱向荣

(1.沈阳理工大学 信息科学与工程学院，沈阳 110159；2.淄博民通热力有限公司，山东 淄博 255400)



类谐波积谱基音周期检测算法

梅铁民1，付天娇1,朱向荣2

(1.沈阳理工大学 信息科学与工程学院，沈阳 110159；2.淄博民通热力有限公司，山东 淄博 255400)

摘要：基音周期检测是语音信号处理的一项重要内容。在低信噪比情况下，常用的自相关函数法容易出现半周期和倍周期估计错误。为解决这一问题，在谐波积谱法的启发下提出了基于自相关函数的类谐波积谱法。该方法不仅可以有效地克服谐波积谱法由于信号中某次谐波分量为零时所造成的困难，而且可以有效地提高低信噪比下基音周期检测的可靠性。

关键词：基音周期；自相关函数；类谐波积谱

随着信息科学技术的不断发展，语音信号处理的重要性日益突出。语音信号处理主要研究包括语音编码、语音识别、说话人识别、语音合成等方向。在这些研究中，均需要对语音信号进行特征参数分析。基音周期估计是语音信号的重要特征参数之一[1]，对它估计的准确性直接影响到语音编码、语音识别、说话人识别、语音合成的质量[2]。

基音周期检测技术主要有时域的自相关法[3]、频域的倒谱法、谐波积谱法、时频结合的小波变换分析方法以及在其基础上的衍生算法[4]。常用的自相关基音周期估计方法计算简单，并且高信噪比下比较可靠，但当信号的信噪比较低时，该方法会出现半周期或多倍周期的估计错误。谐波积谱法是通过估计语音信号的基频来估计基音周期的一种频域算法，它可以有效地克服半周期或多倍周期错误，但是当语音信号某一谐波分量为零时，该方法将遇到困难。为了克服以上两种方法存在的不足，本文提出基于自相关函数的类谐波积谱基音周期估计方法，该方法可以有效地克服以上这些问题。

1谐波积谱法与类谐波积谱法

1.1谐波积谱

在时域中，基音周期检测的精度受到采样周期的限制，而在频域中，利用短时频谱进行基音周期检测时则不受这种制约，精度可以高于一个采样周期。频域基音检测方法中，一种常用的有效方法是谐波积谱法。

谐波积谱法(Harmonic Product Spectrum，HPS)是根据语音信号的短时谱Xn(ejw)检测基音频率f0。这种方法通过将多个谐波的能量累积起来，寻找谐波积谱的最大值来确定基音频率。信号x(n)的谐波积谱定义为

(1)

对上式两边取对数，可得x(n)的对数谐波积谱为

(2)

式中Xn(ejiw)是短时谱Xn(ejw)在频域压缩i倍的结果，它的i次谐波的峰值位置总是与Xn(ejw)的基波频率对齐。所以，不管原来的频谱中基波成分是否具有最高的峰，谐波积谱Pn(ejw)都会在基频处出现最高的峰，这可以有效地降低基音频率估值落到倍频或分频上的可能性。由于噪声频谱中没有相干的结构，所以这种技术特别适用于对抗加性噪声，能有效地检测出语音信号基音频率f0[5]。但它的不足之处是当某一谐波分量为零时将使谐波积谱中基频处的值为零，给基频估计造成困难。

1.2类谐波积谱法

受谐波积谱法的启发，可以把该方法做如下推广。对任何具有周期性信号频谱特征的函数都可以定义一个类似于谐波积谱的函数，以突出该函数中以坐标原点为始点，以固定周期出现的分量，从而可以准确地估计该周期。周期性信号频谱的特征就是其谐波分量以零频(即频率坐标的原点)为始点，以基频为周期重复出现，因此谐波积谱可以显著提高基频处的峰值。

但是，谐波积谱法也存在一定的缺陷，即当信号中某次谐波分量极微弱或不存在时，谐波积谱的基频位置将不再是最大峰值位置，这将给基频的估计带来困难。因此，类谐波积谱算法是将谐波积谱中的累积运算改为累加运算，这样就可以避免如上所述的困难。

令p(t)表示具有周期性信号频谱特征的函数，变量t可以是频率、时间或距离，或任何其它物理量。信号p(t)的类谐波积谱可定义为

(3)

类谐波积谱函数Q(t)在信号p(t)的第一个周期处的值将是函数p(t)在前m个周期处的值之和，即将周期性信号p(t)所有峰值叠加到Q(t)的第一个峰值处，使Q(t)在第一周期处形成最大峰值。如果信号p(t)的前m个周期处的峰值中，由于噪声影响，某个值可能很小，甚至接近零，对Q(t)在第一周期处的峰值影响并不大。因此，这样定义的类谐波积谱函数可以有效地克服谐波积谱函数的不足。

2基于自相关函数的类谐波积谱算法

自相关函数法是语音信号基音周期估计中的一种常用方法。语音信号中的浊音段具有准周期性，因而其自相关函数也具有准周期性。自相关函数第一峰值处所对应的时间即为语音的基音周期，因此可以通过检测自相关函数第一峰值来估计基音周期。在信噪比较低的情况下，自相关函数第一峰值的位置不易准确估计，给基音周期估计带来困难。由于准周期语音信号的自相关函数的峰值分布规律与其频谱中各次谐波分量的分布规律一致，因此可以定义基于自相关函数的类谐波积谱函数来估计基音周期。

自相关函数主要用于衡量信号自身时间波形的相似性，由于清音和浊音的发声机理不同，因此在波形上也存在着较大的差异。清音的时间波形呈现出随机噪声的特性，杂乱无章，样点间相似性较差，而浊音的时间波形呈现出一定的周期性，波形之间相似性较好[6]。

对于能量有限的语音信号x(n)，其自相关函数可定义为

(4)

如果x(n)是随机的或者周期性的离散语音信号，不是能量有限的，其自相关函数定义为

(5)

信号的自相关函数具有以下重要性质：

1)偶函数性质：r(k)=r(-k)；

2)|r(k)|≤|r(0)|，即零延迟的自相关函数值最大；

3)若x(n)为周期性信号，那么r(k)也是周期性信号，并且其周期与x(n)的周期相同。

与信号本身相比，自相关函数可以有效地抑制加性白噪声。因此利用自相关函数提取的周期具有较好的噪声稳定性。由于浊音信号具有准周期性，浊音信号的自相关函数在基音周期整数倍的位置上会出现峰值，而清音的自相关函数没有明显的峰值出现，因此检测是否有峰值可以判断清音或浊音。对于浊音信号，只要检测到峰值的位置，就可以估计出语音信号的基音周期值[7]。

为了提高自相关函数法检测基音周期的可靠性和计算效率，需要对原始的语音信号进行预处理：中心削波和三电平量化。中心削波法如式(6)所示。

(6)

式中CL为削波电平，一般取最大信号幅度的60%～70%。中心削波法处理能够有效减少倍周期和半周期估计错误。

为减少计算量，再进一步对信号y(n)进行三电平量化得到

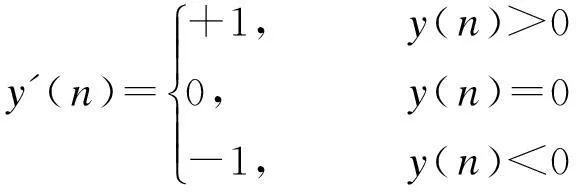
(7)

在基音周期检测中，用心削波信号y(n)与三电平信号y(n)的互相关来代替语音信号x(n)的自相关函数，即

(8)

式中N为语音帧的长度。式(8)所定义的自相关函数序列r(k)与式(5)中的自相关函数具有类似性质，即在基音周期整数倍的位置，r(k)具有峰值。

由r(k)定义类谐波积谱函数：

(9)

通常，可以取M=5。此外，为了保证在对r(k)进行n倍抽取时，不破坏r(nk)的准周期性，可以先对r(k)进行M倍内插，然后再计算类谐波积谱函数R(k)。

基于自相关的类谐波积谱法基音周期估计步骤如下：

(2)根据式(8)计算r(k)，并对其进行M倍内插。

(3)根据式(9)计算类谐波积谱函数R(k)。

(4)在[k1,k2]范围内找到R(k)最大值所对应的k0，即

R(k0)=max{R(k),k1≤k≤k2}

则k0即为该帧语音的基音周期。其中k1、k2分别为基音周期的上下限。

(5)如果R(k0)

图1为一段信噪比为SNR=3.2dB的浊音语音段的类谐波积谱函数。可以明显看出，在其基音周期处取得最大值(零点处除外)。该段语音由式(8)计算得到的相关函数值如图2所示。在图2中可以看到，除零点外，r(k)在三倍基音周期处取得最大值(零点处除外)，因此该段语音由r(k)估计的基音周期是错误的。

图1　类谐波积谱函数波形图

图2　由式(8)计算得到的相关函数值

3与自相关函数法比较

仿真实验所用的原始语音是普通话“妈妈，好吗，上马，骂人”，语音信号采样率为16kHz、量化字长16bit。选用截止频率为900Hz的低通滤波器进行预处理；采用汉明窗，窗宽度为600采样点。分别用自相关函数法和本文提出的基于自相关函数的类谐波积谱算法对语音信号进行基音周期提取，其结果如图3所示。

图3　原始语音信号的基音周期检测

图3为高信噪比情况下(未对原始语音另加噪声)使用传统自相关函数法和本文算法对该段语音进行基音检测的结果。图中横坐标为帧数，纵坐标为采样点数(对应基音周期)。图3a为连续无噪的语音信号“妈妈，好吗，上马，骂人”的波形图。图3b为自相关方法对原始语音信号进行基音周期检测的实验结果。从它们的基音轨迹可以看出，传统的相关函数进行基音周期检测，在多处出现明显的倍周期错误，这是由于受以共振峰为主的多种因素的影响，导致相关函数法除零点之外的第一最大峰值点并不是真实的基音点，因此检测结果并不理想。图3c为本文的类谐波积谱法对原始语音信号进行基音周期检测的实验结果。这种方法相较于相关函数法，克服了多处倍周期错误。本文算法对清浊音划分非常准确，检测所得的基音曲线光滑规整，很好地跟踪了基音周期的变化，并有效地修正了传统相关函数算法中的多处倍周期错误。

图4给出了在信噪比SNR=0dB的情况下，相关函数法和本文算法对该段语音进行基音检测的结果。由图4中的曲线对比可见，传统自相关函数法提取的基音轨迹出现了严重的不连续现象，检测效果不佳，容易出现半周期和倍周期的错误。而本文算法所给出的检测结果与无噪声条件下的检测结果大体保持一致，语音的基音曲线光滑规整，没有明显的倍周期和半周期错误，说明本文所提方法具有很好的噪声稳定性。

图4　信噪比SNR=0dB的加噪语音信号基音周期检测结果

4结论

以语音信号的基音检测为研究对象，提出了一种结合自相关函数法和谐波积谱的基音周期估计方法。用Matlab软件进行仿真实验，实验结果表明，这种新的基音周期检测方法在不同的信噪比情况下都具有很好的噪声稳定性，明显优于传统自相关法。

参考文献：

[1]Mousset Eric，Ainsworth William A，Fonollosa Jose A R.Acomparison of seceral recent methods of fundamental frequency and voicing decision estimation[C]//ICSLP 96.Phiadelphia，USA：IEEE，1996：1273-1276.

[2]徐敬德，常亮，崔慧娟，等.基于频域和时域结合的基音周期提取算法[J].清华大学学报：自然科学版，2012，52(3)：26-27.

[3]魏旋，党晓妍，崔慧娟，等.基于动态规划的低延时基音提取算法[J].清华大学学报:自然科学版，2008，48(10)：1586-1588.

[4]Kumar K，Jain J.Speech pitch shifting using complex continuous wavelet transform[C]//Annual IEEE India Conference.New Delhi，India，2006：1-4.

[5]易克初，田斌，付强.语音信号处理[M].北京：国防工业出版社，2000.

[6]李永宁.基于自相关的语音基音周期检测方法研究[J].福建电脑，2008(11)：92-93.

[7]何姣.带噪语音信号基音检测技术研究[D].成都：电子科技大学，2012.

(责任编辑：马金发)

Pitch Detection of Harmonic Product Spectrum-like Function

MEI Tiemin1,FU Tianjiao1，ZHU Xiangrong2

(1.Shenyang Ligong University,Shenyang 110159,China;2.Zibo Mintong Heating Co.,Ltd.,Zibo 255400,China)

Abstract：Pitch detection is an important researching topic in signal processing.One of the frequently used algorithms is based on autocorrelation function,estimation errors frequently occur for low signal-to-noise ratio (SNR) speech signals.To overcome such problems and motivated by the harmonic product spectrum (HPS) method,a novel pitch estimation method is proposed by defining an HPS-like function of the autocorrelation of speech signal.The novel method can not only overcome the shortcomings of HPS if one of the harmonics has zero amplitude,but also be more robust under low SNR.

Key words：pitch detection;autocorrelation;harmonic product spectrum-like function

中图分类号：TN912

文献标志码：A

文章编号：1003-1251(2016)02-0014-04

作者简介：梅铁民(1964—)，男，教授，博士，研究方向：信号处理。

收稿日期：2014-12-11